Verifying Volume Rendering Using Discretization Error Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mathematics Is a Gentleman's Art: Analysis and Synthesis in American College Geometry Teaching, 1790-1840 Amy K
Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 2000 Mathematics is a gentleman's art: Analysis and synthesis in American college geometry teaching, 1790-1840 Amy K. Ackerberg-Hastings Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Higher Education and Teaching Commons, History of Science, Technology, and Medicine Commons, and the Science and Mathematics Education Commons Recommended Citation Ackerberg-Hastings, Amy K., "Mathematics is a gentleman's art: Analysis and synthesis in American college geometry teaching, 1790-1840 " (2000). Retrospective Theses and Dissertations. 12669. https://lib.dr.iastate.edu/rtd/12669 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margwis, and improper alignment can adversely affect reproduction. in the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. -

Realistic Modeling and Rendering of Plant Ecosystems
Realistic modeling and rendering of plant ecosystems Oliver Deussen1 Pat Hanrahan2 Bernd Lintermann3 RadomÂõr MechÏ 4 Matt Pharr2 Przemyslaw Prusinkiewicz4 1 Otto-von-Guericke University of Magdeburg 2 Stanford University 3 The ZKM Center for Art and Media Karlsruhe 4 The University of Calgary Abstract grasslands, human-made environments, for instance parks and gar- dens, and intermediate environments, such as lands recolonized by Modeling and rendering of natural scenes with thousands of plants vegetation after forest ®res or logging. Models of these ecosystems poses a number of problems. The terrain must be modeled and plants have a wide range of existing and potential applications, including must be distributed throughout it in a realistic manner, re¯ecting the computer-assisted landscape and garden design, prediction and vi- interactions of plants with each other and with their environment. sualization of the effects of logging on the landscape, visualization Geometric models of individual plants, consistent with their po- of models of ecosystems for research and educational purposes, sitions within the ecosystem, must be synthesized to populate the and synthesis of scenes for computer animations, drive and ¯ight scene. The scene, which may consist of billions of primitives, must simulators, games, and computer art. be rendered ef®ciently while incorporating the subtleties of lighting Beautiful images of forests and meadows were created as early in a natural environment. as 1985 by Reeves and Blau [50] and featured in the computer We have developed a system built around a pipeline of tools that animation The Adventures of Andre and Wally B. [34]. Reeves and address these tasks. -

B.Casselman,Mathematical Illustrations,A Manual Of
1 0 0 setrgbcolor newpath 0 0 1 0 360 arc stroke newpath Preface 1 0 1 0 360 arc stroke This book will show how to use PostScript for producing mathematical graphics, at several levels of sophistication. It includes also some discussion of the mathematics involved in computer graphics as well as a few remarks about good style in mathematical illustration. To explain mathematics well often requires good illustrations, and computers in our age have changed drastically the potential of graphical output for this purpose. There are many aspects to this change. The most apparent is that computers allow one to produce graphics output of sheer volume never before imagined. A less obvious one is that they have made it possible for amateurs to produce their own illustrations of professional quality. Possible, but not easy, and certainly not as easy as it is to produce their own mathematical writing with Donald Knuth’s program TEX. In spite of the advances in technology over the past 50 years, it is still not a trivial matter to come up routinely with figures that show exactly what you want them to show, exactly where you want them to show it. This is to some extent inevitable—pictures at their best contain a lot of information, and almost by definition this means that they are capable of wide variety. It is surely not possible to come up with a really simple tool that will let you create easily all the graphics you want to create—the range of possibilities is just too large. -

The Table Lens: Merging Graphical and Symbolic Representations in an Interactive Focus+ Context Visualization for Tabular Information
HumanFac(orsinComputingSystems CHI’94 0 “Celebra/i//ghrferdepende)~cc” The Table Lens: Merging Graphical and Symbolic Representations in an Interactive Focus+ Context Visualization for Tabular Information Ramana Rao and Stuart K. Card Xerox Palo Alto Research Center 3333 Coyote Hill Road Palo Alto, CA 94304 Gao,carcM@parc. xerox.com ABSTRACT (at cell size of 100 by 15 pixels, 82dpi). The Table Lens can We present a new visualization, called the Table Lens, for comfortably manage about 30 times as many cells and can visualizing and making sense of large tables. The visual- display up to 100 times as many cells in support of many ization uses a focus+ccmtext (fisheye) technique that works tasks. The scale advantage is obtained by using a so-called effectively on tabular information because it allows display “focus+context” or “fisheye” technique. These techniques of crucial label information and multiple distal focal areas. allow interaction with large information structures by dynam- In addition, a graphical mapping scheme for depicting table ically distorting the spatial layout of the structure according to contents has been developed for the most widespread kind the varying interest levels of its parts. The design of the Table of tables, the cases-by-variables table. The Table Lens fuses Lens technique has been guided by the particular properties symbolic and gaphical representations into a single coherent and uses of tables. view that can be fluidly adjusted by the user. This fusion and A second contribution of our work is the merging of graphical interactivity enables an extremely rich and natural style of representations directly into the process of table visualization direct manipulation exploratory data analysis. -

Army Acquisition Workforce Dependency on E-Mail for Formal
ARMY ACQUISITION WORKFORCE DEPENDENCY ON E-MAIL FOR FORMAL WORK COORDINATION: FINDINGS AND OPPORTUNITIES FOR WORKFORCE PERFORMANCE IMPROVEMENT THROUGH E-MAIL-BASED SOCIAL NETWORK ANALYSIS KENNETH A. LORENTZEN May 2013 PUBLISHED BY THE DEFENSE ACQUISITION UNIVERSITY PRESS PROJECT ADVISOR: BOB SKERTIC CAPITAL AND NORTHEAST REGION, DAU THE SENIOR SERVICE COLLEGE FELLOWSHIP PROGRAM ABERDEEN PROVING GROUND, MD PAGE LEFT BLANK INTENTIONALLY .ARMY ACQUISITION WORKFORCE DEPENDENCY ON E-MAIL FOR FORMAL WORK COORDINATION: FINDINGS AND OPPORTUNITIES FOR WORKFORCE PERFORMANCE IMPROVEMENT THROUGH E-MAIL-BASED SOCIAL NETWORK ANALYSIS KENNETH A. LORENTZEN May 2013 PUBLISHED BY THE DEFENSE ACQUISITION UNIVERSITY PRESS PROJECT ADVISOR: BOB SKERTIC CAPITAL AND NORTHEAST REGION, DAU THE SENIOR SERVICE COLLEGE FELLOWSHIP PROGRAM ABERDEEN PROVING GROUND, MD PAGE LEFT BLANK INTENTIONALLY ii Table of Contents Table of Contents ............................................................................................................................ ii List of Figures ................................................................................................................................ vi Abstract ......................................................................................................................................... vii Chapter 1—Introduction ................................................................................................................. 1 Background and Motivation ................................................................................................. -

Semantic Foundation of Diagrammatic Modelling Languages
Universität Leipzig Fakultät für Mathematik und Informatik Institut für Informatik Johannisgasse 26 04103 Leipzig Semantic Foundation of Diagrammatic Modelling Languages Applying the Pictorial Turn to Conceptual Modelling Diplomarbeit im Studienfach Informatik vorgelegt von cand. inf. Alexander Heußner Leipzig, August 2007 betreuender Hochschullehrer: Prof. Dr. habil. Heinrich Herre Institut für Medizininformatik, Statistik und Epidemologie (I) Härtelstrasse 16–18 04107 Leipzig Abstract The following thesis investigates the applicability of the picto- rial turn to diagrammatic conceptual modelling languages. At its heart lies the question how the “semantic gap” between the for- mal semantics of diagrams and the meaning as intended by the modelling engineer can be bridged. To this end, a pragmatic ap- proach to the domain of diagrams will be followed, starting from pictures as the more general notion. The thesis consists of three parts: In part I, a basic model of cognition will be proposed that is based on the idea of conceptual spaces. Moreover, the most central no- tions of semiotics and semantics as required for the later inves- tigation and formalization of conceptual modelling will be intro- duced. This will allow for the formalization of pictures as semi- otic entities that have a strong cognitive foundation. Part II will try to approach diagrams with the help of a novel game-based F technique. A prototypical modelling attempt will reveal basic shortcomings regarding the underlying formal foundation. It will even become clear that these problems are common to all current conceptualizations of the diagram domain. To circumvent these difficulties, a simple axiomatic model will be proposed that allows to link the findings of part I on conceptual modelling and formal languages with the newly developed con- cept of «abstract logical diagrams». -

Geotime As an Adjunct Analysis Tool for Social Media Threat Analysis and Investigations for the Boston Police Department Offeror: Uncharted Software Inc
GeoTime as an Adjunct Analysis Tool for Social Media Threat Analysis and Investigations for the Boston Police Department Offeror: Uncharted Software Inc. 2 Berkeley St, Suite 600 Toronto ON M5A 4J5 Canada Business Type: Canadian Small Business Jurisdiction: Federally incorporated in Canada Date of Incorporation: October 8, 2001 Federal Tax Identification Number: 98-0691013 ATTN: Jenny Prosser, Contract Manager, [email protected] Subject: Acquiring Technology and Services of Social Media Threats for the Boston Police Department Uncharted Software Inc. (formerly Oculus Info Inc.) respectfully submits the following response to the Technology and Services of Social Media Threats RFP. Uncharted accepts all conditions and requirements contained in the RFP. Uncharted designs, develops and deploys innovative visual analytics systems and products for analysis and decision-making in complex information environments. Please direct any questions about this response to our point of contact for this response, Adeel Khamisa at 416-203-3003 x250 or [email protected]. Sincerely, Adeel Khamisa Law Enforcement Industry Manager, GeoTime® Uncharted Software Inc. [email protected] 416-203-3003 x250 416-708-6677 Company Proprietary Notice: This proposal includes data that shall not be disclosed outside the Government and shall not be duplicated, used, or disclosed – in whole or in part – for any purpose other than to evaluate this proposal. If, however, a contract is awarded to this offeror as a result of – or in connection with – the submission of this data, the Government shall have the right to duplicate, use, or disclose the data to the extent provided in the resulting contract. GeoTime as an Adjunct Analysis Tool for Social Media Threat Analysis and Investigations 1. -

On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle
On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle Agah D. Garnadi 31 December 2017 Department of Mathematics, Faculty of Mathematics and Natural Sciences, Bogor Agricultural University Jl. Meranti, Kampus IPB Darmaga, Bogor, 16680 Indonesia Abstract This note is addressed to solving biperiodic boundary value prob- lem of biharmonic equation in the unit rectangle. First, we describe the necessary tools, which is discrete Fourier transform for one di- mensional periodic sequence, and then extended the results to 2- dimensional biperiodic sequence. Next, we use the discrete Fourier transform 2-dimensional biperiodic sequence to solve discretization of the biperiodic boundary value problem of Biharmonic Equation. MSC: 15A09; 35K35; 41A15; 41A29; 94A12. Key words: Biharmonic equation, biperiodic boundary value problem, discrete Fourier transform, Partial differential equations, Interpola- tion. 1 Introduction This note is an extension of a work by Henrici [2] on fast solver for Poisson equation to biperiodic boundary value problem of biharmonic equation. This 1 note is organized as follows, in the first part we address the tools needed to solve the problem, i.e. introducing discrete Fourier transform (DFT) follows Henrici's work [2]. The second part, we apply the tools already described in the first part to solve discretization of biperiodic boundary value problem of biharmonic equation in the unit rectangle. The need to solve discretization of biharmonic equation is motivated by its occurence in some applications such as elasticity and fluid flows [1, 4], and recently in image inpainting [3]. Note that the work of Henrici [2] on fast solver for biperiodic Poisson equation can be seen as solving harmonic inpainting. -

Visualization in Multiobjective Optimization
Final version Visualization in Multiobjective Optimization Bogdan Filipič Tea Tušar Tutorial slides are available at CEC Tutorial, Donostia - San Sebastián, June 5, 2017 http://dis.ijs.si/tea/research.htm Computational Intelligence Group Department of Intelligent Systems Jožef Stefan Institute Ljubljana, Slovenia 2 Contents Introduction A taxonomy of visualization methods Visualizing single approximation sets Introduction Visualizing repeated approximation sets Summary References 3 Introduction Introduction Multiobjective optimization problem Visualization in multiobjective optimization Minimize Useful for different purposes [14] f: X ! F • Analysis of solutions and solution sets f:(x ;:::; x ) 7! (f (x ;:::; x );:::; f (x ;:::; x )) 1 n 1 1 n m 1 n • Decision support in interactive optimization • Analysis of algorithm performance • X is an n-dimensional decision space ⊆ Rm ≥ • F is an m-dimensional objective space (m 2) Visualizing solution sets in the decision space • Problem-specific ! Conflicting objectives a set of optimal solutions • If X ⊆ Rm, any method for visualizing multidimensional • Pareto set in the decision space solutions can be used • Pareto front in the objective space • Not the focus of this tutorial 4 5 Introduction Introduction Visualization can be hard even in 2-D Stochastic optimization algorithms Visualizing solution sets in the objective space • Single run ! single approximation set • Interested in sets of mutually nondominated solutions called ! approximation sets • Multiple runs multiple approximation sets • Different -

Inviwo — a Visualization System with Usage Abstraction Levels
IEEE TRANSACTIONS ON VISUALIZATION AND COMPUTER GRAPHICS, VOL X, NO. Y, MAY 2019 1 Inviwo — A Visualization System with Usage Abstraction Levels Daniel Jonsson,¨ Peter Steneteg, Erik Sunden,´ Rickard Englund, Sathish Kottravel, Martin Falk, Member, IEEE, Anders Ynnerman, Ingrid Hotz, and Timo Ropinski Member, IEEE, Abstract—The complexity of today’s visualization applications demands specific visualization systems tailored for the development of these applications. Frequently, such systems utilize levels of abstraction to improve the application development process, for instance by providing a data flow network editor. Unfortunately, these abstractions result in several issues, which need to be circumvented through an abstraction-centered system design. Often, a high level of abstraction hides low level details, which makes it difficult to directly access the underlying computing platform, which would be important to achieve an optimal performance. Therefore, we propose a layer structure developed for modern and sustainable visualization systems allowing developers to interact with all contained abstraction levels. We refer to this interaction capabilities as usage abstraction levels, since we target application developers with various levels of experience. We formulate the requirements for such a system, derive the desired architecture, and present how the concepts have been exemplary realized within the Inviwo visualization system. Furthermore, we address several specific challenges that arise during the realization of such a layered architecture, such as communication between different computing platforms, performance centered encapsulation, as well as layer-independent development by supporting cross layer documentation and debugging capabilities. Index Terms—Visualization systems, data visualization, visual analytics, data analysis, computer graphics, image processing. F 1 INTRODUCTION The field of visualization is maturing, and a shift can be employing different layers of abstraction. -

A Process for Digitizing and Simulating Biologically Realistic Oligocellular Networks Demonstrated for the Neuro-Glio-Vascular Ensemble Edited By: Yu-Guo Yu, Jay S
fnins-12-00664 September 27, 2018 Time: 15:25 # 1 METHODS published: 25 September 2018 doi: 10.3389/fnins.2018.00664 A Process for Digitizing and Simulating Biologically Realistic Oligocellular Networks Demonstrated for the Neuro-Glio-Vascular Ensemble Edited by: Yu-Guo Yu, Jay S. Coggan1 †, Corrado Calì2 †, Daniel Keller1, Marco Agus3,4, Daniya Boges2, Fudan University, China * * Marwan Abdellah1, Kalpana Kare2, Heikki Lehväslaiho2,5, Stefan Eilemann1, Reviewed by: Renaud Blaise Jolivet6,7, Markus Hadwiger3, Henry Markram1, Felix Schürmann1 and Clare Howarth, Pierre J. Magistretti2 University of Sheffield, United Kingdom 1 Blue Brain Project, École Polytechnique Fédérale de Lausanne (EPFL), Geneva, Switzerland, 2 Biological and Environmental Ying Wu, Sciences and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 3 Visual Xi’an Jiaotong University, China Computing Center, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 4 CRS4, Center of Research *Correspondence: and Advanced Studies in Sardinia, Visual Computing, Pula, Italy, 5 CSC – IT Center for Science, Espoo, Finland, Jay S. Coggan 6 Département de Physique Nucléaire et Corpusculaire, University of Geneva, Geneva, Switzerland, 7 The European jay.coggan@epfl.ch; Organization for Nuclear Research, Geneva, Switzerland [email protected] Corrado Calì [email protected]; One will not understand the brain without an integrated exploration of structure and [email protected] function, these attributes being two sides of the same coin: together they form the †These authors share first authorship currency of biological computation. Accordingly, biologically realistic models require the re-creation of the architecture of the cellular components in which biochemical reactions Specialty section: This article was submitted to are contained. -
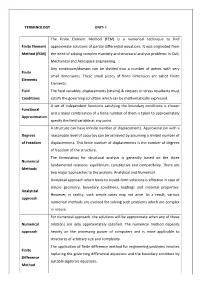
TERMINOLOGY UNIT- I Finite Element Method (FEM)
TERMINOLOGY UNIT- I The Finite Element Method (FEM) is a numerical technique to find Finite Element approximate solutions of partial differential equations. It was originated from Method (FEM) the need of solving complex elasticity and structural analysis problems in Civil, Mechanical and Aerospace engineering. Any continuum/domain can be divided into a number of pieces with very Finite small dimensions. These small pieces of finite dimension are called Finite Elements Elements. Field The field variables, displacements (strains) & stresses or stress resultants must Conditions satisfy the governing condition which can be mathematically expressed. A set of independent functions satisfying the boundary conditions is chosen Functional and a linear combination of a finite number of them is taken to approximately Approximation specify the field variable at any point. A structure can have infinite number of displacements. Approximation with a Degrees reasonable level of accuracy can be achieved by assuming a limited number of of Freedom displacements. This finite number of displacements is the number of degrees of freedom of the structure. The formulation for structural analysis is generally based on the three Numerical fundamental relations: equilibrium, constitutive and compatibility. There are Methods two major approaches to the analysis: Analytical and Numerical. Analytical approach which leads to closed-form solutions is effective in case of simple geometry, boundary conditions, loadings and material properties. Analytical However, in reality, such simple cases may not arise. As a result, various approach numerical methods are evolved for solving such problems which are complex in nature. For numerical approach, the solutions will be approximate when any of these Numerical relations are only approximately satisfied.