Computing Multiparameter Persistent Homology Through a Discrete Morse-Based Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Accessories 1
MOTOMAN Accessories 1 Accessories Program www.yaskawa.eu.com Masters of Robotics, Motion and Control Contents Accessories Cable Retraction System for Teach Pendants ..................................................... 5 Media Packages suitable for all Applications ....................................................... 7 Robot Pedestals and Robot Base Plates for MOTOMAN Robots ............................................................ 9 External Drive Axes Packages for MOTOMAN Robots with DX200 Controller ....................... 17 Touch Sensor Search Sensor with Welding Wire .......................................... 21 MotoFit Force Control Assembly Tool ................................................ 23 YASKAWA Vision System Camera & Software MotoSight2D .......................................... 25 Fieldbus Systems .................................................................. 27 4 Accessories MOTOMAN Accessories 5 Cable Retraction System for Teach Pendants The automatic YASKAWA cable retraction system has been specially developed for the connecting cables of industrial robot teach pendants. This system is used to improve work safety in the production area and is a recognized accident prevention measure. The stable housing is made of impactresistant plastic, while the mounting bracket is made of steel plate, enabling alignment of the retraction system housing in the direction in which the cable is pulled out. The cable deflection pulley is fitted with a spring element for cable retraction. Additionally, a releas- able cable -

IT's a WINNER! Refl Ecting All That's Great About British Dinghy Sailing
ALeXAnDRA PALACe, LOnDOn 3-4 March 2012 IT'S A WINNER! Refl ecting all that's great about British dinghy sailing 1647 DS Guide (52).indd 1 24/01/2012 11:45 Y&Y AD_20_01-12_PDF.pdf 23/1/12 10:50:21 C M Y CM MY CY CMY K The latest evolution in Sailing Hikepant Technology. Silicon Liquid Seam: strongest, lightest & most flexible seams. D3O Technology: highest performance shock absorption, impact protection solutions. Untitled-12 1 23/01/2012 11:28 CONTENTS SHOW ATTRACTIONS 04 Talks, seminars, plus how to get to the show and where to eat – all you need to make the most out of your visit AN OLYMPICS AT HOME 10 Andy Rice speaks to Stephen ‘Sparky’ Parks about the plus and minus points for Britain's sailing team as they prepare for an Olympic Games on home waters SAIL FOR GOLD 17 How your club can get involved in celebrating the 2012 Olympics SHOW SHOPPING 19 A range of the kit and equipment on display photo: rya* photo: CLubS 23 Whether you are looking for your first club, are moving to another part of the country, or looking for a championship venue, there are plenty to choose WELCOME SHOW MAP enjoy what’s great about British dinghy sailing 26 Floor plans plus an A-Z of exhibitors at the 2012 RYA Volvo Dinghy Show SCHOOLS he RYA Volvo Dinghy Show The show features a host of exhibitors from 29 Places to learn, or improve returns for another year to the the latest hi-tech dinghies for the fast and your skills historical Alexandra Palace furious to the more traditional (and stable!) in London. -

STILTS - Starlink Tables Infrastructure Library Tool Set
STILTS - Starlink Tables Infrastructure Library Tool Set Version 3.4-1 Starlink User Note256 Mark Taylor 10 June 2021 Abstract STILTS is a set of command-line tools for processing tabular data. It has been designed for, but is not restricted to, use on astronomical data such as source catalogues. It contains both generic (format-independent) table processing tools and tools for processing VOTable documents. Facilities offered include crossmatching, format conversion, format validation, column calculation and rearrangement, row selection, sorting, plotting, statistical calculations and metadata display. Calculations on cell data can be performed using a powerful and extensible expression language. The package is written in pure Java and based on STIL, the Starlink Tables Infrastructure Library. This gives it high portability, support for many data formats (including FITS, VOTable, text-based formats and SQL databases), extensibility and scalability. Where possible the tools are written to accept streamed data so the size of tables which can be processed is not limited by available memory. As well as the tutorial and reference information in this document, detailed on-line help is available from the tools themselves. The STILTS application is available under the GNU General Public License (GPL) though most parts of the library code may alternatively be used under the GNU Lesser General Public License (LGPL). Contents Abstract............................................................................................................................................ -

Dinghy Schedule/Resultsана2004
12/16/2014 Dinghy Schedule/Results 2004 ABOUT US RACING MEMBERS & SERVICES INSTRUCTOR SERVICES PROGRAMS SAILOR DEVELOPMENT THE STORE LOGIN Home > Racing > Racing Schedules/Results Dinghy Schedule/Results 2004 JANUARY 2004 Date Event Venue Classes January Rolex Miami Olympic Classes Regatta US Sailing Centre, Miami Olympic Classes 26 30 FEBRUARY 2004 Date Event Venue Classes February US Sailing Centre, Jensen Club 420, Laser, Club 420 Midwinters 14 15 Beach, Florida Byte February Clearwater Yacht Club, Laser Midwinters East Laser, Radial 26 29 Florida MARCH 2004 Date Event Venue Classes Thank you to our Premier Sponsors: March Mission Bay Yacht Club, Laser Midwinters West Laser, Radial 19 21 California APRIL 2004 Date Event Venue Classes April Laser Radial Open & Women's World Royal Queensland Yacht Laser Radial 1 8 Championships Squadron, Australia April Laser Radial Youth World Royal Queensland Yacht Laser Radial Check out all of our sponsors 10 17 Championships Squadron, Australia MAY 2004 Date Event Venue Classes May Frenchman's Bay Yacht Optimist, Laser, Unistrut Central Mother’s Day Regatta 8 9 Club Radial, Byte Montreal May High Performance Skiff Camp Contact: Skiffs 8 9 Tyler Bjorn [email protected] May Laser World Championships Bitez, Turkey Laser 10 19 Europe, Laser, Radial, Laser 2, May Lilac Festival Byte, 29er, Club 15 16 Royal Hamilton Yacht Club 420, Star, Yngling, Notice of Race Finn, 470, 49er, Martin 16, Optimist Queensway Audi Icebreakers & Gold Cup #1 Optimist, Laser, Radial, Byte, Laser Notice -

Vyc Yardsticks
Yachting Victoria Inc ABN 26 176 852 642 2 / 77 Beach Road SANDRINGHAM VIC 3191 Tel 03 9597 0066 Fax 03 9598 7384 YACHTING VICTORIA YARDSTICKS - 2013-14 Date: 1st Oct 2013 Version: 1.0 INTRODUCTION These yardsticks are prepared to provide the fairest possible calculation of results for mixed fleet racing. New and modified classes appear every year and it is important to gather information and review results as quickly as possible. For dinghy classes there have been no changes to the original Yardsticks published for the 2013/14 season, as results for review have not been forthcoming. In the absence of race results data for dinghy classes and new internationally sourced classes, where there is yardstick data from overseas available, a comparison is made with other international classes to derive an equivalent Yachting Victoria yardstick value. This is explained further down in this document. Fortunately for catamaran classes, there has been significant work done by the Kurnell Catamaran Club in reviewing various catamaran ratings, as well as validating the ratings against the international SCHRS system. This work has now been incorporated into the YV yardsticks for catamaran classes. Much appreciation goes to KCC for this good work. Catamaran yardsticks are now contained in a separate document: “YV - Cat Yardsticks13_14 v1.0” USE OF THE YV YARDSTICKS A club which intends to run a race or event under the Yachting Victoria Yardstick system should include in the Notice of Race and in the Sailing Instructions clauses based on the following: 1 The version of the YV Yardstick System that is to be used in calculating the mixed class fleet racing results. -

UK Byte Class Association Byte Spring Training Event Inside This
www.byteclass.org.uk Autumn 2012 No 48 UK Byte Class Association Inside this issue Page Byte Spring Training Event 1 Ian Bruce Sells Byte Rights 2 Minutes of AGM 3 Byte Open at West Oxfordshire Sailing Club 6 Byte Open at Cardiff Yacht Club 7 Byte Open at Combs SC 8 Byte Nationals at Brixham 9 Byte Open Meeting at Weston Sailing Club 10 Byte Open at Haversham SC 10 Byte Spring Training Event 20th-21st April 2013 Come and join a Spring Break at Rutland SC. Enjoy fantastic training with hints and tips on how to get maxi- mum enjoyment and speed out of your Byte. Our last training weekend at Rutland was very successful so we are going to run it again. Rutland is easily accessible from the North and South via the M1 or A1 and the area has lots for partners or families to do – cycle hire, walking, sailing tuition, boat trips etc. Have a look at www.rutlandsc.co.uk and also at www.rutlandwater.org.uk This training is for everyone who sails a Byte. Whether you think you do it badly or well - you will be amongst friends! Coaching will include some time on land looking at how to set up the boat for different wind conditions and some classroom time looking at video clips of good (and bad) techniques. The vertically chal- lenged amongst us have learnt new techniques for righting a capsized Byte and will get a chance to demon- strate. On Saturday we will start at a civilised 10am. -
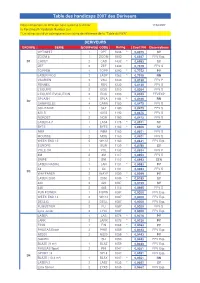
Table Des Handicaps 2007 Des Dériveurs
Table des handicaps 2007 des Dériveurs Nous remercions le RYA qui nous autorise à utiliser 17/04/2007 la Porstmouth Yardstick Number List. * Le rating suivi d'un astérique est un rating de référence de la "Table du RYA" DERIVEURS GROUPE SERIE EQUIPAGE CODE Rating Coeff PN Observations OPTIMIST 1 OPT 1646 * 0,6075 SY ZOOM 8 1 ZOOM 1500 0,6667 FFV Exp. D1 CADET 2 CAD 1432 * 0,6983 SY ZEF 2 ZEF 1330 0,7519 FFV S TOPPER 1 TOPP 1290 * 0,7752 PY LASER PICO 2 LASP 1263 * 0,7918 RN VAURIEN 2 VAU 1230 0,8130 FFV P FENNEC 2 FEN 1230 0,8130 FFV S L'EQUIPE 2 EQU 1210 0,8264 FFV S L'EQUIPE EVOLUTION 2 EQU 1200 0,8333 FFVEXP SPLASH 1 SPLA 1184 * 0,8446 RN D2 CARAVELLE 4 CARA 1180 0,8475 FFV S SOLITAIRE 1 SLT 1180 0,8475 FFV S 420 S 1 420S 1180 0,8475 FFV S NORDET 2 NOR 1180 0,8475 FFV S LASER 4.7 1 LAS4 1175 * 0,8511 SY BYTE 1 BYTE 1162 * 0,8606 SY R9M 1 R9M 1160 0,8621 FFV S MOUSSE 2 MOU 1160 0,8621 FFV S WEEK END 12 5 WK12 1160 0,8621 FFV Exp. EUROPE 1 EUR 1139 * 0,8780 SY YOLE OK 1 YOL 1132 0,8834 FFV P 4M 2 4M 1117 0,8953 FFV S SNIPE 2 SNI 1112 0,8993 STN LASER RADIAL 1 LAR 1101 * 0,9083 PY X4 1 X4 1101 0,9083 FFV S D3 WAYFARER 2 WAYF 1099 * 0,9099 PY LASER 2000 2 2000 1089 * 0,9183 SY 420 2 420 1087 0,9199 SY 445 2 445 1113 0,8985 FFV S FUN POWER 1 FUPW 1087 0,9200 FFV Exp. -

2021 Boat Parking Fees
2021 Boat Parking Fees Fee payable: boat length x beam rounded to closest sq. m. Main compound: £9 per sq. m. Minster compound: £4.5 per sq. m. COST PER YEAR: Class Length Beam m2 MAIN compound MINSTER compound 29er 4.45 1.77 8 £72 £36 29erxx 4.45 1.77 8 £72 £36 420 4.2 1.71 7 £63 £32 470 4.7 1.68 8 £72 £36 49er 4.99 2.9 14 £126 £63 505 5.05 1.88 9 £81 £41 Access 2.3 2.3 1.25 3 £27 £14 Access 303 3.03 1.35 4 £36 £18 Albacore 4.57 1.53 7 £63 £32 B14 4.25 3.05 13 £117 £59 Blaze 4.2 2.48 10 £90 £45 Bobbin 2.74 1.27 3 £27 £14 Boss 4.9 2 10 £90 £45 Bosun 4.27 1.68 7 £63 £32 Buzz 4.2 1.92 8 £72 £36 Byte 3.65 1.3 5 £45 £23 Cadet 3.22 1.27 4 £36 £18 Catapult 5 2.25 11 £99 £50 Challenger Tri 4.57 3.5 16 £144 £72 Cherub 3.7 1.8 7 £63 £32 Comet 3.45 1.37 5 £45 £23 Comet Duo 3.57 1.52 5 £45 £23 Comet Mino 3.45 1.37 5 £45 £23 Comet Race 4.27 1.63 7 £63 £32 Comet Trio 4.6 1.83 8 £72 £36 Comet Versa 3.96 1.65 7 £63 £32 Comet XTRA 3.45 1.37 5 £45 £23 Comet Zero 3.45 1.42 5 £45 £23 Contender 4.87 1.5 7 £63 £32 Cruz 4.58 1.82 8 £72 £36 Dart 15 4.54 2.13 10 £90 £45 Dart 16 4.8 2.3 11 £99 £50 Dart 18 5.5 2.29 13 £117 £59 Dart Hawk 5.5 2.6 14 £126 £63 Enterprise 4.04 1.62 7 £63 £32 Escape 12 3.89 1.52 6 £54 £27 Escape Captiva 3.6 1.6 6 £54 £27 Escape Mango 2.9 1.2 3 £27 £14 Escape Playcat 4.8 2.1 10 £90 £45 Escape Rumba 3.9 1.6 6 £54 £27 Escape Solsa 2.9 1.2 3 £27 £14 Europe 3.38 1.41 5 £45 £23 F18 5.52 2.6 14 £126 £63 Finn 4.5 1.5 7 £63 £32 Fireball 4.93 1.37 7 £63 £32 Firefly 3.66 1.42 5 £45 £23 Flash 3.55 1.3 5 £45 £23 Flying Fifteen 6.1 1.54 9 £81 £41 -

Centerboard Classes NAPY D-PN Wind HC
Centerboard Classes NAPY D-PN Wind HC For Handicap Range Code 0-1 2-3 4 5-9 14 (Int.) 14 85.3 86.9 85.4 84.2 84.1 29er 29 84.5 (85.8) 84.7 83.9 (78.9) 405 (Int.) 405 89.9 (89.2) 420 (Int. or Club) 420 97.6 103.4 100.0 95.0 90.8 470 (Int.) 470 86.3 91.4 88.4 85.0 82.1 49er (Int.) 49 68.2 69.6 505 (Int.) 505 79.8 82.1 80.9 79.6 78.0 A Scow A-SC 61.3 [63.2] 62.0 [56.0] Akroyd AKR 99.3 (97.7) 99.4 [102.8] Albacore (15') ALBA 90.3 94.5 92.5 88.7 85.8 Alpha ALPH 110.4 (105.5) 110.3 110.3 Alpha One ALPHO 89.5 90.3 90.0 [90.5] Alpha Pro ALPRO (97.3) (98.3) American 14.6 AM-146 96.1 96.5 American 16 AM-16 103.6 (110.2) 105.0 American 18 AM-18 [102.0] Apollo C/B (15'9") APOL 92.4 96.6 94.4 (90.0) (89.1) Aqua Finn AQFN 106.3 106.4 Arrow 15 ARO15 (96.7) (96.4) B14 B14 (81.0) (83.9) Bandit (Canadian) BNDT 98.2 (100.2) Bandit 15 BND15 97.9 100.7 98.8 96.7 [96.7] Bandit 17 BND17 (97.0) [101.6] (99.5) Banshee BNSH 93.7 95.9 94.5 92.5 [90.6] Barnegat 17 BG-17 100.3 100.9 Barnegat Bay Sneakbox B16F 110.6 110.5 [107.4] Barracuda BAR (102.0) (100.0) Beetle Cat (12'4", Cat Rig) BEE-C 120.6 (121.7) 119.5 118.8 Blue Jay BJ 108.6 110.1 109.5 107.2 (106.7) Bombardier 4.8 BOM4.8 94.9 [97.1] 96.1 Bonito BNTO 122.3 (128.5) (122.5) Boss w/spi BOS 74.5 75.1 Buccaneer 18' spi (SWN18) BCN 86.9 89.2 87.0 86.3 85.4 Butterfly BUT 108.3 110.1 109.4 106.9 106.7 Buzz BUZ 80.5 81.4 Byte BYTE 97.4 97.7 97.4 96.3 [95.3] Byte CII BYTE2 (91.4) [91.7] [91.6] [90.4] [89.6] C Scow C-SC 79.1 81.4 80.1 78.1 77.6 Canoe (Int.) I-CAN 79.1 [81.6] 79.4 (79.0) Canoe 4 Mtr 4-CAN 121.0 121.6 -

Pursuit Race Start Order Times Great Lakes 2020.Xlsx
Starcross Steamer 19th January 2020 Provisional Pursuit Race Start Times Based on Great Lakes Handicap 2019-20 Race Length 02:30 PN of Slowest Class 1390 Start Time 12:00 Minutes Nominal SailJuice After Start Class Number Start Time Cadet 1435 No Start No Start Topper 4.2 1391 No Start No Start Mirror 1390 00:00 12:00 Topper 1363 00:03 12:03 RS Tera Pro 1359 00:03 12:03 Heron 1345 00:05 12:05 Laser Pico 1330 00:06 12:06 RS Feva S 1280 00:12 12:12 Otter 1275 00:12 12:12 Fleetwind 1268 00:13 12:13 Signet 1265 00:13 12:13 Topaz Uno 1251 00:15 12:15 Comet Zero 1250 00:15 12:15 Vagabond 1248 00:15 12:15 RS Feva XL 1240 00:16 12:16 2.4m 1230 00:17 12:17 Sunfish 1229 00:17 12:17 RS Zest 1228 00:17 12:17 Splash 1220 00:18 12:18 Devon Yawl 1219 00:18 12:18 Laser 4.7 1210 00:19 12:19 Comet 1207 00:20 12:20 YW Dayboat 1200 00:21 12:21 Bosun 1198 00:21 12:21 Miracle 1194 00:21 12:21 Comet Mino 1193 00:21 12:21 Pacer 1193 00:21 12:21 Byte 1190 00:22 12:22 Firefly 1190 00:22 12:22 Topaz Duo 1190 00:22 12:22 Wanderer 1190 00:22 12:22 Topaz Vibe 1185 00:22 12:22 Comet Duo 1178 00:23 12:23 Byte CI 1177 00:23 12:23 Topaz Magno 1175 00:23 12:23 Lightning 368 1167 00:24 12:24 Comet Versa 1165 00:24 12:24 British Moth 1155 00:25 12:25 Streaker 1155 00:25 12:25 Solo 1152 00:26 12:26 Enterprise 1151 00:26 12:26 Laser Radial 1150 00:26 12:26 Europe 1141 00:27 12:27 Vaurien 1140 00:27 12:27 Yeoman 1140 00:27 12:27 Byte CII 1138 00:27 12:27 RS Aero 5 1136 00:27 12:27 GP 14 1130 00:28 12:28 RS Quest 1130 00:28 12:28 Graduate 1129 00:28 12:28 RS Vision 1128 00:28 -

TOPCAT - Tool for Operations on Catalogues and Tables
TOPCAT - Tool for OPerations on Catalogues And Tables Version 4.8-1 Starlink User Note253 Mark Taylor 10 June 2021 Abstract TOPCAT is an interactive graphical viewer and editor for tabular data. It has been designed for use with astronomical tables such as object catalogues, but is not restricted to astronomical applications. It understands a number of different astronomically important formats, and more formats can be added. It is designed to cope well with large tables; a million rows by a hundred columns should not present a problem even with modest memory and CPU resources. It offers a variety of ways to view and analyse the data, including a browser for the cell data themselves, viewers for information about table and column metadata, tools for joining tables using flexible matching algorithms, and extensive 2- and 3-d visualisation facilities. Using a powerful and extensible Java-based expression language new columns can be defined and row subsets selected for separate analysis. Selecting a row can be configured to trigger an action, for instance displaying an image of the catalogue object in an external viewer. Table data and metadata can be edited and the resulting modified table can be written out in a wide range of output formats. A number of options are provided for loading data from external sources, including Virtual Observatory (VO) services, thus providing a gateway to many remote archives of astronomical data. It can also interoperate with other desktop tools using the SAMP protocol. TOPCAT is written in pure Java and is available under the GNU General Public Licence. -

Development of the Virtual Sailing Dinghy Simulator
DEVELOPMENT OF THE VIRTUAL SAILING DINGHY SIMULATOR Norman R Saunders, Department of Pharmacology, University of Melbourne, Parkville, Victoria 3010, Australia. [email protected] Frank D Bethwaite, Bethwaite Design Pty Ltd, 2 Waine Street Harbord NSW 2096. [email protected]. Mark D Habgood, Department of Pharmacology, University of Melbourne, Parkville, Victoria 3010, Australia. [email protected] Jonathon Binns, Australian Maritime College, Locked Bag 1-357, Launceston, Tasmania, 7250, Australia. [email protected] ABSTRACT Virtual Sailing dinghy simulators (VS1 and VS2) have been developed from a prototype devised at the University of Tasmania, which in turn stemmed from mechanical simulators built at the University of Southampton in the 1980s. The VS2 consists of a Laser or Byte hull mounted on rollers and a steel frame. Computer controlled pneumatic rams provide for roll and tiller “feel” (eg weather helm). Controls for steering and sheeting are as in the normally rigged dinghy. The sailor is in a loop between the output side of the computer which controls the simulator and the input to the computer which measures the response of the sailor (hiking, steering and sheeting) on the simulator. The sailor views a computer screen which provides an image of where the dinghy is sailing and data on wind direction, gusts, position on race course. Software options provide for a wide range of variables: eg dinghy type, wind strength and direction, gusts, race conditions. The VS2 has a wide range of applications including teaching beginners and fast-tracking their early skill development, simulator racing and physiological measurements on elite sailors.