DOCSLIB.ORG

Unit 8 Taylor9$ Theorem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Unit 8 Taylor9$ Theorem UNIT 8 TAYLOR9$ THEOREM Structure 8.1 Introduction 5 Objectives 8.2 Taylor's The~rem 5 Taylor's Theorem for Functions of One Variable Taylor's Theorem for Functions of Two Variables 8.3 Maxima and Minima 15 . LocalExtrema Second Derivative Test for Local Extrema 8.4 Lagrange's Multipliers 8.5 Summary 8.6 Solutions and Answers 8.1 INTRODUCTION In this unit we state, without proof, Taylor's Theorem (about approximating a function by polynomials) for real-valued functions of several variables. This theorem is the principal tool for finding out the points of relative maxima and minima for these functions. We also discuss briefly Lagrange's method of multipliers, which enables us to locate the stationary points when the variables are not free but are subject to some additional conditions. In this unit we will be dealing with functions of two variables. Even though the results are true for any number of variables, their proof involves techniques which are not easy to understand at this level. So, for the sake of simplicity, we confine our attention to the two- variable case. We start our discussion with the one variable case. Objectives After studying this unit, you should be able to find the Taylor polynomials for functions of one or two variables, ., state and apply Taylor's theorem for functions of one and two variables, I I locate the stationary points of functions, use the second derivative test to find the nature of stationary points, use the technique of Lagrange's multipliers in locating the stationary points of functions of two variables. , 8.2 TAYLOR'S THEOREM In the calculus course you have seen (Unit 6) that if we know the values of a function of one variable and its derivatives at 0, then we can find an expression for the value of the function at a nearby point. We can derive a similar expression for functions of two variables using partial derivatives. This expression was first derived by Brook Taylor, an English mathematician of the eighteenth century. We shall first discuss Taylor's theorem for functions of a single variable. Taylor (1685-1731) 8.2.1 Taylor's Theorem for Functions of One Variable You will agree when we say that polynomials are by far the simplest functions in calculus. We can evaluate the value of a polynomial at a point by using the four basic operations of addition, multiplication, subtraction and division. However, the situation in the case of functions like ex- lnx, sinx, etc., is not so simple. These functions occur so frequently in all branches of mathematics, that approximate values of these fun&ns have been tabulated I ~pplicationsof Partial ' extensively. The main tool for this purpose has been to find polynomials which approximate Derivatives these functions in a neighbourhood of the point under consideration. You are already familiar with Lagrange's mean value theorem. This theorem states that if f(x) is differentiable in some neighbourhood N of the point x,, then we have for all x such that [x,;x] or [x, x,] is contained in N. Here 5 is a point lying between x, and X. Iff is twice differentiable in N, then, again applying mean value theorem to the function f, we can go a step further and write - 1 f(x) = f(x,) + (x-x,) f (x,)+ 5 f' (6) (x-xo)l , where 6 is some point in N lying between x, and x. Thus, the constant polynomial f(x,) approximates f(x) in N in the first case, while the polynomial f(x,) + (x-x,) f (x,)approximates f(x) in N in the second case. The difference between the actual value and the approximated value is called the error term. 1 The error term in the first case is f (5) (x-x,), and in the second case it is - f" (6) (x-xJ2. We 2 can estimate these error terms iff and f" are bounded. Taylor's theorem tells us that if a function f(x) has derivatives of all orders upto n+l in a neighbourhood of x,, then we can find polynomials P,(x), ...... Pn (x) of degree 0, ...... n, respectively, such that the error term f(x) - P,(x) is a polynomial of degree less than or equal to r+l. Note that here we consider the polynomial 0 also as a polynomial of degree zero, which is not the usual practice. We have done this for the sake of uniformity of expression. In order to state the precise result, we 1 start with the following definition. I ' Definition 1 : Let f(x) be a real-valued function having derivatives upto order n 2 1 at the point x, . A polynomial P(x) is said to be the rth Taylor polynomial of f(x) at x,, if i) the degree of P(x) lr, r I n ii) P(j)(x,) = f(j) (q)for 0 lj lr, where Po)(x,) = P(x,) and fro, (x,) = f(x,). Recall that a polynomial P(x) is an expression that can be written as where c,, c,, ....... cn are real numbers. Apart from these there are expressions like P(x) = c, + c, (x-x,) + ...... + c, (x-x,)" . ... (2) where x,, c,, c,, .... are real numbers and x, # 0, which are also called polynomials. You can easily see that (2) can be rewritten in the form (1) by expanding the powers (x-x,)~, .... (x-x,)". We also call the expression in (1) a polynomial it zero and.that in (2), a polynomial at x,. Now we state and prove a theorem which tells us that Taylor plynomials of a given function are unique. It also tells us how to find out the Taylor polynomials of a given function. Theorem 1 : Let %. .... a, be any r + 1 real numbers. Then there exists a unique polynomial P(x) such that i) The degree of P(x) Ir ii) Pc~)(x,)=a~,OSjIr, where x, is any fixed real number. Taylor's Theorem 1 Moreover. P(x) = C,'a, -(x-xJrn. m! I Proof :We can write a polynomial at x, as where bo . ....., b, are real numbers. Now we have to determine b,, ....., br such that P")(x,) = a, for 0 I jI r. If we differentiate the expression in (3) jtimes, then we get , r Fj)(x) =zk (k- 1) .... (k -j + 1,) 4, (x-x~)~-~,1 I j 5 r, k=j and therefore, Thus. Also, Hence, PC J ) (x,) "j= j! forOljlr Substituting for bj s in (3) , we get Note that the polynomial P(x) will be of degree r if and only if a, # 0. Now by (4) we can conclude that the polynomial is unique. The following corollary of Theorem 1 tells us how to find the Taylor polynomials of a given function. Corollary 1 :If f(x) is a real-valued function having derivatives of all orders upto n (n 2 1)' then the mh Taylor polynomial of f(x) at x, is given by Proof : Let us take a, = fi) (x,), 0 5 k .5 m, in Theorem 1. Then the mh Taylor polynomial off, if it exists; must be in the form of Equation (5). Thus, \ The above discussion shows that the Taylor polynomials of a given function can be found step by step using. the relation 1 MOrebver, if P,,,(x) is the mb Taylor polynomial of f(x) at x, ,then you can check that the derivative of Pm(x) at x, is the (m-I)* Taylor polynomial of f(x) at x, . Let us consider some examples now. Example 1 : Let us find the Taylor polynomials of We apply Theorem 1 with x, = 3. Applications of Partial since eO)(3) = f(3) = 22, Derivatives e') (3) = 19, en (3) = 6 and 19 Po (x) = 22, P, (x) = 22 + (x - 3), 19 14 6 P3 (x) = 22 + (x-3) + -2! (x-3)' + -3! (x-3)l and P, (x) = P3 (x) for all r > 3. b Example 2 :Let us find the fourth Taylor polynomial 1 1 We have f(x) =- (1 + x)-' 2 1 1 3 15 Therefore, f(0) = 1, f (0) = , f" (0) = - (0) = - ti4)(0) = - - 2 -4 ' e3) 8 ' 16 - The desired polynomial is f (0) f"(0) (0) x3 + ff4I (0) 4 T4(x) = f(0) +--- x+- x2+ l! 2! 3! 4! Example 3 : Let us find T, (x) for cos x at x, = z. Now cos x = - 1 and the first eight derivatives of cos x at x are Dropping the terms with coefficients 0, we have the polynomial 1 .Example 4 :Let us find T5 (x) at x, = 0 for f, where f(x) = -= (1 - x)-' 1-x Computing the derivatives, we obtain f. (x) = (1 - x)-~,f' (x) = 2(1-~)-~. r3)(x) = 3.2 (I-X)~, f4' (x) = 4 ! ( l-x)" P" (x) = 5! (1 - x)~ Thus, the successive derivatives off at 0 , in order, are Since f(0) = 1, we obtain Taylor's Theorem = 1 +x+x2+x3+x4+x5 Now you can try these exercises. El) Find the nthTaylor polynomial of the function ex at x = 2. E2) Find the 6" Taylor polynomial of sin x at x = 0. E3) Find the rh Taylor polynomials of the following functions at the indicated point and for the indicated value of r. E4) Find a polynomial f(x) of degree 2 that satisfies f(1) = 2, f (1) = -1 and f' (1) = 2. We now state Taylor's theorem which gives us the connection between a function and its Taylor polynomials at a point.
Load more

Recommended publications
  • Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder
    Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder September 11, 2018 Prof. Michael Paul Prediction Functions Remember: a prediction function is the function that predicts what the output should be, given the input. Prediction Functions Linear regression: f(x) = wTx + b Linear classification (perceptron): f(x) = 1, wTx + b ≥ 0 -1, wTx + b < 0 Need to learn what w should be! Learning Parameters Goal is to learn to minimize error • Ideally: true error • Instead: training error The loss function gives the training error when using parameters w, denoted L(w). • Also called cost function • More general: objective function (in general objective could be to minimize or maximize; with loss/cost functions, we want to minimize) Learning Parameters Goal is to minimize loss function. How do we minimize a function? Let’s review some math. Rate of Change The slope of a line is also called the rate of change of the line. y = ½x + 1 “rise” “run” Rate of Change For nonlinear functions, the “rise over run” formula gives you the average rate of change between two points Average slope from x=-1 to x=0 is: 2 f(x) = x -1 Rate of Change There is also a concept of rate of change at individual points (rather than two points) Slope at x=-1 is: f(x) = x2 -2 Rate of Change The slope at a point is called the derivative at that point Intuition: f(x) = x2 Measure the slope between two points that are really close together Rate of Change The slope at a point is called the derivative at that point Intuition: Measure the
    [Show full text]
  • Tutorial 8: Solutions
    Tutorial 8: Solutions Applications of the Derivative 1. We are asked to find the absolute maximum and minimum values of f on the given interval, and state where those values occur: (a) f(x) = 2x3 + 3x2 12x on [1; 4]. − The absolute extrema occur either at a critical point (stationary point or point of non-differentiability) or at the endpoints. The stationary points are given by f 0(x) = 0, which in this case gives 6x2 + 6x 12 = 0 = x = 1; x = 2: − ) − Checking the values at the critical points (only x = 1 is in the interval [1; 4]) and endpoints: f(1) = 7; f(4) = 128: − Therefore the absolute maximum occurs at x = 4 and is given by f(4) = 124 and the absolute minimum occurs at x = 1 and is given by f(1) = 7. − (b) f(x) = (x2 + x)2=3 on [ 2; 3] − As before, we find the critical points. The derivative is given by 2 2x + 1 f 0(x) = 3 (x2 + x)1=2 and hence we have a stationary point when 2x + 1 = 0 and points of non- differentiability whenever x2 + x = 0. Solving these, we get the three critical points, x = 1=2; and x = 0; 1: − − Checking the value of the function at these critical points and the endpoints: f( 2) = 22=3; f( 1) = 0; f( 1=2) = 2−4=3; f(0) = 0; f(3) = (12)2=3: − − − Hence the absolute minimum occurs at either x = 1 or x = 0 since in both − these cases the minimum value is 0, while the absolute maximum occurs at x = 3 and is f(3) = (12)2=3.
    [Show full text]
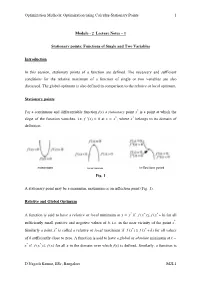
  • Lecture Notes – 1
    Optimization Methods: Optimization using Calculus-Stationary Points 1 Module - 2 Lecture Notes – 1 Stationary points: Functions of Single and Two Variables Introduction In this session, stationary points of a function are defined. The necessary and sufficient conditions for the relative maximum of a function of single or two variables are also discussed. The global optimum is also defined in comparison to the relative or local optimum. Stationary points For a continuous and differentiable function f(x) a stationary point x* is a point at which the slope of the function vanishes, i.e. f ’(x) = 0 at x = x*, where x* belongs to its domain of definition. minimum maximum inflection point Fig. 1 A stationary point may be a minimum, maximum or an inflection point (Fig. 1). Relative and Global Optimum A function is said to have a relative or local minimum at x = x* if f ()xfxh**≤+ ( )for all sufficiently small positive and negative values of h, i.e. in the near vicinity of the point x*. Similarly a point x* is called a relative or local maximum if f ()xfxh**≥+ ( )for all values of h sufficiently close to zero. A function is said to have a global or absolute minimum at x = x* if f ()xfx* ≤ ()for all x in the domain over which f(x) is defined. Similarly, a function is D Nagesh Kumar, IISc, Bangalore M2L1 Optimization Methods: Optimization using Calculus-Stationary Points 2 said to have a global or absolute maximum at x = x* if f ()xfx* ≥ ()for all x in the domain over which f(x) is defined.
    [Show full text]
  • Maxima and Minima
    Basic Mathematics Maxima and Minima R Horan & M Lavelle The aim of this document is to provide a short, self assessment programme for students who wish to be able to use differentiation to find maxima and mininima of functions. Copyright c 2004 [email protected] , [email protected] Last Revision Date: May 5, 2005 Version 1.0 Table of Contents 1. Rules of Differentiation 2. Derivatives of order 2 (and higher) 3. Maxima and Minima 4. Quiz on Max and Min Solutions to Exercises Solutions to Quizzes Section 1: Rules of Differentiation 3 1. Rules of Differentiation Throughout this package the following rules of differentiation will be assumed. (In the table of derivatives below, a is an arbitrary, non-zero constant.) y axn sin(ax) cos(ax) eax ln(ax) dy 1 naxn−1 a cos(ax) −a sin(ax) aeax dx x If a is any constant and u, v are two functions of x, then d du dv (u + v) = + dx dx dx d du (au) = a dx dx Section 1: Rules of Differentiation 4 The stationary points of a function are those points where the gradient of the tangent (the derivative of the function) is zero. Example 1 Find the stationary points of the functions (a) f(x) = 3x2 + 2x − 9 , (b) f(x) = x3 − 6x2 + 9x − 2 . Solution dy (a) If y = 3x2 + 2x − 9 then = 3 × 2x2−1 + 2 = 6x + 2. dx The stationary points are found by solving the equation dy = 6x + 2 = 0 . dx In this case there is only one solution, x = −1/3.
    [Show full text]
  • The Theory of Stationary Point Processes By
    THE THEORY OF STATIONARY POINT PROCESSES BY FREDERICK J. BEUTLER and OSCAR A. Z. LENEMAN (1) The University of Michigan, Ann Arbor, Michigan, U.S.A. (3) Table of contents Abstract .................................... 159 1.0. Introduction and Summary ......................... 160 2.0. Stationarity properties for point processes ................... 161 2.1. Forward recurrence times and points in an interval ............. 163 2.2. Backward recurrence times and stationarity ................ 167 2.3. Equivalent stationarity conditions .................... 170 3.0. Distribution functions, moments, and sample averages of the s.p.p ......... 172 3.1. Convexity and absolute continuity .................... 172 3.2. Existence and global properties of moments ................ 174 3.3. First and second moments ........................ 176 3.4. Interval statistics and the computation of moments ............ 178 3.5. Distribution of the t n .......................... 182 3.6. An ergodic theorem ........................... 184 4.0. Classes and examples of stationary point processes ............... 185 4.1. Poisson processes ............................ 186 4.2. Periodic processes ........................... 187 4.3. Compound processes .......................... 189 4.4. The generalized skip process ....................... 189 4.5. Jitte processes ............................ 192 4.6. ~deprendent identically distributed intervals ................ 193 Acknowledgments ............................... 196 References ................................... 196 Abstract An axiomatic formulation is presented for point processes which may be interpreted as ordered sequences of points randomly located on the real line. Such concepts as forward recurrence times and number of points in intervals are defined and related in set-theoretic Q) Presently at Massachusetts Institute of Technology, Lexington, Mass., U.S.A. (2) This work was supported by the National Aeronautics and Space Administration under research grant NsG-2-59. 11 - 662901. Aeta mathematica. 116. Imprlm$ le 19 septembre 1966.
    [Show full text]
  • Calculus 120, Section 7.3 Maxima & Minima of Multivariable Functions
    Calculus 120, section 7.3 Maxima & Minima of Multivariable Functions notes by Tim Pilachowski A quick note to start: If you’re at all unsure about the material from 7.1 and 7.2, now is the time to go back to review it, and get some help if necessary. You’ll need all of it for the next three sections. Just like we had a first-derivative test and a second-derivative test to maxima and minima of functions of one variable, we’ll use versions of first partial and second partial derivatives to determine maxima and minima of functions of more than one variable. The first derivative test for functions of more than one variable looks very much like the first derivative test we have already used: If f(x, y, z) has a relative maximum or minimum at a point ( a, b, c) then all partial derivatives will equal 0 at that point. That is ∂f ∂f ∂f ()a b,, c = 0 ()a b,, c = 0 ()a b,, c = 0 ∂x ∂y ∂z Example A: Find the possible values of x, y, and z at which (xf y,, z) = x2 + 2y3 + 3z 2 + 4x − 6y + 9 has a relative maximum or minimum. Answers : (–2, –1, 0); (–2, 1, 0) Example B: Find the possible values of x and y at which fxy(),= x2 + 4 xyy + 2 − 12 y has a relative maximum or minimum. Answer : (4, –2); z = 12 Notice that the example above asked for possible values. The first derivative test by itself is inconclusive. The second derivative test for functions of more than one variable is a good bit more complicated than the one used for functions of one variable.
    [Show full text]
  • Mean Value, Taylor, and All That
    Mean Value, Taylor, and all that Ambar N. Sengupta Louisiana State University November 2009 Careful: Not proofread! Derivative Recall the definition of the derivative of a function f at a point p: f (w) − f (p) f 0(p) = lim (1) w!p w − p Derivative Thus, to say that f 0(p) = 3 means that if we take any neighborhood U of 3, say the interval (1; 5), then the ratio f (w) − f (p) w − p falls inside U when w is close enough to p, i.e. in some neighborhood of p. (Of course, we can’t let w be equal to p, because of the w − p in the denominator.) In particular, f (w) − f (p) > 0 if w is close enough to p, but 6= p. w − p Derivative So if f 0(p) = 3 then the ratio f (w) − f (p) w − p lies in (1; 5) when w is close enough to p, i.e. in some neighborhood of p, but not equal to p. Derivative So if f 0(p) = 3 then the ratio f (w) − f (p) w − p lies in (1; 5) when w is close enough to p, i.e. in some neighborhood of p, but not equal to p. In particular, f (w) − f (p) > 0 if w is close enough to p, but 6= p. w − p • when w > p, but near p, the value f (w) is > f (p). • when w < p, but near p, the value f (w) is < f (p). Derivative From f 0(p) = 3 we found that f (w) − f (p) > 0 if w is close enough to p, but 6= p.
    [Show full text]
  • Math 105: Multivariable Calculus Seventeenth Lecture (3/17/10)
    Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Math 105: Multivariable Calculus Seventeenth Lecture (3/17/10) Steven J Miller Williams College [email protected] http://www.williams.edu/go/math/sjmiller/ public html/341/ Bronfman Science Center Williams College, March 17, 2010 1 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Summary for the Day 2 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Summary for the day Fast Taylor Series. Critical Points and Extrema. Constrained Maxima and Minima. 3 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Fast Taylor Series 4 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Formula for Taylor Series Notation: f twice differentiable function ∂f ∂f Gradient: f =( ∂ ,..., ∂ ). ∇ x1 xn Hessian: ∂2f ∂2f ∂x1∂x1 ∂x1∂xn . ⋅⋅⋅. Hf = ⎛ . .. ⎞ . ∂2f ∂2f ⎜ ∂ ∂ ∂ ∂ ⎟ ⎝ xn x1 ⋅⋅⋅ xn xn ⎠ Second Order Taylor Expansion at −→x 0 1 T f (−→x 0) + ( f )(−→x 0) (−→x −→x 0)+ (−→x −→x 0) (Hf )(−→x 0)(−→x −→x 0) ∇ ⋅ − 2 − − T where (−→x −→x 0) is the row vector which is the transpose of −→x −→x 0. − − 5 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Example 3 Let f (x, y)= sin(x + y) + (x + 1) y and (x0, y0) = (0, 0). Then ( f )(x, y) = cos(x + y)+ 3(x + 1)2y, cos(x + y) + (x + 1)3 ∇ and sin(x + y)+ 6(x + 1)2y sin(x + y)+ 3(x + 1)2 (Hf )(x, y) = − − , sin(x + y)+ 3(x + 1)2 sin(x + y) − − so 0 3 f (0, 0)= 0, ( f )(0, 0) = (1, 2), (Hf )(0, 0)= ∇ 3 0 which implies the second order Taylor expansion is 1 0 3 x 0 + (1, 2) (x, y)+ (x, y) ⋅ 2 3 0 y 1 3y = x + 2y + (x, y) = x + 2y + 3xy.
    [Show full text]
  • Lecture 13: Extrema
    Math S21a: Multivariable calculus Oliver Knill, Summer 2013 Lecture 13: Extrema An important problem in multi-variable calculus is to extremize a function f(x, y) of two vari- ables. As in one dimensions, in order to look for maxima or minima, we consider points, where the ”derivative” is zero. A point (a, b) in the plane is called a critical point of a function f(x, y) if ∇f(a, b) = h0, 0i. Critical points are candidates for extrema because at critical points, all directional derivatives D~vf = ∇f · ~v are zero. We can not increase the value of f by moving into any direction. This definition does not include points, where f or its derivative is not defined. We usually assume that a function is arbitrarily often differentiable. Points where the function has no derivatives are not considered part of the domain and need to be studied separately. For the function f(x, y) = |xy| for example, we would have to look at the points on the coordinate axes separately. 1 Find the critical points of f(x, y) = x4 + y4 − 4xy + 2. The gradient is ∇f(x, y) = h4(x3 − y), 4(y3 − x)i with critical points (0, 0), (1, 1), (−1, −1). 2 f(x, y) = sin(x2 + y) + y. The gradient is ∇f(x, y) = h2x cos(x2 + y), cos(x2 + y) + 1i. For a critical points, we must have x = 0 and cos(y) + 1 = 0 which means π + k2π. The critical points are at ... (0, −π), (0, π), (0, 3π),.... 2 2 3 The graph of f(x, y) = (x2 + y2)e−x −y looks like a volcano.
    [Show full text]
  • The First Derivative and Stationary Points
    Mathematics Learning Centre The first derivative and stationary points Jackie Nicholas c 2004 University of Sydney Mathematics Learning Centre, University of Sydney 1 The first derivative and stationary points dy The derivative of a function y = f(x) tell us a lot about the shape of a curve. In this dx section we will discuss the concepts of stationary points and increasing and decreasing functions. However, we will limit our discussion to functions y = f(x) which are well behaved. Certain functions cause technical difficulties so we will concentrate on those that don’t! The first derivative dy The derivative, dx ,isthe slope of the tangent to the curve y = f(x)atthe point x.Ifwe know about the derivative we can deduce a lot about the curve itself. Increasing functions dy If > 0 for all values of x in an interval I, then we know that the slope of the tangent dx to the curve is positive for all values of x in I and so the function y = f(x)isincreasing on the interval I. 3 For example, let y = x + x, then y dy 1 =3x2 +1> 0 for all values of x. dx That is, the slope of the tangent to the x curve is positive for all values of x. So, –1 0 1 y = x3 + x is an increasing function for all values of x. –1 The graph of y = x3 + x. We know that the function y = x2 is increasing for x>0. We can work this out from the derivative. 2 If y = x then y dy 2 =2x>0 for all x>0.
    [Show full text]
  • EE2 Maths: Stationary Points
    EE2 Maths: Stationary Points df Univariate case: When we maximize f(x) (solving for the x0 such that dx = 0) the d df gradient is zero at these points. What about the rate of change of gradient: dx ( dx ) at the minimum x0? For a minimum the gradient increases as x0 ! x0 + ∆x (∆x > 0). It follows d2f d2f that dx2 > 0. The opposite is true for a maximum: dx2 < 0, the gradient decreases upon d2f positive steps away from x0. For a point of inflection dx2 = 0. r @f @f Multivariate case: Stationary points occur when f = 0. In 2-d this is ( @x ; @y ) = 0, @f @f namely, a generalization of the univariate case. Recall that df = @x dx + @y dy can be written as df = ds · rf where ds = (dx; dy). If rf = 0 at (x0; y0) then any infinitesimal step ds away from (x0; y0) will still leave f unchanged, i.e. df = 0. There are three types of stationary points of f(x; y): Maxima, Minima and Saddle Points. We'll draw some of their properties on the board. We will now attempt to find ways of identifying the character of each of the stationary points of f(x; y). Consider a Taylor expansion about a stationary point (x0; y0). We know that rf = 0 at (x0; y0) so writing (∆x; ∆y) = (x − x0; y − y0) we find: − ∆f = f(x; y)[ f(x0; y0) ] 1 @2f @2f @2f ' 0 + (∆x)2 + 2 ∆x∆y + (∆y)2 : (1) 2! @x2 @x@y @y2 Maxima: At a maximum all small steps away from (x0; y0) lead to ∆f < 0.
    [Show full text]
  • Some Recent Developments in the Calculus of Variations.*
    1920.] THE CALCULUS OF VARIATIONS. 343 SOME RECENT DEVELOPMENTS IN THE CALCULUS OF VARIATIONS.* BY PROFESSOR GILBERT AMES BLISS. IT is my purpose to speak this afternoon of a part of the theory of the calculus of variations which has aroused the interest and taxed the ingenuity of a sequence of mathe­ maticians beginning with Legendre, and extending by way of Jacobi, Clebsch, Weierstrass, and a numerous array of others, to the present time. The literature of the subject is very large and is still growing. I was discussing recently the title of this address with a fellow mathematician who remarked that he was not aware that there had been any recent progress in the calculus of variations. This was a very natural sus­ picion, I think, in view of the fact that the attention of most mathematicians of the present time seems irresistibly attracted to such subjects as integral equations and their generaliza­ tions, the theory of definite integration, and the theory of functions of lines. It is indeed in these latter domains that the activities especially characteristic of the present era are centered, and the progress already made in them, and the further progress inevitable in the near future, will doubtless be sufficient alone to insure for our generation of mathematical workers a noteworthy place in the history of the science. While speaking of present day mathematical tendencies I should like to take occasion to mention a remark which has been made to me a number of times by persons who are inter­ ested in mathematics primarily for its applications.
    [Show full text]