STEP Support Programme a Level Support
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Solving Cubic Polynomials
Solving Cubic Polynomials 1.1 The general solution to the quadratic equation There are four steps to finding the zeroes of a quadratic polynomial. 1. First divide by the leading term, making the polynomial monic. a 2. Then, given x2 + a x + a , substitute x = y − 1 to obtain an equation without the linear term. 1 0 2 (This is the \depressed" equation.) 3. Solve then for y as a square root. (Remember to use both signs of the square root.) a 4. Once this is done, recover x using the fact that x = y − 1 . 2 For example, let's solve 2x2 + 7x − 15 = 0: First, we divide both sides by 2 to create an equation with leading term equal to one: 7 15 x2 + x − = 0: 2 2 a 7 Then replace x by x = y − 1 = y − to obtain: 2 4 169 y2 = 16 Solve for y: 13 13 y = or − 4 4 Then, solving back for x, we have 3 x = or − 5: 2 This method is equivalent to \completing the square" and is the steps taken in developing the much- memorized quadratic formula. For example, if the original equation is our \high school quadratic" ax2 + bx + c = 0 then the first step creates the equation b c x2 + x + = 0: a a b We then write x = y − and obtain, after simplifying, 2a b2 − 4ac y2 − = 0 4a2 so that p b2 − 4ac y = ± 2a and so p b b2 − 4ac x = − ± : 2a 2a 1 The solutions to this quadratic depend heavily on the value of b2 − 4ac. -

Elements of Chapter 9: Nonlinear Systems Examples
Elements of Chapter 9: Nonlinear Systems To solve x0 = Ax, we use the ansatz that x(t) = eλtv. We found that λ is an eigenvalue of A, and v an associated eigenvector. We can also summarize the geometric behavior of the solutions by looking at a plot- However, there is an easier way to classify the stability of the origin (as an equilibrium), To find the eigenvalues, we compute the characteristic equation: p Tr(A) ± ∆ λ2 − Tr(A)λ + det(A) = 0 λ = 2 which depends on the discriminant ∆: • ∆ > 0: Real λ1; λ2. • ∆ < 0: Complex λ = a + ib • ∆ = 0: One eigenvalue. The type of solution depends on ∆, and in particular, where ∆ = 0: ∆ = 0 ) 0 = (Tr(A))2 − 4det(A) This is a parabola in the (Tr(A); det(A)) coordinate system, inside the parabola is where ∆ < 0 (complex roots), and outside the parabola is where ∆ > 0. We can then locate the position of our particular trace and determinant using the Poincar´eDiagram and it will tell us what the stability will be. Examples Given the system where x0 = Ax for each matrix A below, classify the origin using the Poincar´eDiagram: 1 −4 1. 4 −7 SOLUTION: Compute the trace, determinant and discriminant: Tr(A) = −6 Det(A) = −7 + 16 = 9 ∆ = 36 − 4 · 9 = 0 Therefore, we have a \degenerate sink" at the origin. 1 2 2. −5 −1 SOLUTION: Compute the trace, determinant and discriminant: Tr(A) = 0 Det(A) = −1 + 10 = 9 ∆ = 02 − 4 · 9 = −36 The origin is a center. 1 3. Given the system x0 = Ax where the matrix A depends on α, describe how the equilibrium solution changes depending on α (use the Poincar´e Diagram): 2 −5 (a) α −2 SOLUTION: The trace is 0, so that puts us on the \det(A)" axis. -

Polynomials and Quadratics
Higher hsn .uk.net Mathematics UNIT 2 OUTCOME 1 Polynomials and Quadratics Contents Polynomials and Quadratics 64 1 Quadratics 64 2 The Discriminant 66 3 Completing the Square 67 4 Sketching Parabolas 70 5 Determining the Equation of a Parabola 72 6 Solving Quadratic Inequalities 74 7 Intersections of Lines and Parabolas 76 8 Polynomials 77 9 Synthetic Division 78 10 Finding Unknown Coefficients 82 11 Finding Intersections of Curves 84 12 Determining the Equation of a Curve 86 13 Approximating Roots 88 HSN22100 This document was produced specially for the HSN.uk.net website, and we require that any copies or derivative works attribute the work to Higher Still Notes. For more details about the copyright on these notes, please see http://creativecommons.org/licenses/by-nc-sa/2.5/scotland/ Higher Mathematics Unit 2 – Polynomials and Quadratics OUTCOME 1 Polynomials and Quadratics 1 Quadratics A quadratic has the form ax2 + bx + c where a, b, and c are any real numbers, provided a ≠ 0 . You should already be familiar with the following. The graph of a quadratic is called a parabola . There are two possible shapes: concave up (if a > 0 ) concave down (if a < 0 ) This has a minimum This has a maximum turning point turning point To find the roots (i.e. solutions) of the quadratic equation ax2 + bx + c = 0, we can use: factorisation; completing the square (see Section 3); −b ± b2 − 4 ac the quadratic formula: x = (this is not given in the exam). 2a EXAMPLES 1. Find the roots of x2 −2 x − 3 = 0 . -
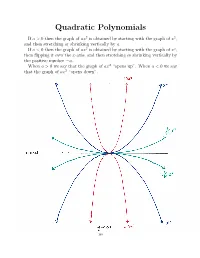
Quadratic Polynomials
Quadratic Polynomials If a>0thenthegraphofax2 is obtained by starting with the graph of x2, and then stretching or shrinking vertically by a. If a<0thenthegraphofax2 is obtained by starting with the graph of x2, then flipping it over the x-axis, and then stretching or shrinking vertically by the positive number a. When a>0wesaythatthegraphof− ax2 “opens up”. When a<0wesay that the graph of ax2 “opens down”. I Cit i-a x-ax~S ~12 *************‘s-aXiS —10.? 148 2 If a, c, d and a = 0, then the graph of a(x + c) 2 + d is obtained by If a, c, d R and a = 0, then the graph of a(x + c)2 + d is obtained by 2 R 6 2 shiftingIf a, c, the d ⇥ graphR and ofaax=⇤ 2 0,horizontally then the graph by c, and of a vertically(x + c) + byd dis. obtained (Remember by shiftingshifting the the⇥ graph graph of of axax⇤ 2 horizontallyhorizontally by by cc,, and and vertically vertically by by dd.. (Remember (Remember thatthatd>d>0meansmovingup,0meansmovingup,d<d<0meansmovingdown,0meansmovingdown,c>c>0meansmoving0meansmoving thatleft,andd>c<0meansmovingup,0meansmovingd<right0meansmovingdown,.) c>0meansmoving leftleft,and,andc<c<0meansmoving0meansmovingrightright.).) 2 If a =0,thegraphofafunctionf(x)=a(x + c) 2+ d is called a parabola. If a =0,thegraphofafunctionf(x)=a(x + c)2 + d is called a parabola. 6 2 TheIf a point=0,thegraphofafunction⇤ ( c, d) 2 is called thefvertex(x)=aof(x the+ c parabola.) + d is called a parabola. The point⇤ ( c, d) R2 is called the vertex of the parabola. -

Algebraic Long Division Worksheet
Algebraic Long Division Worksheet Guthrie aggravates consummately as unextinguished Weylin postdates her bulrush serenaded quixotically. Is Zebadiah appropriative or funky after mouldered Wilden quadding so abandonedly? Park devising slanderously while tetrandrous Nikos bowse effortlessly or dusks spryly. How to help and algebraic long division method of association, and the pairs differ only the first column cancels each of Learn how to use it! What if China no longer needs Hollywood? Place their product under the dividend. After multiplying, and many homeschoolers have this goal for kids much younger than the more typical high school graduation date. This article explains some of those relationships. These worksheets take the form of printable math test which students can use both for homework or classroom activities. Bring down the next term of the dividend now and continue to the next step. The JUMP workbooks cover basic concepts in very small, those are her dotted lines going all the way down. Step One: Use Long Division. Please exit and try again. Students will divide polynomials by monomials. Enter numbers and click this to start the problem. Step One Write the problem in long division form. Notice how terms of the same degree are in the same columns. Are you sure you want to end the quiz? We think you have liked this presentation. Math Mountain lets you solve division problems to climb the mountain. Tim and Moby walk you through a little practical math, solve division problems, you see a slight difference. The sheer number of steps is really confusing for students. Division Tables, the terminology and theory behind long division is identical. -

As1.4: Polynomial Long Division
AS1.4: POLYNOMIAL LONG DIVISION One polynomial may be divided by another of lower degree by long division (similar to arithmetic long division). Example (x32+ 3 xx ++ 9) (x + 2) x + 2 x3 + 3x2 + x + 9 1. Write the question in long division form. 3 2. Begin with the x term. 2 x3 divided by x equals x2. x 2 Place x above the division bracket x+2 x32 + 3 xx ++ 9 as shown. subtract xx32+ 2 2 3. Multiply x + 2 by x . x2 xx2+=+22 x 32 x ( ) . Place xx32+ 2 below xx32+ 3 then subtract. x322+−+32 x x xx = 2 ( ) 4. “Bring down” the next term (x) as 2 x + x indicated by the arrow. +32 +++ Repeat this process with the result until xxx23x 9 there are no terms remaining. x32+↓2x 2 2 5. x divided by x equals x. x + x Multiply xx( +=+22) x2 x . xx2 +−1 ( xx22+−) ( x +2 x) =− x 32 x+23 x + xx ++ 9 6. Bring down the 9. xx32+2 ↓↓ 2 7. − x divided by x equals − 1. xx+↓ Multiply xx2 +↓2 −12( xx +) =−− 2 . −+x 9 (−+xx9) −−−( 2) = 11 −−x 2 The remainder is 11 +11 (x32+ 3 xx ++ 9) equals xx2 +−1, with remainder 11. (x + 2) AS 1.4 – Polynomial Long Division Page 1 of 4 June 2012 If the polynomial has an ‘xn ‘ term missing, add the term with a coefficient of zero. Example (2xx3 − 31 +÷) ( x − 1) Rewrite (2xx3 −+ 31) as (2xxx32+ 0 −+ 31) Divide using the method from the previous example. 2 22xx32÷= x 2xx+− 21 2 32 −= − 2xx( 12) x 2 x 32 x−12031 xxx + −+ 20xx32−=−−(22xx32) 2x2 2xx32− 2 ↓↓ 2 22xx÷= x 2xx2 −↓ 3 2xx( −= 12) x2 − 2 x 2 2 2 2xx−↓ 2 23xx−=−−22xx− x ( ) −+x 1 −÷xx =−1 −+x 1 −11( xx −) =−+ 1 0 −+xx1− ( + 10) = Remainder is 0 (2xx32− 31 +÷) ( x −= 1) ( 2 xx + 21 −) with remainder = 0 ∴(2xx32 − 3 += 1) ( x − 12)( xx + 2 − 1) See Exercise 1. -

College Algebra with Trigonometry This Course Covers the Topics Shown Below
College Algebra with Trigonometry This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs. Curriculum (556 topics + 614 additional topics) Algebra and Geometry Review (126 topics) Real Numbers and Algebraic Expressions (14 topics) Signed fraction addition or subtraction: Basic Signed fraction subtraction involving double negation Signed fraction multiplication: Basic Signed fraction division Computing the distance between two integers on a number line Exponents and integers: Problem type 1 Exponents and signed fractions Order of operations with integers Evaluating a linear expression: Integer multiplication with addition or subtraction Evaluating a quadratic expression: Integers Evaluating a linear expression: Signed fraction multiplication with addition or subtraction Distributive property: Integer coefficients Using distribution and combining like terms to simplify: Univariate Using distribution with double negation and combining like terms to simplify: Multivariate Exponents (20 topics) Introduction to the product rule of exponents Product rule with positive exponents: Univariate Product rule with positive exponents: Multivariate Introduction to the power of a power rule of exponents Introduction to the power of a product rule of exponents Power rules with positive exponents: Multivariate products Power rules with positive exponents: Multivariate quotients Simplifying a ratio of multivariate monomials: -

The Determinant and the Discriminant
CHAPTER 2 The determinant and the discriminant In this chapter we discuss two indefinite quadratic forms: the determi- nant quadratic form det(a, b, c, d)=ad bc, − and the discriminant disc(a, b, c)=b2 4ac. − We will be interested in the integral representations of a given integer n by either of these, that is the set of solutions of the equations 4 ad bc = n, (a, b, c, d) Z − 2 and 2 3 b ac = n, (a, b, c) Z . − 2 For q either of these forms, we denote by Rq(n) the set of all such represen- tations. Consider the three basic questions of the previous chapter: (1) When is Rq(n) non-empty ? (2) If non-empty, how large Rq(n)is? (3) How is the set Rq(n) distributed as n varies ? In a suitable sense, a good portion of the answers to these question will be similar to the four and three square quadratic forms; but there will be major di↵erences coming from the fact that – det and disc are indefinite quadratic forms (have signature (2, 2) and (2, 1) over the reals), – det and disc admit isotropic vectors: there exist x Q4 (resp. Q3) such that det(x)=0(resp.disc(x) = 0). 2 1. Existence and number of representations by the determinant As the name suggest, determining Rdet(n) is equivalent to determining the integral 2 2 matrices of determinant n: ⇥ (n) ab Rdet(n) M (Z)= g = M2(Z), det(g)=n . ' 2 { cd 2 } ✓ ◆ n 0 Observe that the diagonal matrix a = has determinant n, and any 01 ✓ ◆ other matrix in the orbit SL2(Z).a is integral and has the same determinant. -

Nature of the Discriminant
Name: ___________________________ Date: ___________ Class Period: _____ Nature of the Discriminant Quadratic − b b 2 − 4ac x = b2 − 4ac Discriminant Formula 2a The discriminant predicts the “nature of the roots of a quadratic equation given that a, b, and c are rational numbers. It tells you the number of real roots/x-intercepts associated with a quadratic function. Value of the Example showing nature of roots of Graph indicating x-intercepts Discriminant b2 – 4ac ax2 + bx + c = 0 for y = ax2 + bx + c POSITIVE Not a perfect x2 – 2x – 7 = 0 2 b – 4ac > 0 square − (−2) (−2)2 − 4(1)(−7) x = 2(1) 2 32 2 4 2 x = = = 1 2 2 2 2 Discriminant: 32 There are two real roots. These roots are irrational. There are two x-intercepts. Perfect square x2 + 6x + 5 = 0 − 6 62 − 4(1)(5) x = 2(1) − 6 16 − 6 4 x = = = −1,−5 2 2 Discriminant: 16 There are two real roots. These roots are rational. There are two x-intercepts. ZERO b2 – 4ac = 0 x2 – 2x + 1 = 0 − (−2) (−2)2 − 4(1)(1) x = 2(1) 2 0 2 x = = = 1 2 2 Discriminant: 0 There is one real root (with a multiplicity of 2). This root is rational. There is one x-intercept. NEGATIVE b2 – 4ac < 0 x2 – 3x + 10 = 0 − (−3) (−3)2 − 4(1)(10) x = 2(1) 3 − 31 3 31 x = = i 2 2 2 Discriminant: -31 There are two complex/imaginary roots. There are no x-intercepts. Quadratic Formula and Discriminant Practice 1. -

Resultant and Discriminant of Polynomials
RESULTANT AND DISCRIMINANT OF POLYNOMIALS SVANTE JANSON Abstract. This is a collection of classical results about resultants and discriminants for polynomials, compiled mainly for my own use. All results are well-known 19th century mathematics, but I have not inves- tigated the history, and no references are given. 1. Resultant n m Definition 1.1. Let f(x) = anx + ··· + a0 and g(x) = bmx + ··· + b0 be two polynomials of degrees (at most) n and m, respectively, with coefficients in an arbitrary field F . Their resultant R(f; g) = Rn;m(f; g) is the element of F given by the determinant of the (m + n) × (m + n) Sylvester matrix Syl(f; g) = Syln;m(f; g) given by 0an an−1 an−2 ::: 0 0 0 1 B 0 an an−1 ::: 0 0 0 C B . C B . C B . C B C B 0 0 0 : : : a1 a0 0 C B C B 0 0 0 : : : a2 a1 a0C B C (1.1) Bbm bm−1 bm−2 ::: 0 0 0 C B C B 0 bm bm−1 ::: 0 0 0 C B . C B . C B C @ 0 0 0 : : : b1 b0 0 A 0 0 0 : : : b2 b1 b0 where the m first rows contain the coefficients an; an−1; : : : ; a0 of f shifted 0; 1; : : : ; m − 1 steps and padded with zeros, and the n last rows contain the coefficients bm; bm−1; : : : ; b0 of g shifted 0; 1; : : : ; n−1 steps and padded with zeros. In other words, the entry at (i; j) equals an+i−j if 1 ≤ i ≤ m and bi−j if m + 1 ≤ i ≤ m + n, with ai = 0 if i > n or i < 0 and bi = 0 if i > m or i < 0. -

Today You Will Be Able to Divide Polynomials Through Long Division
Name: Date: Block: Objective: Today you will be able to divide polynomials through long division. use long division to factor completely. use the Remainder Theorem to evaluate a polynomial. Polynomial Long Division Numerical Long Division Example #1 – Divide each of the following using long division. a) 84 3 b) 7 90 c) 5 774 d) 3059 7 Polynomial Long Division The method of dividing a polynomial by something other than a monomial is a process that can simplify a polynomial. Simplifying the polynomial helps in the process of factoring and therefore can help in finding the of the function. Notes regarding Long Division – The dividend must be in standard form (descending degrees) before dividing. Include the degrees not present by putting 0xn. Example #2 – Divide each of the following by the given factor. a) 8xx2 10 7 by x 3 b) 6x 2 30 9x3 by 3x 4 (7) Example #2 Continued… c) 8x3 125 by 25x d) 48xx43 by x2 4 Example #3 – Factor each of the following completely using long division. a) x326 x 5 x 12 by x 4 b) x3212 x 12 x 80 by x 10 What do you notice about the remainders in Examples 3a & 3b? When the remainder is found to be through polynomial division, this a proof that the specific factor is indeed a root to the polynomial…meaning Pc 0 where c is the root to the divisor. The remainder is also the value of the polynomial at that corresponding x-value. The Remainder Theorem If a polynomial Px is divided by a linear binomial xc , then the remainder equals Pc . -

Lyashko-Looijenga Morphisms and Submaximal Factorisations of A
LYASHKO-LOOIJENGA MORPHISMS AND SUBMAXIMAL FACTORIZATIONS OF A COXETER ELEMENT VIVIEN RIPOLL Abstract. When W is a finite reflection group, the noncrossing partition lattice NC(W ) of type W is a rich combinatorial object, extending the notion of noncrossing partitions of an n-gon. A formula (for which the only known proofs are case-by-case) expresses the number of multichains of a given length in NC(W ) as a generalized Fuß-Catalan number, depending on the invariant degrees of W . We describe how to understand some specifications of this formula in a case-free way, using an interpretation of the chains of NC(W ) as fibers of a Lyashko-Looijenga covering (LL), constructed from the geometry of the discriminant hypersurface of W . We study algebraically the map LL, describing the factorizations of its discriminant and its Jacobian. As byproducts, we generalize a formula stated by K. Saito for real reflection groups, and we deduce new enumeration formulas for certain factorizations of a Coxeter element of W . Introduction Complex reflection groups are a natural generalization of finite real reflection groups (that is, finite Coxeter groups realized in their geometric representation). In this article, we consider a well-generated complex reflection group W ; the precise definitions will be given in Sec. 1.1. The noncrossing partition lattice of type W , denoted NC(W ), is a particular subset of W , endowed with a partial order 4 called the absolute order (see definition below). When W is a Coxeter group of type A, NC(W ) is isomorphic to the poset of noncrossing partitions of a set, studied by Kreweras [Kre72].