Predicting Distribution of Malaria Vector Larval Habitats in Ethiopia by Integrating Distributed Hydrologic Modeling with Remote
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
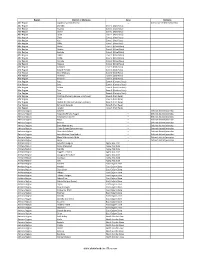
Districts of Ethiopia
Region District or Woredas Zone Remarks Afar Region Argobba Special Woreda -- Independent district/woredas Afar Region Afambo Zone 1 (Awsi Rasu) Afar Region Asayita Zone 1 (Awsi Rasu) Afar Region Chifra Zone 1 (Awsi Rasu) Afar Region Dubti Zone 1 (Awsi Rasu) Afar Region Elidar Zone 1 (Awsi Rasu) Afar Region Kori Zone 1 (Awsi Rasu) Afar Region Mille Zone 1 (Awsi Rasu) Afar Region Abala Zone 2 (Kilbet Rasu) Afar Region Afdera Zone 2 (Kilbet Rasu) Afar Region Berhale Zone 2 (Kilbet Rasu) Afar Region Dallol Zone 2 (Kilbet Rasu) Afar Region Erebti Zone 2 (Kilbet Rasu) Afar Region Koneba Zone 2 (Kilbet Rasu) Afar Region Megale Zone 2 (Kilbet Rasu) Afar Region Amibara Zone 3 (Gabi Rasu) Afar Region Awash Fentale Zone 3 (Gabi Rasu) Afar Region Bure Mudaytu Zone 3 (Gabi Rasu) Afar Region Dulecha Zone 3 (Gabi Rasu) Afar Region Gewane Zone 3 (Gabi Rasu) Afar Region Aura Zone 4 (Fantena Rasu) Afar Region Ewa Zone 4 (Fantena Rasu) Afar Region Gulina Zone 4 (Fantena Rasu) Afar Region Teru Zone 4 (Fantena Rasu) Afar Region Yalo Zone 4 (Fantena Rasu) Afar Region Dalifage (formerly known as Artuma) Zone 5 (Hari Rasu) Afar Region Dewe Zone 5 (Hari Rasu) Afar Region Hadele Ele (formerly known as Fursi) Zone 5 (Hari Rasu) Afar Region Simurobi Gele'alo Zone 5 (Hari Rasu) Afar Region Telalak Zone 5 (Hari Rasu) Amhara Region Achefer -- Defunct district/woredas Amhara Region Angolalla Terana Asagirt -- Defunct district/woredas Amhara Region Artuma Fursina Jile -- Defunct district/woredas Amhara Region Banja -- Defunct district/woredas Amhara Region Belessa -- -

Spatial Distribution of Glossina Sp. and Trypanosoma Sp. in South-Western
Duguma et al. Parasites & Vectors (2015) 8:430 DOI 10.1186/s13071-015-1041-9 RESEARCH Open Access Spatial distribution of Glossina sp. and Trypanosoma sp. in south-western Ethiopia Reta Duguma1,2, Senbeta Tasew3, Abebe Olani4, Delesa Damena4, Dereje Alemu3, Tesfaye Mulatu4, Yoseph Alemayehu5, Moti Yohannes6, Merga Bekana1, Antje Hoppenheit7, Emmanuel Abatih8, Tibebu Habtewold2, Vincent Delespaux8* and Luc Duchateau2 Abstract Background: Accurate information on the distribution of the tsetse fly is of paramount importance to better control animal trypanosomosis. Entomological and parasitological surveys were conducted in the tsetse belt of south-western Ethiopia to describe the prevalence of trypanosomosis (PoT), the abundance of tsetse flies (AT) and to evaluate the association with potential risk factors. Methods: The study was conducted between 2009 and 2012. The parasitological survey data were analysed by a random effects logistic regression model, whereas the entomological survey data were analysed by a Poisson regression model. The percentage of animals with trypanosomosis was regressed on the tsetse fly count using a random effects logistic regression model. Results: The following six risk factors were evaluated for PoT (i) altitude: significant and inverse correlation with trypanosomosis, (ii) annual variation of PoT: no significant difference between years, (iii) regional state: compared to Benishangul-Gumuz (18.0 %), the three remaining regional states showed significantly lower PoT, (iv) river system: the PoT differed significantly between the river systems, (iv) sex: male animals (11.0 %) were more affected than females (9.0 %), and finally (vi) age at sampling: no difference between the considered classes. Observed trypanosome species were T. congolense (76.0 %), T. -

Potentials and Challenges for Community Based Ecotourism Development at Haro Aba Diko Controlled Hunting Area, South Western Oromia
Journal of Resources Development and Management www.iiste.org ISSN 2422-8397 An International Peer-reviewed Journal Vol.68, 2020 Potentials and Challenges for Community Based Ecotourism Development at Haro Aba Diko Controlled Hunting Area, South Western Oromia Habib Bati Geda 1* Fanuel Kebede(PhD) 2 Dereje Denu(PhD) 3 1.Department of Ecotourism and Biodiversity conservations,Bedele college of Agriculture and Forestry,Mettu university,Ethiopia 2.Ethiopian Wild life conservation Authority 3.Department of Biology, Jimma University, Ethiopia Abstract This study was conducted to identify the potentials, Challenges of community- based ecotourism at Haro Aba Diko Controlled Hunting area, South western Ethiopia. Community -based ecotourism has become the most basic tool to meet livelihood demand across the world. Primary and secondary data were used for this study. Purposive and simple random sampling methods were used to select kebeles and 140 sample respondents respectively. To select key informant snowball method was used. Quantitative data was analyzed using frequency, percentage and mean whereas the qualitative data was used to triangulate and authenticate the study. The result of the study indicated that Haro Aba Diko Controlled Hunting area had huge resource potentials such as attractive flora and fauna ,Dabena and Didesa river with attractive cultural resource like Cultural dance, cultural food and drinks .Having this potentials community based ecotourism establishment is constrained by lack of awareness, basic infrastructures, tourism professionals and Illegal activity of community like Settlements within the Controlled Hunting Area and Conversions of forest lands to Agricultural lands. To empower the establishment of community based ecotourism, awareness creation program, promotion activity, filling gap of community social infrastructures and further study in the study area should be needed. -

Study on Spatial Distribution of Tsetse Fly and Prevalence Of
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by International Institute for Science, Technology and Education (IISTE): E-Journals Journal of Pharmacy and Alternative Medicine www.iiste.org ISSN 2222-4807 (online) ISSN 2222-5668 (Paper) An International Peer-reviewed Journal Vol.7, 2015 Study on Spatial Distribution of Tsetse Fly and Prevalence of Bovine Trypanosomosis and other Risk Factors: Case Study in Darimu District, Ilu Aba Bora Zone, Western Ethiopia Fedesa Habte Assefa Kebede Tekalegn Desta School of Veterinary Medicine, Jimma University College of Agriculture and Veterinary Medicine, P.O. Box: 307 Jimma, Ethiopia Abstract African Animal Trypanosomosis is one of the major impediments to livestock development and agricultural production in Ethiopia, which negatively affect the overall development in agriculture in general, and to food self- reliance efforts in particular. Currently, about 180,000 to 200,000km 2 of fertile arable land of west and southwest of the country is underutilized. Darimu district is one of the areas with such problems. Therefore, a cross-sectional study was conducted with the objectives of assessing the prevalence of Bovine Trypanosomosis and determines spatial distribution and apparent density of tsetse and other biting flies in the study area. In current study, a total of 650 blood samples were collected from randomly selected animals and subjected to Buffy coat parasitological laboratory technique and positive samples were subjected to thin blood smear followed by Giemsa staining. Out of the total blood sampled, 7.1% tested positive for trypanosomosis. Out of positive cases, Trypanosoma congolense (82.61%) was the dominant trypanosome species followed by mixed infection ( Trypanosoma congolense and Trypanosoma vivax ) (8.67%). -

Eastern Nile Technical Regional Office
. EASTERN NILE TECHNICAL REGIONAL OFFICE TRANSBOUNDARY ANALYSIS FINAL COUNTRY REPORT ETHIOPIA September 2006 This report was prepared by a consortium comprising Hydrosult Inc (Canada) the lead company, Tecsult (Canada), DHV (The Netherlands) and their Associates Nile Consult (Egypt), Comatex Nilotica (Sudan) and A and T Consulting (Ethiopia) DISCLAIMER The maps in this Report are provided for the convenience of the reader. The designations employed and the presentation of the material in these maps do not imply the expression of any opinion whatsoever on the part of the Eastern Nile Technical Office (ENTRO) concerning the legal or constitutional status of any Administrative Region, State or Governorate, Country, Territory or Sea Area, or concerning the delimitation of any frontier. WATERSHED MANAGEMENT CRA CONTENTS DISCLAIMER ........................................................................................................ 2 LIST OF ACRONYMS AND ABBREVIATIONS .................................................. viii EXECUTIVE SUMMARY ...................................................................................... x 1. BACKGROUND ................................................................................................ 1 1.1 Introduction ............................................................................................. 1 1.2 Primary Objectives of the Watershed Management CRA ....................... 2 1.3 The Scope and Elements of Sustainable Watershed Management ........ 4 1.3.1 Watersheds and River Basins 4 -

Ethiopia: Administrative Map (August 2017)
Ethiopia: Administrative map (August 2017) ERITREA National capital P Erob Tahtay Adiyabo Regional capital Gulomekeda Laelay Adiyabo Mereb Leke Ahferom Red Sea Humera Adigrat ! ! Dalul ! Adwa Ganta Afeshum Aksum Saesie Tsaedaemba Shire Indasilase ! Zonal Capital ! North West TigrayTahtay KoraroTahtay Maychew Eastern Tigray Kafta Humera Laelay Maychew Werei Leke TIGRAY Asgede Tsimbila Central Tigray Hawzen Medebay Zana Koneba Naeder Adet Berahile Region boundary Atsbi Wenberta Western Tigray Kelete Awelallo Welkait Kola Temben Tselemti Degua Temben Mekele Zone boundary Tanqua Abergele P Zone 2 (Kilbet Rasu) Tsegede Tselemt Mekele Town Special Enderta Afdera Addi Arekay South East Ab Ala Tsegede Mirab Armacho Beyeda Woreda boundary Debark Erebti SUDAN Hintalo Wejirat Saharti Samre Tach Armacho Abergele Sanja ! Dabat Janamora Megale Bidu Alaje Sahla Addis Ababa Ziquala Maychew ! Wegera Metema Lay Armacho Wag Himra Endamehoni Raya Azebo North Gondar Gonder ! Sekota Teru Afar Chilga Southern Tigray Gonder City Adm. Yalo East Belesa Ofla West Belesa Kurri Dehana Dembia Gonder Zuria Alamata Gaz Gibla Zone 4 (Fantana Rasu ) Elidar Amhara Gelegu Quara ! Takusa Ebenat Gulina Bugna Awra Libo Kemkem Kobo Gidan Lasta Benishangul Gumuz North Wello AFAR Alfa Zone 1(Awsi Rasu) Debre Tabor Ewa ! Fogera Farta Lay Gayint Semera Meket Guba Lafto DPubti DJIBOUTI Jawi South Gondar Dire Dawa Semen Achefer East Esite Chifra Bahir Dar Wadla Delanta Habru Asayita P Tach Gayint ! Bahir Dar City Adm. Aysaita Guba AMHARA Dera Ambasel Debub Achefer Bahirdar Zuria Dawunt Worebabu Gambela Dangura West Esite Gulf of Aden Mecha Adaa'r Mile Pawe Special Simada Thehulederie Kutaber Dangila Yilmana Densa Afambo Mekdela Tenta Awi Dessie Bati Hulet Ej Enese ! Hareri Sayint Dessie City Adm. -

OROMIA REGION - Regional 3W Map 07 December 2010
OROMIA REGION - Regional 3W Map 07 December 2010 CRS I SC-UK V Legend W Amhara S d S Farm Africa R S i E R C Benishangul R A V E CRS CARE MfM C GOAL C P n R W S o i I International Boundary SC-Denmark A , t Gumuz Afar C L c C P K Action Aid C A CARE Welthungerhilfe A CRS S U I M - I ! O C C IMC S S G S a CARE A WVE S Regional Boundary , SC-Denmark R R c m i SC-Denmark Dera C C a S r R f u u u c i C U E A Action Aid t r S m r n u f GOAL e R m R a r A m E IMC r i E C A b a I L L a R R Zonal Boundary K CARE ! f F o C Action Aid H s A a Hidabu Abote m r ! A A g a A r J x a a e A a C r Christian Aid C O d a C d r m O a r b O IMC Action Aid i W a M CA RE o J e I a G F G G G u e ! g L t n b r b e i a i i n i J o E S m u D a d Farm Africa Gerar Jarso R CARE Woreda Boundary E IMC u e p Kuyu E a ! Kiltu Kara m A i n ! o R ! S R C r ! a L Abay Chomen B Debre Libanos o ! Abuna G/Beret A M m M e A H e l o C en a m ks e ina r u Yaya Gulele Abichuna Gne'a C Ch Abe Dongoro ! a h s ! e i t c r a g f a u Nejo t IMC a ! r CRS No Data /No Intervention g E J ! W ! l a x Kombolcha o e R o ! d V e O b B i o ! ! s Guduru G J ib it Goro Gutu ! a r m b a Gudetu Kondole FHI Ke W a Mercy Corps b a s B u i ! r B Boji Dirmeji o t a Bila Seyo e i ! a r Jimma Genete l J d K L e g t s l Jeldu u E a ! d D ! u F Haro Maya e Guto Gida b M S u A m A o e B e M l R i d ! Boji Chekorsa Jimma Rare S ! D CARE GOAL CRS b a B b u A o Aleltu l e ! Kurfa Chele A g I O u f e e y G i u a S Mieso r Agriculture & Livestock i C r s t ! T a Mida KegnA a M Lalo Asabi im r K a ! ! G S Gobu -

Flow Regime and Land Cover Changes in the Didessa Sub-Basin of the Blue Nile River, South - Western Ethiopia
Flow Regime and Land Cover Changes In the Didessa Sub-Basin of the Blue Nile River, South - Western Ethiopia: Combining Empirical Analysis and Community Perception Swedish University of Agricultural Sciences Master thesis Study (EX0658) Integrated Water Resource Management Program Department of Aquatic Science and Assessment Department of Urban and Rural Development Swedish University of Agricultural Sciences (SLU) Uppsala, 2011 Sweden Sima, Bizuneh Admassu Flow Regime and Land Cover Changes in the Didessa Sub-Basin of the Blue Nile River, South-Western Ethiopia: Combining Empirical Analysis and Community Perception EX0658 Master Thesis in Integrated Water Resource Management, 30hp, Master E, Department of Aquatic Science and Assessment Department of Urban and Rural Development SLU, Swedish University of Agricultural Sciences Uppsala, 2011 Sima, Bizuneh Admassu Supervisors: Kevin Bishop Professor of Environmental Assessment Department of Aquatic Science and Assessment Swedish University of Agricultural Sciences Solomon Gebrehiwot Doctoral Student Department of Aquatic Science and Assessment Swedish University of Agricultural Sciences Uppsala Examiners Nadarajah Sriskandarajah Professor of Environmental Communication Department of Urban and Rural Development Swedish University of Agricultural Sciences Ashok Swain Director, Uppsala Center for Sustainable Development Professor of Peace and Conflict Research Department of Peace and Conflict Research Uppsala University Uppsala Key words: Ethiopia, Blue Nile, Didessa Sub-basin, Flow Regime, land cover change, Community Perception E-mail Address of the Author: [email protected] / [email protected] Acknowledgement First and foremost I would like to express my sincere thankfulness to my main thesis supervisor Professor Kevin Bishop for financial support of my stay in the field, patient guidance, excellent and critical supervision and ever reaching cooperation during the all process of this thesis work. -

Benishangul-Gumuz Region
Situation Analysis of Children and Women: Benishangul-Gumuz Region Situation Analysis of Children and Women: Benishangul-Gumuz Region ABSTRACT The Situation Analysis covers selected dimensions of child well-being in Benishangul-Gumuz Regional State. It builds on the national Situation Analysis of Children and Women in Ethiopia (2019) and on other existing research, with inputs from specialists in Government, UNICEF Ethiopia and other partners. It has an estimated population of approximately 1.1 million people, which constitutes 1.1% of the total Ethiopian population. The population is young: 13 per cent is under-five years of age and 44 per cent is under 18 years of age. Since 1999/00, Benishangul-Gumuz has experienced an impressive 28 percentage point decline in monetary poverty, but 27 per cent of the population are still poor; the second highest in the country after Tigray and higher than the national average of 24 per cent. SITUATION ANALYSIS OF CHILDREN AND WOMEN: BENISHANGUL-GUMUZ REGION 4 Food poverty continued a steep decline from 55 per cent in 1999/00 to 24 per cent in 2015/16; close to the national average of 25 per cent. In Benishangul-Gumuz, in 2014, only 1.1 per cent of rural households were in the PSNP compared to 11 per cent of households at the national level In 2011, the under-five mortality rate in Benishangul-Gumuz was the highest in Ethiopia (169 per 1,000 live births); this declined significantly, but is still very high: 96 deaths per 1,000 births, which is the second highest in the country after Afar. -

Rapport De La Cellule De Production
ENIDS / Feasibility Study DB /Final Report /2010 Financed by AfDB Nile Basin Initiative Eastern Nile Subsidiary Action Program (ENSAP) Eastern Nile Technical Regional Office (ENTRO) Eastern Nile Irrigation and Drainage Studies Feasibility Study Dinger Bereha Final Report ANNEX 1: CLIMATE, HYDROLOGY AND GROUNDWATER RESOURCES RESOUERMAINREPORT May 2010 SHORACONSULT Co. Eastern Nile Technical Regional Office (ENTRO) Disclaimer The designations employed and the presentation of materials in this present document do not imply the expression of any opinion whatsoever on the part of the Nile Basin Initiative nor the Eastern Nile Technical Regional Office concerning the legal or development status of any country, territory, city or area or its authorities, or concerning the delimitation of its frontiers or boundaries. -------------------------------------------------------------------------------------------------------------------------------------------- MCE BRLi SHORACONSULT ENIDS / FEASIBILITY STUDY / EXECUTIVE SUMMARY DINGER BEREHA PROJECT Eastern Nile Technical Regional Office (ENTRO) Page 1 EASTERN NILE IRRIGATION AND DRAINAGE STUDY/FEASIBILITY STUDY DINGER BEREHA IRRIGATION PROJECT ANNEX 1: CLIMATE, HYDROLOGY, AND GROUND WATER RESOURCES Table of contents 1. CLIMATOLOGY ........................................................................... 5 1.1 Introduction 5 1.2 Climate 5 1.3 Hydrology 6 1.4 Climate in the Project Area 7 1.4.1 General 7 1.4.2 Air temperature 7 1.4.3 Air humidity 7 1.4.4 Wind speed 7 1.4.5 Sunshine Hours 8 1.5 Rainfall Analysis 9 1.5.1 General 9 1.5.2 Rainfall Internal and External Consistency 9 1.5.3 Estimation of Rainfall Reliability Level 12 1.5.4 Estimation of ETo 14 1.5.5 Rainfall Intensity 17 1.5.6 Drainage Design 20 2. HYDROLOGY ........................................................................... -

Economic Implication of Modern Behive at Gechi District, Southwestern Ethiopia
Journal of Agricultural Economics and Development Vol. 7(2), pp. 006-010, July 2019 Available online at http://academeresearchjournals.org/journal/jaed ISSN 2327-3151 ©2019 Academe Research Journals Full Length Research Paper Economic implication of modern behive at Gechi district, Southwestern Ethiopia Esayas Negasa Hambisa Department of Agribusiness and Value Chain Management, Mettu University, P. O. Box: 318, Mettu, Ethiopia. *Corresponding author. Email: [email protected] Accepted 31 March, 2019 This study was conducted to analyze economic importance of modern bee hive at household level in Gechi District of Buno Bedele zone, Southwestern Ethiopia with an objectives of comparing modern and traditional beekeepers in economic benefit, identifing the determinants of modern beehive use and level of income and evaluate the implication of modern beehive in social issues at household level. Multi-stage random sampling technique was implemented to select the representative sample techniques. Both the primary and secondary data was used during data collection. A total of 60 household from three kebeles were selected for interview. Data obtained were analyzed using descriptive statistics and econometrics analysis. Heckman regression a method is used to analysis the determinants of modern beekeeping use and level of income. The results of the study indicated that driving force to have bee colonies comprises 93.5% for income and 6.5% for consumption purpose. It showed that the average income of households with modern beekeeping (Birr 4570.4/household) was significantly (p<0.01) higher than those households with traditional beekeeping (Birr 1804.8/household). Despite relative investment in using modern beekeeping, households’ gross income increased by 250% compared to the traditional beekeepers. -

Study on Bovine Trypanosomosis and Tse Tse Fly Challenge in Darimu District of Birbir Valley, South Western Ethiopia
Open Access Journal of Veterinary Science & Research ISSN: 2474-9222 Study on Bovine Trypanosomosis and Tse Tse Fly Challenge in Darimu District of Birbir Valley, South Western Ethiopia Teferi Benti* and Biniam Tadesse Research Article National Animal Health Diagnostic and Investigation Center, Sebeta, Ethiopia Volume 3 Issue 1 Received Date: March 08, 2018 *Corresponding author: Teferi Benti, 1National Animal Health Diagnostic and Published Date: March 29, 2018 Investigation Center, Sebeta, Ethiopia, Tel: +251911023089; Email: [email protected] Abstract This study was undertaken on bovine trypanosomiasis and its vectors at Birbir valley located in Darmu district, Illubababor zone. The parasitological examination was conducted using Buffy coat technique while vector survey was conducted using odour baited Monopyramidal trap. The objective of the study was to determine the prevalence of trypanosomiasis in cattle, to determine fly density and to identify associated risk factors. From 392 Blood samples were collected, 45(11.5%) were found to be positive by Buffy coat technique and trypanosome species identified by their motility were T.congolense 40 (88.9%) and T.vivax 5(11.1 %) and Trypanosoma congolense was the dominant species. A total of 52 Monopyramidal traps were deployed and 1836 (73%) tsetse flies and 676(26.9%) biting flies were caught. From flies captured, 971(52.9%), 540(29.4%) and 325(17.7%) Glossina morsitans sub morsitans of savannah flies, Glossina fuscipes fuscipes of reverine and Glossina pallidipes of savannah species were identified respectively. The overall apparent densities fly / trap / day (FTD) were 17.7 and 6.5 for tsetse and biting flies respectively. There was no statically significant difference (P > 0.05) in the prevalence of trypanosome infection between sex group while statistically significant difference was observed between age group(x2=41.0, p=0.000, p<0.05).