DOCSLIB.ORG

Neural Networks Learning the Network: Part 2

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Neural Networks Learning the Network: Part 2 Neural Networks Learning the network: Part 2 11-785, Fall 2020 Lecture 4 1 Recap: Universal approximators • Neural networks are universal approximators – Can approximate any function • Provided they have sufficient architecture – We have to determine the weights and biases to make them model the function 2 Recap: Approach • Define a divergence between the actual output and desired output of the network – Must be differentiable: can quantify how much a miniscule change of changes • Make all neuronal activations differentiable – Differentiable: can quantify how much a miniscule change of changes • Differentiability – enables us to determine if a small change in any parameter of the network is increasing or decreasing – Will let us optimize the network 3 Recap: The expected divergence • Minimize the expected “divergence” between the output of the net and the desired function over the input space 4 Recap: Emipirical Risk Minimization • Problem: Computing the expected divergence requires knowledge of at all which we will not have • Solution: Approximate it by the average divergence over a large number of “training” samples drawn from • Estimate the parameters to minimize this “loss” instead 5 Problem Statement • Given a training set of input-output pairs • Minimize the following function w.r.t • This is problem of function minimization – An instance of optimization 6 • A CRASH COURSE ON FUNCTION OPTIMIZATION 7 A brief note on derivatives.. derivative • A derivative of a function at any point tells us how much a minute increment to the argument of the function will increment the value of the function . For any expressed as a multiplier to a tiny increment to obtain the increments to the output . Based on the fact that at a fine enough resolution, any smooth, continuous function is locally linear at any point 8 Scalar function of scalar argument • When and are scalar . Derivative: . Often represented (using somewhat inaccurate notation) as . Or alternately (and more reasonably) as 9 Multivariate scalar function: Scalar function of vector argument Note: is now a vector • Giving us that is a row vector: • The partial derivative gives us how increments when only is incremented • Often represented as 10 Multivariate scalar function: Scalar function of vector argument Note: is now a vector We will be using this • Where symbol for vector and matrix derivatives o You may be more familiar with the term “gradient” which is actually defined as the transpose of the derivative 11 Caveat about following slides • The following slides speak of optimizing a function w.r.t a variable “x” • This is only mathematical notation. In our actual network optimization problem we would be optimizing w.r.t. network weights “w” • To reiterate – “x” in the slides represents the variable that we’re optimizing a function over and not the input to a neural network • Do not get confused! 12 The problem of optimization f(x) global maximum inflection point local minimum global minimum x • General problem of optimization: find the value of x where f(x) is minimum 13 Finding the minimum of a function f(x) x • Find the value at which = 0 – Solve • The solution is a “turning point” – Derivatives go from positive to negative or vice versa at this point • But is it a minimum? 14 Turning Points 0 0 - + - + - - + - + - + - + - + - + - -- + - - 0 • Both maxima and minima have zero derivative • Both are turning points 15 Derivatives of a curve f’(x) f(x) x • Both maxima and minima are turning points • Both maxima and minima have zero derivative 16 Derivative of the derivative of the curve f’’(x) f’(x) f(x) x • Both maxima and minima are turning points • Both maxima and minima have zero derivative • The second derivative f’’(x) is –ve at maxima and +ve at minima! 17 Solution: Finding the minimum or maximum of a function f(x) x • Find the value at which = 0: Solve • The solution is a turning point • Check the double derivative at : compute • If is positive is a minimum, otherwise it is a maximum 18 A note on derivatives of functions of single variable maximum • All locations with zero Inflection point derivative are critical points minimum – These can be local maxima, local minima, or inflection points Critical points • The second derivative is – Positive (or 0) at minima – Negative (or 0) at maxima – Zero at inflection points • It’s a little more complicated for Derivative is 0 functions of multiple variables 19 A note on derivatives of functions of single variable maximum • All locations with zero Inflection point derivative are critical points minimum – These can be local maxima, local minima, or inflection points • The second derivative is – at minima – at maxima – Zero at inflection points positive zero • It’s a little more complicated for functions of multiple variables.. negative 20 What about functions of multiple variables? • The optimum point is still “turning” point – Shifting in any direction will increase the value – For smooth functions, miniscule shifts will not result in any change at all • We must find a point where shifting in any direction by a microscopic amount will not change the value of the function 21 A brief note on derivatives of multivariate functions 22 The Gradient of a scalar function • The derivative of a scalar function of a multi-variate input is a multiplicative factor that gives us the change in for tiny variations in – The gradient is the transpose of the derivative 23 Gradients of scalar functions with multivariate inputs • Consider • Relation: This is a vector inner product. To understand its behavior lets consider a well-known property of inner products 24 A well-known vector property • The inner product between two vectors of fixed lengths is maximum when the two vectors are aligned – i.e. when 25 Properties of Gradient vs angle of Blue arrow is • • For an increment of any given length is max if is aligned with T – The function f(X) increases most rapidly if the input increment T is exactly in the direction of • The gradient is the direction of fastest increase in f(X) 26 Gradient Gradient 푇 vector 27 Gradient Gradient 푇 vector Moving in this direction increases fastest 28 Gradient Gradient 푇 vector Moving in this 푇 direction increases Moving in this fastest direction decreases fastest 29 Gradient Gradient here is 0 Gradient here is 0 30 Properties of Gradient: 2 푇 • The gradient vector is perpendicular to the level curve 31 The Hessian • The Hessian of a function is given by the second derivative 2 f 2 f 2 f 2 . x x x x x1 1 2 1 n 2 f 2 f 2 f . 2 2 x2x1 x2 x2xn X f (x1,..., xn ) : . . 2 f 2 f 2 f . 2 xnx1 xnx2 xn 32 Returning to direct optimization… 33 Finding the minimum of a scalar function of a multivariate input • The optimum point is a turning point – the gradient will be 0 34 Unconstrained Minimization of function (Multivariate) 1. Solve for the where the derivative (or gradient) equals to zero X f (X ) 0 2. Compute the Hessian Matrix at the candidate solution and verify that – Hessian is positive definite (eigenvalues positive) -> to identify local minima – Hessian is negative definite (eigenvalues negative) -> to identify local maxima 35 Closed Form Solutions are not always available f(X) X • Often it is not possible to simply solve – The function to minimize/maximize may have an intractable form • In these situations, iterative solutions are used – Begin with a “guess” for the optimal and refine it iteratively until the correct value is obtained 36 Iterative solutions f(X) X x0 x1 x2 x5 x3 x4 • Iterative solutions – Start from an initial guess for the optimal – Update the guess towards a (hopefully) “better” value of – Stop when no longer decreases • Problems: – Which direction to step in – How big must the steps be 37 The Approach of Gradient Descent • Iterative solution: – Start at some point – Find direction in which to shift this point to decrease error • This can be found from the derivative of the function – A negative derivative moving right decreases error – A positive derivative moving left decreases error – Shift point in this direction 38 The Approach of Gradient Descent • Iterative solution: Trivial algorithm . Initialize . While • If is positive: 푥 = 푥 − 푠푡푒푝 • Else 푥 = 푥 + 푠푡푒푝 – What must step be to ensure we actually get to the optimum?39 The Approach of Gradient Descent • Iterative solution: Trivial algorithm . Initialize . While • Identical to previous algorithm 40 The Approach of Gradient Descent • Iterative solution: Trivial algorithm . Initialize . While • is the “step size” 41 Gradient descent/ascent (multivariate) • The gradient descent/ascent method to find the minimum or maximum of a function iteratively – To find a maximum move in the direction of the gradient – To find a minimum move exactly opposite the direction of the gradient • Many solutions for step size 42 Gradient descent convergence criteria • The gradient descent algorithm converges when one of the following criteria is satisfied k+1 k f (x )- f (x ) < e1 • Or k x f (x ) < e 2 43 Overall Gradient Descent Algorithm • Initialize: . • do . • while 44 Convergence of Gradient Descent • For appropriate step size, for convex (bowl- shaped) functions gradient descent will always find the minimum. • For non-convex functions it will find a local minimum or an inflection point 45 • Returning to our problem.. 46 Problem Statement • Given a training set of input-output pairs • Minimize the following function w.r.t • This is problem of function minimization – An instance
Load more

Recommended publications
  • Training Autoencoders by Alternating Minimization
    Under review as a conference paper at ICLR 2018 TRAINING AUTOENCODERS BY ALTERNATING MINI- MIZATION Anonymous authors Paper under double-blind review ABSTRACT We present DANTE, a novel method for training neural networks, in particular autoencoders, using the alternating minimization principle. DANTE provides a distinct perspective in lieu of traditional gradient-based backpropagation techniques commonly used to train deep networks. It utilizes an adaptation of quasi-convex optimization techniques to cast autoencoder training as a bi-quasi-convex optimiza- tion problem. We show that for autoencoder configurations with both differentiable (e.g. sigmoid) and non-differentiable (e.g. ReLU) activation functions, we can perform the alternations very effectively. DANTE effortlessly extends to networks with multiple hidden layers and varying network configurations. In experiments on standard datasets, autoencoders trained using the proposed method were found to be very promising and competitive to traditional backpropagation techniques, both in terms of quality of solution, as well as training speed. 1 INTRODUCTION For much of the recent march of deep learning, gradient-based backpropagation methods, e.g. Stochastic Gradient Descent (SGD) and its variants, have been the mainstay of practitioners. The use of these methods, especially on vast amounts of data, has led to unprecedented progress in several areas of artificial intelligence. On one hand, the intense focus on these techniques has led to an intimate understanding of hardware requirements and code optimizations needed to execute these routines on large datasets in a scalable manner. Today, myriad off-the-shelf and highly optimized packages exist that can churn reasonably large datasets on GPU architectures with relatively mild human involvement and little bootstrap effort.
    [Show full text]
  • The Mean Value Theorem Math 120 Calculus I Fall 2015
    The Mean Value Theorem Math 120 Calculus I Fall 2015 The central theorem to much of differential calculus is the Mean Value Theorem, which we'll abbreviate MVT. It is the theoretical tool used to study the first and second derivatives. There is a nice logical sequence of connections here. It starts with the Extreme Value Theorem (EVT) that we looked at earlier when we studied the concept of continuity. It says that any function that is continuous on a closed interval takes on a maximum and a minimum value. A technical lemma. We begin our study with a technical lemma that allows us to relate 0 the derivative of a function at a point to values of the function nearby. Specifically, if f (x0) is positive, then for x nearby but smaller than x0 the values f(x) will be less than f(x0), but for x nearby but larger than x0, the values of f(x) will be larger than f(x0). This says something like f is an increasing function near x0, but not quite. An analogous statement 0 holds when f (x0) is negative. Proof. The proof of this lemma involves the definition of derivative and the definition of limits, but none of the proofs for the rest of the theorems here require that depth. 0 Suppose that f (x0) = p, some positive number. That means that f(x) − f(x ) lim 0 = p: x!x0 x − x0 f(x) − f(x0) So you can make arbitrarily close to p by taking x sufficiently close to x0.
    [Show full text]
  • AP Calculus AB Topic List 1. Limits Algebraically 2. Limits Graphically 3
    AP Calculus AB Topic List 1. Limits algebraically 2. Limits graphically 3. Limits at infinity 4. Asymptotes 5. Continuity 6. Intermediate value theorem 7. Differentiability 8. Limit definition of a derivative 9. Average rate of change (approximate slope) 10. Tangent lines 11. Derivatives rules and special functions 12. Chain Rule 13. Application of chain rule 14. Derivatives of generic functions using chain rule 15. Implicit differentiation 16. Related rates 17. Derivatives of inverses 18. Logarithmic differentiation 19. Determine function behavior (increasing, decreasing, concavity) given a function 20. Determine function behavior (increasing, decreasing, concavity) given a derivative graph 21. Interpret first and second derivative values in a table 22. Determining if tangent line approximations are over or under estimates 23. Finding critical points and determining if they are relative maximum, relative minimum, or neither 24. Second derivative test for relative maximum or minimum 25. Finding inflection points 26. Finding and justifying critical points from a derivative graph 27. Absolute maximum and minimum 28. Application of maximum and minimum 29. Motion derivatives 30. Vertical motion 31. Mean value theorem 32. Approximating area with rectangles and trapezoids given a function 33. Approximating area with rectangles and trapezoids given a table of values 34. Determining if area approximations are over or under estimates 35. Finding definite integrals graphically 36. Finding definite integrals using given integral values 37. Indefinite integrals with power rule or special derivatives 38. Integration with u-substitution 39. Evaluating definite integrals 40. Definite integrals with u-substitution 41. Solving initial value problems (separable differential equations) 42. Creating a slope field 43.
    [Show full text]
  • Anti-Chain Rule Name
    Anti-Chain Rule Name: The most fundamental rule for computing derivatives in calculus is the Chain Rule, from which all other differentiation rules are derived. In words, the Chain Rule states that, to differentiate f(g(x)), differentiate the outside function f and multiply by the derivative of the inside function g, so that d f(g(x)) = f 0(g(x)) · g0(x): dx The Chain Rule makes computation of nearly all derivatives fairly easy. It is tempting to think that there should be an Anti-Chain Rule that makes antidiffer- entiation as easy as the Chain Rule made differentiation. Such a rule would just reverse the process, so instead of differentiating f and multiplying by g0, we would antidifferentiate f and divide by g0. In symbols, Z F (g(x)) f(g(x)) dx = + C: g0(x) Unfortunately, the Anti-Chain Rule does not exist because the formula above is not Z always true. For example, consider (x2 + 1)2 dx. We can compute this integral (correctly) by expanding and applying the power rule: Z Z (x2 + 1)2 dx = x4 + 2x2 + 1 dx x5 2x3 = + + x + C 5 3 However, we could also think about our integrand above as f(g(x)) with f(x) = x2 and g(x) = x2 + 1. Then we have F (x) = x3=3 and g0(x) = 2x, so the Anti-Chain Rule would predict that Z F (g(x)) (x2 + 1)2 dx = + C g0(x) (x2 + 1)3 = + C 3 · 2x x6 + 3x4 + 3x2 + 1 = + C 6x x5 x3 x 1 = + + + + C 6 2 2 6x Since these answers are different, we conclude that the Anti-Chain Rule has failed us.
    [Show full text]
  • Curl, Divergence and Laplacian
    Curl, Divergence and Laplacian What to know: 1. The definition of curl and it two properties, that is, theorem 1, and be able to predict qualitatively how the curl of a vector field behaves from a picture. 2. The definition of divergence and it two properties, that is, if div F~ 6= 0 then F~ can't be written as the curl of another field, and be able to tell a vector field of clearly nonzero,positive or negative divergence from the picture. 3. Know the definition of the Laplace operator 4. Know what kind of objects those operator take as input and what they give as output. The curl operator Let's look at two plots of vector fields: Figure 1: The vector field Figure 2: The vector field h−y; x; 0i: h1; 1; 0i We can observe that the second one looks like it is rotating around the z axis. We'd like to be able to predict this kind of behavior without having to look at a picture. We also promised to find a criterion that checks whether a vector field is conservative in R3. Both of those goals are accomplished using a tool called the curl operator, even though neither of those two properties is exactly obvious from the definition we'll give. Definition 1. Let F~ = hP; Q; Ri be a vector field in R3, where P , Q and R are continuously differentiable. We define the curl operator: @R @Q @P @R @Q @P curl F~ = − ~i + − ~j + − ~k: (1) @y @z @z @x @x @y Remarks: 1.
    [Show full text]
  • Multivariable and Vector Calculus
    Multivariable and Vector Calculus Lecture Notes for MATH 0200 (Spring 2015) Frederick Tsz-Ho Fong Department of Mathematics Brown University Contents 1 Three-Dimensional Space ....................................5 1.1 Rectangular Coordinates in R3 5 1.2 Dot Product7 1.3 Cross Product9 1.4 Lines and Planes 11 1.5 Parametric Curves 13 2 Partial Differentiations ....................................... 19 2.1 Functions of Several Variables 19 2.2 Partial Derivatives 22 2.3 Chain Rule 26 2.4 Directional Derivatives 30 2.5 Tangent Planes 34 2.6 Local Extrema 36 2.7 Lagrange’s Multiplier 41 2.8 Optimizations 46 3 Multiple Integrations ........................................ 49 3.1 Double Integrals in Rectangular Coordinates 49 3.2 Fubini’s Theorem for General Regions 53 3.3 Double Integrals in Polar Coordinates 57 3.4 Triple Integrals in Rectangular Coordinates 62 3.5 Triple Integrals in Cylindrical Coordinates 67 3.6 Triple Integrals in Spherical Coordinates 70 4 Vector Calculus ............................................ 75 4.1 Vector Fields on R2 and R3 75 4.2 Line Integrals of Vector Fields 83 4.3 Conservative Vector Fields 88 4.4 Green’s Theorem 98 4.5 Parametric Surfaces 105 4.6 Stokes’ Theorem 120 4.7 Divergence Theorem 127 5 Topics in Physics and Engineering .......................... 133 5.1 Coulomb’s Law 133 5.2 Introduction to Maxwell’s Equations 137 5.3 Heat Diffusion 141 5.4 Dirac Delta Functions 144 1 — Three-Dimensional Space 1.1 Rectangular Coordinates in R3 Throughout the course, we will use an ordered triple (x, y, z) to represent a point in the three dimensional space.
    [Show full text]
  • Deep Learning Based Computer Generated Face Identification Using
    applied sciences Article Deep Learning Based Computer Generated Face Identification Using Convolutional Neural Network L. Minh Dang 1, Syed Ibrahim Hassan 1, Suhyeon Im 1, Jaecheol Lee 2, Sujin Lee 1 and Hyeonjoon Moon 1,* 1 Department of Computer Science and Engineering, Sejong University, Seoul 143-747, Korea; [email protected] (L.M.D.); [email protected] (S.I.H.); [email protected] (S.I.); [email protected] (S.L.) 2 Department of Information Communication Engineering, Sungkyul University, Seoul 143-747, Korea; [email protected] * Correspondence: [email protected] Received: 30 October 2018; Accepted: 10 December 2018; Published: 13 December 2018 Abstract: Generative adversarial networks (GANs) describe an emerging generative model which has made impressive progress in the last few years in generating photorealistic facial images. As the result, it has become more and more difficult to differentiate between computer-generated and real face images, even with the human’s eyes. If the generated images are used with the intent to mislead and deceive readers, it would probably cause severe ethical, moral, and legal issues. Moreover, it is challenging to collect a dataset for computer-generated face identification that is large enough for research purposes because the number of realistic computer-generated images is still limited and scattered on the internet. Thus, a development of a novel decision support system for analyzing and detecting computer-generated face images generated by the GAN network is crucial. In this paper, we propose a customized convolutional neural network, namely CGFace, which is specifically designed for the computer-generated face detection task by customizing the number of convolutional layers, so it performs well in detecting computer-generated face images.
    [Show full text]
  • 9.2. Undoing the Chain Rule
    < Previous Section Home Next Section > 9.2. Undoing the Chain Rule This chapter focuses on finding accumulation functions in closed form when we know its rate of change function. We’ve seen that 1) an accumulation function in closed form is advantageous for quickly and easily generating many values of the accumulating quantity, and 2) the key to finding accumulation functions in closed form is the Fundamental Theorem of Calculus. The FTC says that an accumulation function is the antiderivative of the given rate of change function (because rate of change is the derivative of accumulation). In Chapter 6, we developed many derivative rules for quickly finding closed form rate of change functions from closed form accumulation functions. We also made a connection between the form of a rate of change function and the form of the accumulation function from which it was derived. Rather than inventing a whole new set of techniques for finding antiderivatives, our mindset as much as possible will be to use our derivatives rules in reverse to find antiderivatives. We worked hard to develop the derivative rules, so let’s keep using them to find antiderivatives! Thus, whenever you have a rate of change function f and are charged with finding its antiderivative, you should frame the task with the question “What function has f as its derivative?” For simple rate of change functions, this is easy, as long as you know your derivative rules well enough to apply them in reverse. For example, given a rate of change function …. … 2x, what function has 2x as its derivative? i.e.
    [Show full text]
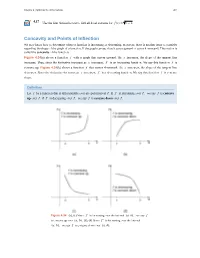
  • Concavity and Points of Inflection We Now Know How to Determine Where a Function Is Increasing Or Decreasing
    Chapter 4 | Applications of Derivatives 401 4.17 3 Use the first derivative test to find all local extrema for f (x) = x − 1. Concavity and Points of Inflection We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function. Figure 4.34(a) shows a function f with a graph that curves upward. As x increases, the slope of the tangent line increases. Thus, since the derivative increases as x increases, f ′ is an increasing function. We say this function f is concave up. Figure 4.34(b) shows a function f that curves downward. As x increases, the slope of the tangent line decreases. Since the derivative decreases as x increases, f ′ is a decreasing function. We say this function f is concave down. Definition Let f be a function that is differentiable over an open interval I. If f ′ is increasing over I, we say f is concave up over I. If f ′ is decreasing over I, we say f is concave down over I. Figure 4.34 (a), (c) Since f ′ is increasing over the interval (a, b), we say f is concave up over (a, b). (b), (d) Since f ′ is decreasing over the interval (a, b), we say f is concave down over (a, b). 402 Chapter 4 | Applications of Derivatives In general, without having the graph of a function f , how can we determine its concavity? By definition, a function f is concave up if f ′ is increasing.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Matrix Calculus
    Appendix D Matrix Calculus From too much study, and from extreme passion, cometh madnesse. Isaac Newton [205, §5] − D.1 Gradient, Directional derivative, Taylor series D.1.1 Gradients Gradient of a differentiable real function f(x) : RK R with respect to its vector argument is defined uniquely in terms of partial derivatives→ ∂f(x) ∂x1 ∂f(x) , ∂x2 RK f(x) . (2053) ∇ . ∈ . ∂f(x) ∂xK while the second-order gradient of the twice differentiable real function with respect to its vector argument is traditionally called the Hessian; 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂x1 ∂x1∂x2 ··· ∂x1∂xK 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 2 K f(x) , ∂x2∂x1 ∂x2 ··· ∂x2∂xK S (2054) ∇ . ∈ . .. 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂xK ∂x1 ∂xK ∂x2 ∂x ··· K interpreted ∂f(x) ∂f(x) 2 ∂ ∂ 2 ∂ f(x) ∂x1 ∂x2 ∂ f(x) = = = (2055) ∂x1∂x2 ³∂x2 ´ ³∂x1 ´ ∂x2∂x1 Dattorro, Convex Optimization Euclidean Distance Geometry, Mεβoo, 2005, v2020.02.29. 599 600 APPENDIX D. MATRIX CALCULUS The gradient of vector-valued function v(x) : R RN on real domain is a row vector → v(x) , ∂v1(x) ∂v2(x) ∂vN (x) RN (2056) ∇ ∂x ∂x ··· ∂x ∈ h i while the second-order gradient is 2 2 2 2 , ∂ v1(x) ∂ v2(x) ∂ vN (x) RN v(x) 2 2 2 (2057) ∇ ∂x ∂x ··· ∂x ∈ h i Gradient of vector-valued function h(x) : RK RN on vector domain is → ∂h1(x) ∂h2(x) ∂hN (x) ∂x1 ∂x1 ··· ∂x1 ∂h1(x) ∂h2(x) ∂hN (x) h(x) , ∂x2 ∂x2 ··· ∂x2 ∇ .
    [Show full text]
  • The Divergence of a Vector Field.Doc 1/8
    9/16/2005 The Divergence of a Vector Field.doc 1/8 The Divergence of a Vector Field The mathematical definition of divergence is: w∫∫ A(r )⋅ds ∇⋅A()rlim = S ∆→v 0 ∆v where the surface S is a closed surface that completely surrounds a very small volume ∆v at point r , and where ds points outward from the closed surface. From the definition of surface integral, we see that divergence basically indicates the amount of vector field A ()r that is converging to, or diverging from, a given point. For example, consider these vector fields in the region of a specific point: ∆ v ∆v ∇⋅A ()r0 < ∇ ⋅>A (r0) Jim Stiles The Univ. of Kansas Dept. of EECS 9/16/2005 The Divergence of a Vector Field.doc 2/8 The field on the left is converging to a point, and therefore the divergence of the vector field at that point is negative. Conversely, the vector field on the right is diverging from a point. As a result, the divergence of the vector field at that point is greater than zero. Consider some other vector fields in the region of a specific point: ∇⋅A ()r0 = ∇ ⋅=A (r0) For each of these vector fields, the surface integral is zero. Over some portions of the surface, the normal component is positive, whereas on other portions, the normal component is negative. However, integration over the entire surface is equal to zero—the divergence of the vector field at this point is zero. * Generally, the divergence of a vector field results in a scalar field (divergence) that is positive in some regions in space, negative other regions, and zero elsewhere.
    [Show full text]