DOCSLIB.ORG

Treewidth/Pathwidth

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Treewidth/Pathwidth Yonatan Itai March 2020 Treewidth/Pathwidth Seminar on Exact Exponential Algorithms • Definitions & motivation • Treewidth • Pathwidth • Dynamic programming examples on What are we graphs with bounded pathwidth going to talk • Maximum cut about? • Counting perfect matchings • Bounding a graph’s pathwidth • Independent set of size 푖 • Trees • Upper-bound in graphs of maximum degree 3 Why is the notion of treewidth/pathwidth interesting? • It is fundamental in graph theory and graph algorithms • Intuitively: measures the “similarity” of the graph to a tree/path • Multiple applications in exact algorithms on graphs • We can solve hard problems faster on graphs with bounded treewidth/pathwidth using dynamic programming Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Tree Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Tree Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Tree Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Tree Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Tree Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Tree Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Tree Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Tree Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Path Decomposition • The path decomposition of a graph is a tree decomposition with tree T being a path • A path decomposition is often denoted by listing the successive sets: • The width of a path decomposition is max • The pathwidth of a graph 퐺, denoted by 푝푤(퐺), is the minimum width of a path decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Path Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Nice Path Decomposition • A path decomposition (푋1, 푋2, … , 푋푟) of a graph 퐺 is nice if: • |푋1| = |푋푟| = 1 • For every 푖 ∈ {1,2, … , 푟 − 1} there is a vertex v of G such that either 푋푖+1 = 푋푖 ∪ {푣} or 푋푖+1 = 푋푖\{푣} • Given a path decomposition of a graph 퐺 of width 푘, a nice path decomposition of the same width can be constructed in a linear time Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Nice Path Decomposition Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Path Decomposition – Another Definition • Every vertex of the graph is an interval in ℝ • For every edge (푢, 푣) in the graph, there must be an intersection between the intervals of 푢 and 푣 The width is the maximum number of overlapping intervals minus 1 Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Path Decomposition – Another Definition A,B,C A,C,D C,D,E C,D,F F,G Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Path Decomposition – Another Definition A A,B A,B,C A,C A,C,D C,D C,D,E C,D C,D,F C,F FF F,G G Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut • The naïve solution – enumerate all possible cuts • There are 2푛 cuts, so the time complexity is 풪∗(2푛) • What about graphs with bounded pathwidth? Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut • We’re given a graph 퐺 and its path decomposition of width 푘 • Our goal: find a maximum cut in 풪∗(2푘) • More Formally: Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut • We can transform in linear time the given path decomposition to a nice path decomposition of width 푘: 푃 = (푋1, 푋2, … , 푋푟) • For 푖 ∈ {1,2, … , 푟}, we denote 푖 푉푖 = ራ 푋푗 푗=1 • Note that 푉푟 = 푉 Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut • We want to use dynamic programming • How can we partition our problem into smaller sub-problems? • Consider some 푋푖, and every partition of it into sets (퐴, 퐵) • We want to compute the maximum size of a cut in 퐺 푉푖 • The maximum is taken over all cuts (퐴′, 퐵′), s.t 퐴 ⊆ 퐴′ and 퐵 ⊆ 퐵′ • Denote it 푐푖(퐴, 퐵) • The maximum cut size in 퐺 is max{푐푟 퐴, 퐵 : 퐴, 퐵 is a partition of 푋푟} Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 푉푖 (A,B,C,D,E) 푋푖 A A,B A,B,C A,C A,C,D C,D C,D,E C,D C,D,F C,F FF F,G G D C E A B Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut • Our dynamic programming algorithm – for every 푖: • Compute 푐푖(퐴, 퐵) for every partition (퐴, 퐵) of 푋푖 • 푖 = 1: • 푋1 = 푣 for some 푣 ∈ 푉 • Only 2 possible partitions: (∅, 푣 ) and ( 푣 , ∅) • The size of a cut in both is 0 • 푖 > 1: We consider 2 cases • 푋푖 = 푋푖−1 ∪ 푣 for some 푣 ∈ 푉 • 푋푖 = 푋푖−1 \ 푣 for some 푣 ∈ 푉 Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut • 푋푖 = 푋푖−1 ∪ 푣 for some 푣 ∈ 푉 • We note that all neighbors of 푣 in 푉푖 are in 푋푖−1 ∩ 푋푖 = 푋푖−1 푉푖 푋1 푋2 푋푖−2 푋푖−1 푋푖 푋푟 푋푖−1 ∪ 푣 • Consider 푢, a neighbor of 푣 which is in 푉푖−1\X푖−1 • There exists 푗 < 푖 − 1 s.t 푢 ∈ 푋푗 • Also, as 푢, 푣 are neighbors, there must be a 푘 > 푖 s.t 푢 ∈ 푋푘 • But 푢 ∉ 푋푖−1, thus the sets containing it are not in the same connected sub-path Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 푉푖 (A,B,C,D,E) 푋푖 A A,B A,B,C A,C A,C,D C,D C,D,E C,D C,D,F C,F FF F,G G Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut • 푋푖 = 푋푖−1 ∪ 푣 for some 푣 ∈ 푉 • We note that all neighbors of 푣 in 푉푖 are in 푋푖−1 ∩ 푋푖 = 푋푖−1 • Then for every partition (퐴, 퐵) of 푋푖 푐푖−1(퐴\ {푣}, 퐵) + 퐶푈푇({푣}, 퐵), if 푣 ∈ 퐴 푐푖(퐴, 퐵) = ቊ 푐푖−1 퐴, 퐵\ 푣 + 퐶푈푇 푣 , 퐴 , if 푣 ∉ 퐴 Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 푉푖 (A,B,C,D,E) 푋푖 A A,B A,B,C A,C A,C,D C,D C,D,E C,D C,D,F C,F FF F,G G D C E B A Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut • 푋푖 = 푋푖−1\ 푣 for some 푣 ∈ 푉 • We notice that in this case 푉푖 = 푉푖−1 • For every partition (퐴, 퐵) of 푋푖 • 푋푖−1 has 2 partitions that “respect” (퐴, 퐵) • Hence: 푐푖 퐴, 퐵 = max{푐푖−1 퐴 ∪ 푣 , 퐵 , 푐푖−1(퐴, 퐵 ∪ 푣 ) Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 푉푖 (A,B,C,D,E) 푋푖 A A,B A,B,C A,C A,C,D C,D C,D,E C,D C,D,F C,F FF F,G G D C E Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Maximum Cut – Complexity • For every 푖 ∈ {1, … , 푟} 푋푖 • There are 2 partitions (퐴, 퐵) of 푋푖 • 푐푖(퐴, 퐵) can be computed in 풪 |푋푖| • We store the computation for every partition (we need the computatioms for 푖 − 1 when we do the computations for 푖) • Total running time: 푟 푋푖 푘 ∗ 푘 풪 ෍ 2 |푋푖| = 풪 2 ⋅ 푘 ⋅ 푛 = 풪 (2 ) 푖=1 • Total space used: 풪∗ 2푘 Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Counting Perfect Matchings • Reminder – we talked last week about perfect matchings in bipartite graphs • A matching 푀 of a graph 퐺 = 푉, 퐸 is perfect if 푀 is an edge cover of 퐺 1 a 2 b 3 c 4 d Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Counting Perfect Matchings • Example of a perfect matching in non-bipartite graph: Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Counting Perfect Matchings • For bipartite graphs – inclusion/exclusion algorithm • Time: 풪∗ 2푛 • Space: Polynomial • We haven’t seen an algorithm for the general case • We can use dynamic programming algorithm to count perfect matchings in a general graph with bounded pathwidth: Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Counting Perfect Matchings • We can transform in linear time the given path decomposition to a nice path decomposition of width 푘: 푃 = (푋1, 푋2, … , 푋푟) • For 푖 ∈ {1,2, … , 푟}, we denote 푖 푉푖 = ራ 푋푗 푗=1 • Note that 푉푟 = 푉 Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Counting Perfect Matchings • Consider some 푋푖, and every partition of it into sets (퐴, 퐵) • We’ll compute the number of matchings 푀 in 퐺 푉푖 such that: • 푀 covers every vertex of 푉푖 \B • 푀 doesn’t cover any of the vertices of 퐵 • Denote it 푚푖(퐴, 퐵) • The number of perfect matchings in 퐺 is 푚푟 푋푟, ∅ Definitions & Counting perfect Bounding Pathwidth when Maximum Cut motivation matchings pathwidth Δ = 3 Counting Perfect Matchings • Our dynamic programming algorithm – for every 푖: • Compute 푚푖(퐴, 퐵) for every partition (퐴, 퐵) of 푋푖 • 푖 = 1: • 푋1 = 푣 for some 푣 ∈ 푉 • Only
Load more

Recommended publications
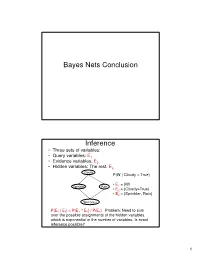
  • Bayes Nets Conclusion Inference
    Bayes Nets Conclusion Inference • Three sets of variables: • Query variables: E1 • Evidence variables: E2 • Hidden variables: The rest, E3 Cloudy P(W | Cloudy = True) • E = {W} Sprinkler Rain 1 • E2 = {Cloudy=True} • E3 = {Sprinkler, Rain} Wet Grass P(E 1 | E 2) = P(E 1 ^ E 2) / P(E 2) Problem: Need to sum over the possible assignments of the hidden variables, which is exponential in the number of variables. Is exact inference possible? 1 A Simple Case A B C D • Suppose that we want to compute P(D = d) from this network. A Simple Case A B C D • Compute P(D = d) by summing the joint probability over all possible values of the remaining variables A, B, and C: P(D === d) === ∑∑∑ P(A === a, B === b,C === c, D === d) a,b,c 2 A Simple Case A B C D • Decompose the joint by using the fact that it is the product of terms of the form: P(X | Parents(X)) P(D === d) === ∑∑∑ P(D === d | C === c)P(C === c | B === b)P(B === b | A === a)P(A === a) a,b,c A Simple Case A B C D • We can avoid computing the sum for all possible triplets ( A,B,C) by distributing the sums inside the product P(D === d) === ∑∑∑ P(D === d | C === c)∑∑∑P(C === c | B === b)∑∑∑P(B === b| A === a)P(A === a) c b a 3 A Simple Case A B C D This term depends only on B and can be written as a 2- valued function fA(b) P(D === d) === ∑∑∑ P(D === d | C === c)∑∑∑P(C === c | B === b)∑∑∑P(B === b| A === a)P(A === a) c b a A Simple Case A B C D This term depends only on c and can be written as a 2- valued function fB(c) === === === === === === P(D d) ∑∑∑ P(D d | C c)∑∑∑P(C c | B b)f A(b) c b ….
    [Show full text]
  • On Treewidth and Graph Minors
    On Treewidth and Graph Minors Daniel John Harvey Submitted in total fulfilment of the requirements of the degree of Doctor of Philosophy February 2014 Department of Mathematics and Statistics The University of Melbourne Produced on archival quality paper ii Abstract Both treewidth and the Hadwiger number are key graph parameters in structural and al- gorithmic graph theory, especially in the theory of graph minors. For example, treewidth demarcates the two major cases of the Robertson and Seymour proof of Wagner's Con- jecture. Also, the Hadwiger number is the key measure of the structural complexity of a graph. In this thesis, we shall investigate these parameters on some interesting classes of graphs. The treewidth of a graph defines, in some sense, how \tree-like" the graph is. Treewidth is a key parameter in the algorithmic field of fixed-parameter tractability. In particular, on classes of bounded treewidth, certain NP-Hard problems can be solved in polynomial time. In structural graph theory, treewidth is of key interest due to its part in the stronger form of Robertson and Seymour's Graph Minor Structure Theorem. A key fact is that the treewidth of a graph is tied to the size of its largest grid minor. In fact, treewidth is tied to a large number of other graph structural parameters, which this thesis thoroughly investigates. In doing so, some of the tying functions between these results are improved. This thesis also determines exactly the treewidth of the line graph of a complete graph. This is a critical example in a recent paper of Marx, and improves on a recent result by Grohe and Marx.
    [Show full text]
  • Treewidth I (Algorithms and Networks)
    Treewidth Algorithms and Networks Overview • Historic introduction: Series parallel graphs • Dynamic programming on trees • Dynamic programming on series parallel graphs • Treewidth • Dynamic programming on graphs of small treewidth • Finding tree decompositions 2 Treewidth Computing the Resistance With the Laws of Ohm = + 1 1 1 1789-1854 R R1 R2 = + R R1 R2 R1 R2 R1 Two resistors in series R2 Two resistors in parallel 3 Treewidth Repeated use of the rules 6 6 5 2 2 1 7 Has resistance 4 1/6 + 1/2 = 1/(1.5) 1.5 + 1.5 + 5 = 8 1 + 7 = 8 1/8 + 1/8 = 1/4 4 Treewidth 5 6 6 5 2 2 1 7 A tree structure tree A 5 6 P S 2 P 6 P 2 7 S Treewidth 1 Carry on! • Internal structure of 6 6 5 graph can be forgotten 2 2 once we know essential information 1 7 about it! 4 ¼ + ¼ = ½ 6 Treewidth Using tree structures for solving hard problems on graphs 1 • Network is ‘series parallel graph’ • 196*, 197*: many problems that are hard for general graphs are easy for e.g.: – Trees NP-complete – Series parallel graphs • Many well-known problems Linear / polynomial time computable 7 Treewidth Weighted Independent Set • Independent set: set of vertices that are pair wise non-adjacent. • Weighted independent set – Given: Graph G=(V,E), weight w(v) for each vertex v. – Question: What is the maximum total weight of an independent set in G? • NP-complete 8 Treewidth Weighted Independent Set on Trees • On trees, this problem can be solved in linear time with dynamic programming.
    [Show full text]
  • Counting Independent Sets in Graphs with Bounded Bipartite Pathwidth∗
    Counting independent sets in graphs with bounded bipartite pathwidth∗ Martin Dyery Catherine Greenhillz School of Computing School of Mathematics and Statistics University of Leeds UNSW Sydney, NSW 2052 Leeds LS2 9JT, UK Australia [email protected] [email protected] Haiko M¨uller∗ School of Computing University of Leeds Leeds LS2 9JT, UK [email protected] 7 August 2019 Abstract We show that a simple Markov chain, the Glauber dynamics, can efficiently sample independent sets almost uniformly at random in polynomial time for graphs in a certain class. The class is determined by boundedness of a new graph parameter called bipartite pathwidth. This result, which we prove for the more general hardcore distribution with fugacity λ, can be viewed as a strong generalisation of Jerrum and Sinclair's work on approximately counting matchings, that is, independent sets in line graphs. The class of graphs with bounded bipartite pathwidth includes claw-free graphs, which generalise line graphs. We consider two further generalisations of claw-free graphs and prove that these classes have bounded bipartite pathwidth. We also show how to extend all our results to polynomially-bounded vertex weights. 1 Introduction There is a well-known bijection between matchings of a graph G and independent sets in the line graph of G. We will show that we can approximate the number of independent sets ∗A preliminary version of this paper appeared as [19]. yResearch supported by EPSRC grant EP/S016562/1 \Sampling in hereditary classes". zResearch supported by Australian Research Council grant DP190100977. 1 in graphs for which all bipartite induced subgraphs are well structured, in a sense that we will define precisely.
    [Show full text]
  • Randomly Coloring Graphs of Logarithmically Bounded Pathwidth Shai Vardi
    Randomly coloring graphs of logarithmically bounded pathwidth Shai Vardi To cite this version: Shai Vardi. Randomly coloring graphs of logarithmically bounded pathwidth. 2018. hal-01832102 HAL Id: hal-01832102 https://hal.archives-ouvertes.fr/hal-01832102 Preprint submitted on 6 Jul 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Randomly coloring graphs of logarithmically bounded pathwidth Shai Vardi∗ Abstract We consider the problem of sampling a proper k-coloring of a graph of maximal degree ∆ uniformly at random. We describe a new Markov chain for sampling colorings, and show that it mixes rapidly on graphs of logarithmically bounded pathwidth if k ≥ (1 + )∆, for any > 0, using a new hybrid paths argument. ∗California Institute of Technology, Pasadena, CA, 91125, USA. E-mail: [email protected]. 1 Introduction A (proper) k-coloring of a graph G = (V; E) is an assignment σ : V ! f1; : : : ; kg such that neighboring vertices have different colors. We consider the problem of sampling (almost) uniformly at random from the space of all k-colorings of a graph.1 The problem has received considerable attention from the computer science community in recent years, e.g., [12, 17, 24, 26, 33, 44, 45].
    [Show full text]
  • Network Analysis of the Multimodal Freight Transportation System in New York City
    Network Analysis of the Multimodal Freight Transportation System in New York City Project Number: 15 – 2.1b Year: 2015 FINAL REPORT June 2018 Principal Investigator Qian Wang Researcher Shuai Tang MetroFreight Center of Excellence University at Buffalo Buffalo, NY 14260-4300 Network Analysis of the Multimodal Freight Transportation System in New York City ABSTRACT The research is aimed at examining the multimodal freight transportation network in the New York metropolitan region to identify critical links, nodes and terminals that affect last-mile deliveries. Two types of analysis were conducted to gain a big picture of the region’s freight transportation network. First, three categories of network measures were generated for the highway network that carries the majority of last-mile deliveries. They are the descriptive measures that demonstrate the basic characteristics of the highway network, the network structure measures that quantify the connectivity of nodes and links, and the accessibility indices that measure the ease to access freight demand, services and activities. Second, 71 multimodal freight terminals were selected and evaluated in terms of their accessibility to major multimodal freight demand generators such as warehousing establishments. As found, the most important highways nodes that are critical in terms of connectivity and accessibility are those in and around Manhattan, particularly the bridges and tunnels connecting Manhattan to neighboring areas. Major multimodal freight demand generators, such as warehousing establishments, have better accessibility to railroad and marine port terminals than air and truck terminals in general. The network measures and findings in the research can be used to understand the inventory of the freight network in the system and to conduct freight travel demand forecasting analysis.
    [Show full text]
  • Density Theorems for Bipartite Graphs and Related Ramsey-Type Results
    Density theorems for bipartite graphs and related Ramsey-type results Jacob Fox Benny Sudakov Princeton UCLA and IAS Ramsey’s theorem Definition: r(G) is the minimum N such that every 2-edge-coloring of the complete graph KN contains a monochromatic copy of graph G. Theorem: (Ramsey-Erdos-Szekeres,˝ Erdos)˝ t/2 2t 2 ≤ r(Kt ) ≤ 2 . Question: (Burr-Erd˝os1975) How large is r(G) for a sparse graph G on n vertices? Ramsey numbers for sparse graphs Conjecture: (Burr-Erd˝os1975) For every d there exists a constant cd such that if a graph G has n vertices and maximum degree d, then r(G) ≤ cd n. Theorem: 1 (Chv´atal-R¨odl-Szemer´edi-Trotter 1983) cd exists. 2αd 2 (Eaton 1998) cd ≤ 2 . βd αd log2 d 3 (Graham-R¨odl-Ruci´nski2000) 2 ≤ cd ≤ 2 . Moreover, if G is bipartite, r(G) ≤ 2αd log d n. Density theorem for bipartite graphs Theorem: (F.-Sudakov) Let G be a bipartite graph with n vertices and maximum degree d 2 and let H be a bipartite graph with parts |V1| = |V2| = N and εN edges. If N ≥ 8dε−d n, then H contains G. Corollary: For every bipartite graph G with n vertices and maximum degree d, r(G) ≤ d2d+4n. (D. Conlon independently proved that r(G) ≤ 2(2+o(1))d n.) Proof: Take ε = 1/2 and H to be the graph of the majority color. Ramsey numbers for cubes Definition: d The binary cube Qd has vertex set {0, 1} and x, y are adjacent if x and y differ in exactly one coordinate.
    [Show full text]
  • Constrained Representations of Map Graphs and Half-Squares
    Constrained Representations of Map Graphs and Half-Squares Hoang-Oanh Le Berlin, Germany [email protected] Van Bang Le Universität Rostock, Institut für Informatik, Rostock, Germany [email protected] Abstract The square of a graph H, denoted H2, is obtained from H by adding new edges between two distinct vertices whenever their distance in H is two. The half-squares of a bipartite graph B = (X, Y, EB ) are the subgraphs of B2 induced by the color classes X and Y , B2[X] and B2[Y ]. For a given graph 2 G = (V, EG), if G = B [V ] for some bipartite graph B = (V, W, EB ), then B is a representation of G and W is the set of points in B. If in addition B is planar, then G is also called a map graph and B is a witness of G [Chen, Grigni, Papadimitriou. Map graphs. J. ACM, 49 (2) (2002) 127-138]. While Chen, Grigni, Papadimitriou proved that any map graph G = (V, EG) has a witness with at most 3|V | − 6 points, we show that, given a map graph G and an integer k, deciding if G admits a witness with at most k points is NP-complete. As a by-product, we obtain NP-completeness of edge clique partition on planar graphs; until this present paper, the complexity status of edge clique partition for planar graphs was previously unknown. We also consider half-squares of tree-convex bipartite graphs and prove the following complexity 2 dichotomy: Given a graph G = (V, EG) and an integer k, deciding if G = B [V ] for some tree-convex bipartite graph B = (V, W, EB ) with |W | ≤ k points is NP-complete if G is non-chordal dually chordal and solvable in linear time otherwise.
    [Show full text]
  • Tree Structures
    Tree Structures Definitions: o A tree is a connected acyclic graph. o A disconnected acyclic graph is called a forest o A tree is a connected digraph with these properties: . There is exactly one node (Root) with in-degree=0 . All other nodes have in-degree=1 . A leaf is a node with out-degree=0 . There is exactly one path from the root to any leaf o The degree of a tree is the maximum out-degree of the nodes in the tree. o If (X,Y) is a path: X is an ancestor of Y, and Y is a descendant of X. Root X Y CSci 1112 – Algorithms and Data Structures, A. Bellaachia Page 1 Level of a node: Level 0 or 1 1 or 2 2 or 3 3 or 4 Height or depth: o The depth of a node is the number of edges from the root to the node. o The root node has depth zero o The height of a node is the number of edges from the node to the deepest leaf. o The height of a tree is a height of the root. o The height of the root is the height of the tree o Leaf nodes have height zero o A tree with only a single node (hence both a root and leaf) has depth and height zero. o An empty tree (tree with no nodes) has depth and height −1. o It is the maximum level of any node in the tree. CSci 1112 – Algorithms and Data Structures, A.
    [Show full text]
  • A Simple Linear-Time Algorithm for Finding Path-Decompostions of Small Width
    Introduction Preliminary Definitions Pathwidth Algorithm Summary A Simple Linear-Time Algorithm for Finding Path-Decompostions of Small Width Kevin Cattell Michael J. Dinneen Michael R. Fellows Department of Computer Science University of Victoria Victoria, B.C. Canada V8W 3P6 Information Processing Letters 57 (1996) 197–203 Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Pathwidth Algorithm Summary Outline 1 Introduction Motivation History 2 Preliminary Definitions Boundaried graphs Path-decompositions Topological tree obstructions 3 Pathwidth Algorithm Main result Linear-time algorithm Proof of correctness Other results Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Motivation Pathwidth Algorithm History Summary Motivation Pathwidth is related to several VLSI layout problems: vertex separation link gate matrix layout edge search number ... Usefullness of bounded treewidth in: study of graph minors (Robertson and Seymour) input restrictions for many NP-complete problems (fixed-parameter complexity) Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Motivation Pathwidth Algorithm History Summary History General problem(s) is NP-complete Input: Graph G, integer t Question: Is tree/path-width(G) ≤ t? Algorithmic development (fixed t): O(n2) nonconstructive treewidth algorithm by Robertson and Seymour (1986) O(nt+2) treewidth algorithm due to Arnberg, Corneil and Proskurowski (1987) O(n log n) treewidth algorithm due to Reed (1992) 2 O(2t n) treewidth algorithm due to Bodlaender (1993) O(n log2 n) pathwidth algorithm due to Ellis, Sudborough and Turner (1994) Kevin Cattell, Michael J. Dinneen, Michael R.
    [Show full text]
  • Minimal Acyclic Forbidden Minors for the Family of Graphs with Bounded Path-Width
    Discrete Mathematics 127 (1994) 293-304 293 North-Holland Minimal acyclic forbidden minors for the family of graphs with bounded path-width Atsushi Takahashi, Shuichi Ueno and Yoji Kajitani Department of Electrical and Electronic Engineering, Tokyo Institute of Technology. Tokyo, 152. Japan Received 27 November 1990 Revised 12 February 1992 Abstract The graphs with bounded path-width, introduced by Robertson and Seymour, and the graphs with bounded proper-path-width, introduced in this paper, are investigated. These families of graphs are minor-closed. We characterize the minimal acyclic forbidden minors for these families of graphs. We also give estimates for the numbers of minimal forbidden minors and for the numbers of vertices of the largest minimal forbidden minors for these families of graphs. 1. Introduction Graphs we consider are finite and undirected, but may have loops and multiple edges unless otherwise specified. A graph H is a minor of a graph G if H is isomorphic to a graph obtained from a subgraph of G by contracting edges. A family 9 of graphs is said to be minor-closed if the following condition holds: If GEB and H is a minor of G then H EF. A graph G is a minimal forbidden minor for a minor-closed family F of graphs if G#8 and any proper minor of G is in 9. Robertson and Seymour proved the following deep theorems. Theorem 1.1 (Robertson and Seymour [15]). Every minor-closed family of graphs has a finite number of minimal forbidden minors. Theorem 1.2 (Robertson and Seymour [14]).
    [Show full text]
  • Arxiv:2006.06067V2 [Math.CO] 4 Jul 2021
    Treewidth versus clique number. I. Graph classes with a forbidden structure∗† Cl´ement Dallard1 Martin Milaniˇc1 Kenny Storgelˇ 2 1 FAMNIT and IAM, University of Primorska, Koper, Slovenia 2 Faculty of Information Studies, Novo mesto, Slovenia [email protected] [email protected] [email protected] Treewidth is an important graph invariant, relevant for both structural and algo- rithmic reasons. A necessary condition for a graph class to have bounded treewidth is the absence of large cliques. We study graph classes closed under taking induced subgraphs in which this condition is also sufficient, which we call (tw,ω)-bounded. Such graph classes are known to have useful algorithmic applications related to variants of the clique and k-coloring problems. We consider six well-known graph containment relations: the minor, topological minor, subgraph, induced minor, in- duced topological minor, and induced subgraph relations. For each of them, we give a complete characterization of the graphs H for which the class of graphs excluding H is (tw,ω)-bounded. Our results yield an infinite family of χ-bounded induced-minor-closed graph classes and imply that the class of 1-perfectly orientable graphs is (tw,ω)-bounded, leading to linear-time algorithms for k-coloring 1-perfectly orientable graphs for every fixed k. This answers a question of Breˇsar, Hartinger, Kos, and Milaniˇc from 2018, and one of Beisegel, Chudnovsky, Gurvich, Milaniˇc, and Servatius from 2019, respectively. We also reveal some further algorithmic implications of (tw,ω)- boundedness related to list k-coloring and clique problems. In addition, we propose a question about the complexity of the Maximum Weight Independent Set prob- lem in (tw,ω)-bounded graph classes and prove that the problem is polynomial-time solvable in every class of graphs excluding a fixed star as an induced minor.
    [Show full text]