Eclipse Cycles, and Can Be Computed from the Numerical Results of the Preceding Paragraphs; Cf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Illuminating Eclipses: Astronomy and Chronology in King Lear
Brief Chronicles Vol. II (2010) 32 Illuminating Eclipses: Astronomy and Chronology in King Lear Hanno Wember ohann Gottfried Herder wrote his famous essay Shakespeare in 1772. He was (as Wieland, Lessing and, of course, Goethe and Schiller) one of the 18th century German writers “who first embraced Shakespeare and welcomed his Jgenius as a dramatist.”1 In his 1980 introduction to Herder’s essay, Konrad Nussbächer wrote: “Shakespeare is not, as it appeared in the 18th century, a natural genius growing up in the wild, but a highly cultured, artful Renaissance poet and practitioner of the stage.” Astronomy was one of the liberal arts and sciences a “highly cultured” man of Renaissance England was expected to know. This essay will review a few illuminating examples of Shakespeare’s profound knowledge of astronomy, and will examine a new astronomical reference that could shed significant new light on Shakespearean chronology. Shakespeare’s Astronomy In many regards Shakespeare had a better knowledge of the relationship between the moon and the tides2 than his distinguished contemporary Galileo (1564 - 1642), who tried to explain the tides by the two motions of the earth, correlating to the day and the year.3 This was an erroneous explanation for ebb and flow. But while Galileo refused to acknowledge any tidal influence of the moon, Bernardo knew better, referring to the moon as the Brief Chronicles Vol. II (2010) 33 moist star Upon whose influence Neptune’s empire stands (Hamlet, I.1.135)4 To Prince Henry, likewise, the moon commands the tides: The fortune of us that are moon’s men doth ebb and flow like the sea, being governed as the sea is by the moon…..Now in as low an ebb as the foot of the ladder, and by and by in as high a flow as the ridge of the gallows. -
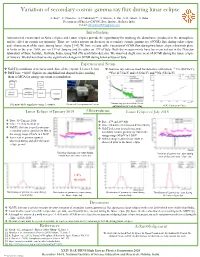
Variation of Secondary Cosmic Gamma Ray Flux During Lunar Eclipse
Variation of secondary cosmic gamma ray flux during lunar eclipse S. Roy* , S. Chatterjee , S. Chakraborty** , S. Biswas , S. Das , S. K. Ghosh , S. Raha Department of Physics (CAPSS), Bose Institute, Kolkata, India. E-mail: [email protected] Introduction Astronomical events such as Solar eclipses and Lunar eclipses provide the opportunity for studying the disturbance produced in the atmosphere and its effect on cosmic ray intensity. There are earlier reports on decrease in secondary cosmic gamma ray (SCGR) flux during solar eclipse and enhancement of the same during lunar eclipse [1-4]. We have measured the variation of SCGR flux during two lunar eclipses that took place in India in the year 2018, one on 31st of January and the other on 27th of July. Both the measurements have been carried out in the Detector laboratory of Bose Institute, Kolkata, India, using NaI (Tl) scintillator detector. We observed slight increment of SCGR during the lunar eclipse of January. We did not observe any significant changes in SCGR during lunar eclipse of July. Experimental Setup ❖ NaI(Tl) scintillator detector is used. Size of the crystal: 5.1cm × 5.1cm ❖ Gamma ray sources used for detector calibration: 137Cs (662 keV), ❖ PMT bias: +600V. Signals are amplified and shaped before sending 60Co (1173 keV and 1332 keV) and 22Na (551 keV) them to MCA for energy spectrum accumulation ORTEC-556 ORTEC-671 Schematic of the signal processing electronics Picture of the experimental setup Gamma ray spectra with different configurations of lead shielding ADC -

Alexander Jones Calendrica I: New Callippic Dates
ALEXANDER JONES CALENDRICA I: NEW CALLIPPIC DATES aus: Zeitschrift für Papyrologie und Epigraphik 129 (2000) 141–158 © Dr. Rudolf Habelt GmbH, Bonn 141 CALENDRICA I: NEW CALLIPPIC DATES 1. Introduction. Callippic dates are familiar to students of Greek chronology, even though up to the present they have been known to occur only in a single source, Ptolemy’s Almagest (c. A.D. 150).1 Ptolemy’s Callippic dates appear in the context of discussions of astronomical observations ranging from the early third century B.C. to the third quarter of the second century B.C. In the present article I will present new attestations of Callippic dates which extend the period of the known use of this system by almost two centuries, into the middle of the first century A.D. I also take the opportunity to attempt a fresh examination of what we can deduce about the Callippic calendar and its history, a topic that has lately been the subject of quite divergent treatments. The distinguishing mark of a Callippic date is the specification of the year by a numbered “period according to Callippus” and a year number within that period. Each Callippic period comprised 76 years, and year 1 of Callippic Period 1 began about midsummer of 330 B.C. It is an obvious, and very reasonable, supposition that this convention for counting years was instituted by Callippus, the fourth- century astronomer whose revisions of Eudoxus’ planetary theory are mentioned by Aristotle in Metaphysics Λ 1073b32–38, and who also is prominent among the authorities cited in astronomical weather calendars (parapegmata).2 The point of the cycles is that 76 years contain exactly four so-called Metonic cycles of 19 years. -

Viewing an Eclipse Safely
ECLIPSES SOLAR an eclipse safely How to observe SOLAR ECLIPSE, OCTOBER 2014, BY LEMAN NORTHWAY Solar eclipses are quite rare and are often a major event. The SOLAR ECLIPSES Moon passes right in front of the Sun, blotting out its disc. Every time a solar eclipse occurs there are various things to look for. However, it is extremely dangerous to just go out and look up. The Sun is so bright that just looking at it can blind you, so you’ll need to prepare beforehand. There are various ways to observe eclipses safely, using both everyday materials and telescopes or binoculars. So read this leaflet Introduction to find out what happens during an eclipse and how you can see all the stages of the event safely. This booklet was written by the Royal Astronomical Society with The Society for Popular Astronomy and is endorsed by the British Astronomical Association The Royal Astronomical The Society for Popular Formed in 1890, the Society, founded in Astronomy is for British Astronomical 1820, encourages and beginners of all ages. Our Association has an promotes the study of aim is to make astronomy international reputation astronomy, solar-system fun, and our magazine, for the quality of science, geophysics and Popular Astronomy, is full its observational closely related branches of information to help and scientific work. of science. you get to know the Membership is open to www.ras.org.uk sky and get involved. We even have a special Young all persons interested in HIGGS-BOSON.COM JOHNSON: PAUL BY D Stargazers section, run by TV’s Lucie Green. -

I. ASYMMETRY of ECLIPSES. CALENDAR CYCLES Igor Taganov & Ville-V.E
I. ASYMMETRY OF ECLIPSES. CALENDAR CYCLES Igor Taganov & Ville-V.E. Saari 1.1 Metaphysics of solar eclipses p. 12 1.2 Calendar cycles of solar eclipses p. 20 Literature p. 26 To describe the two main types of solar eclipses in modern astronomy the old Latin terms – umbra, antumbra and penumbra are still used (Fig. 1.1). A “partial eclipse” (c. 35 %) occurs when the Sun and Moon are not exactly in line and the Moon only partially obscures the Sun. The term “central eclipse” (c. 65 %) is often used as a generic term for eclipses when the Sun and Moon are exactly in line. The strict definition of a central eclipse is an eclipse, during which the central line of the Moon’s umbra touches the Earth’s surface. However, extremely rare the part of the Moon’s umbra intersects with Earth, producing an annular or total eclipse, but not its central line. Such event is called a “non-central” total or annular eclipse [2]. Fig. 1.1. Main types of solar eclipses The central solar eclipses are subdivided into three main groups: a “total eclipse” (c. 27 %) occurs when the dark silhouette of the Moon completely obscures the Sun; an “annular eclipse” (c. 33 %) occurs when the Sun and Moon are exactly in line, but the apparent size of the Moon is smaller than that of the Sun; a “hybrid eclipse” or annular/total eclipse (c. 5 %) at certain sites on the Earth’s surface appears as a total eclipse, whereas at other sites it looks as annular. -

Roll 5, Side A
doi: 10.1038/nature07130 SUPPLEMENTARY INFORMATION Correction notice Calendars with Olympiad display and eclipse prediction on the Antikythera Mechanism Tony Freeth, Alexander Jones, John M. Steele & Yanis Bitsakis Nature 454, 614–617 (2008) In the version of the Supplementary Information originally posted online, there were minor errors in Supplementary Figs 20 and 25. In Supplementary Fig. 20, some glyphs were accidently omitted between months 26 and 67; in Supplementary Fig. 25, seven glyphs in the left-hand semicircle were inscribed one month too early. These have been corrected in the new version of the Supplementary Information; see Supplementary Information Table of Contents for details. doi: 10.1038/nature07130 SUPPLEMENTARY INFORMATION Calendars with Olympiad display and eclipse prediction on the Antikythera Mechanism SUPPLEMENTARY NOTES Tony Freeth1,2, Alexander Jones3, John M. Steele4 & Yanis Bitsakis1,5 1 Antikythera Mechanism Research Project, 3 Tyrwhitt Crescent, Roath Park, Cardiff CF23 5QP, UK. 2 Images First Ltd, 10 Hereford Road, South Ealing, London W5 4SE, UK. 3 Institute for the Study of the Ancient World, 15 East 84th Street, New York, NY 10028, USA. 4 Department of Physics, University of Durham, Rochester Building, South Road, Durham DH1 3LE, UK. 5 Centre for History and Palaeography, 3, P. Skouze str., GR-10560 Athens, Greece www.nature.com/nature doi: 10.1038/nature07130 SUPPLEMENTARY INFORMATION Calendars with Olympiad display and eclipse prediction on the Antikythera Mechanism Supplementary Notes Table of Contents TABLE OF CONTENTS 1. OVERVIEW OF THE ANTIKYTHERA MECHANISM 1 1.1 The Fragments 1 1.2 The Architecture of the Mechanism 1 2. DATA ACQUISITION & ANALYSIS 4 2.1 Data Acquisition 4 2.2 Data Analysis 5 3. -

1986Aj 92.120Id the Astronomical Journal Volume 92, Number 5 November 1986 Modeling Pluto-Charon Mutual Eclipse Events. I. First
THE ASTRONOMICAL JOURNAL VOLUME 92, NUMBER 5 NOVEMBER 1986 92.120ID MODELING PLUTO-CHARON MUTUAL ECLIPSE EVENTS. I. FIRST-ORDER MODELS R. Scott Dunbar and Edward F. Tedesco Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California 91109 1986AJ Received 29 May 1986; revised 7August 1986 ABSTRACT We present numerical and analytical models describing the light curves resulting from mutual events between close planetary binaries, with particular application to the Pluto-Charon system. These models are referred to as “first-order” models because they incorporate the effects of shadowing in such sys- tems, in contrast to “zeroth-order” models, which do not include shadowing. The shadows cast between close binaries of similar size (as in the case of Pluto and Charon) can be treated as extensions of the eclipsing bodies themselves at small solar phase angles. Shadowing plays a major role in the morphology of mutual event light curves. The numerical approach is a straightforward, but computationally inten- sive, discrete-element integration. The analytical approach uses a conceptually simple model of three circular disks, representing the planet, satellite, and shadow, and computes the complex geometric relationship among these three disks to obtain the eclipse magnitude at each time step. The results of the two models agree to well within the expected light-curve measurement error. A preliminary model fit to the depths of five mutual eclipse events observed in 1985 and 1986 gives eclipse light-curve-derived estimates of the orbit radius C = 16.5 + 0.5 Pluto radii, the radius ratio B0 = 0.65 + 0.03, and the Charon:Pluto albedo ratio K — 0.55 + 0.15. -

94 Erkka Maula
ORGANON 15 PROBLÊMES GENERAUX Erkka Maula (Finland) FROM TIME TO PLACE: THE PARADIGM CASE The world-order in philosophical cosmology can be founded upon time as well as .space. Perhaps the most fundamental question pertaining to any articulated world- view concerns, accordingly, their ontological and epistemological priority. Is the basic layer of notions characterized by temporal or by spatial concepts? Does a world-view in its development show tendencies toward the predominance of one set of concepts rather than the other? At the stage of its relative maturity, when the qualitative and comparative phases have paved the way for the formation of quantitative concepts: Which are considered more fundamental, measurements of time or measurements of space? In the comparative phase: Is the geometry of the world a geometry of motion or a geometry of timeless order? In the history of our own scientific world-view, there seems to be discernible an oscillation between time-oriented and space-oriented concept formation.1 In the dawn, when the first mathematical systems of astronomy and geography appear, shortly before Euclid's synthesis of the axiomatic thought, there were attempts at a geometry of motion. They are due to Archytas of Tarentum and Eudoxus of Cnidus, foreshadowed by Hippias of Elis and the Pythagoreans, who tend to intro- duce temporal concepts into geometry. Their most eloquent adversary is Plato, and after him the two alternative streams are often called the Heraclitean and the Parmenidean world-views. But also such later and far more articulated distinctions as those between the statical and dynamic cosmologies, or between the formalist and intuitionist philosophies of mathematics, can be traced down to the original Greek dichotomy, although additional concepts entangle the picture. -

Geminos and Babylonian Astronomy
Geminos and Babylonian astronomy J. M. Steele Introduction Geminos’ Introduction to the Phenomena is one of several introductions to astronomy written by Greek and Latin authors during the last couple of centuries bc and the first few centuries ad.1 Geminos’ work is unusual, however, in including some fairly detailed—and accurate—technical information about Babylonian astronomy, some of which is explicitly attributed to the “Chal- deans.” Indeed, before the rediscovery of cuneiform sources in the nineteenth century, Gem- inos provided the most detailed information on Babylonian astronomy available, aside from the reports of several eclipse and planetary observations quoted by Ptolemy in the Almagest. Early-modern histories of astronomy, those that did not simply quote fantastical accounts of pre-Greek astronomy based upon the Bible and Josephus, relied heavily upon Geminos for their discussion of Babylonian (or “Chaldean”) astronomy.2 What can be learnt of Babylonian astron- omy from Geminos is, of course, extremely limited and restricted to those topics which have a place in an introduction to astronomy as this discipline was understood in the Greek world. Thus, aspects of Babylonian astronomy which relate to the celestial sphere (e.g. the zodiac and the ris- ing times of the ecliptic), the luni-solar calendar (e.g. intercalation and the 19-year (“Metonic”) cycle), and lunar motion, are included, but Geminos tells us nothing about Babylonian planetary theory (the planets are only touched upon briefly by Geminos), predictive astronomy that uses planetary and lunar periods, observational astronomy, or the problem of lunar visibility, which formed major parts of Babylonian astronomical practice. -

Solar and Lunar Eclipses Reading
Eclipses What would you think if you were walking home from school on a sunny afternoon and the sun began to disappear? Would you be frightened? On rare occasions, the moon completely blocks the sun. The sky grows as dark as night even in the middle of a clear day. The air gets cool and the sky becomes an eerie color. If you don’t know what is happening, you can become very frightened. The moon doesn’t usually go directly between Earth and the sun or directly behind Earth. As the diagram below shows, the moon’s orbit around Earth is slightly tilted with respect to Earth’s orbit around the sun. As a result, in most months the moon revolves completely around Earth without the moon moving into Earth’s shadow or the moon’s shadow hitting Earth. When the moon’s shadow hits Earth or Earth’s shadow hits the moon, an eclipse occurs. An eclipse (ih klips) occurs when an object in space comes between the sun and a third object, and casts a shadow on that object. There are two types of eclipses: solar eclipses and lunar eclipses. (The words solar and lunar come from the Latin words for “sun” and “moon.”) The Tilt of the Moon’s Orbit The moon’s orbit is tilted with respect to Earth’s orbit. So the moon rarely goes directly between Earth and the sun. Solar Eclipses During a new moon, the moon is almost exactly between Earth and the sun. But most months, as you have seen, the moon travels a little above or below the sun in the sky. -

Presentation a Representation B FRONT DIALS
AGAMEMNON TSELIKAS The Anticythera Mechanism. Research Facilities and Heritage Dynamics between Humanities and Technologies NANYANG TECHNOLOGICAL UNIVERSITY EXPLORING MARITIME HERITAGE DYNAMICS 18 – 20 November 2015 Greece, Southern Aegean Sea HISTORICAL DATA * Probably was constructed in Rhodes island in the astronomical school of Poseidonius mid-2nd BC century. * It was one item of a cargo of many valuable artistic objects (bronze and marble statues) on a ship which probably departed from Rhodes in direction to Italy between the years 80 and 60 BC and wrecked south of Antikythera island. The route of the ancient ship from Rhodes to Italy. HISTORICAL DATA * It was found in 1900 a few days before Easter, by sponge divers originated from the greek island Symi in Dodekanessos near Rhodes island. The route of the sponge ship from Symi island in direction probably to Lybia. Sponge divers in their island Symi. The island of Antikythera The islands of Rhodes and Symi Sponge divers, officials, and crew of the war ship "Mykali" during the hauling of antiquities from the wreck in Antikythera. Winter 1900-1901. It consists of 82 fragments. HISTORICAL DATA * Scientists who studied the the unknown object: 1902-1910 Staes, Svoronos, Rados, Albert Rem. 1930-1940 Admiral John Theofanides, Tsiner, Gynder, Chartner. 1950-1970 Derek de Solla Price (1922-1983, “Gears from the Greeks”) and Karakalos 1980-1990 Bromley and Michael Wright 1990 - Today Michael Wright and team of the Study of mechanism. Albert Rem Admiral John Theofanides The grandson of admiral Theophanidis holding the first effort of the reconstruction of the mechanism. Derek de Solla Price Michael Wright The new team of study the Antikythe ra mecha- nism Costas Xenakis, Pandelis Feleris, Rogger Hadland, David Beit, Gerasimos Makris, Michael Edmounds, Tony Freeth, Giannis Siradakis, Xenophon Mussas, Giannis Bitsakis, Agamemnon Tselikas, Mary Zafiropoulou, Helen Mangou, Bil Ambrisco, Tom Baltsbenter, Dan Gelmb, Rogger Hadland. -

The Moon and Eclipses
The Moon and Eclipses ASTR 101 September 14, 2018 • Phases of the moon • Lunar month • Solar eclipses • Lunar eclipses • Eclipse seasons 1 Moon in the Sky An image of the Earth and the Moon taken from 1 million miles away. Diameter of Moon is about ¼ of the Earth. www.nasa.gov/feature/goddard/from-a-million-miles-away-nasa-camera-shows-moon-crossing-face-of-earth • Moonlight is reflected sunlight from the lunar surface. Moon reflects about 12% of the sunlight falling on it (ie. Moon’s albedo is 12%). • Dark features visible on the Moon are plains of old lava flows, formed by ancient volcanic eruptions – When Galileo looked at the Moon through his telescope, he thought those were Oceans, so he named them as Marias. – There is no water (or atmosphere) on the Moon, but still they are known as Maria – Through a telescope large number of craters, mountains and other geological features visible. 2 Moon Phases Sunlight Sunlight full moon New moon Sunlight Sunlight Quarter moon Crescent moon • Depending on relative positions of the Earth, the Sun and the Moon we see different amount of the illuminated surface of Moon. 3 Moon Phases first quarter waxing waxing gibbous crescent Orbit of the Moon Sunlight full moon new moon position on the orbit View from the Earth waning waning gibbous last crescent quarter 4 Sun Earthshine Moon light reflected from the Earth Earth in lunar sky is about 50 times brighter than the moon from Earth. “old moon" in the new moon's arms • Night (shadowed) side of the Moon is not completely dark.