Lightweight Compression with Encryption Based on Asymmetric Numeral Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
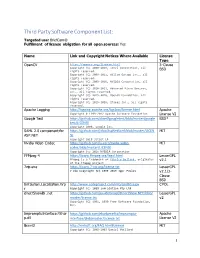
Third Party Software Component List: Targeted Use: Briefcam® Fulfillment of License Obligation for All Open Sources: Yes
Third Party Software Component List: Targeted use: BriefCam® Fulfillment of license obligation for all open sources: Yes Name Link and Copyright Notices Where Available License Type OpenCV https://opencv.org/license.html 3-Clause Copyright (C) 2000-2019, Intel Corporation, all BSD rights reserved. Copyright (C) 2009-2011, Willow Garage Inc., all rights reserved. Copyright (C) 2009-2016, NVIDIA Corporation, all rights reserved. Copyright (C) 2010-2013, Advanced Micro Devices, Inc., all rights reserved. Copyright (C) 2015-2016, OpenCV Foundation, all rights reserved. Copyright (C) 2015-2016, Itseez Inc., all rights reserved. Apache Logging http://logging.apache.org/log4cxx/license.html Apache Copyright © 1999-2012 Apache Software Foundation License V2 Google Test https://github.com/abseil/googletest/blob/master/google BSD* test/LICENSE Copyright 2008, Google Inc. SAML 2.0 component for https://github.com/jitbit/AspNetSaml/blob/master/LICEN MIT ASP.NET SE Copyright 2018 Jitbit LP Nvidia Video Codec https://github.com/lu-zero/nvidia-video- MIT codec/blob/master/LICENSE Copyright (c) 2016 NVIDIA Corporation FFMpeg 4 https://www.ffmpeg.org/legal.html LesserGPL FFmpeg is a trademark of Fabrice Bellard, originator v2.1 of the FFmpeg project 7zip.exe https://www.7-zip.org/license.txt LesserGPL 7-Zip Copyright (C) 1999-2019 Igor Pavlov v2.1/3- Clause BSD Infralution.Localization.Wp http://www.codeproject.com/info/cpol10.aspx CPOL f Copyright (C) 2018 Infralution Pty Ltd directShowlib .net https://github.com/pauldotknopf/DirectShow.NET/blob/ LesserGPL -

The Perceptual Impact of Different Quantization Schemes in G.719
The perceptual impact of different quantization schemes in G.719 BOTE LIU Master’s Degree Project Stockholm, Sweden May 2013 XR-EE-SIP 2013:001 Abstract In this thesis, three kinds of quantization schemes, Fast Lattice Vector Quantization (FLVQ), Pyramidal Vector Quantization (PVQ) and Scalar Quantization (SQ) are studied in the framework of audio codec G.719. FLVQ is composed of an RE8 -based low-rate lattice vector quantizer and a D8 -based high-rate lattice vector quantizer. PVQ uses pyramidal points in multi-dimensional space and is very suitable for the compression of Laplacian-like sources generated from transform. SQ scheme applies a combination of uniform SQ and entropy coding. Subjective tests of these three versions of audio codecs show that FLVQ and PVQ versions of audio codecs are both better than SQ version for music signals and SQ version of audio codec performs well on speech signals, especially for male speakers. I Acknowledgements I would like to express my sincere gratitude to Ericsson Research, which provides me with such a good thesis work to do. I am indebted to my supervisor, Sebastian Näslund, for sparing time to communicate with me about my work every week and giving me many valuable suggestions. I am also very grateful to Volodya Grancharov and Eric Norvell for their advice and patience as well as consistent encouragement throughout the thesis. My thanks are extended to some other Ericsson researchers for attending the subjective listening evaluation in the thesis. Finally, I want to thank my examiner, Professor Arne Leijon of Royal Institute of Technology (KTH) for reviewing my report very carefully and supporting my work very much. -

Reduced-Complexity End-To-End Variational Autoencoder for on Board Satellite Image Compression
remote sensing Article Reduced-Complexity End-to-End Variational Autoencoder for on Board Satellite Image Compression Vinicius Alves de Oliveira 1,2,* , Marie Chabert 1 , Thomas Oberlin 3 , Charly Poulliat 1, Mickael Bruno 4, Christophe Latry 4, Mikael Carlavan 5, Simon Henrot 5, Frederic Falzon 5 and Roberto Camarero 6 1 IRIT/INP-ENSEEIHT, University of Toulouse, 31071 Toulouse, France; [email protected] (M.C.); [email protected] (C.P.) 2 Telecommunications for Space and Aeronautics (TéSA) Laboratory, 31500 Toulouse, France 3 ISAE-SUPAERO, University of Toulouse, 31055 Toulouse, France; [email protected] 4 CNES, 31400 Toulouse, France; [email protected] (M.B.); [email protected] (C.L.) 5 Thales Alenia Space, 06150 Cannes, France; [email protected] (M.C.); [email protected] (S.H.); [email protected] (F.F.) 6 ESA, 2201 AZ Noordwijk, The Netherlands; [email protected] * Correspondence: [email protected] Abstract: Recently, convolutional neural networks have been successfully applied to lossy image compression. End-to-end optimized autoencoders, possibly variational, are able to dramatically outperform traditional transform coding schemes in terms of rate-distortion trade-off; however, this is at the cost of a higher computational complexity. An intensive training step on huge databases allows autoencoders to learn jointly the image representation and its probability distribution, pos- sibly using a non-parametric density model or a hyperprior auxiliary autoencoder to eliminate the need for prior knowledge. However, in the context of on board satellite compression, time and memory complexities are submitted to strong constraints. -

(12) Patent Application Publication (10) Pub. No.: US 2016/0248440 A1 Lookup | | | | | | | | | | | | |
US 201602484.40A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2016/0248440 A1 Greenfield et al. (43) Pub. Date: Aug. 25, 2016 (54) SYSTEMAND METHOD FOR COMPRESSING Publication Classification DATAUSING ASYMMETRIC NUMERAL SYSTEMIS WITH PROBABILITY (51) Int. Cl. DISTRIBUTIONS H03M 7/30 (2006.01) (52) U.S. Cl. (71) Applicants: Daniel Greenfield, Cambridge (GB); CPC ....................................... H03M 730 (2013.01) Alban Rrustemi, Cambridge (GB) (72) Inventors: Daniel Greenfield, Cambridge (GB); (57) ABSTRACT Albanan Rrustemi, Cambridge (GB(GB) A data compression method using the range variant of asym (21) Appl. No.: 15/041,228 metric numeral systems to encode a data stream, where the probability distribution table is constructed using a Markov (22) Filed: Feb. 11, 2016 model. This type of encoding results in output that has higher compression ratios when compared to other compression (30) Foreign Application Priority Data algorithms and it performs particularly well with information that represents gene sequences or information related to gene Feb. 11, 2015 (GB) ................................... 1502286.6 Sequences. 128bit o 500 580 700 7so 4096 20123115 a) 8-entry SIMD lookup Vector minpos (e.g. phminposuw) 's 20 b) 16-entry SMD —- lookup | | | | | | | | | | | | | ||l Vector sub (e.g. psubw) Wector min e.g. pminuw) Vector minpos (e.g. phmirposuw) Patent Application Publication Aug. 25, 2016 Sheet 1 of 2 US 2016/0248440 A1 128bit e (165it o 500 580 700 750 4096 2012 s115 8-entry SIMD Vector sub a) lookup (e.g. pSubw) 770 270 190 70 20 (ufi) (ufi) (uf) Vector minpos (e.g. phminposuw) b) 16-entry SIMD lookup Vector sub Vector sub (e.g. -

FFV1 Video Codec Specification
FFV1 Video Codec Specification by Michael Niedermayer [email protected] Contents 1 Introduction 2 2 Terms and Definitions 2 2.1 Terms ................................................. 2 2.2 Definitions ............................................... 2 3 Conventions 3 3.1 Arithmetic operators ......................................... 3 3.2 Assignment operators ........................................ 3 3.3 Comparison operators ........................................ 3 3.4 Order of operation precedence .................................... 4 3.5 Range ................................................. 4 3.6 Bitstream functions .......................................... 4 4 General Description 5 4.1 Border ................................................. 5 4.2 Median predictor ........................................... 5 4.3 Context ................................................ 5 4.4 Quantization ............................................. 5 4.5 Colorspace ............................................... 6 4.5.1 JPEG2000-RCT ....................................... 6 4.6 Coding of the sample difference ................................... 6 4.6.1 Range coding mode ..................................... 6 4.6.2 Huffman coding mode .................................... 9 5 Bitstream 10 5.1 Configuration Record ......................................... 10 5.1.1 In AVI File Format ...................................... 11 5.1.2 In ISO/IEC 14496-12 (MP4 File Format) ......................... 11 5.1.3 In NUT File Format .................................... -
![Asymmetric Numeral Systems. Arxiv:0902.0271V5 [Cs.IT]](https://docslib.b-cdn.net/cover/1387/asymmetric-numeral-systems-arxiv-0902-0271v5-cs-it-1161387.webp)
Asymmetric Numeral Systems. Arxiv:0902.0271V5 [Cs.IT]
Asymmetric numeral systems. Jarek Duda Jagiellonian University, Poland, email: [email protected] Abstract In this paper will be presented new approach to entropy coding: family of generalizations of standard numeral systems which are optimal for encoding sequence of equiprobable symbols, into asymmetric numeral systems - optimal for freely chosen probability distributions of symbols. It has some similarities to Range Coding but instead of encoding symbol in choosing a range, we spread these ranges uniformly over the whole interval. This leads to simpler encoder - instead of using two states to define range, we need only one. This approach is very universal - we can obtain from extremely precise encoding (ABS) to extremely fast with possibility to additionally encrypt the data (ANS). This encryption uses the key to initialize random number generator, which is used to calculate the coding tables. Such preinitialized encryption has additional advantage: is resistant to brute force attack - to check a key we have to make whole initialization. There will be also presented application for new approach to error correction: after an error in each step we have chosen probability to observe that something was wrong. We can get near Shannon's limit for any noise level this way with expected linear time of correction. arXiv:0902.0271v5 [cs.IT] 21 May 2009 1 Introduction In practice there are used two approaches for entropy coding nowadays: building binary tree (Huffman coding [1]) and arithmetic/range coding ([2],[3]). The first one approximates probabilities of symbols with powers of 2 - isn't precise. Arithmetic coding is precise. It encodes symbol in choosing one of large ranges of length proportional to assumed probability distribution (q). -

The Deep Learning Solutions on Lossless Compression Methods for Alleviating Data Load on Iot Nodes in Smart Cities
sensors Article The Deep Learning Solutions on Lossless Compression Methods for Alleviating Data Load on IoT Nodes in Smart Cities Ammar Nasif *, Zulaiha Ali Othman and Nor Samsiah Sani Center for Artificial Intelligence Technology (CAIT), Faculty of Information Science & Technology, University Kebangsaan Malaysia, Bangi 43600, Malaysia; [email protected] (Z.A.O.); [email protected] (N.S.S.) * Correspondence: [email protected] Abstract: Networking is crucial for smart city projects nowadays, as it offers an environment where people and things are connected. This paper presents a chronology of factors on the development of smart cities, including IoT technologies as network infrastructure. Increasing IoT nodes leads to increasing data flow, which is a potential source of failure for IoT networks. The biggest challenge of IoT networks is that the IoT may have insufficient memory to handle all transaction data within the IoT network. We aim in this paper to propose a potential compression method for reducing IoT network data traffic. Therefore, we investigate various lossless compression algorithms, such as entropy or dictionary-based algorithms, and general compression methods to determine which algorithm or method adheres to the IoT specifications. Furthermore, this study conducts compression experiments using entropy (Huffman, Adaptive Huffman) and Dictionary (LZ77, LZ78) as well as five different types of datasets of the IoT data traffic. Though the above algorithms can alleviate the IoT data traffic, adaptive Huffman gave the best compression algorithm. Therefore, in this paper, Citation: Nasif, A.; Othman, Z.A.; we aim to propose a conceptual compression method for IoT data traffic by improving an adaptive Sani, N.S. -

Key-Based Self-Driven Compression in Columnar Binary JSON
Otto von Guericke University of Magdeburg Department of Computer Science Master's Thesis Key-Based Self-Driven Compression in Columnar Binary JSON Author: Oskar Kirmis November 4, 2019 Advisors: Prof. Dr. rer. nat. habil. Gunter Saake M. Sc. Marcus Pinnecke Institute for Technical and Business Information Systems / Database Research Group Kirmis, Oskar: Key-Based Self-Driven Compression in Columnar Binary JSON Master's Thesis, Otto von Guericke University of Magdeburg, 2019 Abstract A large part of the data that is available today in organizations or publicly is provided in semi-structured form. To perform analytical tasks on these { mostly read-only { semi-structured datasets, Carbon archives were developed as a column-oriented storage format. Its main focus is to allow cache-efficient access to fields across records. As many semi-structured datasets mainly consist of string data and the denormalization introduces redundancy, a lot of storage space is required. However, in Carbon archives { besides a deduplication of strings { there is currently no compression implemented. The goal of this thesis is to discuss, implement and evaluate suitable compression tech- niques to reduce the amount of storage required and to speed up analytical queries on Carbon archives. Therefore, a compressor is implemented that can be configured to apply a combination of up to three different compression algorithms to the string data of Carbon archives. This compressor can be applied with a different configuration per column (per JSON object key). To find suitable combinations of compression algo- rithms for each column, one manual and two self-driven approaches are implemented and evaluated. On a set of ten publicly available semi-structured datasets of different kinds and sizes, the string data can be compressed down to about 53% on average, reducing the whole datasets' size by 20%. -

Forcepoint DLP Supported File Formats and Size Limits
Forcepoint DLP Supported File Formats and Size Limits Supported File Formats and Size Limits | Forcepoint DLP | v8.8.1 This article provides a list of the file formats that can be analyzed by Forcepoint DLP, file formats from which content and meta data can be extracted, and the file size limits for network, endpoint, and discovery functions. See: ● Supported File Formats ● File Size Limits © 2021 Forcepoint LLC Supported File Formats Supported File Formats and Size Limits | Forcepoint DLP | v8.8.1 The following tables lists the file formats supported by Forcepoint DLP. File formats are in alphabetical order by format group. ● Archive For mats, page 3 ● Backup Formats, page 7 ● Business Intelligence (BI) and Analysis Formats, page 8 ● Computer-Aided Design Formats, page 9 ● Cryptography Formats, page 12 ● Database Formats, page 14 ● Desktop publishing formats, page 16 ● eBook/Audio book formats, page 17 ● Executable formats, page 18 ● Font formats, page 20 ● Graphics formats - general, page 21 ● Graphics formats - vector graphics, page 26 ● Library formats, page 29 ● Log formats, page 30 ● Mail formats, page 31 ● Multimedia formats, page 32 ● Object formats, page 37 ● Presentation formats, page 38 ● Project management formats, page 40 ● Spreadsheet formats, page 41 ● Text and markup formats, page 43 ● Word processing formats, page 45 ● Miscellaneous formats, page 53 Supported file formats are added and updated frequently. Key to support tables Symbol Description Y The format is supported N The format is not supported P Partial metadata -

Answers to Exercises
Answers to Exercises A bird does not sing because he has an answer, he sings because he has a song. —Chinese Proverb Intro.1: abstemious, abstentious, adventitious, annelidous, arsenious, arterious, face- tious, sacrilegious. Intro.2: When a software house has a popular product they tend to come up with new versions. A user can update an old version to a new one, and the update usually comes as a compressed file on a floppy disk. Over time the updates get bigger and, at a certain point, an update may not fit on a single floppy. This is why good compression is important in the case of software updates. The time it takes to compress and decompress the update is unimportant since these operations are typically done just once. Recently, software makers have taken to providing updates over the Internet, but even in such cases it is important to have small files because of the download times involved. 1.1: (1) ask a question, (2) absolutely necessary, (3) advance warning, (4) boiling hot, (5) climb up, (6) close scrutiny, (7) exactly the same, (8) free gift, (9) hot water heater, (10) my personal opinion, (11) newborn baby, (12) postponed until later, (13) unexpected surprise, (14) unsolved mysteries. 1.2: A reasonable way to use them is to code the five most-common strings in the text. Because irreversible text compression is a special-purpose method, the user may know what strings are common in any particular text to be compressed. The user may specify five such strings to the encoder, and they should also be written at the start of the output stream, for the decoder’s use. -

In-Core Compression: How to Shrink Your Database Size in Several Times
In-core compression: how to shrink your database size in several times Aleksander Alekseev Anastasia Lubennikova www.postgrespro.ru Agenda ● What does Postgres store? • A couple of words about storage internals ● Check list for your schema • A set of tricks to optimize database size ● In-core block level compression • Out-of-box feature of Postgres Pro EE ● ZSON • Extension for transparent JSONB compression What this talk doesn’t cover ● MVCC bloat • Tune autovacuum properly • Drop unused indexes • Use pg_repack • Try pg_squeeze ● Catalog bloat • Create less temporary tables ● WAL-log size • Enable wal_compression ● FS level compression • ZFS, btrfs, etc Data layout Empty tables are not that empty ● Imagine we have no data create table tbl(); insert into tbl select from generate_series(0,1e07); select pg_size_pretty(pg_relation_size('tbl')); pg_size_pretty --------------- ??? Empty tables are not that empty ● Imagine we have no data create table tbl(); insert into tbl select from generate_series(0,1e07); select pg_size_pretty(pg_relation_size('tbl')); pg_size_pretty --------------- 268 MB Meta information db=# select * from heap_page_items(get_raw_page('tbl',0)); -[ RECORD 1 ]------------------- lp | 1 lp_off | 8160 lp_flags | 1 lp_len | 32 t_xmin | 720 t_xmax | 0 t_field3 | 0 t_ctid | (0,1) t_infomask2 | 2 t_infomask | 2048 t_hoff | 24 t_bits | t_oid | t_data | Order matters ● Attributes must be aligned inside the row create table bad (i1 int, b1 bigint, i1 int); create table good (i1 int, i1 int, b1 bigint); Safe up to 20% of space. -
![Asymmetric Numeral Systems As Close to Capacity Low State Entropy Coders Arxiv:1311.2540V1 [Cs.IT] 11 Nov 2013](https://docslib.b-cdn.net/cover/4000/asymmetric-numeral-systems-as-close-to-capacity-low-state-entropy-coders-arxiv-1311-2540v1-cs-it-11-nov-2013-2244000.webp)
Asymmetric Numeral Systems As Close to Capacity Low State Entropy Coders Arxiv:1311.2540V1 [Cs.IT] 11 Nov 2013
Asymmetric numeral systems as close to capacity low state entropy coders Jarek Duda Center for Science of Information, Purdue University, W. Lafayette, IN 47907, U.S.A. email: [email protected] Abstract Imagine a basic situation: we have a source of symbols of known probability distribution and we would like to design an entropy coder transforming it into a bit sequence, which would be simple and very close to the capacity (Shannon entropy). Prefix codes are the basic method, defining "symbol!bit sequence" set of rules, usually found using Huffman algorithm. They theoretically allow to reduce the dis- tance from the capacity (∆H) down to zero, but the cost grows rapidly. We will discuss improving it by replacing this memoryless coder with an automate having some small set of internal states: defined by "(symbol, state)!(bit sequence, new state)" set of rules. The natural question is the minimal number of states to achieve given performance, what is especially important for simple high throughput hard- ware coders. Arithmetic coding can be seen this way, but it requires relatively large number of states (possible ranges). We will discuss asymmetric numeral systems (ANS) for this purpose, which can be seen as asymmetrization of numeral systems. Less than 20 states will be usually sufficient to achieve ∆H ≈ 0:001 bits/symbol for a small alphabet. ∆H generally generally decreases approximately like 1/(the number of states)2 and increases proportionally the size of alphabet. Huge freedom of choosing the exact coding and chaotic behavior of state make it also perfect to simultaneously encrypt the data.