Euler Angles and 3D Rotations by Matrix Methods
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Understanding Euler Angles 1
Welcome Guest View Cart (0 items) Login Home Products Support News About Us Understanding Euler Angles 1. Introduction Attitude and Heading Sensors from CH Robotics can provide orientation information using both Euler Angles and Quaternions. Compared to quaternions, Euler Angles are simple and intuitive and they lend themselves well to simple analysis and control. On the other hand, Euler Angles are limited by a phenomenon called "Gimbal Lock," which we will investigate in more detail later. In applications where the sensor will never operate near pitch angles of +/‐ 90 degrees, Euler Angles are a good choice. Sensors from CH Robotics that can provide Euler Angle outputs include the GP9 GPS‐Aided AHRS, and the UM7 Orientation Sensor. Figure 1 ‐ The Inertial Frame Euler angles provide a way to represent the 3D orientation of an object using a combination of three rotations about different axes. For convenience, we use multiple coordinate frames to describe the orientation of the sensor, including the "inertial frame," the "vehicle‐1 frame," the "vehicle‐2 frame," and the "body frame." The inertial frame axes are Earth‐fixed, and the body frame axes are aligned with the sensor. The vehicle‐1 and vehicle‐2 are intermediary frames used for convenience when illustrating the sequence of operations that take us from the inertial frame to the body frame of the sensor. It may seem unnecessarily complicated to use four different coordinate frames to describe the orientation of the sensor, but the motivation for doing so will become clear as we proceed. For clarity, this application note assumes that the sensor is mounted to an aircraft. -

The Rolling Ball Problem on the Sphere
S˜ao Paulo Journal of Mathematical Sciences 6, 2 (2012), 145–154 The rolling ball problem on the sphere Laura M. O. Biscolla Universidade Paulista Rua Dr. Bacelar, 1212, CEP 04026–002 S˜aoPaulo, Brasil Universidade S˜aoJudas Tadeu Rua Taquari, 546, CEP 03166–000, S˜aoPaulo, Brasil E-mail address: [email protected] Jaume Llibre Departament de Matem`atiques, Universitat Aut`onomade Barcelona 08193 Bellaterra, Barcelona, Catalonia, Spain E-mail address: [email protected] Waldyr M. Oliva CAMGSD, LARSYS, Instituto Superior T´ecnico, UTL Av. Rovisco Pais, 1049–0011, Lisbon, Portugal Departamento de Matem´atica Aplicada Instituto de Matem´atica e Estat´ıstica, USP Rua do Mat˜ao,1010–CEP 05508–900, S˜aoPaulo, Brasil E-mail address: [email protected] Dedicated to Lu´ıs Magalh˜aes and Carlos Rocha on the occasion of their 60th birthdays Abstract. By a sequence of rolling motions without slipping or twist- ing along arcs of great circles outside the surface of a sphere of radius R, a spherical ball of unit radius has to be transferred from an initial state to an arbitrary final state taking into account the orientation of the ball. Assuming R > 1 we provide a new and shorter prove of the result of Frenkel and Garcia in [4] that with at most 4 moves we can go from a given initial state to an arbitrary final state. Important cases such as the so called elimination of the spin discrepancy are done with 3 moves only. 1991 Mathematics Subject Classification. Primary 58E25, 93B27. Key words: Control theory, rolling ball problem. -

Chapter 5 ANGULAR MOMENTUM and ROTATIONS
Chapter 5 ANGULAR MOMENTUM AND ROTATIONS In classical mechanics the total angular momentum L~ of an isolated system about any …xed point is conserved. The existence of a conserved vector L~ associated with such a system is itself a consequence of the fact that the associated Hamiltonian (or Lagrangian) is invariant under rotations, i.e., if the coordinates and momenta of the entire system are rotated “rigidly” about some point, the energy of the system is unchanged and, more importantly, is the same function of the dynamical variables as it was before the rotation. Such a circumstance would not apply, e.g., to a system lying in an externally imposed gravitational …eld pointing in some speci…c direction. Thus, the invariance of an isolated system under rotations ultimately arises from the fact that, in the absence of external …elds of this sort, space is isotropic; it behaves the same way in all directions. Not surprisingly, therefore, in quantum mechanics the individual Cartesian com- ponents Li of the total angular momentum operator L~ of an isolated system are also constants of the motion. The di¤erent components of L~ are not, however, compatible quantum observables. Indeed, as we will see the operators representing the components of angular momentum along di¤erent directions do not generally commute with one an- other. Thus, the vector operator L~ is not, strictly speaking, an observable, since it does not have a complete basis of eigenstates (which would have to be simultaneous eigenstates of all of its non-commuting components). This lack of commutivity often seems, at …rst encounter, as somewhat of a nuisance but, in fact, it intimately re‡ects the underlying structure of the three dimensional space in which we are immersed, and has its source in the fact that rotations in three dimensions about di¤erent axes do not commute with one another. -
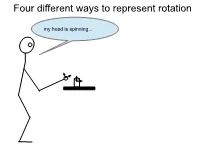
Euler Quaternions
Four different ways to represent rotation my head is spinning... The space of rotations SO( 3) = {R ∈ R3×3 | RRT = I,det(R) = +1} Special orthogonal group(3): Why det( R ) = ± 1 ? − = − Rotations preserve distance: Rp1 Rp2 p1 p2 Rotations preserve orientation: ( ) × ( ) = ( × ) Rp1 Rp2 R p1 p2 The space of rotations SO( 3) = {R ∈ R3×3 | RRT = I,det(R) = +1} Special orthogonal group(3): Why it’s a group: • Closed under multiplication: if ∈ ( ) then ∈ ( ) R1, R2 SO 3 R1R2 SO 3 • Has an identity: ∃ ∈ ( ) = I SO 3 s.t. IR1 R1 • Has a unique inverse… • Is associative… Why orthogonal: • vectors in matrix are orthogonal Why it’s special: det( R ) = + 1 , NOT det(R) = ±1 Right hand coordinate system Possible rotation representations You need at least three numbers to represent an arbitrary rotation in SO(3) (Euler theorem). Some three-number representations: • ZYZ Euler angles • ZYX Euler angles (roll, pitch, yaw) • Axis angle One four-number representation: • quaternions ZYZ Euler Angles φ = θ rzyz ψ φ − φ cos sin 0 To get from A to B: φ = φ φ Rz ( ) sin cos 0 1. Rotate φ about z axis 0 0 1 θ θ 2. Then rotate θ about y axis cos 0 sin θ = ψ Ry ( ) 0 1 0 3. Then rotate about z axis − sinθ 0 cosθ ψ − ψ cos sin 0 ψ = ψ ψ Rz ( ) sin cos 0 0 0 1 ZYZ Euler Angles φ θ ψ Remember that R z ( ) R y ( ) R z ( ) encode the desired rotation in the pre- rotation reference frame: φ = pre−rotation Rz ( ) Rpost−rotation Therefore, the sequence of rotations is concatentated as follows: (φ θ ψ ) = φ θ ψ Rzyz , , Rz ( )Ry ( )Rz ( ) φ − φ θ θ ψ − ψ cos sin 0 cos 0 sin cos sin 0 (φ θ ψ ) = φ φ ψ ψ Rzyz , , sin cos 0 0 1 0 sin cos 0 0 0 1− sinθ 0 cosθ 0 0 1 − − − cφ cθ cψ sφ sψ cφ cθ sψ sφ cψ cφ sθ (φ θ ψ ) = + − + Rzyz , , sφ cθ cψ cφ sψ sφ cθ sψ cφ cψ sφ sθ − sθ cψ sθ sψ cθ ZYX Euler Angles (roll, pitch, yaw) φ − φ cos sin 0 To get from A to B: φ = φ φ Rz ( ) sin cos 0 1. -

Theory of Angular Momentum and Spin
Chapter 5 Theory of Angular Momentum and Spin Rotational symmetry transformations, the group SO(3) of the associated rotation matrices and the 1 corresponding transformation matrices of spin{ 2 states forming the group SU(2) occupy a very important position in physics. The reason is that these transformations and groups are closely tied to the properties of elementary particles, the building blocks of matter, but also to the properties of composite systems. Examples of the latter with particularly simple transformation properties are closed shell atoms, e.g., helium, neon, argon, the magic number nuclei like carbon, or the proton and the neutron made up of three quarks, all composite systems which appear spherical as far as their charge distribution is concerned. In this section we want to investigate how elementary and composite systems are described. To develop a systematic description of rotational properties of composite quantum systems the consideration of rotational transformations is the best starting point. As an illustration we will consider first rotational transformations acting on vectors ~r in 3-dimensional space, i.e., ~r R3, 2 we will then consider transformations of wavefunctions (~r) of single particles in R3, and finally N transformations of products of wavefunctions like j(~rj) which represent a system of N (spin- Qj=1 zero) particles in R3. We will also review below the well-known fact that spin states under rotations behave essentially identical to angular momentum states, i.e., we will find that the algebraic properties of operators governing spatial and spin rotation are identical and that the results derived for products of angular momentum states can be applied to products of spin states or a combination of angular momentum and spin states. -

Rotation Matrix - Wikipedia, the Free Encyclopedia Page 1 of 22
Rotation matrix - Wikipedia, the free encyclopedia Page 1 of 22 Rotation matrix From Wikipedia, the free encyclopedia In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example the matrix rotates points in the xy -Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv (see below for details). In two and three dimensions, rotation matrices are among the simplest algebraic descriptions of rotations, and are used extensively for computations in geometry, physics, and computer graphics. Though most applications involve rotations in two or three dimensions, rotation matrices can be defined for n-dimensional space. Rotation matrices are always square, with real entries. Algebraically, a rotation matrix in n-dimensions is a n × n special orthogonal matrix, i.e. an orthogonal matrix whose determinant is 1: . The set of all rotation matrices forms a group, known as the rotation group or the special orthogonal group. It is a subset of the orthogonal group, which includes reflections and consists of all orthogonal matrices with determinant 1 or -1, and of the special linear group, which includes all volume-preserving transformations and consists of matrices with determinant 1. Contents 1 Rotations in two dimensions 1.1 Non-standard orientation -

A Tutorial on Euler Angles and Quaternions
A Tutorial on Euler Angles and Quaternions Moti Ben-Ari Department of Science Teaching Weizmann Institute of Science http://www.weizmann.ac.il/sci-tea/benari/ Version 2.0.1 c 2014–17 by Moti Ben-Ari. This work is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/ by-sa/3.0/ or send a letter to Creative Commons, 444 Castro Street, Suite 900, Mountain View, California, 94041, USA. Chapter 1 Introduction You sitting in an airplane at night, watching a movie displayed on the screen attached to the seat in front of you. The airplane gently banks to the left. You may feel the slight acceleration, but you won’t see any change in the position of the movie screen. Both you and the screen are in the same frame of reference, so unless you stand up or make another move, the position and orientation of the screen relative to your position and orientation won’t change. The same is not true with respect to your position and orientation relative to the frame of reference of the earth. The airplane is moving forward at a very high speed and the bank changes your orientation with respect to the earth. The transformation of coordinates (position and orientation) from one frame of reference is a fundamental operation in several areas: flight control of aircraft and rockets, move- ment of manipulators in robotics, and computer graphics. This tutorial introduces the mathematics of rotations using two formalisms: (1) Euler angles are the angles of rotation of a three-dimensional coordinate frame. -

Chapter 1 Rigid Body Kinematics
Chapter 1 Rigid Body Kinematics 1.1 Introduction This chapter builds up the basic language and tools to describe the motion of a rigid body – this is called rigid body kinematics. This material will be the foundation for describing general mech- anisms consisting of interconnected rigid bodies in various topologies that are the focus of this book. Only the geometric property of the body and its evolution in time will be studied; the re- sponse of the body to externally applied forces is covered in Chapter ?? under the topic of rigid body dynamics. Rigid body kinematics is not only useful in the analysis of robotic mechanisms, but also has many other applications, such as in the analysis of planetary motion, ground, air, and water vehicles, limbs and bodies of humans and animals, and computer graphics and virtual reality. Indeed, in 1765, motivated by the precession of the equinoxes, Leonhard Euler decomposed a rigid body motion to a translation and rotation, parameterized rotation by three principal-axis rotation (Euler angles), and proved the famous Euler’s rotation theorem [?]. A body is rigid if the distance between any two points fixed with respect to the body remains constant. If the body is free to move and rotate in space, it has 6 degree-of-freedom (DOF), 3 trans- lational and 3 rotational, if we consider both translation and rotation. If the body is constrained in a plane, then it is 3-DOF, 2 translational and 1 rotational. We will adopt a coordinate-free ap- proach as in [?, ?] and use geometric, rather than purely algebraic, arguments as much as possible. -

3D Rigid Body Dynamics: Tops and Gyroscopes
J. Peraire, S. Widnall 16.07 Dynamics Fall 2008 Version 2.0 Lecture L30 - 3D Rigid Body Dynamics: Tops and Gyroscopes 3D Rigid Body Dynamics: Euler Equations in Euler Angles In lecture 29, we introduced the Euler angles as a framework for formulating and solving the equations for conservation of angular momentum. We applied this framework to the free-body motion of a symmetrical body whose angular momentum vector was not aligned with a principal axis. The angular moment was however constant. We now apply Euler angles and Euler’s equations to a slightly more general case, a top or gyroscope in the presence of gravity. We consider a top rotating about a fixed point O on a flat plane in the presence of gravity. Unlike our previous example of free-body motion, the angular momentum vector is not aligned with the Z axis, but precesses about the Z axis due to the applied moment. Whether we take the origin at the center of mass G or the fixed point O, the applied moment about the x axis is Mx = MgzGsinθ, where zG is the distance to the center of mass.. Initially, we shall not assume steady motion, but will develop Euler’s equations in the Euler angle variables ψ (spin), φ (precession) and θ (nutation). 1 Referring to the figure showing the Euler angles, and referring to our study of free-body motion, we have the following relationships between the angular velocities along the x, y, z axes and the time rate of change of the Euler angles. The angular velocity vectors for θ˙, φ˙ and ψ˙ are shown in the figure. -

Rotations and Angular Momentum
rotations.nb:11/3/04::13:48:13 1 RotationsandAngularmomentum Á Intro Thematerialheremaybefoundin SakuraiChap3:1-3,(5-6),7,(9-10) MerzbacherChap11,17. Chapter11ofMerzbacherconcentratesonorbitalangularmomentum.Sakurai,andCh17ofMerzbacherfocuson angularmomentuminrelationtothegroupofrotations.Justaslinearmomentumisrelatedtothetranslationgroup, angularmomentumoperatorsaregeneratorsofrotations.Thegoalistopresentthebasicsin5lecturesfocusingon 1.J asthegeneratorofrotations. 2.RepresentationsofSO 3 3.Additionofangularmomentum+ / 4.OrbitalangularmomentumandYlm ' s 5.Tensoroperators. Á Rotations&SO(3) ü Rotationsofvectors Beginwithadiscussionofrotationsappliedtoa3-dimensionalrealvectorspace.Thevectorsaredescribedbythreereal vx numbers,e.g.v = v .ThetransposeofavectorisvT = v , v , v .Thereisaninnerproductdefinedbetweentwo ML y ]\ x y z M ] M vz ] + / T M T ] vectorsbyu ÿ v =Nv ÿ^u = uv cos f,wherefistheanglebetweenthetwovectors.Underarotationtheinnerproduct betweenanytwovectorsispreserved,i.e.thelengthofanyvectorandtheanglebetweenanytwovectorsdoesn't change.Arotationcanbedescribedbya3ä3realorthogonalmatrixRwhichoperatesonavectorbytheusualrulesof matrixmultiplication v'x vx v' = R v and v' , v' , v' = v , v , v RT ML y ]\ ML y ]\ x y z x y z M ] M ] M v'z ] M vz ] + / + / M ]]] M ]]] N ^ N ^ Topreservetheinnerproduct,itisrequirdthatRT ÿ R = 1 u'ÿ v' = uRT ÿ Rv = u1v = u ÿ v Asanexample,arotationbyfaroundthez-axis(orinthexy-plane)isgivenby rotations.nb:11/3/04::13:48:13 2 cos f -sin f 0 R f = sin f cos f 0 z ML ]\ M ] + / M 0 0 1 ] M ]]] N ^ Thesignconventionsareappropriateforarighthandedcoordinatesystem:putthethumbofrighthandalongz-axis, -

CS 4733 Class Notes: Composite Rotations 1 Euler Angles
CS 4733 Class Notes: Composite Rotations 1 Euler Angles We can represent rotation in space by rotating about the 3 coordinate axes, X; Y; Z. The particular order we do this is somewhat arbitrary. If we choose 1 of the 3 axes as the first rotation, then there are 2 choices for the second rotation axis (we can’t use the same axis twice in a row), and 2 choices for the third axis. This leaves 3 × 2 × 2 = 12 choices for possible sequences of 3 rotations. The angles for each of the 3 rotations are referred to as Euler angles. A very popular and widely used set of Euler angles is ZYZ: a rotation about the world Z frame, followed by a rotation about Y in the new local frame, followed by another rotation about Z in the local frame. CφCθC − SφS −CφCθS − SφC CφSθ 0 SφCθC + CφS −SφCθS + CφC SφSθ 0 Rot(Z; φ) Rot(Y; θ) Rot(Z; ) = 2 3 (1) −SθC SθS Cθ 0 6 7 6 0 0 0 1 7 6 7 4 5 We can derive this equation by simpling multiplying the three elementary rotation matrices together. Once we know the form of this transform matrix, we can use it to find the Euler angles given the transfor- mation matrix. Said another way, if we have a final position and orientation matrix, we can break out of this matrix the Euler anlges that can get us there. So given an arbitrary transform: nx ox ax px n o a p 2 y y y y 3 (2) nz oz az pz 6 7 6 0 0 0 1 7 6 7 4 5 φ = AT AN2(ay ; ax) or φ = AT AN2(−ay ; −ax) = AT AN2(−nxSφ + nyCφ ; −oxSφ + oyCφ) θ = AT AN2(axCφ + aySφ ; az) 1 2 Roll, Pitch, Yaw Angles Figure 1: Roll, Pitch and Yaw angles A common representation for orientation is to use roll, pitch and yaw angles. -

Relationship Between Euler-Angle Rates and Body-Axis Rates
Relationship Between Euler-Angle Rates and Body-Axis Rates ! $ ! $ ! $ •! " ˙ is measured in the Inertial Frame p '! 0 ! $ # & # & # & # 0 & "˙ B ! B 2 •! is measured in Intermediate Frame #1 # q & = I3 # 0 &+ H2 # ( &+ H2 H1 # 0 & •! " ˙ is measured in Intermediate Frame #2 # & "# 0 %& "# 0 %& # )! & " r % " % •! ... which is ! $ ! ' ( $! )! $ # p & # 1 0 sin &# & Can the inversion ) ) ( B ! # q & = # 0 cos sin cos &# (! & = LI + become singular? # & # &# & " r % " 0 'sin) cos) cos( % *! What does this mean? " % Inverse transformation [(.)-1 ! (.)T] $ ' !! $ ! " ! " '$ ' & ) & 1 sin tan cos tan )& p ) & ! ) I " = & 0 cos! *sin! )& q ) = LB+B & #! ) & )& ) % ( % 0 sin! sec" cos! sec" (% r ( 1 Euler-Angle Rates and Body-Axis Rates 2 Avoiding the Euler Angle Singularity at ! = ±90° !! Alternatives to Euler angles -! Direction cosine (rotation) matrix -! Quaternions Propagation of direction cosine matrix (9 parameters) ! I = !" I HBhB I HBhB Consequently # 0 !r() t q() t & % ( ! B B B HI ()t = !"" B ()t HI ()t = ! % r() t 0 ! p() t ( HI ()t % ( % !q() t p() t 0()t ( $ 'B HB ()0 = HB ! ," ,# I I ()0 0 0 3 Avoiding the Euler Angle Singularity at ! = ±90° Propagation of quaternion vector: single rotation from inertial to body frame (4 parameters) !! Rotation from one axis system, I, to another, B, represented by !! Orientation of axis vector about which the rotation occurs (3 parameters of a unit vector, a1, a2, and a3) !! Magnitude of the rotation angle, ", rad 4 Euler Rotation of a Vector Rotation of a vector to an arbitrary new orientation