Section 1.1 Calculus: Areas and Tangents 3
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Infinitesimal and Tangent to Polylogarithmic Complexes For
AIMS Mathematics, 4(4): 1248–1257. DOI:10.3934/math.2019.4.1248 Received: 11 June 2019 Accepted: 11 August 2019 http://www.aimspress.com/journal/Math Published: 02 September 2019 Research article Infinitesimal and tangent to polylogarithmic complexes for higher weight Raziuddin Siddiqui* Department of Mathematical Sciences, Institute of Business Administration, Karachi, Pakistan * Correspondence: Email: [email protected]; Tel: +92-213-810-4700 Abstract: Motivic and polylogarithmic complexes have deep connections with K-theory. This article gives morphisms (different from Goncharov’s generalized maps) between |-vector spaces of Cathelineau’s infinitesimal complex for weight n. Our morphisms guarantee that the sequence of infinitesimal polylogs is a complex. We are also introducing a variant of Cathelineau’s complex with the derivation map for higher weight n and suggesting the definition of tangent group TBn(|). These tangent groups develop the tangent to Goncharov’s complex for weight n. Keywords: polylogarithm; infinitesimal complex; five term relation; tangent complex Mathematics Subject Classification: 11G55, 19D, 18G 1. Introduction The classical polylogarithms represented by Lin are one valued functions on a complex plane (see [11]). They are called generalization of natural logarithms, which can be represented by an infinite series (power series): X1 zk Li (z) = = − ln(1 − z) 1 k k=1 X1 zk Li (z) = 2 k2 k=1 : : X1 zk Li (z) = for z 2 ¼; jzj < 1 n kn k=1 The other versions of polylogarithms are Infinitesimal (see [8]) and Tangential (see [9]). We will discuss group theoretic form of infinitesimal and tangential polylogarithms in x 2.3, 2.4 and 2.5 below. -

2. the Tangent Line
2. The Tangent Line The tangent line to a circle at a point P on its circumference is the line perpendicular to the radius of the circle at P. In Figure 1, The line T is the tangent line which is Tangent Line perpendicular to the radius of the circle at the point P. T Figure 1: A Tangent Line to a Circle While the tangent line to a circle has the property that it is perpendicular to the radius at the point of tangency, it is not this property which generalizes to other curves. We shall make an observation about the tangent line to the circle which is carried over to other curves, and may be used as its defining property. Let us look at a specific example. Let the equation of the circle in Figure 1 be x22 + y = 25. We may easily determine the equation of the tangent line to this circle at the point P(3,4). First, we observe that the radius is a segment of the line passing through the origin (0, 0) and P(3,4), and its equation is (why?). Since the tangent line is perpendicular to this line, its slope is -3/4 and passes through P(3, 4), using the point-slope formula, its equation is found to be Let us compute y-values on both the tangent line and the circle for x-values near the point P(3, 4). Note that near P, we can solve for the y-value on the upper half of the circle which is found to be When x = 3.01, we find the y-value on the tangent line is y = -3/4(3.01) + 25/4 = 3.9925, while the corresponding value on the circle is (Note that the tangent line lie above the circle, so its y-value was expected to be a larger.) In Table 1, we indicate other corresponding values as we vary x near P. -
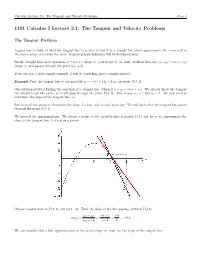
1101 Calculus I Lecture 2.1: the Tangent and Velocity Problems
Calculus Lecture 2.1: The Tangent and Velocity Problems Page 1 1101 Calculus I Lecture 2.1: The Tangent and Velocity Problems The Tangent Problem A good way to think of what the tangent line to a curve is that it is a straight line which approximates the curve well in the region where it touches the curve. A more precise definition will be developed later. Recall, straight lines have equations y = mx + b (slope m, y-intercept b), or, more useful in this case, y − y0 = m(x − x0) (slope m, and passes through the point (x0, y0)). Your text has a fairly simple example. I will do something more complex instead. Example Find the tangent line to the parabola y = −3x2 + 12x − 8 at the point P (3, 1). Our solution involves finding the equation of a straight line, which is y − y0 = m(x − x0). We already know the tangent line should touch the curve, so it will pass through the point P (3, 1). This means x0 = 3 and y0 = 1. We now need to determine the slope of the tangent line, m. But we need two points to determine the slope of a line, and we only know one. We only know that the tangent line passes through the point P (3, 1). We proceed by approximations. We choose a point on the parabola that is nearby (3,1) and use it to approximate the slope of the tangent line. Let’s draw a sketch. Choose a point close to P (3, 1), say Q(4, −8). -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Calculus Formulas and Theorems
Formulas and Theorems for Reference I. Tbigonometric Formulas l. sin2d+c,cis2d:1 sec2d l*cot20:<:sc:20 +.I sin(-d) : -sitt0 t,rs(-//) = t r1sl/ : -tallH 7. sin(A* B) :sitrAcosB*silBcosA 8. : siri A cos B - siu B <:os,;l 9. cos(A+ B) - cos,4cos B - siuA siriB 10. cos(A- B) : cosA cosB + silrA sirrB 11. 2 sirrd t:osd 12. <'os20- coS2(i - siu20 : 2<'os2o - I - 1 - 2sin20 I 13. tan d : <.rft0 (:ost/ I 14. <:ol0 : sirrd tattH 1 15. (:OS I/ 1 16. cscd - ri" 6i /F tl r(. cos[I ^ -el : sitt d \l 18. -01 : COSA 215 216 Formulas and Theorems II. Differentiation Formulas !(r") - trr:"-1 Q,:I' ]tra-fg'+gf' gJ'-,f g' - * (i) ,l' ,I - (tt(.r))9'(.,') ,i;.[tyt.rt) l'' d, \ (sttt rrJ .* ('oqI' .7, tJ, \ . ./ stll lr dr. l('os J { 1a,,,t,:r) - .,' o.t "11'2 1(<,ot.r') - (,.(,2.r' Q:T rl , (sc'c:.r'J: sPl'.r tall 11 ,7, d, - (<:s<t.r,; - (ls(].]'(rot;.r fr("'),t -.'' ,1 - fr(u") o,'ltrc ,l ,, 1 ' tlll ri - (l.t' .f d,^ --: I -iAl'CSllLl'l t!.r' J1 - rz 1(Arcsi' r) : oT Il12 Formulas and Theorems 2I7 III. Integration Formulas 1. ,f "or:artC 2. [\0,-trrlrl *(' .t "r 3. [,' ,t.,: r^x| (' ,I 4. In' a,,: lL , ,' .l 111Q 5. In., a.r: .rhr.r' .r r (' ,l f 6. sirr.r d.r' - ( os.r'-t C ./ 7. /.,,.r' dr : sitr.i'| (' .t 8. tl:r:hr sec,rl+ C or ln Jccrsrl+ C ,f'r^rr f 9. -

1 Space Curves and Tangent Lines 2 Gradients and Tangent Planes
CLASS NOTES for CHAPTER 4, Nonlinear Programming 1 Space Curves and Tangent Lines Recall that space curves are de¯ned by a set of parametric equations, x1(t) 2 x2(t) 3 r(t) = . 6 . 7 6 7 6 xn(t) 7 4 5 In Calc III, we might have written this a little di®erently, ~r(t) =< x(t); y(t); z(t) > but here we want to use n dimensions rather than two or three dimensions. The derivative and antiderivative of r with respect to t is done component- wise, x10 (t) x1(t) dt 2 x20 (t) 3 2 R x2(t) dt 3 r(t) = . ; R(t) = . 6 . 7 6 R . 7 6 7 6 7 6 xn0 (t) 7 6 xn(t) dt 7 4 5 4 5 And the local linear approximation to r(t) is alsoRdone componentwise. The tangent line (in n dimensions) can be written easily- the derivative at t = a is the direction of the curve, so the tangent line is given by: x1(a) x10 (a) 2 x2(a) 3 2 x20 (a) 3 L(t) = . + t . 6 . 7 6 . 7 6 7 6 7 6 xn(a) 7 6 xn0 (a) 7 4 5 4 5 In Class Exercise: Use Maple to plot the curve r(t) = [cos(t); sin(t); t]T ¼ and its tangent line at t = 2 . 2 Gradients and Tangent Planes Let f : Rn R. In this case, we can write: ! y = f(x1; x2; x3; : : : ; xn) 1 Note that any function that we wish to optimize must be of this form- It would not make sense to ¯nd the maximum of a function like a space curve; n dimensional coordinates are not well-ordered like the real line- so the fol- lowing statement would be meaningless: (3; 5) > (1; 2). -

Leonhard Euler - Wikipedia, the Free Encyclopedia Page 1 of 14
Leonhard Euler - Wikipedia, the free encyclopedia Page 1 of 14 Leonhard Euler From Wikipedia, the free encyclopedia Leonhard Euler ( German pronunciation: [l]; English Leonhard Euler approximation, "Oiler" [1] 15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.[2] He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy. Euler spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He is considered to be the preeminent mathematician of the 18th century, and one of the greatest of all time. He is also one of the most prolific mathematicians ever; his collected works fill 60–80 quarto volumes. [3] A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is our teacher in all things," which has also been translated as "Read Portrait by Emanuel Handmann 1756(?) Euler, read Euler, he is the master of us all." [4] Born 15 April 1707 Euler was featured on the sixth series of the Swiss 10- Basel, Switzerland franc banknote and on numerous Swiss, German, and Died Russian postage stamps. The asteroid 2002 Euler was 18 September 1783 (aged 76) named in his honor. He is also commemorated by the [OS: 7 September 1783] Lutheran Church on their Calendar of Saints on 24 St. Petersburg, Russia May – he was a devout Christian (and believer in Residence Prussia, Russia biblical inerrancy) who wrote apologetics and argued Switzerland [5] forcefully against the prominent atheists of his time. -

The Legacy of Leonhard Euler: a Tricentennial Tribute (419 Pages)
P698.TP.indd 1 9/8/09 5:23:37 PM This page intentionally left blank Lokenath Debnath The University of Texas-Pan American, USA Imperial College Press ICP P698.TP.indd 2 9/8/09 5:23:39 PM Published by Imperial College Press 57 Shelton Street Covent Garden London WC2H 9HE Distributed by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. THE LEGACY OF LEONHARD EULER A Tricentennial Tribute Copyright © 2010 by Imperial College Press All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the Publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher. ISBN-13 978-1-84816-525-0 ISBN-10 1-84816-525-0 Printed in Singapore. LaiFun - The Legacy of Leonhard.pmd 1 9/4/2009, 3:04 PM September 4, 2009 14:33 World Scientific Book - 9in x 6in LegacyLeonhard Leonhard Euler (1707–1783) ii September 4, 2009 14:33 World Scientific Book - 9in x 6in LegacyLeonhard To my wife Sadhana, grandson Kirin,and granddaughter Princess Maya, with love and affection. -

Leonhard Euler's Elastic Curves Author(S): W
Leonhard Euler's Elastic Curves Author(s): W. A. Oldfather, C. A. Ellis and Donald M. Brown Source: Isis, Vol. 20, No. 1 (Nov., 1933), pp. 72-160 Published by: The University of Chicago Press on behalf of The History of Science Society Stable URL: http://www.jstor.org/stable/224885 Accessed: 10-07-2015 18:15 UTC Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at http://www.jstor.org/page/ info/about/policies/terms.jsp JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. The University of Chicago Press and The History of Science Society are collaborating with JSTOR to digitize, preserve and extend access to Isis. http://www.jstor.org This content downloaded from 128.138.65.63 on Fri, 10 Jul 2015 18:15:50 UTC All use subject to JSTOR Terms and Conditions LeonhardEuler's ElasticCurves (De Curvis Elasticis, Additamentum I to his Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes, Lausanne and Geneva, 1744). Translated and Annotated by W. A. OLDFATHER, C. A. ELLIS, and D. M. BROWN PREFACE In the fall of I920 Mr. CHARLES A. ELLIS, at that time Professor of Structural Engineering in the University of Illinois, called my attention to the famous appendix on elastic curves by LEONHARD EULER, which he felt might well be made available in an English translationto those students of structuralengineering who were interested in the classical treatises which constitute landmarks in the history of this ever increasingly important branch of scientific and technical achievement. -

2.8 the Derivative As a Function
2 Derivatives Copyright © Cengage Learning. All rights reserved. 2.8 The Derivative as a Function Copyright © Cengage Learning. All rights reserved. The Derivative as a Function We have considered the derivative of a function f at a fixed number a: Here we change our point of view and let the number a vary. If we replace a in Equation 1 by a variable x, we obtain 3 The Derivative as a Function Given any number x for which this limit exists, we assign to x the number f′(x). So we can regard f′ as a new function, called the derivative of f and defined by Equation 2. We know that the value of f′ at x, f′(x), can be interpreted geometrically as the slope of the tangent line to the graph of f at the point (x, f(x)). The function f′ is called the derivative of f because it has been “derived” from f by the limiting operation in Equation 2. The domain of f′ is the set {x | f′(x) exists} and may be smaller than the domain of f. 4 Example 1 – Derivative of a Function given by a Graph The graph of a function f is given in Figure 1. Use it to sketch the graph of the derivative f′. Figure 1 5 Example 1 – Solution We can estimate the value of the derivative at any value of x by drawing the tangent at the point (x, f(x)) and estimating its slope. For instance, for x = 5 we draw the tangent at P in Figure 2(a) and estimate its slope to be about , so f′(5) ≈ 1.5. -
![Arxiv:2103.13478V2 [Math.NT] 11 May 2021 Solution of the Differential Equation Y = E , Special Values of Bell Polynomials](https://docslib.b-cdn.net/cover/8988/arxiv-2103-13478v2-math-nt-11-may-2021-solution-of-the-differential-equation-y-e-special-values-of-bell-polynomials-1978988.webp)
Arxiv:2103.13478V2 [Math.NT] 11 May 2021 Solution of the Differential Equation Y = E , Special Values of Bell Polynomials
Solution of the Differential Equation y(k) = eay, Special Values of Bell Polynomials and (k,a)-Autonomous Coefficients Ronald Orozco L´opez Departamento de Matem´aticas Universidad de los Andes Bogot´a, 111711 Colombia [email protected] Abstract In this paper special values of Bell polynomials are given by using the power series solution of the equation y(k) = eay. In addition, complete and partial exponential autonomous functions, exponential autonomous polyno- mials, autonomous polynomials and (k, a)-autonomous coefficients are de- fined. Finally, we show the relationship between various numbers counting combinatorial objects and binomial coefficients, Stirling numbers of second kind and autonomous coefficients. 1 Introduction It is a known fact that Bell polynomials are closely related to derivatives of composi- tion of functions. For example, Faa di Bruno [5], Foissy [6], and Riordan [10] showed that Bell polynomials are a very useful tool in mathematics to represent the n-th derivative of the composition of functions. Also, Bernardini and Ricci [2], Yildiz et arXiv:2103.13478v2 [math.NT] 11 May 2021 al. [12], Caley [3], and Wang [13] showed the relationship between Bell polynomials and differential equations. On the other hand, Orozco [9] studied the convergence of the analytic solution of the autonomous differential equation y(k) = f(y) by using Faa di Bruno’s formula. We can then look at differential equations as a source for investigating special values of Bell polynomials. In this paper we will focus on finding special values of Bell polynomials when the vector field f(x) of the autonomous differential equation y(k) = f(y) is the exponential function. -

3.5 Leibniz's Fundamental Theorem of Calculus
3.5 Leibniz’s Fundamental Theorem of Calculus 133 spherical surface on top of the ice-cream cone. You may use knowledge of the surface area of the entire sphere, which Archimedes had determined. Exercise 3.24: Imagine boring a round hole through the center of a sphere, leaving a spherical ring. Use the result of Exercise 3.23 to find the volume of the ring. Hint: Amazingly, your answer should depend only on the height of the ring, not the size of the original sphere. Also obtain your result directly from Cavalieri’s Principle by comparing the ring with a sphere of diameter the height of the ring. 3.5 Leibniz’s Fundamental Theorem of Calculus Gottfried Wilhelm Leibniz and Isaac Newton were geniuses who lived quite different lives and invented quite different versions of the infinitesimal calculus, each to suit his own interests and purposes. Newton discovered his fundamental ideas in 1664–1666, while a student at Cambridge University. During a good part of these years the Univer- sity was closed due to the plague, and Newton worked at his family home in Woolsthorpe, Lincolnshire. However, his ideas were not published until 1687. Leibniz, in France and Germany, on the other hand, began his own breakthroughs in 1675, publishing in 1684. The importance of publication is illustrated by the fact that scientific communication was still sufficiently uncoordinated that it was possible for the work of Newton and Leibniz to proceed independently for many years without reciprocal knowledge and input. Disputes about the priority of their discoveries raged for centuries, fed by nationalistic tendencies in England and Germany.