DOCSLIB.ORG

Convex Polytopes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Convex Polytopes Convex Polytopes The early history of convex polytopes is lost. About 2000 BC convex polytopes appeared in a mathematical context in the Sumerian civilization, in Babylonia and in Egypt. Sources are the Moscow papyrus and the Rhind papyrus. Some of the regular polytopes were already known by then. A basic problem was to calculate the vol- umes of truncated pyramids. This was needed to determine the number of bricks for fortifications and buildings. Babylonians sometimes did the calculations correctly, sometimes not, while Egyptians used the right formula. For pertinent information the author is obliged to the assyriologist Hermann Hunger [531]. In the fifth century BC Democritos also discovered this formula and Eudoxos proved it, using the method of exhaustion. Theaitetos developed a theory of regular polytopes, later treated by Plato in the dialogue Timaios. Euclid, around 300 BC, considered metric proper- ties of polytopes, the volume problem, including the exhaustion method, and the five regular polytopes, the Platonic solids. Zenodoros, who lived sometime between 200 BC and 90 AD, studied the isoperimetric problem for polygons and polytopes and Pappos, about 300 AD, dealt with the semi-regular polytopes of Archimedes. In the renaissance the study of convex polytopes was in the hands of artists such as Uccello, Pacioli, da Vinci, D¨urer, and Jamnitzer. Then it went back to mathe- matics. Kepler investigated the regular and the semi-regular polytopes and planar tilings. Descartes considered convex polytopes from a metric point of view, almost arriving at Euler’s polytope formula, discovered by Euler only hundred years later. Contributions to polytope theory in the late eighteenth and the nineteenth century are due to Legendre, Cauchy, Steiner, Schlafli¨ and others. At the turn of the nine- teenth and in the twentieth century important results were given by Minkowski, Dehn, Sommerville, Steinitz, Coxeter and numerous contemporaries. At present, emphasis is on the combinatorial, algorithmic, and algebraic aspects. Modern rela- tions to other areas date back to Newton (polynomials), Fourier (linear optimization), Dirichlet, Minkowski and Vorono˘ı(quadraticforms)andFedorov(crystallography). In recent decades polytope theory was strongly stimulated and, in part, re-oriented by linear optimization, computer science and algebraic geometry. Polytope theory, in turn, had a certain impact on these areas. For the history, see Federico [318] and Malkevitch [681]. 244 Convex Polytopes The material in this chapter is arranged as follows. After some preliminaries and the introduction of the face lattice, combinatorial properties of convex poly- topes are considered, beginning with Euler’s polytope formula. In Sect. 14 we treat the elementary volume as a valuation, and Hilbert’s third problem. Next, Cauchy’s rigidity theorem for polytopal convex surfaces and rigidity of frameworks are dis- cussed. Then classical results of Minkowski, Alexandrov and Lindelof¨ are studied. Lindelof’s¨ results deals with the isoperimetric problem for polytopes. Section 14 treats lattice polytopes, including results of Ehrhart, Reeve and Macdonald and the Betke–Kneser valuation theorem. Applications of lattice polytopes deal with irre- ducibility of polynomials and the Minding–Bernstein theorem on the number of zeros of systems of polynomial equations. Finally we present an account of linear optimization, including aspects of integer linear optimization. For additional material the reader may wish to consult the books of Alexan- drov [16], Gr¨unbaum [453], McMullen and Shephard [718], Brøndsted [171], Ewald [315] and Ziegler [1045], the survey of Bayer and Lee [83] and other surveys in the Handbooks of Convex Geometry [475] and Discrete and Computational Geome- try [476]. Regular polytopes and related topics will not be considered. For these we refer to Coxeter [230, 232], Robertson [842], McMullen and Schulte [717] and Johnson [551]. For McMullen’s algebra of polytopes, see [713]. 14 Preliminaries and the Face Lattice The simple concept of a convex polytope embodies a wealth of mathematical struc- ture and problems and, consequently, yields numerous results. The elementary theory of convex polytopes deals with faces and normal cones, duality, in particular polarity, separation and other simple notions. It was developed in the late eighteenth, the nine- teenth and the early twentieth century. Some of the results are difficult to attribute. In part this is due to the large number of contributors. In this section we first give basic definitions, and then show the equivalence of the notions of V-polytopes and H-polytopes and, similarly, of V-andH-polyhedra. We conclude with a short study of the face lattice of a convex polytope using polarity. For more information, see the books cited earlier, to which we add Schneider [907] and Schrijver [915]. 14.1 Basic Concepts and Simple Properties of Convex Polytopes In the following we introduce the notion of convex polytopes and describe two alternative ways to specify convex polytopes: as convex hulls (V-polytopes) and as intersections of halfspaces (H-polytopes). An example deals with a result of Gauss on zeros of polynomials. 14 Preliminaries and the Face Lattice 245 Convex Polytopes and Faces A convex polytope P in Ed is the convex hull of a finite, possibly empty, set in d E .IfP conv x1,...,xn ,thentheextremepointsofP are among the points = { } x1,...,xn by Minkowski’s theorem 5.5 on extreme points. Thus, a convex polytope has only finitely many extreme points. If, conversely, a convex body has only finitely many extreme points, then it is the convex hull of these, again by Minkowski’s theo- rem. Hence, the convex polytopes are precisely the convex bodies with finitely many extreme points. The intersection of P with a support hyperplane H is a face of P.It is not difficult to prove that (1) H P conv(H x1,...,xn ). ∩ = ∩{ } This shows that a face of P is again a convex polytope. The faces of dimension 0 are the vertices of P.Thesearepreciselytheextreme,actuallytheexposedpointsofP. The faces of dimension 1 are the edges of P and the faces of dimension dim P 1the facets.Theemptyset and P itself are called the improper faces,allotherfacesare− ∅ proper.SinceafaceofP is the convex hull of those points among x1,...,xn which are contained in it, P has only finitely many faces. Since each boundary point of P is contained in a support hyperplane by Theorem 4.1, bd P is the union of all proper faces of P.ByF(P) we mean the family of all faces of P,including and P.The d d ∅ d space of all convex polytopes in E is denoted by (E ) and p p(E ) is its sub-space consisting of all proper convex polytopes,P = P that is thoseP with= non-emptyP interior. Gauss’s Theorem on the Zeros of the Derivative of a Polynomial In an appendix to his third proof of the fundamental theorem of algebra, Gauss [363] proved the following result. Theorem 14.1. Let p be a polynomial in one complex variable. Then the zeros of its derivative p$ are contained in the convex polygon determined by the zeros of p. Proof. Let z1,...,zn C be the zeros of p,eachwrittenaccordingtoitsmultiplic- ity. Then ∈ p(z) a(z z1) (z zn) for z C = − ··· − ∈ with suitable a C.Letz z1,...,zn.Dividingthederivativep$(z) by p(z) implies that ∈ &= p$(z) 1 1 z z1 z zn (2) ¯ −¯ 2 ¯ −¯ 2 . p(z) = z z1 +···+ z zn = z z1 +···+ z zn − − | − | | − | Assume now that z is a zero of p .Wehavetoshowthatz conv z1,...,zn .Ifz $ ∈ { } is equal to one of z1,...,zn,thisholdstrivially.Otherwise(2)showsthat 1 1 2 z1 2 zn z z1 z zn | − | +···+ | − | z 1 1 . = 2 2 z z1 z zn | − | +···+ | − | Thus z is a convex combination of z1,...,zn. '( 246 Convex Polytopes V-Polytopes and H-Polytopes Convex polytopes as defined earlier are also called convex V-polytopes.HereV stands for vertices. Dually, a convex H-polyhedron is the intersection of finitely many closed halfspaces. A bounded convex H-polyhedron is called a convex H-polytope. AformalproofofthefollowingfolktheoremisduetoWeyl[1021],seealso Minkowski [744], Sect. 4. Theorem 14.2. Let P Ed .Thenthefollowingstatementsareequivalent: ⊆ (i) PisaconvexV-polytope. (ii) PisaconvexH-polytope. Proof. (i) (ii) We may suppose that dim P d. P has only finitely many faces. Since each⇒ boundary point of P is contained in= a support hyperplane of P by Theo- rem 4.1, bd P is the union of its proper faces. Connecting an interior point of P with alinesegmentwhichmissesallfacesofdimensionatmostd 2withanexterior point, each point where it intersects the boundary of P must be− contained in a face of dimension d 1, i.e. in a facet. Thus P must have facets. Let Hi , i 1,...,m, − = be the hyperplanes containing the facets of P and Hi− the corresponding support halfspaces. We claim that (3) P H − H −. = 1 ∩···∩ m The inclusion P H − H is trivial. To show the reverse inclusion, let ⊆ 1 ∩···∩ m− x Ed P.ForeachofthefinitelymanyfacesofP of dimension at most d 2, consider∈ \ the affine hull of the face and x.Chooseapointy int P which is contained− in none of these affine hulls. The intersection of the line∈ segment x, y with bd P then is a point z bd P which is contained in none of these affine hulls[ ] and thus in none of the faces∈ of P of dimension at most d 2. Since bd P is the union of all − faces, z is contained in a suitable facet and thus in one of the hyperplanes, say Hi . Then x Hi− and therefore x H1− Hm−.HenceP H1− Hm−, concluding&∈ the proof of (3). &∈ ∩···∩ ⊇ ∩···∩ (ii) (i) Let P H − H be bounded, where each H −, i 1, , m, ⇒ = 1 ∩···∩ m− i = ··· is a halfspace with boundary hyperplane Hi . Clearly, P is a convex body. By Minkowski’s theorem 5.5, P is the convex hull of its extreme points.
Load more

Recommended publications
  • Lecture 3 1 Geometry of Linear Programs
    ORIE 6300 Mathematical Programming I September 2, 2014 Lecture 3 Lecturer: David P. Williamson Scribe: Divya Singhvi Last time we discussed how to take dual of an LP in two different ways. Today we will talk about the geometry of linear programs. 1 Geometry of Linear Programs First we need some definitions. Definition 1 A set S ⊆ <n is convex if 8x; y 2 S, λx + (1 − λ)y 2 S, 8λ 2 [0; 1]. Figure 1: Examples of convex and non convex sets Given a set of inequalities we define the feasible region as P = fx 2 <n : Ax ≤ bg. We say that P is a polyhedron. Which points on this figure can have the optimal value? Our intuition from last time is that Figure 2: Example of a polyhedron. \Circled" corners are feasible and \squared" are non feasible optimal solutions to linear programming problems occur at \corners" of the feasible region. What we'd like to do now is to consider formal definitions of the \corners" of the feasible region. 3-1 One idea is that a point in the polyhedron is a corner if there is some objective function that is minimized there uniquely. Definition 2 x 2 P is a vertex of P if 9c 2 <n with cT x < cT y; 8y 6= x; y 2 P . Another idea is that a point x 2 P is a corner if there are no small perturbations of x that are in P . Definition 3 Let P be a convex set in <n. Then x 2 P is an extreme point of P if x cannot be written as λy + (1 − λ)z for y; z 2 P , y; z 6= x, 0 ≤ λ ≤ 1.
    [Show full text]
  • Descartes, Euler, Poincaré, Pólya and Polyhedra Séminaire De Philosophie Et Mathématiques, 1982, Fascicule 8 « Descartes, Euler, Poincaré, Polya and Polyhedra », , P
    Séminaire de philosophie et mathématiques PETER HILTON JEAN PEDERSEN Descartes, Euler, Poincaré, Pólya and Polyhedra Séminaire de Philosophie et Mathématiques, 1982, fascicule 8 « Descartes, Euler, Poincaré, Polya and Polyhedra », , p. 1-17 <http://www.numdam.org/item?id=SPHM_1982___8_A1_0> © École normale supérieure – IREM Paris Nord – École centrale des arts et manufactures, 1982, tous droits réservés. L’accès aux archives de la série « Séminaire de philosophie et mathématiques » implique l’accord avec les conditions générales d’utilisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ - 1 - DESCARTES, EULER, POINCARÉ, PÓLYA—AND POLYHEDRA by Peter H i l t o n and Jean P e d e rs e n 1. Introduction When geometers talk of polyhedra, they restrict themselves to configurations, made up of vertices. edqes and faces, embedded in three-dimensional Euclidean space. Indeed. their polyhedra are always homeomorphic to thè two- dimensional sphere S1. Here we adopt thè topologists* terminology, wherein dimension is a topological invariant, intrinsic to thè configuration. and not a property of thè ambient space in which thè configuration is located. Thus S 2 is thè surface of thè 3-dimensional ball; and so we find. among thè geometers' polyhedra. thè five Platonic “solids”, together with many other examples. However. we should emphasize that we do not here think of a Platonic “solid” as a solid : we have in mind thè bounding surface of thè solid.
    [Show full text]
  • Computational Geometry – Problem Session Convex Hull & Line Segment Intersection
    Computational Geometry { Problem Session Convex Hull & Line Segment Intersection LEHRSTUHL FUR¨ ALGORITHMIK · INSTITUT FUR¨ THEORETISCHE INFORMATIK · FAKULTAT¨ FUR¨ INFORMATIK Guido Bruckner¨ 04.05.2018 Guido Bruckner¨ · Computational Geometry { Problem Session Modus Operandi To register for the oral exam we expect you to present an original solution for at least one problem in the exercise session. • this is about working together • don't worry if your idea doesn't work! Guido Bruckner¨ · Computational Geometry { Problem Session Outline Convex Hull Line Segment Intersection Guido Bruckner¨ · Computational Geometry { Problem Session Definition of Convex Hull Def: A region S ⊆ R2 is called convex, when for two points p; q 2 S then line pq 2 S. The convex hull CH(S) of S is the smallest convex region containing S. Guido Bruckner¨ · Computational Geometry { Problem Session Definition of Convex Hull Def: A region S ⊆ R2 is called convex, when for two points p; q 2 S then line pq 2 S. The convex hull CH(S) of S is the smallest convex region containing S. Guido Bruckner¨ · Computational Geometry { Problem Session Definition of Convex Hull Def: A region S ⊆ R2 is called convex, when for two points p; q 2 S then line pq 2 S. The convex hull CH(S) of S is the smallest convex region containing S. In physics: Guido Bruckner¨ · Computational Geometry { Problem Session Definition of Convex Hull Def: A region S ⊆ R2 is called convex, when for two points p; q 2 S then line pq 2 S. The convex hull CH(S) of S is the smallest convex region containing S.
    [Show full text]
  • A General Geometric Construction of Coordinates in a Convex Simplicial Polytope
    A general geometric construction of coordinates in a convex simplicial polytope ∗ Tao Ju a, Peter Liepa b Joe Warren c aWashington University, St. Louis, USA bAutodesk, Toronto, Canada cRice University, Houston, USA Abstract Barycentric coordinates are a fundamental concept in computer graphics and ge- ometric modeling. We extend the geometric construction of Floater’s mean value coordinates [8,11] to a general form that is capable of constructing a family of coor- dinates in a convex 2D polygon, 3D triangular polyhedron, or a higher-dimensional simplicial polytope. This family unifies previously known coordinates, including Wachspress coordinates, mean value coordinates and discrete harmonic coordinates, in a simple geometric framework. Using the construction, we are able to create a new set of coordinates in 3D and higher dimensions and study its relation with known coordinates. We show that our general construction is complete, that is, the resulting family includes all possible coordinates in any convex simplicial polytope. Key words: Barycentric coordinates, convex simplicial polytopes 1 Introduction In computer graphics and geometric modelling, we often wish to express a point x as an affine combination of a given point set vΣ = {v1,...,vi,...}, x = bivi, where bi =1. (1) i∈Σ i∈Σ Here bΣ = {b1,...,bi,...} are called the coordinates of x with respect to vΣ (we shall use subscript Σ hereafter to denote a set). In particular, bΣ are called barycentric coordinates if they are non-negative. ∗ [email protected] Preprint submitted to Elsevier Science 3 December 2006 v1 v1 x x v4 v2 v2 v3 v3 (a) (b) Fig.
    [Show full text]
  • 1 Lifts of Polytopes
    Lecture 5: Lifts of polytopes and non-negative rank CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016 1 Lifts of polytopes 1.1 Polytopes and inequalities Recall that the convex hull of a subset X n is defined by ⊆ conv X λx + 1 λ x0 : x; x0 X; λ 0; 1 : ( ) f ( − ) 2 2 [ ]g A d-dimensional convex polytope P d is the convex hull of a finite set of points in d: ⊆ P conv x1;:::; xk (f g) d for some x1;:::; xk . 2 Every polytope has a dual representation: It is a closed and bounded set defined by a family of linear inequalities P x d : Ax 6 b f 2 g for some matrix A m d. 2 × Let us define a measure of complexity for P: Define γ P to be the smallest number m such that for some C s d ; y s ; A m d ; b m, we have ( ) 2 × 2 2 × 2 P x d : Cx y and Ax 6 b : f 2 g In other words, this is the minimum number of inequalities needed to describe P. If P is full- dimensional, then this is precisely the number of facets of P (a facet is a maximal proper face of P). Thinking of γ P as a measure of complexity makes sense from the point of view of optimization: Interior point( methods) can efficiently optimize linear functions over P (to arbitrary accuracy) in time that is polynomial in γ P . ( ) 1.2 Lifts of polytopes Many simple polytopes require a large number of inequalities to describe.
    [Show full text]
  • The Orientability of Small Covers and Coloring Simple Polytopes
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Osaka City University Repository Nakayama, H. and Nishimura, Y. Osaka J. Math. 42 (2005), 243–256 THE ORIENTABILITY OF SMALL COVERS AND COLORING SIMPLE POLYTOPES HISASHI NAKAYAMA and YASUZO NISHIMURA (Received September 1, 2003) Abstract Small Cover is an -dimensional manifold endowed with a Z2 action whose or- bit space is a simple convex polytope . It is known that a small cover over is characterized by a coloring of which satisfies a certain condition. In this paper we shall investigate the topology of small covers by the coloring theory in com- binatorics. We shall first give an orientability condition for a small cover. In case = 3, an orientable small cover corresponds to a four colored polytope. The four color theorem implies the existence of orientable small cover over every simple con- vex 3-polytope. Moreover we shall show the existence of non-orientable small cover over every simple convex 3-polytope, except the 3-simplex. 0. Introduction “Small Cover” was introduced and studied by Davis and Januszkiewicz in [5]. It is a real version of “Quasitoric manifold,” i.e., an -dimensional manifold endowed with an action of the group Z2 whose orbit space is an -dimensional simple convex poly- tope. A typical example is provided by the natural action of Z2 on the real projec- tive space R whose orbit space is an -simplex. Let be an -dimensional simple convex polytope. Here is simple if the number of codimension-one faces (which are called “facets”) meeting at each vertex is , equivalently, the dual of its boundary complex ( ) is an ( 1)-dimensional simplicial sphere.
    [Show full text]
  • Archimedean Solids
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Anderson, Anna, "Archimedean Solids" (2008). MAT Exam Expository Papers. 4. https://digitalcommons.unl.edu/mathmidexppap/4 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Archimedean Solids Anna Anderson In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 2 Archimedean Solids A polygon is a simple, closed, planar figure with sides formed by joining line segments, where each line segment intersects exactly two others. If all of the sides have the same length and all of the angles are congruent, the polygon is called regular. The sum of the angles of a regular polygon with n sides, where n is 3 or more, is 180° x (n – 2) degrees. If a regular polygon were connected with other regular polygons in three dimensional space, a polyhedron could be created. In geometry, a polyhedron is a three- dimensional solid which consists of a collection of polygons joined at their edges. The word polyhedron is derived from the Greek word poly (many) and the Indo-European term hedron (seat).
    [Show full text]
  • Euler Characteristics, Gauss-Bonnett, and Index Theorems
    EULER CHARACTERISTICS,GAUSS-BONNETT, AND INDEX THEOREMS Keefe Mitman and Matthew Lerner-Brecher Department of Mathematics; Columbia University; New York, NY 10027; UN3952, Song Yu. Keywords Euler Characteristics, Gauss-Bonnett, Index Theorems. Contents 1 Foreword 1 2 Euler Characteristics 2 2.1 Introduction . 2 2.2 Betti Numbers . 2 2.2.1 Chains and Boundary Operators . 2 2.2.2 Cycles and Homology . 3 2.3 Euler Characteristics . 4 3 Gauss-Bonnet Theorem 4 3.1 Background . 4 3.2 Examples . 5 4 Index Theorems 6 4.1 The Differential of a Manifold Map . 7 4.2 Degree and Index of a Manifold Map . 7 4.2.1 Technical Definition . 7 4.2.2 A More Concrete Case . 8 4.3 The Poincare-Hopf Theorem and Applications . 8 1 Foreword Within this course thus far, we have become rather familiar with introductory differential geometry, complexes, and certain applications of complexes. Unfortunately, however, many of the geometries we have been discussing remain MARCH 8, 2019 fairly arbitrary and, so far, unrelated, despite their underlying and inherent similarities. As a result of this discussion, we hope to unearth some of these relations and make the ties between complexes in applied topology more apparent. 2 Euler Characteristics 2.1 Introduction In mathematics we often find ourselves concerned with the simple task of counting; e.g., cardinality, dimension, etcetera. As one might expect, with differential geometry the story is no different. 2.2 Betti Numbers 2.2.1 Chains and Boundary Operators Within differential geometry, we count using quantities known as Betti numbers, which can easily be related to the number of n-simplexes in a complex, as we will see in the subsequent discussion.
    [Show full text]
  • 0.1 Euler Characteristic
    0.1 Euler Characteristic Definition 0.1.1. Let X be a finite CW complex of dimension n and denote by ci the number of i-cells of X. The Euler characteristic of X is defined as: n X i χ(X) = (−1) · ci: (0.1.1) i=0 It is natural to question whether or not the Euler characteristic depends on the cell structure chosen for the space X. As we will see below, this is not the case. For this, it suffices to show that the Euler characteristic depends only on the cellular homology of the space X. Indeed, cellular homology is isomorphic to singular homology, and the latter is independent of the cell structure on X. Recall that if G is a finitely generated abelian group, then G decomposes into a free part and a torsion part, i.e., r G ' Z × Zn1 × · · · Znk : The integer r := rk(G) is the rank of G. The rank is additive in short exact sequences of finitely generated abelian groups. Theorem 0.1.2. The Euler characteristic can be computed as: n X i χ(X) = (−1) · bi(X) (0.1.2) i=0 with bi(X) := rk Hi(X) the i-th Betti number of X. In particular, χ(X) is independent of the chosen cell structure on X. Proof. We use the following notation: Bi = Image(di+1), Zi = ker(di), and Hi = Zi=Bi. Consider a (finite) chain complex of finitely generated abelian groups and the short exact sequences defining homology: dn+1 dn d2 d1 d0 0 / Cn / ::: / C1 / C0 / 0 ι di 0 / Zi / Ci / / Bi−1 / 0 di+1 q 0 / Bi / Zi / Hi / 0 The additivity of rank yields that ci := rk(Ci) = rk(Zi) + rk(Bi−1) and rk(Zi) = rk(Bi) + rk(Hi): Substitute the second equality into the first, multiply the resulting equality by (−1)i, and Pn i sum over i to get that χ(X) = i=0(−1) · rk(Hi).
    [Show full text]
  • On the Ekeland Variational Principle with Applications and Detours
    Lectures on The Ekeland Variational Principle with Applications and Detours By D. G. De Figueiredo Tata Institute of Fundamental Research, Bombay 1989 Author D. G. De Figueiredo Departmento de Mathematica Universidade de Brasilia 70.910 – Brasilia-DF BRAZIL c Tata Institute of Fundamental Research, 1989 ISBN 3-540- 51179-2-Springer-Verlag, Berlin, Heidelberg. New York. Tokyo ISBN 0-387- 51179-2-Springer-Verlag, New York. Heidelberg. Berlin. Tokyo No part of this book may be reproduced in any form by print, microfilm or any other means with- out written permission from the Tata Institute of Fundamental Research, Colaba, Bombay 400 005 Printed by INSDOC Regional Centre, Indian Institute of Science Campus, Bangalore 560012 and published by H. Goetze, Springer-Verlag, Heidelberg, West Germany PRINTED IN INDIA Preface Since its appearance in 1972 the variational principle of Ekeland has found many applications in different fields in Analysis. The best refer- ences for those are by Ekeland himself: his survey article [23] and his book with J.-P. Aubin [2]. Not all material presented here appears in those places. Some are scattered around and there lies my motivation in writing these notes. Since they are intended to students I included a lot of related material. Those are the detours. A chapter on Nemyt- skii mappings may sound strange. However I believe it is useful, since their properties so often used are seldom proved. We always say to the students: go and look in Krasnoselskii or Vainberg! I think some of the proofs presented here are more straightforward. There are two chapters on applications to PDE.
    [Show full text]
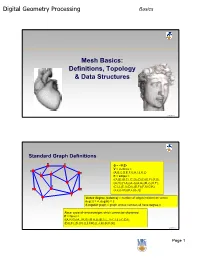
  • Digital Geometry Processing Mesh Basics
    Digital Geometry Processing Basics Mesh Basics: Definitions, Topology & Data Structures 1 © Alla Sheffer Standard Graph Definitions G = <V,E> V = vertices = {A,B,C,D,E,F,G,H,I,J,K,L} E = edges = {(A,B),(B,C),(C,D),(D,E),(E,F),(F,G), (G,H),(H,A),(A,J),(A,G),(B,J),(K,F), (C,L),(C,I),(D,I),(D,F),(F,I),(G,K), (J,L),(J,K),(K,L),(L,I)} Vertex degree (valence) = number of edges incident on vertex deg(J) = 4, deg(H) = 2 k-regular graph = graph whose vertices all have degree k Face: cycle of vertices/edges which cannot be shortened F = faces = {(A,H,G),(A,J,K,G),(B,A,J),(B,C,L,J),(C,I,L),(C,D,I), (D,E,F),(D,I,F),(L,I,F,K),(L,J,K),(K,F,G)} © Alla Sheffer Page 1 Digital Geometry Processing Basics Connectivity Graph is connected if there is a path of edges connecting every two vertices Graph is k-connected if between every two vertices there are k edge-disjoint paths Graph G’=<V’,E’> is a subgraph of graph G=<V,E> if V’ is a subset of V and E’ is the subset of E incident on V’ Connected component of a graph: maximal connected subgraph Subset V’ of V is an independent set in G if the subgraph it induces does not contain any edges of E © Alla Sheffer Graph Embedding Graph is embedded in Rd if each vertex is assigned a position in Rd Embedding in R2 Embedding in R3 © Alla Sheffer Page 2 Digital Geometry Processing Basics Planar Graphs Planar Graph Plane Graph Planar graph: graph whose vertices and edges can Straight Line Plane Graph be embedded in R2 such that its edges do not intersect Every planar graph can be drawn as a straight-line plane graph ©
    [Show full text]
  • Recognizing Surfaces
    RECOGNIZING SURFACES Ivo Nikolov and Alexandru I. Suciu Mathematics Department College of Arts and Sciences Northeastern University Abstract The subject of this poster is the interplay between the topology and the combinatorics of surfaces. The main problem of Topology is to classify spaces up to continuous deformations, known as homeomorphisms. Under certain conditions, topological invariants that capture qualitative and quantitative properties of spaces lead to the enumeration of homeomorphism types. Surfaces are some of the simplest, yet most interesting topological objects. The poster focuses on the main topological invariants of two-dimensional manifolds—orientability, number of boundary components, genus, and Euler characteristic—and how these invariants solve the classification problem for compact surfaces. The poster introduces a Java applet that was written in Fall, 1998 as a class project for a Topology I course. It implements an algorithm that determines the homeomorphism type of a closed surface from a combinatorial description as a polygon with edges identified in pairs. The input for the applet is a string of integers, encoding the edge identifications. The output of the applet consists of three topological invariants that completely classify the resulting surface. Topology of Surfaces Topology is the abstraction of certain geometrical ideas, such as continuity and closeness. Roughly speaking, topol- ogy is the exploration of manifolds, and of the properties that remain invariant under continuous, invertible transforma- tions, known as homeomorphisms. The basic problem is to classify manifolds according to homeomorphism type. In higher dimensions, this is an impossible task, but, in low di- mensions, it can be done. Surfaces are some of the simplest, yet most interesting topological objects.
    [Show full text]