Arithmetic Optimization Using Carry-Save-Adders
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Digital Electronic Circuits
DIGITAL ELECTRONIC CIRCUITS SUBJECT CODE: PEI4I103 B.Tech, Fourth Semester Prepared By Dr. Kanhu Charan Bhuyan Asst. Professor Instrumentation and Electronics Engineering COLLEGE OF ENGINEERING AND TECHNOLOGY BHUBANESWAR B.Tech (E&IE/AE&I) detail Syllabus for Admission Batch 2015-16 PEI4I103- DIGITAL ELECTRONICS University level 80% MODULE – I (12 Hours)1. Number System: Introduction to various number systems and their Conversion. Arithmetic Operation using 1’s and 2`s Compliments, Signed Binary and Floating Point Number Representation Introduction to Binary codes and their applications. (5 Hours) 2. Boolean Algebra and Logic Gates: Boolean algebra and identities, Complete Logic set, logic gates and truth tables. Universal logic gates, Algebraic Reduction and realization using logic gates (3 Hours) 3. Combinational Logic Design: Specifying the Problem, Canonical Logic Forms, Extracting Canonical Forms, EX-OR Equivalence Operations, Logic Array, K-Maps: Two, Three and Four variable K-maps, NAND and NOR Logic Implementations. (4 Hours) MODULE – II (14 Hours) 4. Logic Components: Concept of Digital Components, Binary Adders, Subtraction and Multiplication, An Equality Detector and comparator, Line Decoder, encoders, Multiplexers and De-multiplexers. (5 Hours) 5. Synchronous Sequential logic Design: sequential circuits, storage elements: Latches (SR,D), Storage elements: Flip-Flops inclusion of Master-Slave, characteristics equation and state diagram of each FFs and Conversion of Flip-Flops. Analysis of Clocked Sequential circuits and Mealy and Moore Models of Finite State Machines (6 Hours) 6. Binary Counters: Introduction, Principle and design of synchronous and asynchronous counters, Design of MOD-N counters, Ring counters. Decade counters, State Diagram of binary counters (4 hours) MODULE – III (12 hours) 7. -

Design and Analysis of Power Efficient PTL Half Subtractor Using 120Nm Technology
International Journal of Computer Trends and Technology (IJCTT) – volume 7 number 4– Jan 2014 Design and Analysis of Power Efficient PTL Half Subtractor Using 120nm Technology 1 2 Pranshu Sharma , Anjali Sharma 1(Department of Electronics & Communication Engineering, APG Shimla University, India) 2(Department of Electronics & Communication Engineering, APG Shimla University, India) ABSTRACT : In the designing of any VLSI System, There are a number of logic styles by which a circuit can arithmetic circuits play a vital role, subtractor circuit is be implemented some of them used in this paper are one among them. In this paper a Power efficient Half- CMOS, TG, PTL. CMOS logic styles are robust against Subtractor has been designed using the PTL technique. voltage scaling and transistor sizing and thus provide a Subtractor circuit using this technique consumes less reliable operation at low voltages and arbitrary transistor power in comparison to the CMOS and TG techniques. sizes. In CMOS style input signals are connected to The proposed Half-Subtractor circuit using the PTL transistor gates only, which facilitate the usage and technique consists of 6 NMOS and 4 PMOS. The characterization of logic cells. Due to the complementary proposed PTL Half-Subtractor is designed and simulated transistor pairs the layout of CMOS gates is not much using DSCH 3.1 and Microwind 3.1 on 120nm. The complicated and is power efficient. The large number of power estimation and simulation of layout has been done PMOS transistors used in complementary CMOS logic for the proposed PTL half-Subtractor design. Power style is one of its major disadvantages and it results in comparison on BSIM-4 and LEVEL-3 has been high input loads [3]. -

Design of Adder / Subtractor Circuits Based On
ISSN (Print) : 2320 – 3765 ISSN (Online): 2278 – 8875 International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering (An ISO 3297: 2007 Certified Organization) Vol. 2, Issue 8, August 2013 DESIGN OF ADDER / SUBTRACTOR CIRCUITS BASED ON REVERSIBLE GATES V.Kamalakannan1, Shilpakala.V2, Ravi.H.N3 Lecturer, Department of ECE, R.L.Jalappa Institute of Technology, Doddaballapur, Karnataka, India 1 Asst. Professor & HOD, Department of ECE, R.L.Jalappa Institute of Technology, Doddaballapur, Karnataka, India2 Lab Assistant, Dept. of ECE, U.V.C.E, Bangalore Karnataka, India3 ABSTRACT: Reversible logic has extensive applications in quantum computing, it is a unconventional form of computing where the computational process is reversible, i.e., time-invertible. The main motivation behind the study of this technology is aimed at implementing reversible computing where they offer what is predicted to be the only potential way to improve the energy efficiency of computers beyond von Neumann-Landauer limit. It is relatively new and emerging area in the field of computing that taught us to think physically about computation Quantum Computing will be a total change in how the computer will operate and function. The reversible arithmetic circuits are efficient in terms of number of reversible gates, garbage output and quantum cost. In this paper design Reversible Binary Adder- Subtractor- Mux, Adder-Subtractor- TR Gate., Adder-Subtractor- Hybrid are proposed. In all the three design approaches, the Adder and Subtractor are realized in a single unit as compared to only full adder/subtractor in the existing design. The performance analysis is verified using number reversible gates, Garbage input/outputs and Quantum Cost.The reversible 4-bit full adder/ subtractor design unit is compared with conventional ripple carry adder, carry look ahead adder, carry skip adder, Manchester carry adder based on their performance with respect to area, timing and power. -

Area and Power Optimized D-Flip Flop and Subtractor
IT in Industry, Vol. 9, No.1, 2021 Published Online 28-02-2021 AREA AND POWER OPTIMIZED D-FLIP FLOP AND SUBTRACTOR T. Subhashini1, M. Kamaraju2, K. Babulu3 1,2 Department of ECE, Gudlavalleru Engineering College, India 3Department of ECE, UCOE, JNTUK, Kakinada, India Abstract: Low power is essential in today’s technology. It LITERATURE SURVEY is most significant with high speed, small size and stability. So, power reduction is most important in modern In the era of microelectronics, power dissipation is technology using VLSI design techniques. Today most of limiting factor. In any CMOS technology, provides the market necessities require low power, long run time very low Static power dissipation. Due to the and market which also deserve small size and high speed. discharge of capacitance, during the switching In this paper several logic circuits DFF with 5 transistors operation, that cause a power dissipation. Which and sub tractor circuit using powerless XOR gate and increases with the clock frequency. Using Groundless XNOR gates are implemented. In the proposed Transmission Gate Technique Such unnecessary DFF, the area can be decreased by 62% & substarctor discharging can be prevented. Due to the resistance of circuit, area decreased by 80% and power consumption of switches, impartial losses may be occurred for any DFF and subtractor circuit are 15.4µW and 13.76µW logic operation. respectively, but these are very less as compared to existing techniques. To avoid these minor losses keep clock frequency to be small than the technological limit. There are Keyword: D FF, NMOS, PMOS, VLSI, P-XOR, G-XNOR different types of Transmission Gate logic families. -

High Performance Full Subtractor Using Floating-Gate MOSFET
Microelectronic Engineering 162 (2016) 75–78 Contents lists available at ScienceDirect Microelectronic Engineering journal homepage: www.elsevier.com/locate/mee Accelerated publication High performance full subtractor using floating-gate MOSFET Roshani Gupta, Rockey Gupta, Susheel Sharma Department of Physics and Electronics, University of Jammu, Jammu 180006, India article info abstract Article history: Low power consumption has become one of the primary requirements in the design of digital VLSI circuits in re- Received 18 March 2016 cent years. With scaling down of device dimensions, the supply voltage also needs to be scaled down for reliable Received in revised form 10 May 2016 operation. The speed of conventional digital integrated circuits is degrading on reducing the supply voltage for a Accepted 11 May 2016 given technology. Moreover, the threshold voltage of MOSFET does not scale down proportionally with its di- Available online 13 May 2016 mensions, thus putting a limitation on its suitability for low voltage operation. Therefore, there is a need to ex- Keywords: plore new methodology for the design of digital circuits well suited for low voltage operation and low power Full subtractor consumption. Floating-gate MOS (FGMOS) technology is one of the design techniques with its attractive features FGMOS of reduced circuit complexity and threshold voltage programmability. It can be operated below the conventional TG threshold voltage of MOSFET leading to wider output signal swing at low supply voltage and dissipates less CPL power as compared to CMOS circuits without much compromise on the device performance. This paper presents GDI the design of full subtractor using FGMOS technique whose performance has been compared with full subtractor Power delay product circuits employing CMOS, transmission gates (TG), complementary pass transistor logic (CPL) and gate diffusion input (GDI). -

Design and Implementation of Adder/Subtractor and Multiplication Units for Floating-Point Arithmetic
International Journal of Electronics Engineering, 2(1), 2010, pp. 197-203 Design and Implementation of Adder/Subtractor and Multiplication Units for Floating-Point Arithmetic Dhiraj Sangwan1 & Mahesh K. Yadav2 1MITS University, Laxmangarh, Rajasthan, India 2BRCM College of Engg. & Tech., Bahal, M D University, Rohtak, Haryana, India Abstract: Computers were originally built as fast, reliable and accurate computing machines. It does not matter how large computers get, one of their main tasks will be to always perform computation. Most of these computations need real numbers as an essential category in any real world calculations. Real numbers are not finite; therefore no finite, representation method is capable of representing all real numbers, even within a small range. Thus, most real values will have to be represented in an approximate manner. The scope of this paper includes study and implementation of Adder/Subtractor and multiplication functional units using HDL for computing arithmetic operations and functions suited for hardware implementation. The algorithms are coded in VHDL and validated through extensive simulation. These are structured so that they provide the required performance i.e. speed and gate count. This VHDL code is then synthesized by Synopsys tool to generate the gate level net list that can be implemented on the FPGA using Xilinx FPGA Compiler. Keywords: Algorithm, ALU, Adder/Subtractor, Arithmetic Computation, Floating Point, IEEE 754 Standard, Multiplication, RTL, Significand, Simulation, Synthesis, VHDL. 1. INTRODUCTION normalized floating-point numbers as if they were The Arithmetic logic unit or ALU is the brain of the computer, integers)[9]. the device that performs the arithmetic operations like addition and subtraction or logical operations like AND and 1.2. -

Design of Fault Tolerant Full Subtractor
IJRECE VOL. 6 ISSUE 2 APR.-JUNE 2018 ISSN: 2393-9028 (PRINT) | ISSN: 2348-2281 (ONLINE) Design of Fault Tolerant Full Subtractor Rita Mahajan1, Sharu Bansal2, Deepak Bagai3 Department of Electronics and Communication Engineering Punjab Engineering College (Deemed to be University), Chandigarh, India. [email protected],[email protected],[email protected] Abstract- Now days, the complexity of integrated circuits is extra circuit like generating 2's complement of a number increasing while reliability of the components is decreasing which is to be subtracted. The proposed design is an due to small gates and transistor. One of the impacts of independent subtractor so that addition and subtraction can be technology scaling is more sensitivity to transient and carried out parallel which improves the performance of permanent faults. It is very difficult to detect these faults system. So, the design of faster and reliable subtractor is of offline. The fault tolerant subtractor can detect the faults and great importance in such systems. There are many approaches tolerate the detected faults. There are many fault tolerant full to achieve the fault tolerance in full subtractor. The subtractor which can detect these faults online. So, an efficient researchers have introduced the concept of redundancy to fault tolerant full subtractor is proposed in this paper which detect the fault in full subtractor. But in order to detect and can detect the faults with their exact location and also tolerate tolerate the faults there is need of an efficient fault tolerant full the faults. The proposed subtractor can detect the faults in subtractor. single and multi net. -

8-Bit Adder and Subtractor with Domain Label Based on DNA Strand Displacement
Article 8-Bit Adder and Subtractor with Domain Label Based on DNA Strand Displacement Weixuan Han 1,2 and Changjun Zhou 1,3,* 1 College of Mathematics and Computer Science, Zhejiang Normal University, Jinhua 321004, China; [email protected] 2 College of Nuclear Science and Engineering, Sanmen Institute of technicians, Sanmen 317100, China 3 Key Laboratory of Advanced Design and Intelligent Computing (Dalian University) Ministry of Education, Dalian 116622, China * Correspondence: [email protected] Academic Editor: Xiangxiang Zeng Received: 16 October 2018; Accepted: 13 November 2018; Published: 15 November 2018 Abstract: DNA strand displacement, which plays a fundamental role in DNA computing, has been widely applied to many biological computing problems, including biological logic circuits. However, there are many biological cascade logic circuits with domain labels based on DNA strand displacement that have not yet been designed. Thus, in this paper, cascade 8-bit adder/subtractor with a domain label is designed based on DNA strand displacement; domain t and domain f represent signal 1 and signal 0, respectively, instead of domain t and domain f are applied to representing signal 1 and signal 0 respectively instead of high concentration and low concentration high concentration and low concentration. Basic logic gates, an amplification gate, a fan-out gate and a reporter gate are correspondingly reconstructed as domain label gates. The simulation results of Visual DSD show the feasibility and accuracy of the logic calculation model of the adder/subtractor designed in this paper. It is a useful exploration that may expand the application of the molecular logic circuit. Keywords: DNA strand displacement; cascade; 8-bit adder/subtractor; domain label 1. -

VHDL: Dataflow
Laboratorio de Tecnologías de Información ArithmeticArithmetic andand LogicLogic UnitUnit ArquitecturaArquitectura dede ComputadorasComputadoras Arturo Díaz Pérez Centro de Investigación y de Estudios Avanzados del IPN Laboratorio de Tecnologías de Información [email protected] Arquitectura de Computadoras ALU3- 1 MIPSMIPS arithmeticarithmetic instructionsinstructions Laboratorio de Tecnologías de Información Instruction Example Meaning Comments add add $1,$2,$3 $1 = $2 + $3 3 operands; exception possible subtract sub $1,$2,$3 $1 = $2 – $3 3 operands; exception possible add immediate addi $1,$2,100 $1 = $2 + 100 + constant; exception possible add unsigned addu $1,$2,$3 $1 = $2 + $3 3 operands; no exceptions subtract unsigned subu $1,$2,$3 $1 = $2 – $3 3 operands; no exceptions add imm. unsign. addiu $1,$2,100 $1 = $2 + 100 + constant; no exceptions multiply mult $2,$3 Hi, Lo = $2 x $3 64-bit signed product multiply unsigned multu$2,$3 Hi, Lo = $2 x $3 64-bit unsigned product divide div $2,$3 Lo = $2 ÷ $3, Lo = quotient, Hi = remainder Hi = $2 mod $3 divide unsigned divu $2,$3 Lo = $2 ÷ $3, Unsigned quotient & remainder Hi = $2 mod $3 Move from Hi mfhi $1 $1 = Hi Used to get copy of Hi Move from Lo mflo $1 $1 = Lo Used to get copy of Lo Arquitectura de Computadoras ALU3- 2 ArithmeticArithmetic--logiclogic unitsunits Laboratorio de Tecnologías de Información ♦ An arithmetic-logic unit, or ALU, performs many different arithmetic and logic operations ■ The ALU is the “heart” of a processor—you could say that everything else in the CPU is there to support the ALU ♦ We will show an arithmetic unit first, by building off ideas from the adder-subtractor circuit ♦ Then we will talk about logic operations a bit, and build a logic unit ♦ Finally, we put these pieces together using multiplexers Arquitectura de Computadoras ALU3- 3 TheThe fourfour--bitbit adderadder Laboratorio de Tecnologías de Información ♦ The basic four-bit adder always computes S = A + B + CI. -

Digital Electonics and Microprocessor Date
ELECTRICAL 2ND YEAR SUBJECT- DIGITAL ELECTONICS AND MICROPROCESSOR DATE -01-05-2020 TO 03-05-2020 TIME 9:40-10:30 Arithmetic Circuits Half adder and Full adder circuit, design and implementation, Half and Full subtractor circuit, design and implementation, 4 bit adder/subtractor, Adder and Subtractor IC TOPIC NAME-Half and Full subtractor circuit, As their name implies, a Binary Subtractor is a decision making circuit that subtracts two binary numbers from each other, for example, X – Y to find the resulting difference between the two numbers. Unlike the Binary Adder which produces a SUM and a CARRY bit when two binary numbers are added together, the binary subtractor produces a DIFFERENCE, D by using a BORROW bit, B from the previous column. Then obviously, the operation of subtraction is the opposite to that of addition. We learnt from our maths lessons at school that the minus sign, “–” is used for a subtraction calculation, and when one number is subtracted from another, a borrow is required if the subtrahend is greater than the minuend. Consider the simple subtraction of the two denary (base 10) numbers below. 123 X We can not directly subtract 8 from 3 in the first column as 8 is greater than 3, so we have to borrow a 10, the base number, from the next column and add it to the minuend to produce 13 minus 8. This “borrowed” 10 is then return back to the subtrahend of the next column once the difference is found. Simple school math’s, borrow a 10 if needed, find the difference and return the borrow. -
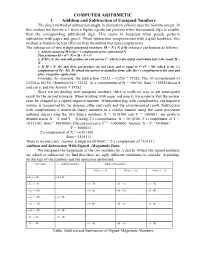
COMPUTER ARITHMETIC 1. Addition and Subtraction of Unsigned Numbers the Direct Method of Subtraction Taught in Elementary Schools Uses the Borrowconcept
COMPUTER ARITHMETIC 1. Addition and Subtraction of Unsigned Numbers The direct method of subtraction taught in elementary schools uses the borrowconcept. In this method we borrow a 1 from a higher significant position when theminuend digit is smaller than the corresponding subtrahend digit. This seems to beeasiest when people perform subtraction with paper and pencil. When subtraction isimplemented with digital hardware, this method is found to be less efficient than themethod that uses complements. The subtraction of two n digit unsigned numbers M – N ( N ≠ 0) in base r can bedone as follows: 1. Add the minuend M to the r’s complement of the subtrahend N. This performs M + (rn– N) = M – N + rn. 2. If M ≥ N, the sum will produce an end carries rn, which is discarded, and whatis left is the result M – N. 3. If M < N, the sum does not produce an end carry and is equal to rn–(N – M), which is the r’s complement of (N – M). To obtain the answer in afamiliar form, take the r’s complement of the sum and place a negative signin front. Consider, for example, the subtraction 72532 – 13250 = 59282. The 10’scomplement of 13250 is 86750. Therefore:M = 72532. 10’s complement of N = +86750. Sum = 159282Discard end carry, and the Answer = 59282 Since we are dealing with unsigned numbers, there is really no way to get anunsigned result for the second example. When working with paper and pencil, werecognize that the answer must be changed to a signed negative number. Whensubtracting with complements, the negative answer is recognized by the absence ofthe end carry and the complemented result. -

Multi‐Bit Adder/Subtractor with Overflow
L07: Circuit Building Blocks I CSE369, Winter 2017 Intro to Digital Design Circuit Building Blocks I Instructor: Justin Hsia L07: Circuit Building Blocks I CSE369, Winter 2017 Practice: String Recognizer FSM Recognize the string 101 with the following behavior . Input: 1 0 0 1 0 1 0 1 1 0 0 1 0 . Output: 0 0 0 0 0 1 0 1 0 0 0 0 0 State diagram to implementation: 2 L07: Circuit Building Blocks I CSE369, Winter 2017 Administrivia Lab 7 – Useful Components . Modifying Lab 6 game to implement common circuit elements • Counter, Shift Registers covered later in lecture . Build a tunable computer opponent . Bonus points for smaller resource usage Quiz 2 is next week in lecture . First 25 minutes, worth 11% of your course grade . On Lectures 4‐6: Sequential Logic, Timing, FSMs, and Verilog . Au16 Quiz 2 (+ solutions) on website: Files Quizzes 3 L07: Circuit Building Blocks I CSE369, Winter 2017 Motivating Example Problem: Implement a simple pocket calculator Need: . Display: Seven segment displays . Inputs: Switches . Math: Arithmetic & Logic Unit (ALU) 4 L07: Circuit Building Blocks I CSE369, Winter 2017 Data Multiplexor Multiplexor (“MUX”) is a selector . Direct one of many ( = s) ‐bit wide inputs onto output . Called a ‐bit, ‐to‐1 MUX Example: ‐bit 2‐to‐1 MUX . Input S ( bits wide) selects between two inputs of bits each This input is passed to output if selector bits inputs match shown value 5 L07: Circuit Building Blocks I CSE369, Winter 2017 Review: Implementing a 1‐bit 2‐to‐1 MUX Schematic: Boolean Algebra: sabc Truth Table: 0 0 00 0 0 10 Circuit Diagram: 0 1 01 0 1 11 100 0 101 1 110 0 111 1 6 L07: Circuit Building Blocks I CSE369, Winter 2017 1‐bit 4‐to‐1 MUX Schematic: Truth Table: How many rows? 26 Boolean Expression: e = s1’s0’a + s1’s0b + s1s0’c + s1s0d 7 L07: Circuit Building Blocks I CSE369, Winter 2017 1‐bit 4‐to‐1 MUX Can we leverage what we’ve previously built? .