DOCSLIB.ORG

The Generalized Distributive Law Srinivas M

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Generalized Distributive Law Srinivas M IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 46, NO. 2, MARCH 2000 325 The Generalized Distributive Law Srinivas M. Aji and Robert J. McEliece, Fellow, IEEE Abstract—In this semitutorial paper we discuss a general (We summarize (1.1) by saying that is obtained by message passing algorithm, which we call the generalized dis- “marginalizing out” the variables and from the function tributive law (GDL). The GDL is a synthesis of the work of many . Similarly, is obtained by marginalizing authors in the information theory, digital communications, signal processing, statistics, and artificial intelligence communities. It out , , and from the same function.) How many arithmetic includes as special cases the Baum–Welch algorithm, the fast operations (additions and multiplications) are required for this Fourier transform (FFT) on any finite Abelian group, the Gal- task? If we proceed in the obvious way, we notice that for each lager–Tanner–Wiberg decoding algorithm, Viterbi’s algorithm, of the values of there are terms in the sum defining the BCJR algorithm, Pearl’s “belief propagation” algorithm, the , each term requiring one addition and one multiplica- Shafer–Shenoy probability propagation algorithm, and the turbo decoding algorithm. Although this algorithm is guaranteed to give tion, so that the total number of arithmetic operations required exact answers only in certain cases (the “junction tree” condition), for the computation of is . Similarly, computing unfortunately not including the cases of GTW with cycles or requires operations, so computing both and turbo decoding, there is much experimental evidence, and a few using the direct method requires operations. theorems, suggesting that it often works approximately even when On the other hand, because of the distributive law, the sum in it is not supposed to. (1.1) factors Index Terms—Belief propagation, distributive law, graphical models, junction trees, turbo codes. (1.3) I. INTRODUCTION HE humble distributive law, in its simplest form, states that Using this fact, we can simplify the computation of . T . The left side of this equation involves First we compute tables of the functions and three arithmetic operations (one addition and two multiplica- defined by tions), whereas the right side needs only two. Thus the distribu- tive law gives us a “fast algorithm” for computing . The object of this paper is to demonstrate that the distributive law can be vastly generalized, and that this generalization leads to (1.4) a large family of fast algorithms, including Viterbi’s algorithm and the fast Fourier transform (FFT).To give a better idea of the potential power of the distributive law and to introduce the view- which requires a total of additions. Then we compute point we shall take in this paper, we offer the following example. the values of using the formula (cf. (1.3)) Example 1.1: Let and be given (1.5) real-valued functions, where , , , and are variables taking values in a finite set with elements. Suppose we are given which requires multiplications. Thus by exploiting the dis- the task of computing tables of the values of and , tributive law, we can reduce the total number of operations re- defined as follows: quired to compute from to . Similarly, the distributive law tells us that (1.2) can be written as (1.1) (1.2) (1.6) Manuscript received July 8, 1998; revised September 23, 1999. This work was supported by NSF under Grant NCR-9505975, AFOSR under Grant 5F49620-97-1-0313, and a Grant from Qualcomm. A portion of McEliece’s where is as defined in (1.4). Thus if we precompute a contribution was performed at the Sony Corporation in Tokyo, Japan, while he table of the values of ( operations), and then use (1.6) was a holder of a Sony Sabbatical Chair. Preliminary versions of this paper ( further operations), we only need operations (as were presented at the IEEE International Symposium on Information Theory, Ulm, Germany, June 1997, and at ISCTA 1997, Ambleside U.K., July 1997. compared to for the direct method) to compute the values The authors are with the Department of Electrical Engineering, California of . Institute of Technology, Pasadena, CA 91125 USA (e-mail: {mas; rjm}@sys- Finally, we observe that to compute both and tems.caltech.edu). Communicated by F. R. Kschischang, Associate Editor for Coding Theory. using the simplifications afforded by (1.3) and (1.6), we only Publisher Item Identifier S 0018-9448(00)01679-5. need to compute once, which means that we can compute 0018–9448/00$10.00 © 2000 IEEE 326 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 46, NO. 2, MARCH 2000 the values of and with a total of only some recent theoretical work on GDL-like algorithms on graphs operations, as compared to for the direct method. with a single cycle. Although this paper is semitutorial, it contains a number of The simplification in Example 1.1 was easy to accomplish, things which have not appeared previously. Beside the gener- and the gains were relatively modest. In more complicated ality of our exposition, these include: cases, it can be much harder to see the best way to reorganize the calculations, but the computational savings can be dramatic. • A de-emphasis of a priori graphical models, and an em- It is the object of this paper to show that problems of the type phasis on algorithms to construct graphical models to fit described in Example 1.1 have a wide range of applicability, the given problem. and to describe a general procedure, which we called the gen- • A number of nonprobabilistic applications, including the eralized distributive law (GDL), for solving them efficiently. FFT. Roughly speaking, the GDL accomplishes its goal by passing • A careful discussion of message scheduling, and a proof messages in a communications network whose underlying of the correctness of a large class of possible schedules. graph is a tree. • A precise measure of the computational complexity of the Important special cases of the GDL have appeared many GDL. times previously. In this paper, for example, we will demon- Finally, we note that while this paper was being written, strate that the GDL includes as special cases the fast Hadamard Kschischang, Frey, and Loeliger [41] were simultaneously transform, Viterbi’s algorithm, the BCJR algorithm, the and independently working out a similar synthesis. And while Gallager–Tanner–Wiberg decoding algorithm (when the under- the final forms of the two papers have turned out to be quite lying graph is cycle-free), and certain “probability propagation” different, anyone interested in the results of this paper should algorithms known in the artificial intelligence community. have a look at the alternative formulation in [41]. With a little more work, we could have added the FFT on any finite Abelian group, the Baum–Welch “forward-backward” II. THE MPF PROBLEM algorithm, and discrete-state Kalman filtering. Although this The GDL can greatly reduce the number of additions and paper contains relatively little that is essentially new (for multiplications required in a certain class of computational example, the 1990 paper of Shafer and Shenoy [33] describes problems. It turns out that much of the power of the GDL is an algorithm similar to the one we present in Section III), we due to the fact that it applies to situations in which the notions believe it is worthwhile to present a simply stated algorithm of addition and multiplication are themselves generalized. The of such wide applicability, which gives a unified treatment of appropriate framework for this generalization is the commuta- a great many algorithms whose relationship to each other was tive semiring. not fully understood, if sensed at all. Here is an outline of the paper. In Section II, we will state a Definition: A commutative semiring is a set , together with general computational problem we call the MPF (“marginalize two binary operations called “ ” and “ ”, which satisfy the fol- a product function”) problem, and show by example that lowing three axioms: a number of classical problems are instances of it. These S1. The operation “ ” is associative and commutative, and problems include computing the discrete Hadamard transform, there is an additive identity element called “ ” such that maximum-likelihood decoding of a linear code over a memo- for all . (This axiom makes ryless channel, probabilistic inference in Bayesian networks, a commutative monoid.) a “probabilistic state machine” problem, and matrix chain S2. The operation “ ” is also associative and commutative, multiplication. In Section III, we shall give an exact algorithm and there is a multiplicative identity element called “ ” for solving the MPF problem (the GDL) which often gives such that for all . (Thus is also an efficient solution to the MPF problem. In Section IV we a commutative monoid.) will discuss the problem of finding junction trees (the formal S3. The distributive law holds, i.e., name for the GDL’s communication network), and “solve” the example instances of the MPF problem given in Section II, thereby deriving, among other things, the fast Hadamard for all triples from . transform and Viterbi’s algorithm. In Section V we will discuss the computational complexity of the GDL. (A proof of the The difference between a semiring and a ring is that in a correctness of the GDL is given in the Appendix.) semiring, additive inverses need not exist, i.e., is only In Section VI, we give a brief history of the GDL. Finally, required to be a monoid, not a group. Thus every commutative in Section VII, we speculate on the possible existence of an ring is automatically a commutative semiring. For example, the efficient class of approximate, iterative, algorithms for solving set of real or complex numbers, with ordinary addition and mul- the MPF problem, obtained by allowing the communication net- tiplication, forms a commutative semiring.
Load more

Recommended publications
  • Estimation of Viterbi Path in Bayesian Hidden Markov Models
    Estimation of Viterbi path in Bayesian hidden Markov models Jüri Lember1,∗ Dario Gasbarra2, Alexey Koloydenko3 and Kristi Kuljus1 May 14, 2019 1University of Tartu, Estonia; 2University of Helsinki, Finland; 3Royal Holloway, University of London, UK Abstract The article studies different methods for estimating the Viterbi path in the Bayesian framework. The Viterbi path is an estimate of the underlying state path in hidden Markov models (HMMs), which has a maximum joint posterior probability. Hence it is also called the maximum a posteriori (MAP) path. For an HMM with given parameters, the Viterbi path can be easily found with the Viterbi algorithm. In the Bayesian framework the Viterbi algorithm is not applicable and several iterative methods can be used instead. We introduce a new EM-type algorithm for finding the MAP path and compare it with various other methods for finding the MAP path, including the variational Bayes approach and MCMC methods. Examples with simulated data are used to compare the performance of the methods. The main focus is on non-stochastic iterative methods and our results show that the best of those methods work as well or better than the best MCMC methods. Our results demonstrate that when the primary goal is segmentation, then it is more reasonable to perform segmentation directly by considering the transition and emission parameters as nuisance parameters. Keywords: HMM, Bayes inference, MAP path, Viterbi algorithm, segmentation, EM, variational Bayes, simulated annealing 1 Introduction and preliminaries arXiv:1802.01630v2 [stat.CO] 11 May 2019 Hidden Markov models (HMMs) are widely used in application areas including speech recognition, com- putational linguistics, computational molecular biology, and many more.
    [Show full text]
  • Sequence Models
    Sequence Models Noah Smith Computer Science & Engineering University of Washington [email protected] Lecture Outline 1. Markov models 2. Hidden Markov models 3. Viterbi algorithm 4. Other inference algorithms for HMMs 5. Learning algorithms for HMMs Shameless Self-Promotion • Linguistic Structure Prediction (2011) • Links material in this lecture to many related ideas, including some in other LxMLS lectures. • Available in electronic and print form. MARKOV MODELS One View of Text • Sequence of symbols (bytes, letters, characters, morphemes, words, …) – Let Σ denote the set of symbols. • Lots of possible sequences. (Σ* is infinitely large.) • Probability distributions over Σ*? Pop QuiZ • Am I wearing a generative or discriminative hat right now? Pop QuiZ • Generative models tell a • Discriminative models mythical story to focus on tasks (like explain the data. sorting examples). Trivial Distributions over Σ* • Give probability 0 to sequences with length greater than B; uniform over the rest. • Use data: with N examples, give probability N-1 to each observed sequence, 0 to the rest. • What if we want every sequence to get some probability? – Need a probabilistic model family and algorithms for constructing the model from data. A History-Based Model n+1 p(start,w1,w2,...,wn, stop) = γ(wi w1,w2,...,wi 1) | − i=1 • Generate each word from left to right, conditioned on what came before it. Die / Dice one die two dice start one die per history: … … … start I one die per history: … … … history = start start I want one die per history: … … history = start I … start I want a one die per history: … … … history = start I want start I want a flight one die per history: … … … history = start I want a start I want a flight to one die per history: … … … history = start I want a flight start I want a flight to Lisbon one die per history: … … … history = start I want a flight to start I want a flight to Lisbon .
    [Show full text]
  • Viterbi Extraction Tutorial with Hidden Markov Toolkit
    Viterbi Extraction tutorial with Hidden Markov Toolkit Zulkarnaen Hatala 1, Victor Puturuhu 2 Electrical Engineering Department Politeknik Negeri Ambon Ambon, Indonesia [email protected] [email protected] Abstract —An algorithm used to extract HMM parameters condition probabilities. The distribution of observation only is revisited. Most parts of the extraction process are taken from depends on the current state of Markov chain. In some implemented Hidden Markov Toolkit (HTK) program under application not all states of Markov chain emit observations. name HInit. The algorithm itself shows a few variations Set of states that emit an observation is called emitting states, compared to another domain of implementations. The HMM while non emitting states could be an entry or start state, model is introduced briefly based on the theory of Discrete absorption or exiting state and intermediate or delaying state. Time Markov Chain. We schematically outline the Viterbi The entry state is the Markov chain state with initial method implemented in HTK. Iterative definition of the probability 1. method which is ready to be implemented in computer programs is reviewed. We also illustrate the method One application of Hidden Markov Model is in speech calculation precisely using manual calculation and extensive recognition. The observations of HMM are used to model graphical illustration. The distribution of observation sequence of speech feature vectors like Mel Frequency probability used is simply independent Gaussians r.v.s. The Cepstral Coefficients (MFCC) [4]. MFCC is assumed to be purpose of the content is not to justify the performance or generated by emitting hidden states of the underlying accuracy of the method applied in a specific area.
    [Show full text]
  • Markov Chains and Hidden Markov Models
    COMP 182 Algorithmic Thinking Luay Nakhleh Markov Chains and Computer Science Hidden Markov Models Rice University ❖ What is p(01110000)? ❖ Assume: ❖ 8 independent Bernoulli trials with success probability of α? ❖ Answer: ❖ (1-α)5α3 ❖ However, what if the assumption of independence doesn’t hold? ❖ That is, what if the outcome in a Bernoulli trial depends on the outcomes of the trials the preceded it? Markov Chains ❖ Given a sequence of observations X1,X2,…,XT ❖ The basic idea behind a Markov chain (or, Markov model) is to assume that Xt captures all the relevant information for predicting the future. ❖ In this case: T p(X1X2 ...XT )=p(X1)p(X2 X1)p(X3 X2) p(XT XT 1)=p(X1) p(Xt Xt 1) | | ··· | − | − t=2 Y Markov Chains ❖ When Xt is discrete, so Xt∈{1,…,K}, the conditional distribution p(Xt|Xt-1) can be written as a K×K matrix, known as the transition matrix A, where Aij=p(Xt=j|Xt-1=i) is the probability of going from state i to state j. ❖ Each row of the matrix sums to one, so this is called a stochastic matrix. 590 Chapter 17. Markov and hidden Markov models Markov Chains 1 α 1 β − α − A11 A22 A33 1 2 A12 A23 1 2 3 β ❖ A finite-state Markov chain is equivalent(a) (b) Figure 17.1 State transition diagrams for some simple Markov chains. Left: a 2-state chain. Right: a to a stochastic automaton3-state left-to-right. chain. ❖ One way to represent aAstationary,finite-stateMarkovchainisequivalenttoa Markov chain is stochastic automaton.Itiscommon 590 to visualizeChapter such 17.
    [Show full text]
  • N-Best Hypotheses
    FIANAL PROJECT REPORT NAME: Shuan wang STUDENT #: 21224043 N-best Hypotheses [INDEX] 1. Introduction 1.1 Project Goal 1.2 Sources of Interest 1.3 Current Work 2. Implemented Three Algorithms 2.1 General Viterbi Algorithm 2.1.1 Basic Ideas 2.1.2 Implementation 2.2 N-Best List in HMM 2.2.1 Basic Ideas 2.2.2 Implementation 2.3 BMMF (Best Max-Marginal First) 2.3.1 Basic Ideas 2.3.2 Implementation 3. Some Experiment Results 4. Future Work 5. References 1 of 8 FIANAL PROJECT REPORT NAME: Shuan wang STUDENT #: 21224043 1. Introduction It’s very useful to find the top N most probable figures of hidden variable sequence. There are some important methods in recent years to find such kind of N figures: (1) General Viterbi Algorithm (2) MFP (Max-Flow Propagation), by Nilson and Lauritzen in 1998 (3) N-Best List in HMM, by Nilson and Goldberger in 2001 (4) BMMF (Best Max-Marginal First), by Chen Yanover and Yair Weiss in 2003 In this project my task is to realize part of these algorithms and test the results. 1.1 Project Goal The project goal is to totally understand the basic algorithm ideas and try to realize the most recent three of them (MFP, N-Best List in HMM, BMMF) and test them. 1.2 Sources of Interest Many applications, such as protein folding, vocabulary speech recognition and image analysis, want to find not just the best configuration of the hidden variables (state sequence), but rather the top N. Normally the recognizers in these applications are based on a relatively simple model.
    [Show full text]
  • Graphical Models
    Graphical Models Unit 11 Machine Learning University of Vienna Graphical Models Bayesian Networks (directed graph) The Variable Elimination Algorithm Approximate Inference (The Gibbs Sampler ) Markov networks (undirected graph) Markov Random fields (MRF) Hidden markov models (HMMs) The Viterbi Algorithm Kalman Filter Simple graphical model 1 The graphs are the sets of nodes, together with the links between them, which can be either directed or not. If two nodes are not linked, than those two variables are independent. The arrows denote causal relationships between nodes that represent features. The probability of A and B is the same as the probability of A times the probability of B conditioned on A: P(a; b) = P(bja)P(a) Simple graphical model 2 The nodes are separated into: • observed nodes: where we can see their values directly • hidden or latent nodes: whose values we hope to infer, and which may not have clear meanings in all cases. C is conditionally independent of B, given A Example: Exam Panic Directed acyclic graphs (DAG) paired with the conditional probability tables are called Bayesian networks. B - denotes a node stating whether the exam was boring R - whether or not you revised A - whether or not you attended lectures P - whether or not you will panic before the exam Example: Exam Panic R P(r) P(:r) P(b) P(:b) T 0.3 0.7 0.5 0.5 F 0.8 0.2 RA P(p) P(:p) A P(a) P(:a) TT 0 1 T 0.1 0.9 TF 0.8 0.2 F 0.5 0.5 FT 0.6 0.4 FF 1 0 P The probability of panicking: P(p) = b;r;a P(b; r; a; p) = P b;r;a P(b) × P(rjb) × P(ajb) × P(pjr; a) Example: Exam Panic Suppose you know that the course was boring, and want to work out how likely it is that you will panic before exam.
    [Show full text]
  • Hidden Markov Models in Bioinformatics
    Current Bioinformatics, 2007, 2, 49-61 49 Hidden Markov Models in Bioinformatics Valeria De Fonzo1, Filippo Aluffi-Pentini2 and Valerio Parisi*,3 1EuroBioPark, Università di Roma “Tor Vergata”, Via della Ricerca Scientifica 1, 00133 Roma, Italy 2Dipartimento Metodi e Modelli Matematici, Università di Roma “La Sapienza”, Via A. Scarpa 16, 00161 Roma, Italy 3Dipartimento di Medicina Sperimentale e Patologia, Università di Roma “La Sapienza”, Viale Regina Elena 324, 00161 Roma, Italy Abstract: Hidden Markov Models (HMMs) became recently important and popular among bioinformatics researchers, and many software tools are based on them. In this survey, we first consider in some detail the mathematical foundations of HMMs, we describe the most important algorithms, and provide useful comparisons, pointing out advantages and drawbacks. We then consider the major bioinformatics applications, such as alignment, labeling, and profiling of sequences, protein structure prediction, and pattern recognition. We finally provide a critical appraisal of the use and perspectives of HMMs in bioinformatics. Keywords: Hidden markov model, HMM, dynamical programming, labeling, sequence profiling, structure prediction. INTRODUCTION this case, the time evolution of the internal states can be induced only through the sequence of the observed output A Markov process is a particular case of stochastic states. process, where the state at every time belongs to a finite set, the evolution occurs in a discrete time and the probability If the number of internal states is N, the transition distribution of a state at a given time is explicitly dependent probability law is described by a matrix with N times N only on the last states and not on all the others.
    [Show full text]
  • Hidden Markov Model: Tutorial
    Hidden Markov Model: Tutorial Benyamin Ghojogh [email protected] Department of Electrical and Computer Engineering, Machine Learning Laboratory, University of Waterloo, Waterloo, ON, Canada Fakhri Karray [email protected] Department of Electrical and Computer Engineering, Centre for Pattern Analysis and Machine Intelligence, University of Waterloo, Waterloo, ON, Canada Mark Crowley [email protected] Department of Electrical and Computer Engineering, Machine Learning Laboratory, University of Waterloo, Waterloo, ON, Canada Abstract emitted observation symbols (Rabiner, 1989). HMM mod- This is a tutorial paper for Hidden Markov Model els the the probability density of a sequence of observed (HMM). First, we briefly review the background symbols (Roweis, 2003). on Expectation Maximization (EM), Lagrange This paper is a technical tutorial for evaluation, estima- multiplier, factor graph, the sum-product algo- tion, and training in HMM. We also explain some applica- rithm, the max-product algorithm, and belief tions for HMM. There exist many different applications for propagation by the forward-backward procedure. HMM. One of the most famous applications is in speech Then, we introduce probabilistic graphical mod- recognition (Rabiner, 1989; Gales et al., 2008) where an els including Markov random field and Bayesian HMM is trained for every word in the speech (Rabiner & network. Markov property and Discrete Time Juang, 1986). Another application of HMM is in action Markov Chain (DTMC) are also introduced. We, recognition (Yamato et al., 1992) because an action can then, explain likelihood estimation and EM in be seen as a sequence or times series of poses (Ghojogh HMM in technical details. We explain evalua- et al., 2017; Mokari et al., 2018).
    [Show full text]
  • Lecture 6A: Introduction to Hidden Markov Models
    Lecture 6a: Introduction to Hidden Markov Models Introduction to Computational Biology Instructor: Teresa Przytycka, PhD Igor Rogozin PhD First order Markov model (informal) α A G β β β β β,α -probability of given mutation in a unit of time C T α transversion transition A random walk in this graph will generates a path; say AATTCA…. For each such path we can compute the probability of the path In this graph every path is possible (with different probability) but in general this does need to be true. First order Markov model (formal) Markov model is represented by a graph with set of vertices corresponding to the set of states Q and probability of going from state i to state j in a random walk described by matrix a: a – n x n transition probability matrix a(i,j)= P[q t+1=j|q t=i] where q t denotes state at time t Thus Markov model M is described by Q and a M = (Q, a) Example 1/4 Transition probabilities for general DNA seq. Set of states Q: {Begin, End, A,T,C,G} Transition probability matrix a: a Probability of a sequence of states S=q0,…,qm in model M Assume a random walk that starts from state q0 and goes for m steps. What is the probability that S= q0,…,qm is the sequence of states visited? P(S|M) = a(q0,q1) a(q1 , q2) a(q2 , q3) … a(qm-1 , qm) P(S|M) = probability of visiting sequence of states S assuming Markov model M defined by a: n x n transition probability matrix a(i,j) = Pr[q t+1=j|q t=i] Example 1/4 Transition probabilities for general DNA seq.
    [Show full text]
  • Hidden Markov Models + Conditional Random Fields
    10-715 Advanced Intro. to Machine Learning Machine Learning Department School of Computer Science Carnegie Mellon University Hidden Markov Models + Conditional Random Fields Matt Gormley Guest Lecture 2 Oct. 31, 2018 1 1. Data 2. Model (n) N 1 = x n=1 p(x ✓)= (x ) D { } | Z(✓) C C n v p d n Sample 1: C time flies like an arrow Y2C T1 T2 T3 T4 T5 Sample n n v d n 2: W W W W W time flies like an arrow 1 2 3 4 5 Sample n v p n n 3: flies fly with their wings 3. Objective N Sample p n n v v (n) 4: `(✓; )= log p(x ✓) with time you will see D | n=1 X 5. Inference 4. Learning 1. Marginal Inference p(x )= p(x0 ✓) ✓⇤ = argmax `(✓; ) C | x :x =x D 0 C0 C ✓ 2. Partition Function X Z(✓)= C (xC ) x C 3. MAP Inference X Y2C xˆ = argmax p(x ✓) x | 2 HIDDEN MARKOV MODEL (HMM) 3 Dataset for Supervised Part-of-Speech (POS) Tagging Data: = x(n), y(n) N D { }n=1 n v p d n y(1) Sample 1: time flies like an arrow x(1) n n v d n y(2) Sample 2: time flies like an arrow x(2) (3) n v p n n y Sample 3: (3) flies fly with their wings x (4) p n n v v y Sample 4: (4) with time you will see x 4 Naïve Bayes for Time Series Data We could treat each word-tag pair (i.e.
    [Show full text]
  • 4A. Inference in Graphical Models Inference on a Chain (Rep.)
    Computer Vision Group Prof. Daniel Cremers 4a. Inference in Graphical Models Inference on a Chain (Rep.) • The first values of µα and µβ are: • The partition function can be computed at any node: • Overall, we have O(NK2) operations to compute the marginal Machine Learning for Dr. Rudolph Triebel Computer Vision 2 Computer Vision Group More General Graphs The message-passing algorithm can be extended to more general graphs: Directed Undirected Polytree Tree Tree It is then known as the sum-product algorithm. A special case of this is belief propagation. Machine Learning for Dr. Rudolph Triebel Computer Vision 3 Computer Vision Group More General Graphs The message-passing algorithm can be extended to more general graphs: Undirected Tree An undirected tree is defined as a graph that has exactly one path between any two nodes Machine Learning for Dr. Rudolph Triebel Computer Vision 4 Computer Vision Group More General Graphs The message-passing algorithm can be extended to more general graphs: Directed A directed tree has Tree Conversion from only one node a directed to an without parents and undirected tree is all other nodes no problem, have exactly one because no links parent are inserted The same is true for the conversion back to a directed tree Machine Learning for Dr. Rudolph Triebel Computer Vision 5 Computer Vision Group More General Graphs The message-passing algorithm can be extended to more general graphs: Polytree Polytrees can contain nodes with several parents, therefore moralization can remove independence relations Machine Learning for Dr. Rudolph Triebel Computer Vision 6 Computer Vision Group Factor Graphs • The Sum-product algorithm can be used to do inference on undirected and directed graphs.
    [Show full text]
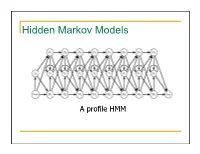
  • Hidden Markov Models
    Hidden Markov Models A profile HMM What is a HMM? • It’s a model. It condenses information. • Models 1D discrete data. • Directed graph. • Nodes emit discrete data • Edges transition between nodes. • What’s hidden about it? • Node identity. • Who is Markov? 2 Markov processes time sequence Markov process is any process where the next item in the list depends on the current item. The dimension can be time, sequence position, etc Modeling protein secondary structure using Markov chains “states” connected by “transitions” H E H=helix E=extended (strand) L L=loop Setting the parameters of a Markov model from data. Secondary structure data LLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLEEEEELLLLEEEEELLLLLLLLLLLEEEEEEEEELLLLLEEEEEEEEELL LLLLLLEEEEEELLLLLEEEEEELLLLLLLLLLLLLLLEEEEEELLLLLEEEEELLLLLLLLLLEEEELLLLEEEELLLLEEE EEEEELLLLLLEEEEEEEEELLLLLLEELLLLLLLLLLLLLLLLLLLLLLLLEEEEELLLEEEEEELLLLLLLLLLEEEEEEL LLLLEEELLLLLLLLLLLLLEEEEEEEEELLLEEEEEELLLLLLLLLLLLLLLLLLLHHHHHHHHHHHHHLLLLLLLEEL HHHHHHHHHHLLLLLLHHHHHHHHHHHLLLLLLLELHHHHHHHHHHHHLLLLLHHHHHHHHHHHHHLLLLLEEEL HHHHHHHHHHLLLLLLHHHHHHHHHHEELLLLLLHHHHHHHHHHHLLLLLLLHHHHHHHHHHHHHHHHHHHHH HHHHHHLLLLLLHHHHHHHHHHHHHHHHHHLLLHHHHHHHHHHHHHHLLLLEEEELLLLLLLLLLLLLLLLEEEEL LLLHHHHHHHHHHHHHHHLLLLLLLLEELLLLLHHHHHHHHHHHHHHLLLLLLEEEEELLLLLLLLLLHHHHHHHH HHHHHHHHHHHHHHHLLLLLHHHHHHHHHLLLLHHHHHHHLLHHHHHHHHHHHHHHHHHHHH Count the pairs to get the transition probability. E P(L|E) L P(L|E) = P(EL)/P(E) = counts(EL)/counts(E) counts(E) = counts(EE) + counts(EL) + counts(EH) Therefore: P(E|E) + P(L|E) + P(H|E) = 1. A transition matrix P(H|H)
    [Show full text]