Exomoon Habitability Constrained by Illumination and Tidal Heating
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lab 7: Gravity and Jupiter's Moons
Lab 7: Gravity and Jupiter's Moons Image of Galileo Spacecraft Gravity is the force that binds all astronomical structures. Clusters of galaxies are gravitationally bound into the largest structures in the Universe, Galactic Superclusters. The galaxies themselves are held together by gravity, as are all of the star systems within them. Our own Solar System is a collection of bodies gravitationally bound to our star, Sol. Cutting edge science requires the use of Einstein's General Theory of Relativity to explain gravity. But the interactions of the bodies in our Solar System were understood long before Einstein's time. In chapter two of Chaisson McMillan's Astronomy Today, you went over Kepler's Laws. These laws of gravity were made to describe the interactions in our Solar System. P2=a3/M Where 'P' is the orbital period in Earth years, the time for the body to make one full orbit. 'a' is the length of the orbit's semi-major axis, for nearly circular orbits the orbital radius. 'M' is the total mass of the system in units of Solar Masses. Jupiter System Montage picture from NASA ID = PIA01481 Jupiter has over 60 moons at the last count, most of which are asteroids and comets captured from Written by Meagan White and Paul Lewis Page 1 the Asteroid Belt. When Galileo viewed Jupiter through his early telescope, he noticed only four moons: Io, Europa, Ganymede, and Callisto. The Jupiter System can be thought of as a miniature Solar System, with Jupiter in place of the Sun, and the Galilean moons like planets. -
The Geology of the Rocky Bodies Inside Enceladus, Europa, Titan, and Ganymede
49th Lunar and Planetary Science Conference 2018 (LPI Contrib. No. 2083) 2905.pdf THE GEOLOGY OF THE ROCKY BODIES INSIDE ENCELADUS, EUROPA, TITAN, AND GANYMEDE. Paul K. Byrne1, Paul V. Regensburger1, Christian Klimczak2, DelWayne R. Bohnenstiehl1, Steven A. Hauck, II3, Andrew J. Dombard4, and Douglas J. Hemingway5, 1Planetary Research Group, Department of Marine, Earth, and Atmospheric Sciences, North Carolina State University, Raleigh, NC 27695, USA ([email protected]), 2Department of Geology, University of Georgia, Athens, GA 30602, USA, 3Department of Earth, Environmental, and Planetary Sciences, Case Western Reserve University, Cleveland, OH 44106, USA, 4Department of Earth and Environmental Sciences, University of Illinois at Chicago, Chicago, IL 60607, USA, 5Department of Earth & Planetary Science, University of California Berkeley, Berkeley, CA 94720, USA. Introduction: The icy satellites of Jupiter and horizontal stresses, respectively, Pp is pore fluid Saturn have been the subjects of substantial geological pressure (found from (3)), and μ is the coefficient of study. Much of this work has focused on their outer friction [12]. Finally, because equations (4) and (5) shells [e.g., 1–3], because that is the part most readily assess failure in the brittle domain, we also considered amenable to analysis. Yet many of these satellites ductile deformation with the relation n –E/RT feature known or suspected subsurface oceans [e.g., 4– ε̇ = C1σ exp , (6) 6], likely situated atop rocky interiors [e.g., 7], and where ε̇ is strain rate, C1 is a constant, σ is deviatoric several are of considerable astrobiological significance. stress, n is the stress exponent, E is activation energy, R For example, chemical reactions at the rock–water is the universal gas constant, and T is temperature [13]. -

Galileo and the Telescope
Galileo and the Telescope A Discussion of Galileo Galilei and the Beginning of Modern Observational Astronomy ___________________________ Billy Teets, Ph.D. Acting Director and Outreach Astronomer, Vanderbilt University Dyer Observatory Tuesday, October 20, 2020 Image Credit: Giuseppe Bertini General Outline • Telescopes/Galileo’s Telescopes • Observations of the Moon • Observations of Jupiter • Observations of Other Planets • The Milky Way • Sunspots Brief History of the Telescope – Hans Lippershey • Dutch Spectacle Maker • Invention credited to Hans Lippershey (c. 1608 - refracting telescope) • Late 1608 – Dutch gov’t: “ a device by means of which all things at a very great distance can be seen as if they were nearby” • Is said he observed two children playing with lenses • Patent not awarded Image Source: Wikipedia Galileo and the Telescope • Created his own – 3x magnification. • Similar to what was peddled in Europe. • Learned magnification depended on the ratio of lens focal lengths. • Had to learn to grind his own lenses. Image Source: Britannica.com Image Source: Wikipedia Refracting Telescopes Bend Light Refracting Telescopes Chromatic Aberration Chromatic aberration limits ability to distinguish details Dealing with Chromatic Aberration - Stop Down Aperture Galileo used cardboard rings to limit aperture – Results were dimmer views but less chromatic aberration Galileo and the Telescope • Created his own (3x, 8-9x, 20x, etc.) • Noted by many for its military advantages August 1609 Galileo and the Telescope • First observed the -

Water Masers in the Saturnian System
A&A 494, L1–L4 (2009) Astronomy DOI: 10.1051/0004-6361:200811186 & c ESO 2009 Astrophysics Letter to the Editor Water masers in the Saturnian system S. V. Pogrebenko1,L.I.Gurvits1, M. Elitzur2,C.B.Cosmovici3,I.M.Avruch1,4, S. Montebugnoli5 , E. Salerno5, S. Pluchino3,5, G. Maccaferri5, A. Mujunen6, J. Ritakari6, J. Wagner6,G.Molera6, and M. Uunila6 1 Joint Institute for VLBI in Europe, PO Box 2, 7990 AA Dwingeloo, The Netherlands e-mail: [pogrebenko;lgurvits]@jive.nl 2 Department of Physics and Astronomy, University of Kentucky, 600 Rose Street, Lexington, KY 40506-0055, USA e-mail: [email protected] 3 Istituto Nazionale di Astrofisica (INAF) – Istituto di Fisica dello Spazio Interplanetario (IFSI), via del Fosso del Cavaliere, 00133 Rome, Italy e-mail: [email protected] 4 Science & Technology BV, PO 608 2600 AP Delft, The Netherlands e-mail: [email protected] 5 Istituto Nazionale di Astrofisica (INAF) – Istituto di Radioastronomia (IRA) – Stazione Radioastronomica di Medicina, via Fiorentina 3508/B, 40059 Medicina (BO), Italy e-mail: [s.montebugnoli;e.salerno;g.maccaferri]@ira.inaf.it; [email protected] 6 Helsinki University of Technology TKK, Metsähovi Radio Observatory, 02540 Kylmälä, Finland e-mail: [amn;jr;jwagner;gofrito;minttu]@kurp.hut.fi Received 18 October 2008 / Accepted 4 December 2008 ABSTRACT Context. The presence of water has long been seen as a key condition for life in planetary environments. The Cassini spacecraft discovered water vapour in the Saturnian system by detecting absorption of UV emission from a background star. Investigating other possible manifestations of water is essential, one of which, provided physical conditions are suitable, is maser emission. -

The Jovian Planets (Gas Giants) Discoveries
The Jovian Planets (Gas Giants) Discoveries Saturn Jupiter Jupiter and Saturn known to ancient astronomers. Uranus discovered in 1781 by Sir William Herschel (England). Neptune discovered in 1845 by Johann Galle (Germany). Predicted to exist by John Adams and Urbain Leverrier because of irregularities in Uranus' orbit. Almost discovered by Galileo in 1613 Uranus Neptune (roughly to scale) Remember that compared to Terrestrial planets, Jovian planets: Orbital Properties: Distance from Sun Orbital Period are massive (AU) (years) are less dense (0.7 – 1.3 g/cm3) Jupiter 5.2 11.9 are mostly gas (and liquid) Saturn 9.5 29.4 rotate fast (9 - 17 hours rotation periods) Uranus 19.2 84 have rings and many moons Neptune 30.1 164 Known Moons Mass (MEarth) Radius (REarth) Major Missions: Launch Planets visited Jupiter 318 11 63 Voyager 1 1977 Jupiter, Saturn (0.001 MSun) Saturn 95 9.5 50 Voyager 2 1979 Jupiter, Saturn, Uranus, Neptune Uranus 15 4 27 Galileo 1989 Jupiter Neptune 17 3.9 13 Cassini 1997 Jupiter, Saturn Jupiter's Atmosphere Composition: mostly H, some He, traces of other elements (true for all Jovians). Gravity strong enough to retain even light elements. Mostly molecular. Altitude 0 km defined as top of troposphere (cloud layer) Ammonia (NH3) ice gives white colors. Ammonium hydrosulfide Optical – colors dictated Infrared - traces heat in (NH4SH) ice should form by how molecules atmosphere. here, somehow giving red, reflect sunlight yellow, brown colors. Water ice layer not seen due to higher layers. So white colors from cooler, higher clouds, brown and red from warmer, lower clouds. -

A Deeper Look at the Colors of the Saturnian Irregular Satellites Arxiv
A deeper look at the colors of the Saturnian irregular satellites Tommy Grav Harvard-Smithsonian Center for Astrophysics, MS51, 60 Garden St., Cambridge, MA02138 and Instiute for Astronomy, University of Hawaii, 2680 Woodlawn Dr., Honolulu, HI86822 [email protected] James Bauer Jet Propulsion Laboratory, California Institute of Technology 4800 Oak Grove Dr., MS183-501, Pasadena, CA91109 [email protected] September 13, 2018 arXiv:astro-ph/0611590v2 8 Mar 2007 Manuscript: 36 pages, with 11 figures and 5 tables. 1 Proposed running head: Colors of Saturnian irregular satellites Corresponding author: Tommy Grav MS51, 60 Garden St. Cambridge, MA02138 USA Phone: (617) 384-7689 Fax: (617) 495-7093 Email: [email protected] 2 Abstract We have performed broadband color photometry of the twelve brightest irregular satellites of Saturn with the goal of understanding their surface composition, as well as their physical relationship. We find that the satellites have a wide variety of different surface colors, from the negative spectral slopes of the two retrograde satellites S IX Phoebe (S0 = −2:5 ± 0:4) and S XXV Mundilfari (S0 = −5:0 ± 1:9) to the fairly red slope of S XXII Ijiraq (S0 = 19:5 ± 0:9). We further find that there exist a correlation between dynamical families and spectral slope, with the prograde clusters, the Gallic and Inuit, showing tight clustering in colors among most of their members. The retrograde objects are dynamically and physically more dispersed, but some internal structure is apparent. Keywords: Irregular satellites; Photometry, Satellites, Surfaces; Saturn, Satellites. 3 1 Introduction The satellites of Saturn can be divided into two distinct groups, the regular and irregular, based on their orbital characteristics. -

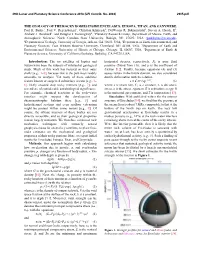
Exomoon Habitability Constrained by Illumination and Tidal Heating
submitted to Astrobiology: April 6, 2012 accepted by Astrobiology: September 8, 2012 published in Astrobiology: January 24, 2013 this updated draft: October 30, 2013 doi:10.1089/ast.2012.0859 Exomoon habitability constrained by illumination and tidal heating René HellerI , Rory BarnesII,III I Leibniz-Institute for Astrophysics Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany, [email protected] II Astronomy Department, University of Washington, Box 951580, Seattle, WA 98195, [email protected] III NASA Astrobiology Institute – Virtual Planetary Laboratory Lead Team, USA Abstract The detection of moons orbiting extrasolar planets (“exomoons”) has now become feasible. Once they are discovered in the circumstellar habitable zone, questions about their habitability will emerge. Exomoons are likely to be tidally locked to their planet and hence experience days much shorter than their orbital period around the star and have seasons, all of which works in favor of habitability. These satellites can receive more illumination per area than their host planets, as the planet reflects stellar light and emits thermal photons. On the contrary, eclipses can significantly alter local climates on exomoons by reducing stellar illumination. In addition to radiative heating, tidal heating can be very large on exomoons, possibly even large enough for sterilization. We identify combinations of physical and orbital parameters for which radiative and tidal heating are strong enough to trigger a runaway greenhouse. By analogy with the circumstellar habitable zone, these constraints define a circumplanetary “habitable edge”. We apply our model to hypothetical moons around the recently discovered exoplanet Kepler-22b and the giant planet candidate KOI211.01 and describe, for the first time, the orbits of habitable exomoons. -

Design of Low-Altitude Martian Orbits Using Frequency Analysis A
Design of Low-Altitude Martian Orbits using Frequency Analysis A. Noullez, K. Tsiganis To cite this version: A. Noullez, K. Tsiganis. Design of Low-Altitude Martian Orbits using Frequency Analysis. Advances in Space Research, Elsevier, 2021, 67, pp.477-495. 10.1016/j.asr.2020.10.032. hal-03007909 HAL Id: hal-03007909 https://hal.archives-ouvertes.fr/hal-03007909 Submitted on 16 Nov 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Design of Low-Altitude Martian Orbits using Frequency Analysis A. Noulleza,∗, K. Tsiganisb aUniversit´eC^oted'Azur, Observatoire de la C^oted'Azur, CNRS, Laboratoire Lagrange, bd. de l'Observatoire, C.S. 34229, 06304 Nice Cedex 4, France bSection of Astrophysics Astronomy & Mechanics, Department of Physics, Aristotle University of Thessaloniki, GR 541 24 Thessaloniki, Greece Abstract Nearly-circular Frozen Orbits (FOs) around axisymmetric bodies | or, quasi-circular Periodic Orbits (POs) around non-axisymmetric bodies | are of primary concern in the design of low-altitude survey missions. Here, we study very low-altitude orbits (down to 50 km) in a high-degree and order model of the Martian gravity field. We apply Prony's Frequency Analysis (FA) to characterize the time variation of their orbital elements by computing accurate quasi-periodic decompositions of the eccentricity and inclination vectors. -

JUICE Red Book
ESA/SRE(2014)1 September 2014 JUICE JUpiter ICy moons Explorer Exploring the emergence of habitable worlds around gas giants Definition Study Report European Space Agency 1 This page left intentionally blank 2 Mission Description Jupiter Icy Moons Explorer Key science goals The emergence of habitable worlds around gas giants Characterise Ganymede, Europa and Callisto as planetary objects and potential habitats Explore the Jupiter system as an archetype for gas giants Payload Ten instruments Laser Altimeter Radio Science Experiment Ice Penetrating Radar Visible-Infrared Hyperspectral Imaging Spectrometer Ultraviolet Imaging Spectrograph Imaging System Magnetometer Particle Package Submillimetre Wave Instrument Radio and Plasma Wave Instrument Overall mission profile 06/2022 - Launch by Ariane-5 ECA + EVEE Cruise 01/2030 - Jupiter orbit insertion Jupiter tour Transfer to Callisto (11 months) Europa phase: 2 Europa and 3 Callisto flybys (1 month) Jupiter High Latitude Phase: 9 Callisto flybys (9 months) Transfer to Ganymede (11 months) 09/2032 – Ganymede orbit insertion Ganymede tour Elliptical and high altitude circular phases (5 months) Low altitude (500 km) circular orbit (4 months) 06/2033 – End of nominal mission Spacecraft 3-axis stabilised Power: solar panels: ~900 W HGA: ~3 m, body fixed X and Ka bands Downlink ≥ 1.4 Gbit/day High Δv capability (2700 m/s) Radiation tolerance: 50 krad at equipment level Dry mass: ~1800 kg Ground TM stations ESTRAC network Key mission drivers Radiation tolerance and technology Power budget and solar arrays challenges Mass budget Responsibilities ESA: manufacturing, launch, operations of the spacecraft and data archiving PI Teams: science payload provision, operations, and data analysis 3 Foreword The JUICE (JUpiter ICy moon Explorer) mission, selected by ESA in May 2012 to be the first large mission within the Cosmic Vision Program 2015–2025, will provide the most comprehensive exploration to date of the Jovian system in all its complexity, with particular emphasis on Ganymede as a planetary body and potential habitat. -

First Stop on the Interstellar Journey: the Solar Gravity Lens Focus
1 DRAFT 16 May 2017 First Stop on the Interstellar Journey: The Solar Gravity Lens Focus Louis Friedman *1, Slava G. Turyshev2 1 Executive Director Emeritus, The Planetary Society 2 Jet Propulsion Laboratory, California Institute of Technology Abstract Whether or not Starshoti proves practical, it has focused attention on the technologies required for practical interstellar flight. They are: external energy (not in-space propulsion), sails (to be propelled by the external energy) and ultra-light spacecraft (so that the propulsion energy provides the largest possible increase in velocity). Much development is required in all three of these areas. The spacecraft technologies, nano- spacecraft and sails, can be developed through increasingly capable spacecraft that will be able of going further and faster through the interstellar medium. The external energy source (laser power in the Starshot concept) necessary for any flight beyond the solar system (>~100,000 AU) will be developed independently of the spacecraft. The solar gravity lens focus is a line beginning at approximately 547 AU from the Sun along the line defined by the identified exo-planet and the Sunii. An image of the exo-planet requires a coronagraph and telescope on the spacecraft, and an ability for the spacecraft to move around the focal line as it flies along it. The image is created in the “Einstein Ring” and extends several kilometers around the focal line – the spacecraft will have to collect pixels by maneuvering in the imageiii. This can be done over many years as the spacecraft flies along the focal line. The magnification by the solar gravity lens is a factor of 100 billion, permitting kilometer scale resolution of an exo-planet that might be even tens of light-years distant. -

Life Beyond Earth the Search for Habitable Worlds in the Universe
C:/ITOOLS/WMS/CUP-NEW/4181325/WORKINGFOLDER/COEN/9781107026179HTL.3D i [1–2] 27.6.2013 10:59AM Life Beyond Earth The Search for Habitable Worlds in the Universe With current missions to Mars and the Earth-like moon Titan, and many more missions planned, humankind stands on the verge of exciting progress and possible major discoveries in our quest for life in space. What is life and where can it exist? What searches are being made to identify conditions for life on other worlds? If extraterrestrial inhabited worlds are found, how can we explore them? Could humans survive beyond the Earth? In this book, two leading astrophysicists provide an engaging account of where we stand in our quest for habitable environments, in the Solar System and beyond. Starting from basic concepts, the narrative builds up scientifically, including more in-depth material as boxed additions to the main text. The authors recount fascinating recent discoveries, arising from space missions and from observations using ground-based telescopes, of possible life-related artefacts in Martian meteorites, of extrasolar planets, and of subsurface oceans on Europa, Titan and Enceladus. They also provide a forward look to exciting future missions, including the return to Venus, Mars and the Moon; further explorations of Pluto and Jupiter’s icy moons; and placing giant planet-seeking telescopes in orbit beyond Jupiter. showing how we approach the question of finding out whether the life that teems on our own planet is unique. This is an exciting, informative read for anyone interested in the search for habitable and inhabited planets, and makes an excellent primer for students keen to learn about astrobiology, habitability, planetary science and astronomy. -

The Inner Solar System Is the Name of the Terrestrial Planets and Asteroid
!"#$%&'''''''''''''''''''''''''''''''''' !"#$%&&#'$()*+'$(,-.#/ !"#$%&'(%#)*+,('% ()$&*++$,&-./",&-0-1$#&*-&1)$&+"#$&.2&1)$& 1$,,$-1,*"/&3/"+$1-&"+4&"-1$,.*4&5$/16&($,,$-1,*"/&*-& 78-1&"&2"+90&:"0&.2&-"0*+;&,.9<06&=*<$&1)$&>",1)?& 1$,,$-1,*"/&3/"+$1-&)"@$&"&9.,$&.2&*,.+&"+4&,.9<6 A1&1)$&9$+1$,&.2&1)$&-./",&-0-1$#&*-&1)$&B8+6& ()$&B8+&*-&"&5*;&5"//&.2&)04,.;$+&3.:$,$4&50& +89/$",&,$"91*.+-6&C"--*@$&$D3/.-*.+-&",$&;.*+;& .+&"//&.2&1)$&1*#$&*+-*4$&1)$&B8+6&E1F-&:)"1&#"<$-& 1)$&/*;)1&$@$,0&4"0&"+4&<$$3-&.8,&3/"+$1&:",#6& J.8&<+.:&:)"1&3/"+$1&*-&+$D16&J.8&/*@$&.+& =*;)1&G*3-&2,.#&1)$&B8+&1.&8-&*+&"5.81&$*;)1& *1H&J83?&1)$&>",1)&*-&+8#5$,&1),$$6&Q$&)"@$&"& #*+81$-6&()$&B8+&*-&1)$&#.-1&#"--*@$&1)*+;&*+&.8,& ,.9<0&*,.+&9.,$&"1&1)$&9$+1$,&.2&.8,&3/"+$16&Q$& -./",&-0-1$#6&E1&*-&-.&5*;&0.8&9.8/4&2*1&"5.81&"& )"@$&/*K8*4&:"1$,?&"+4&.8,&"*,&*-&#"4$&.2&#.-1/0& #*//*.+&>",1)-&*+-*4$&.2&*1H& +*1,.;$+&"+4&.D0;$+6&E1&1"<$-&1),$$&)8+4,$4&"+4& -*D10L2*@$&4"0-&2.,&8-&1.&9*,9/$&1)$&-8+6&Q$&.+/0& I/.-$-1&1.&1)$&B8+&*-&1)$&3/"+$1&C$,98,06& )"@$&.+$&#..+6 J.8&9.8/4&-K8$$G$&"5.81&$*;)1$$+&C$,98,0F-& *+-*4$&.2&>",1)6&E1&*-&#"4$&.2&#.-1/0&,.9<?&581&*1&)"-& !$D1&1.&8-&*+&*-&C",-6&C",-&"/-.&)"-&"&9.,$& "&)8;$&*,.+&9.,$&"+4&*1&;$+$,"1$-&"&5*;& .2&,.9<&"+4&*,.+6&E1&*-&"&/*11/$&#.,$&1)"+&)"/2&1)$& #";+$1*9&2*$/46&B3$$40&/*11/$&C$,98,0&-"*/-&",.8+4& -*G$&.2&>",1)6&()$&#.-1&4*-1*+91&2$"18,$&"5.81&C",-& 1)$&-8+&*+&.+/0&$*;)10L$*;)1&4"0-6&C$,98,0&:"-& *-&*1-&,$4&9./.,6&R8-1&,*9)&*+&*,.+&.D*4$&9.@$,-&1)$& 1)$&#$--$+;$,&.2&1)$&;.4-&*+&M.#"+)./.;0?& 3/"+$16&E1F-&-.,1&.2&/*<$&1)$&3/"+$1&*-&,8-1*+;6&Q)*1$&