Atomic Units E =H ¯ = Me = 1, Where Me Is the Mass of the Electron
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
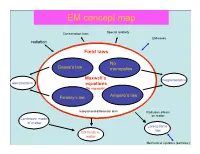
EM Concept Map
EM concept map Conservation laws Special relativity EM waves radiation Field laws No Gauss’s law monopoles ConservationMaxwell’s laws magnetostatics electrostatics equations (In vacuum) Faraday’s law Ampere’s law Integral and differential form Radiation effects on matter Continuum model of matter Lorenz force law EM fields in matter Mechanical systems (particles) Electricity and Magnetism PHYS-350: (updated Sept. 9th, (1605-1725 Monday, Wednesday, Leacock 109) 2010) Instructor: Shaun Lovejoy, Rutherford Physics, rm. 213, local Outline: 6537, email: [email protected]. 1. Vector Analysis: Tutorials: Tuesdays 4:15pm-5:15pm, location: the “Boardroom” Algebra, differential and integral calculus, curvilinear coordinates, (the southwest corner, ground floor of Rutherford physics). Office Hours: Thursday 4-5pm (either Lhermitte or Gervais, see Dirac function, potentials. the schedule on the course site). 2. Electrostatics: Teaching assistant: Julien Lhermitte, rm. 422, local 7033, email: Definitions, basic notions, laws, divergence and curl of the electric [email protected] potential, work and energy. Gervais, Hua Long, ERP-230, [email protected] 3. Special techniques: Math background: Prerequisites: Math 222A,B (Calculus III= Laplace's equation, images, seperation of variables, multipole multivariate calculus), 223A,B (Linear algebra), expansion. Corequisites: 314A (Advanced Calculus = vector 4. Electrostatic fields in matter: calculus), 315A (Ordinary differential equations) Polarization, electric displacement, dielectrics. Primary Course Book: "Introduction to Electrodynamics" by D. 5. Magnetostatics: J. Griffiths, Prentice-Hall, (1999, third edition). Lorenz force law, Biot-Savart law, divergence and curl of B, vector Similar books: potentials. -“Electromagnetism”, G. L. Pollack, D. R. Stump, Addison and 6. Magnetostatic fields in matter: Wesley, 2002. -

Magnetism, Magnetic Properties, Magnetochemistry
Magnetism, Magnetic Properties, Magnetochemistry 1 Magnetism All matter is electronic Positive/negative charges - bound by Coulombic forces Result of electric field E between charges, electric dipole Electric and magnetic fields = the electromagnetic interaction (Oersted, Maxwell) Electric field = electric +/ charges, electric dipole Magnetic field ??No source?? No magnetic charges, N-S No magnetic monopole Magnetic field = motion of electric charges (electric current, atomic motions) Magnetic dipole – magnetic moment = i A [A m2] 2 Electromagnetic Fields 3 Magnetism Magnetic field = motion of electric charges • Macro - electric current • Micro - spin + orbital momentum Ampère 1822 Poisson model Magnetic dipole – magnetic (dipole) moment [A m2] i A 4 Ampere model Magnetism Microscopic explanation of source of magnetism = Fundamental quantum magnets Unpaired electrons = spins (Bohr 1913) Atomic building blocks (protons, neutrons and electrons = fermions) possess an intrinsic magnetic moment Relativistic quantum theory (P. Dirac 1928) SPIN (quantum property ~ rotation of charged particles) Spin (½ for all fermions) gives rise to a magnetic moment 5 Atomic Motions of Electric Charges The origins for the magnetic moment of a free atom Motions of Electric Charges: 1) The spins of the electrons S. Unpaired spins give a paramagnetic contribution. Paired spins give a diamagnetic contribution. 2) The orbital angular momentum L of the electrons about the nucleus, degenerate orbitals, paramagnetic contribution. The change in the orbital moment -

An Introduction to Hartree-Fock Molecular Orbital Theory
An Introduction to Hartree-Fock Molecular Orbital Theory C. David Sherrill School of Chemistry and Biochemistry Georgia Institute of Technology June 2000 1 Introduction Hartree-Fock theory is fundamental to much of electronic structure theory. It is the basis of molecular orbital (MO) theory, which posits that each electron's motion can be described by a single-particle function (orbital) which does not depend explicitly on the instantaneous motions of the other electrons. Many of you have probably learned about (and maybe even solved prob- lems with) HucÄ kel MO theory, which takes Hartree-Fock MO theory as an implicit foundation and throws away most of the terms to make it tractable for simple calculations. The ubiquity of orbital concepts in chemistry is a testimony to the predictive power and intuitive appeal of Hartree-Fock MO theory. However, it is important to remember that these orbitals are mathematical constructs which only approximate reality. Only for the hydrogen atom (or other one-electron systems, like He+) are orbitals exact eigenfunctions of the full electronic Hamiltonian. As long as we are content to consider molecules near their equilibrium geometry, Hartree-Fock theory often provides a good starting point for more elaborate theoretical methods which are better approximations to the elec- tronic SchrÄodinger equation (e.g., many-body perturbation theory, single-reference con¯guration interaction). So...how do we calculate molecular orbitals using Hartree-Fock theory? That is the subject of these notes; we will explain Hartree-Fock theory at an introductory level. 2 What Problem Are We Solving? It is always important to remember the context of a theory. -

Modern Physics Unit 15: Nuclear Structure and Decay Lecture 15.1: Nuclear Characteristics
Modern Physics Unit 15: Nuclear Structure and Decay Lecture 15.1: Nuclear Characteristics Ron Reifenberger Professor of Physics Purdue University 1 Nucleons - the basic building blocks of the nucleus Also written as: 7 3 Li ~10-15 m Examples: A X=Chemical Element Z X Z = number of protons = atomic number 12 A = atomic mass number = Z+N 6 C N= A-Z = number of neutrons 35 17 Cl 2 What is the size of a nucleus? Three possibilities • Range of nuclear force? • Mass radius? • Charge radius? It turns out that for nuclear matter Nuclear force radius ≈ mass radius ≈ charge radius defines nuclear force range defines nuclear surface 3 Nuclear Charge Density The size of the lighter nuclei can be approximated by modeling the nuclear charge density ρ (C/m3): t ≈ 4.4a; a=0.54 fm 90% 10% Usually infer the best values for ρo, R and a for a given nucleus from scattering experiments 4 Nuclear mass density Scattering experiments indicate the nucleus is roughly spherical with a radius given by 1 3 −15 R = RRooA ; =1.07 × 10meters= 1.07 fm = 1.07 fermis A=atomic mass number What is the nuclear mass density of the most common isotope of iron? 56 26 Fe⇒= A56; Z = 26, N = 30 m Am⋅⋅3 Am 33A ⋅ m m ρ = nuc p= p= pp = o 1 33 VR4 3 3 3 44ππA R nuc π R 4(π RAo ) o o 3 3×× 1.66 10−27 kg = 3.2× 1017kg / m 3 4×× 3.14 (1.07 × 10−15m ) 3 The mass density is constant, independent of A! 5 Nuclear mass density for 27Al, 97Mo, 238U (from scattering experiments) (kg/m3) ρo heavy mass nucleus light mass nucleus middle mass nucleus 6 Typical Densities Material Density Helium 0.18 kg/m3 Air (dry) 1.2 kg/m3 Styrofoam ~100 kg/m3 Water 1000 kg/m3 Iron 7870 kg/m3 Lead 11,340 kg/m3 17 3 Nuclear Matter ~10 kg/m 7 Isotopes - same chemical element but different mass (J.J. -

Gauss' Linking Number Revisited
October 18, 2011 9:17 WSPC/S0218-2165 134-JKTR S0218216511009261 Journal of Knot Theory and Its Ramifications Vol. 20, No. 10 (2011) 1325–1343 c World Scientific Publishing Company DOI: 10.1142/S0218216511009261 GAUSS’ LINKING NUMBER REVISITED RENZO L. RICCA∗ Department of Mathematics and Applications, University of Milano-Bicocca, Via Cozzi 53, 20125 Milano, Italy [email protected] BERNARDO NIPOTI Department of Mathematics “F. Casorati”, University of Pavia, Via Ferrata 1, 27100 Pavia, Italy Accepted 6 August 2010 ABSTRACT In this paper we provide a mathematical reconstruction of what might have been Gauss’ own derivation of the linking number of 1833, providing also an alternative, explicit proof of its modern interpretation in terms of degree, signed crossings and inter- section number. The reconstruction presented here is entirely based on an accurate study of Gauss’ own work on terrestrial magnetism. A brief discussion of a possibly indepen- dent derivation made by Maxwell in 1867 completes this reconstruction. Since the linking number interpretations in terms of degree, signed crossings and intersection index play such an important role in modern mathematical physics, we offer a direct proof of their equivalence. Explicit examples of its interpretation in terms of oriented area are also provided. Keywords: Linking number; potential; degree; signed crossings; intersection number; oriented area. Mathematics Subject Classification 2010: 57M25, 57M27, 78A25 1. Introduction The concept of linking number was introduced by Gauss in a brief note on his diary in 1833 (see Sec. 2 below), but no proof was given, neither of its derivation, nor of its topological meaning. Its derivation remained indeed a mystery. -

Optical Properties of Bulk and Nano
Lecture 3: Optical Properties of Bulk and Nano 5 nm Course Info First H/W#1 is due Sept. 10 The Previous Lecture Origin frequency dependence of χ in real materials • Lorentz model (harmonic oscillator model) e- n(ω) n' n'' n'1= ω0 + Nucleus ω0 ω Today optical properties of materials • Insulators (Lattice absorption, color centers…) • Semiconductors (Energy bands, Urbach tail, excitons …) • Metals (Response due to bound and free electrons, plasma oscillations.. ) Optical properties of molecules, nanoparticles, and microparticles Classification Matter: Insulators, Semiconductors, Metals Bonds and bands • One atom, e.g. H. Schrödinger equation: E H+ • Two atoms: bond formation ? H+ +H Every electron contributes one state • Equilibrium distance d (after reaction) Classification Matter ~ 1 eV • Pauli principle: Only 2 electrons in the same electronic state (one spin & one spin ) Classification Matter Atoms with many electrons Empty outer orbitals Outermost electrons interact Form bands Partly filled valence orbitals Filled Energy Inner Electrons in inner shells do not interact shells Do not form bands Distance between atoms Classification Matter Insulators, semiconductors, and metals • Classification based on bandstructure Dispersion and Absorption in Insulators Electronic transitions No transitions Atomic vibrations Refractive Index Various Materials 3.4 3.0 2.0 Refractive index: n’ index: Refractive 1.0 0.1 1.0 10 λ (µm) Color Centers • Insulators with a large EGAP should not show absorption…..or ? • Ion beam irradiation or x-ray exposure result in beautiful colors! • Due to formation of color (absorption) centers….(Homework assignment) Absorption Processes in Semiconductors Absorption spectrum of a typical semiconductor E EC Phonon Photon EV ωPhonon Excitons: Electron and Hole Bound by Coulomb Analogy with H-atom • Electron orbit around a hole is similar to the electron orbit around a H-core • 1913 Niels Bohr: Electron restricted to well-defined orbits n = 1 + -13.6 eV n = 2 n = 3 -3.4 eV -1.51 eV me4 13.6 • Binding energy electron: =−=−=e EB 2 2 eV, n 1,2,3,.. -

On the Covariant Representation of Integral Equations of the Electromagnetic Field
On the covariant representation of integral equations of the electromagnetic field Sergey G. Fedosin PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia E-mail: [email protected] Gauss integral theorems for electric and magnetic fields, Faraday’s law of electromagnetic induction, magnetic field circulation theorem, theorems on the flux and circulation of vector potential, which are valid in curved spacetime, are presented in a covariant form. Covariant formulas for magnetic and electric fluxes, for electromotive force and circulation of the vector potential are provided. In particular, the electromotive force is expressed by a line integral over a closed curve, while in the integral, in addition to the vortex electric field strength, a determinant of the metric tensor also appears. Similarly, the magnetic flux is expressed by a surface integral from the product of magnetic field induction by the determinant of the metric tensor. A new physical quantity is introduced – the integral scalar potential, the rate of change of which over time determines the flux of vector potential through a closed surface. It is shown that the commonly used four-dimensional Kelvin-Stokes theorem does not allow one to deduce fully the integral laws of the electromagnetic field and in the covariant notation requires the addition of determinant of the metric tensor, besides the validity of the Kelvin-Stokes theorem is limited to the cases when determinant of metric tensor and the contour area are independent from time. This disadvantage is not present in the approach that uses the divergence theorem and equation for the dual electromagnetic field tensor. -

Lord Kelvin and the Age of the Earth.Pdf
ME201/MTH281/ME400/CHE400 Lord Kelvin and the Age of the Earth Lord Kelvin (1824 - 1907) 1. About Lord Kelvin Lord Kelvin was born William Thomson in Belfast Ireland in 1824. He attended Glasgow University from the age of 10, and later took his BA at Cambridge. He was appointed Professor of Natural Philosophy at Glasgow in 1846, a position he retained the rest of his life. He worked on a broad range of topics in physics, including thermody- namics, electricity and magnetism, hydrodynamics, atomic physics, and earth science. He also had a strong interest in practical problems, and in 1866 he was knighted for his work on the transtlantic cable. In 1892 he became Baron Kelvin, and this name survives as the name of the absolute temperature scale which he proposed in 1848. During his long career, Kelvin published more than 600 papers. He was elected to the Royal Society in 1851, and served as president of that organization from 1890 to 1895. The information in this section and the picture above were taken from a very useful web site called the MacTu- tor History of Mathematics Archive, sponsored by St. Andrews University. The web address is http://www-history.mcs.st-and.ac.uk/~history/ 2 kelvin.nb 2. The Age of the Earth The earth shows it age in many ways. Some techniques for estimating this age require us to observe the present state of a time-dependent process, and from that observation infer the time at which the process started. If we believe that the process started when the earth was formed, we get an estimate of the earth's age. -

Units and Magnitudes (Lecture Notes)
physics 8.701 topic 2 Frank Wilczek Units and Magnitudes (lecture notes) This lecture has two parts. The first part is mainly a practical guide to the measurement units that dominate the particle physics literature, and culture. The second part is a quasi-philosophical discussion of deep issues around unit systems, including a comparison of atomic, particle ("strong") and Planck units. For a more extended, profound treatment of the second part issues, see arxiv.org/pdf/0708.4361v1.pdf . Because special relativity and quantum mechanics permeate modern particle physics, it is useful to employ units so that c = ħ = 1. In other words, we report velocities as multiples the speed of light c, and actions (or equivalently angular momenta) as multiples of the rationalized Planck's constant ħ, which is the original Planck constant h divided by 2π. 27 August 2013 physics 8.701 topic 2 Frank Wilczek In classical physics one usually keeps separate units for mass, length and time. I invite you to think about why! (I'll give you my take on it later.) To bring out the "dimensional" features of particle physics units without excess baggage, it is helpful to keep track of powers of mass M, length L, and time T without regard to magnitudes, in the form When these are both set equal to 1, the M, L, T system collapses to just one independent dimension. So we can - and usually do - consider everything as having the units of some power of mass. Thus for energy we have while for momentum 27 August 2013 physics 8.701 topic 2 Frank Wilczek and for length so that energy and momentum have the units of mass, while length has the units of inverse mass. -

Lecture #4, Matter/Energy Interactions, Emissions Spectra, Quantum Numbers
Welcome to 3.091 Lecture 4 September 16, 2009 Matter/Energy Interactions: Atomic Spectra 3.091 Periodic Table Quiz 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 Name Grade /10 Image by MIT OpenCourseWare. Rutherford-Geiger-Marsden experiment Image by MIT OpenCourseWare. Bohr Postulates for the Hydrogen Atom 1. Rutherford atom is correct 2. Classical EM theory not applicable to orbiting e- 3. Newtonian mechanics applicable to orbiting e- 4. Eelectron = Ekinetic + Epotential 5. e- energy quantized through its angular momentum: L = mvr = nh/2π, n = 1, 2, 3,… 6. Planck-Einstein relation applies to e- transitions: ΔE = Ef - Ei = hν = hc/λ c = νλ _ _ 24 1 18 Bohr magneton µΒ = eh/2me 9.274 015 4(31) X 10 J T 0.34 _ _ 27 1 19 Nuclear magneton µΝ = eh/2mp 5.050 786 6(17) X 10 J T 0.34 _ 2 3 20 Fine structure constant α = µ0ce /2h 7.297 353 08(33) X 10 0.045 21 Inverse fine structure constant 1/α 137.035 989 5(61) 0.045 _ 2 1 22 Rydberg constant R¥ = mecα /2h 10 973 731.534(13) m 0.0012 23 Rydberg constant in eV R¥ hc/{e} 13.605 698 1(40) eV 0.30 _ 10 24 Bohr radius a0 = a/4πR¥ 0.529 177 249(24) X 10 m 0.045 _ _ 4 2 1 25 Quantum of circulation h/2me 3.636 948 07(33) X 10 m s 0.089 _ 11 1 26 Electron specific charge -e/me -1.758 819 62(53) X 10 C kg 0.30 _ 12 27 Electron Compton wavelength λC = h/mec 2.426 310 58(22) X 10 m 0.089 _ 2 15 28 Electron classical radius re = α a0 2.817 940 92(38) X 10 m 0.13 _ _ 26 1 29 Electron magnetic moment` µe 928.477 01(31) X 10 J T 0.34 _ _ 3 30 Electron mag. -

Bohr Model of Hydrogen
Chapter 3 Bohr model of hydrogen Figure 3.1: Democritus The atomic theory of matter has a long history, in some ways all the way back to the ancient Greeks (Democritus - ca. 400 BCE - suggested that all things are composed of indivisible \atoms"). From what we can observe, atoms have certain properties and behaviors, which can be summarized as follows: Atoms are small, with diameters on the order of 0:1 nm. Atoms are stable, they do not spontaneously break apart into smaller pieces or collapse. Atoms contain negatively charged electrons, but are electrically neutral. Atoms emit and absorb electromagnetic radiation. Any successful model of atoms must be capable of describing these observed properties. 1 (a) Isaac Newton (b) Joseph von Fraunhofer (c) Gustav Robert Kirch- hoff 3.1 Atomic spectra Even though the spectral nature of light is present in a rainbow, it was not until 1666 that Isaac Newton showed that white light from the sun is com- posed of a continuum of colors (frequencies). Newton introduced the term \spectrum" to describe this phenomenon. His method to measure the spec- trum of light consisted of a small aperture to define a point source of light, a lens to collimate this into a beam of light, a glass spectrum to disperse the colors and a screen on which to observe the resulting spectrum. This is indeed quite close to a modern spectrometer! Newton's analysis was the beginning of the science of spectroscopy (the study of the frequency distri- bution of light from different sources). The first observation of the discrete nature of emission and absorption from atomic systems was made by Joseph Fraunhofer in 1814. -

Particle Nature of Matter
Solved Problems on the Particle Nature of Matter Charles Asman, Adam Monahan and Malcolm McMillan Department of Physics and Astronomy University of British Columbia, Vancouver, British Columbia, Canada Fall 1999; revised 2011 by Malcolm McMillan Given here are solutions to 5 problems on the particle nature of matter. The solutions were used as a learning-tool for students in the introductory undergraduate course Physics 200 Relativity and Quanta given by Malcolm McMillan at UBC during the 1998 and 1999 Winter Sessions. The solutions were prepared in collaboration with Charles Asman and Adam Monaham who were graduate students in the Department of Physics at the time. The problems are from Chapter 3 The Particle Nature of Matter of the course text Modern Physics by Raymond A. Serway, Clement J. Moses and Curt A. Moyer, Saunders College Publishing, 2nd ed., (1997). Coulomb's Constant and the Elementary Charge When solving numerical problems on the particle nature of matter it is useful to note that the product of Coulomb's constant k = 8:9876 × 109 m2= C2 (1) and the square of the elementary charge e = 1:6022 × 10−19 C (2) is ke2 = 1:4400 eV nm = 1:4400 keV pm = 1:4400 MeV fm (3) where eV = 1:6022 × 10−19 J (4) Breakdown of the Rutherford Scattering Formula: Radius of a Nucleus Problem 3.9, page 39 It is observed that α particles with kinetic energies of 13.9 MeV or higher, incident on copper foils, do not obey Rutherford's (sin φ/2)−4 scattering formula. • Use this observation to estimate the radius of the nucleus of a copper atom.