Memory-Efficient Fixpoint Computation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Event-Driven Embedded Operating System for Miniature Robots
This is a repository copy of OpenSwarm: an event-driven embedded operating system for miniature robots. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/110437/ Version: Accepted Version Proceedings Paper: Trenkwalder, S.M., Lopes, Y.K., Kolling, A. et al. (3 more authors) (2016) OpenSwarm: an event-driven embedded operating system for miniature robots. In: Proceedings of IROS 2016. 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems, 09-14 Oct 2016, Daejeon, Korea. IEEE . ISBN 978-1-5090-3762-9 https://doi.org/10.1109/IROS.2016.7759660 © 2016 IEEE. Personal use of this material is permitted. Permission from IEEE must be obtained for all other users, including reprinting/ republishing this material for advertising or promotional purposes, creating new collective works for resale or redistribution to servers or lists, or reuse of any copyrighted components of this work in other works. Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. -

What Are the Problems with Embedded Linux?
What Are the Problems with Embedded Linux? Every Operating System Has Benefits and Drawbacks Linux is ubiquitous. It runs most internet servers, is inside Android* smartphones, and is used on millions of embedded systems that, in the past, ran Real-Time Operating Systems (RTOSes). Linux can (and should) be used were possible for embedded projects, but while it gives you extreme choice, it also presents the risk of extreme complexity. What, then, are the trade-offs between embedded Linux and an RTOS? In this article, we cover some key considerations when evaluating Linux for a new development: ■ Design your system architecture first ■ What is Linux? ■ Linux vs. RTOSes ■ Free software is about liberty—not price ■ How much does Embedded Linux cost? ■ Why pay for Embedded Linux? ■ Should you buy Embedded Linux or roll-your-own (RYO)? ■ To fork or not to fork? ■ Software patching ■ Open source licensing ■ Making an informed decision The important thing is not whether Linux or an RTOS is “the best,” but whether either operating system—or both together—makes the most technical and financial sense for your project. We hope this article helps you make an informed decision. Design Your System Architecture First It is important to design your system architecture first—before choosing either Linux or an RTOS—because both choices can limit architectural freedom. You may discover that aspects of your design require neither Linux nor an RTOS, making your design a strong candidate for a heterogeneous approach that includes one or more bare-metal environments (with possibly a Linux and/or RTOS environment as well). -

Co-Optimizing Performance and Memory Footprint Via Integrated CPU/GPU Memory Management, an Implementation on Autonomous Driving Platform
2020 IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS) Co-Optimizing Performance and Memory Footprint Via Integrated CPU/GPU Memory Management, an Implementation on Autonomous Driving Platform Soroush Bateni*, Zhendong Wang*, Yuankun Zhu, Yang Hu, and Cong Liu The University of Texas at Dallas Abstract—Cutting-edge embedded system applications, such as launches the OpenVINO toolkit for the edge-based deep self-driving cars and unmanned drone software, are reliant on learning inference on its integrated HD GPUs [4]. integrated CPU/GPU platforms for their DNNs-driven workload, Despite the advantages in SWaP features presented by the such as perception and other highly parallel components. In this work, we set out to explore the hidden performance im- integrated CPU/GPU architecture, our community still lacks plication of GPU memory management methods of integrated an in-depth understanding of the architectural and system CPU/GPU architecture. Through a series of experiments on behaviors of integrated GPU when emerging autonomous and micro-benchmarks and real-world workloads, we find that the edge intelligence workloads are executed, particularly in multi- performance under different memory management methods may tasking fashion. Specifically, in this paper we set out to explore vary according to application characteristics. Based on this observation, we develop a performance model that can predict the performance implications exposed by various GPU memory system overhead for each memory management method based management (MM) methods of the integrated CPU/GPU on application characteristics. Guided by the performance model, architecture. The reason we focus on the performance impacts we further propose a runtime scheduler. -

Performance Study of Real-Time Operating Systems for Internet Of
IET Software Research Article ISSN 1751-8806 Performance study of real-time operating Received on 11th April 2017 Revised 13th December 2017 systems for internet of things devices Accepted on 13th January 2018 E-First on 16th February 2018 doi: 10.1049/iet-sen.2017.0048 www.ietdl.org Rafael Raymundo Belleza1 , Edison Pignaton de Freitas1 1Institute of Informatics, Federal University of Rio Grande do Sul, Av. Bento Gonçalves, 9500, CP 15064, Porto Alegre CEP: 91501-970, Brazil E-mail: [email protected] Abstract: The development of constrained devices for the internet of things (IoT) presents lots of challenges to software developers who build applications on top of these devices. Many applications in this domain have severe non-functional requirements related to timing properties, which are important concerns that have to be handled. By using real-time operating systems (RTOSs), developers have greater productivity, as they provide native support for real-time properties handling. Some of the key points in the software development for IoT in these constrained devices, like task synchronisation and network communications, are already solved by this provided real-time support. However, different RTOSs offer different degrees of support to the different demanded real-time properties. Observing this aspect, this study presents a set of benchmark tests on the selected open source and proprietary RTOSs focused on the IoT. The benchmark results show that there is no clear winner, as each RTOS performs well at least on some criteria, but general conclusions can be drawn on the suitability of each of them according to their performance evaluation in the obtained results. -

Our Tas Top 11 Technologies of the Decade Tinyos and Nesc Hardware Evolu On
Our TAs Top 11 Technologies of the Decade Mo Sha Yong Fu 1.! Smartphones 7.! Drone Aircra • [email protected]" •! [email protected]" •! TinyOS tutorial." •! Grade critiques." 2.! Social Networking 8.! Planetary Rovers •! Help students with projects." •! Office Hour: by appointment." 3.! Voice over IP 9.! Flexible AC •! Manage motes." •! Bryan 502D Transmission •! Grade projects." 4.! LED Lighng •! Office Hour: Tue/Thu 5:30-6." 5.! Mul@core CPUs 10.!Digital Photography •! Bryan 502A 6.! Cloud Compung 11.!Class-D Audio Chenyang Lu 1 Chenyang Lu 2 TinyOS and nesC Hardware Evoluon ! TinyOS: OS for wireless sensor networks. ! Miniature devices manufactured economically ! nesC: programming language for TinyOS. ! Microprocessors ! Sensors/actuators ! Wireless chips 4.5’’X2.4’’ 1’’X1’’ 1 mm2 1 nm2 Chenyang Lu 4 Chenyang Lu 3 Mica2 Mote Hardware Constraints ! Processor ! Microcontroller: 7.4 MHz, 8 bit Severe constraints on power, size, and cost ! Memory: 4KB data, 128 KB program ! slow microprocessor ! Radio ! low-bandwidth radio ! Max 38.4 Kbps ! limited memory ! Sensors ! limited hardware parallelism CPU hit by many interrupts! ! Light, temperature, acceleraon, acous@c, magne@c… ! manage sleep modes in hardware components ! Power ! <1 week on two AA baeries in ac@ve mode ! >1 year baery life on sleep modes! Chenyang Lu 5 Chenyang Lu 6 Soware Challenges Tradional OS ! Small memory footprint ! Mul@-threaded ! Efficiency - power and processing ! Preemp@ve scheduling ! Concurrency-intensive operaons ! Threads: ! Diversity in applicaons & plaorm efficient modularity ! ready to run; ! Support reconfigurable hardware and soJware executing ! execu@ng on the CPU; ! wai@ng for data. gets CPU preempted needs data gets data ready waiting needs data Chenyang Lu 7 Chenyang Lu 8 Pros and Cons of Tradional OS Example: Preempve Priority Scheduling ! Each process has a fixed priority (1 highest); ! Mul@-threaded + preemp@ve scheduling ! P1: priority 1; P2: priority 2; P3: priority 3. -

Building for I.MX Mature Boards
NXP Semiconductors Document Number: AN12024 Application Notes Rev. 0 , 07/2017 Building for i.MX Mature Boards 1. Introduction Contents The software for mature i.MX boards is upstreamed into 1. Introduction ........................................................................ 1 the Linux Kernel and U-Boot communities. These 2. Mature SoC Software Status .............................................. 2 boards can use the current Linux Kernel and U-Boot 3. Further Assistance .............................................................. 2 4. Boards Supported by the Yocto Project Community ......... 2 community solution. NXP no longer provides code and 4.1. Build environment setup ......................................... 3 images for these boards directly. This document 4.2. Examples ................................................................ 3 describes how to build the current Linux kernel and U- Boot software using the community solution for mature boards. The i.MX Board Support Packages (BSP) Releases are only supported for one year after the release date, so developing mature SoC projects using community solutions provides more current software and longer life for software than using the static BSPs provided by NXP. Community software includes upstreamed patches that the i.MX development team has provided to the community after the BSPs were released. Peripherals on i.MX mature boards such as the VPU and GPU, which depend on proprietary software, might be limited to an earlier version of the i.MX BSP. Supported i.MX reference boards should use the latest released i.MX BSPs on i.MX Software and Tools. Community solutions are not formally validated for i.MX. © 2017 NXP B.V. Boards Supported by the Yocto Project Community 2. Mature SoC Software Status The following i.MX mature SoC boards are from the i.MX 2X, 3X, and 5X families. -

Timing Comparison of the Real-Time Operating Systems for Small Microcontrollers
S S symmetry Article Timing Comparison of the Real-Time Operating Systems for Small Microcontrollers Ioan Ungurean 1,2 1 Faculty of Electrical Engineering and Computer Science; Stefan cel Mare University of Suceava, 720229 Suceava, Romania; [email protected] 2 MANSiD Integrated Center, Stefan cel Mare University, 720229 Suceava, Romania Received: 9 March 2020; Accepted: 1 April 2020; Published: 8 April 2020 Abstract: In automatic systems used in the control and monitoring of industrial processes, fieldbuses with specific real-time requirements are used. Often, the sensors are connected to these fieldbuses through embedded systems, which also have real-time features specific to the industrial environment in which it operates. The embedded operating systems are very important in the design and development of embedded systems. A distinct class of these operating systems is real-time operating systems (RTOSs) that can be used to develop embedded systems, which have hard and/or soft real-time requirements on small microcontrollers (MCUs). RTOSs offer the basic support for developing embedded systems with applicability in a wide range of fields such as data acquisition, internet of things, data compression, pattern recognition, diversity, similarity, symmetry, and so on. The RTOSs provide basic services for multitasking applications with deterministic behavior on MCUs. The services provided by the RTOSs are task management and inter-task synchronization and communication. The selection of the RTOS is very important in the development of the embedded system with real-time requirements and it must be based on the latency in the handling of the critical operations triggered by internal or external events, predictability/determinism in the execution of the RTOS primitives, license costs, and memory footprint. -
Exploiting Data Similarity to Reduce Memory Footprints
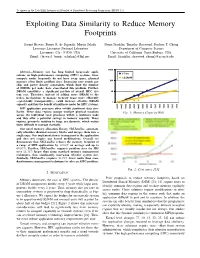
To appear in the 25th IEEE International Parallel & Distributed Processing Symposium (IPDPS’11) Exploiting Data Similarity to Reduce Memory Footprints Susmit Biswas, Bronis R. de Supinski, Martin Schulz Diana Franklin, Timothy Sherwood, Frederic T. Chong Lawrence Livermore National Laboratory Department of Computer Science Livermore, CA - 94550, USA University of California, Santa Barbara, USA Email: fbiswas3, bronis, [email protected] Email: ffranklin, sherwood, [email protected] Abstract—Memory size has long limited large-scale appli- cations on high-performance computing (HPC) systems. Since compute nodes frequently do not have swap space, physical memory often limits problem sizes. Increasing core counts per chip and power density constraints, which limit the number of DIMMs per node, have exacerbated this problem. Further, DRAM constitutes a significant portion of overall HPC sys- tem cost. Therefore, instead of adding more DRAM to the nodes, mechanisms to manage memory usage more efficiently —preferably transparently— could increase effective DRAM capacity and thus the benefit of multicore nodes for HPC systems. MPI application processes often exhibit significant data sim- ilarity. These data regions occupy multiple physical locations Fig. 1: Memory Capacity Wall across the individual rank processes within a multicore node and thus offer a potential savings in memory capacity. These regions, primarily residing in heap, are dynamic, which makes them difficult to manage statically. Our novel memory allocation library, SBLLmalloc, automati- cally identifies identical memory blocks and merges them into a single copy. Our implementation is transparent to the application and does not require any kernel modifications. Overall, we demonstrate that SBLLmalloc reduces the memory footprint of a range of MPI applications by 32:03% on average and up to 60:87%. -

PSA Firmware Update API 0.7
PSA Firmware Update API 0.7 Document number: IHI 0093 Release Quality: Beta Issue Number: 0 Confidentiality: Non-confidential Date of Issue: 04/02/2021 Copyright © 2020-2021, Arm Limited. All rights reserved. Abstract This manual defines a standard firmware interface for installing firmware updates. Note: This is a Beta quality release. The content is subject to change. Feedback should be sent to [email protected] Contents About this document v Release information v Arm Non-Confidential Document Licence (“Licence”) vi References viii Terms and abbreviations viii Conventions x Typographical conventions x Numbers x Feedback xi Feedback on this book xi 1 Introduction 12 2 Design goals 13 2.1 Suitable for constrained devices 13 2.2 PSA Root of Trust update 13 2.3 Application Root of Trust update 14 2.4 Flexiblility for different trust models 14 2.5 Protocol independence 14 2.6 Transport independence 14 2.7 Hardware flexibility 15 2.8 Composite devices 15 2.9 Room for different implementations 15 3 Terminology 16 3.1 Image 16 3.2 Trust anchor 16 3.3 Installer 17 3.4 Update client 18 IHI 0093 Copyright © 2020-2021, Arm Limited or its affiliates. All rights reserved. Page i 0.7 Beta (Issue 0) Non-confidential 3.5 Secure Processing Environment (SPE) 18 3.6 Staging area 18 4 Trust model and scenarios 19 5 Design overview 20 5.1 Mandatory functions 20 5.1.1 Querying installed images 20 5.1.2 Image storing 20 5.1.3 Metadata storage 21 5.1.4 Verify image 21 5.1.5 Triggering a reboot 21 5.2 Optional functions 21 5.3 State transitions for an image 22 5.4 -

Yocto Project Reference Manual Is for the 1.4.3 Release of the Yocto Project
Richard Purdie, Linux Foundation <[email protected]> by Richard Purdie Copyright © 2010-2014 Linux Foundation Permission is granted to copy, distribute and/or modify this document under the terms of the Creative Commons Attribution-Share Alike 2.0 UK: England & Wales [http://creativecommons.org/licenses/by-sa/2.0/uk/] as published by Creative Commons. Manual Notes • This version of the Yocto Project Reference Manual is for the 1.4.3 release of the Yocto Project. To be sure you have the latest version of the manual for this release, go to the Yocto Project documentation page [http://www.yoctoproject.org/documentation] and select the manual from that site. Manuals from the site are more up-to-date than manuals derived from the Yocto Project released TAR files. • If you located this manual through a web search, the version of the manual might not be the one you want (e.g. the search might have returned a manual much older than the Yocto Project version with which you are working). You can see all Yocto Project major releases by visiting the Releases [https://wiki.yoctoproject.org/wiki/Releases] page. If you need a version of this manual for a different Yocto Project release, visit the Yocto Project documentation page [http://www.yoctoproject.org/ documentation] and select the manual set by using the "ACTIVE RELEASES DOCUMENTATION" or "DOCUMENTS ARCHIVE" pull-down menus. • To report any inaccuracies or problems with this manual, send an email to the Yocto Project discussion group at [email protected] or log into the freenode #yocto channel. -

Workshop TP5 Root of Trust.Pdf
Root of Trust in the Physical Internet Keywords: Root of Trust, Secure Firmware Update, Physical Internet, Internet of Things Contribution Form: Research Paper Word count: 999 1. Building Trust in Physical Internet Analogous to the Internet of computers whereas digital content is routed in a highly efficient way the Physical Internet (PI) aims to increase the efficiency of transportation of physical objects. Likewise a global system PI is „based on the interconnection of logistics networks by a standardized set of collaboration protocols, modular containers and smart interfaces” (Ballot et al., 2014, p. 23). The high order of collaboration requires a solid foundation of trust. This raises the question ‚How trust can be built in the Physical Internet?‘. Regarding the rapid expansion of the Internet to objects of our everyday life, the Internet-of-Things (IoT) closes the gap between the physical and the digital world (Mattern, 2010). Hence, the IoT is not only an enabling technology but an integral part of the PI (Montreuil, 2015). Breaking down to the smallest unit, smart tags, tiny, battery operated computers equipped with sensing, communication, data storage and processing capabilities connect the physical and the digital world. The more capable the more vulnerable to attacks smart tags become. Once compromised a single smart tag can open criminals not only container padlocks but also grant them access to the higher level systems e.g. logistics information systems. In order to build trust in the PI, we propose a model to protect the ‚root tip’ of IoT and PI, the smart tag firmware. 2. Root of trust and Secure Firmware Update Root of Trust refers to a „system element that provides services, including verification of system, software and data integrity and confidentiality, and data (software and information) integrity attestation between other trusted devices in a system or network.“ (Casper, 2011). -

Insights Into Webassembly: Compilation Performance and Shared Code Caching in Node.Js
Insights into WebAssembly: Compilation Performance and Shared Code Caching in Node.js Tobias Nießen Michael Dawson Faculty of Computer Science IBM Runtime Technologies University of New Brunswick IBM Canada [email protected] [email protected] Panos Patros Kenneth B. Kent Software Engineering Faculty of Computer Science University of Waikato University of New Brunswick [email protected] [email protected] ABSTRACT high-level languages, the WebAssembly instruction set is closely re- Alongside JavaScript, V8 and Node.js have become essential com- lated to actual instruction sets of modern processors, since the initial ponents of contemporary web and cloud applications. With the WebAssembly specification does not contain high-level concepts addition of WebAssembly to the web, developers finally have a fast such as objects or garbage collection [8]. Because of the similarity of platform for performance-critical code. However, this addition also the WebAssembly instruction set to physical processor instruction introduces new challenges to client and server applications. New sets, many existing “low-level” languages can already be compiled application architectures, such as serverless computing, require to WebAssembly, including C, C++, and Rust. instantaneous performance without long startup times. In this pa- WebAssembly also features an interesting combination of secu- per, we investigate the performance of WebAssembly compilation rity properties. By design, WebAssembly can only interact with its in V8 and Node.js, and present the design and implementation of host environment through an application-specific interface. There a multi-process shared code cache for Node.js applications. We is no built-in concept of system calls, but they can be implemented demonstrate how such a cache can significantly increase applica- through explicitly imported functions.