The Field of P-Adic Numbers, Absolute Values, Ostrowski's Theorem for Q
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![OSTROWSKI for NUMBER FIELDS 1. Introduction in 1916, Ostrowski [6] Classified the Nontrivial Absolute Values on Q: up to Equival](https://docslib.b-cdn.net/cover/4979/ostrowski-for-number-fields-1-introduction-in-1916-ostrowski-6-classified-the-nontrivial-absolute-values-on-q-up-to-equival-154979.webp)
OSTROWSKI for NUMBER FIELDS 1. Introduction in 1916, Ostrowski [6] Classified the Nontrivial Absolute Values on Q: up to Equival
OSTROWSKI FOR NUMBER FIELDS KEITH CONRAD 1. Introduction In 1916, Ostrowski [6] classified the nontrivial absolute values on Q: up to equivalence, they are the usual (archimedean) absolute value and the p-adic absolute values for different primes p, with none of these being equivalent to each other. We will see how this theorem extends to a number field K, giving a list of all the nontrivial absolute values on K up to equivalence: for each nonzero prime ideal p in OK there is a p-adic absolute value, real embeddings of K and complex embeddings of K up to conjugation lead to archimedean absolute values on K, and every nontrivial absolute value on K is equivalent to a p-adic, real, or complex absolute value. 2. Defining nontrivial absolute values on K For each nonzero prime ideal p in OK , a p-adic absolute value on K is defined in terms × of a p-adic valuation ordp that is first defined on OK − f0g and extended to K by taking ratios. m Definition 2.1. For x 2 OK − f0g, define ordp(x) := m where xOK = p a with m ≥ 0 and p - a. We have ordp(xy) = ordp(x)+ordp(y) for nonzero x and y in OK by unique factorization of × ideals in OK . This lets us extend ordp to K by using ratios of nonzero numbers in OK : for × α 2 K , write α = x=y for nonzero x and y in OK and set ordp(α) := ordp(x) − ordp(y). To 0 0 0 0 0 0 see this is well-defined, if x=y = x =y for nonzero x; y; x , and y in OK then xy = x y 0 0 in OK , which implies ordp(x) + ordp(y ) = ordp(x ) + ordp(y), so ordp(x) − ordp(y) = 0 0 × × ordp(x ) − ordp(y ). -

1 Absolute Values and Valuations
Algebra in positive Characteristic Fr¨uhjahrssemester 08 Lecturer: Prof. R. Pink Organizer: P. Hubschmid Absolute values, valuations and completion F. Crivelli ([email protected]) April 21, 2008 Introduction During this talk I’ll introduce the basic definitions and some results about valuations, absolute values of fields and completions. These notions will give two basic examples: the rational function field Fq(T ) and the field Qp of the p-adic numbers. 1 Absolute values and valuations All along this section, K denote a field. 1.1 Absolute values We begin with a well-known Definition 1. An absolute value of K is a function | | : K → R satisfying these properties, ∀ x, y ∈ K: 1. |x| = 0 ⇔ x = 0, 2. |x| ≥ 0, 3. |xy| = |x| |y|, 4. |x + y| ≤ |x| + |y|. (Triangle inequality) Note that if we set |x| = 1 for all 0 6= x ∈ K and |0| = 0, we have an absolute value on K, called the trivial absolute value. From now on, when we speak about an absolute value | |, we assume that | | is non-trivial. Moreover, if we define d : K × K → R by d(x, y) = |x − y|, x, y ∈ K, d is a metric on K and we have a topological structure on K. We have also some basic properties that we can deduce directly from the definition of an absolute value. 1 Lemma 1. Let | | be an absolute value on K. We have 1. |1| = 1, 2. |ζ| = 1, for all ζ ∈ K with ζd = 1 for some 0 6= d ∈ N (ζ is a root of unity), 3. -
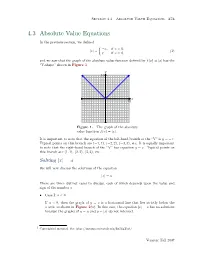
4.3 Absolute Value Equations 373
Section 4.3 Absolute Value Equations 373 4.3 Absolute Value Equations In the previous section, we defined −x, if x < 0. |x| = (1) x, if x ≥ 0, and we saw that the graph of the absolute value function defined by f(x) = |x| has the “V-shape” shown in Figure 1. y 10 x 10 Figure 1. The graph of the absolute value function f(x) = |x|. It is important to note that the equation of the left-hand branch of the “V” is y = −x. Typical points on this branch are (−1, 1), (−2, 2), (−3, 3), etc. It is equally important to note that the right-hand branch of the “V” has equation y = x. Typical points on this branch are (1, 1), (2, 2), (3, 3), etc. Solving |x| = a We will now discuss the solutions of the equation |x| = a. There are three distinct cases to discuss, each of which depends upon the value and sign of the number a. • Case I: a < 0 If a < 0, then the graph of y = a is a horizontal line that lies strictly below the x-axis, as shown in Figure 2(a). In this case, the equation |x| = a has no solutions because the graphs of y = a and y = |x| do not intersect. 1 Copyrighted material. See: http://msenux.redwoods.edu/IntAlgText/ Version: Fall 2007 374 Chapter 4 Absolute Value Functions • Case II: a = 0 If a = 0, then the graph of y = 0 is a horizontal line that coincides with the x-axis, as shown in Figure 2(b). -

Absolute Values and Discrete Valuations
18.785 Number theory I Fall 2015 Lecture #1 09/10/2015 1 Absolute values and discrete valuations 1.1 Introduction At its core, number theory is the study of the ring Z and its fraction field Q. Many questions about Z and Q naturally lead one to consider finite extensions K=Q, known as number fields, and their rings of integers OK , which are finitely generated extensions of Z (the integral closure of Z in K, as we shall see). There is an analogous relationship between the ring Fq[t] of polynomials over a finite field Fq, its fraction field Fq(t), and the finite extensions of Fq(t), which are known as (global) function fields; these fields play an important role in arithmetic geometry, as they are are categorically equivalent to nice (smooth, projective, geometrically integral) curves over finite fields. Number fields and function fields are collectively known as global fields. Associated to each global field k is an infinite collection of local fields corresponding to the completions of k with respect to its absolute values; for the field of rational numbers Q, these are the field of real numbers R and the p-adic fields Qp (as you will prove on Problem Set 1). The ring Z is a principal ideal domain (PID), as is Fq[t]. These rings have dimension one, which means that every nonzero prime ideal is maximal; thus each nonzero prime ideal has an associated residue field, and for both Z and Fq[t] these residue fields are finite. In the case of Z we have residue fields Z=pZ ' Fp for each prime p, and for Fq[t] we have residue fields Fqd associated to each irreducible polynomial of degree d. -

An Introduction to the P-Adic Numbers Charles I
Union College Union | Digital Works Honors Theses Student Work 6-2011 An Introduction to the p-adic Numbers Charles I. Harrington Union College - Schenectady, NY Follow this and additional works at: https://digitalworks.union.edu/theses Part of the Logic and Foundations of Mathematics Commons Recommended Citation Harrington, Charles I., "An Introduction to the p-adic Numbers" (2011). Honors Theses. 992. https://digitalworks.union.edu/theses/992 This Open Access is brought to you for free and open access by the Student Work at Union | Digital Works. It has been accepted for inclusion in Honors Theses by an authorized administrator of Union | Digital Works. For more information, please contact [email protected]. AN INTRODUCTION TO THE p-adic NUMBERS By Charles Irving Harrington ********* Submitted in partial fulllment of the requirements for Honors in the Department of Mathematics UNION COLLEGE June, 2011 i Abstract HARRINGTON, CHARLES An Introduction to the p-adic Numbers. Department of Mathematics, June 2011. ADVISOR: DR. KARL ZIMMERMANN One way to construct the real numbers involves creating equivalence classes of Cauchy sequences of rational numbers with respect to the usual absolute value. But, with a dierent absolute value we construct a completely dierent set of numbers called the p-adic numbers, and denoted Qp. First, we take p an intuitive approach to discussing Qp by building the p-adic version of 7. Then, we take a more rigorous approach and introduce this unusual p-adic absolute value, j jp, on the rationals to the lay the foundations for rigor in Qp. Before starting the construction of Qp, we arrive at the surprising result that all triangles are isosceles under j jp. -

MAT 240 - Algebra I Fields Definition
MAT 240 - Algebra I Fields Definition. A field is a set F , containing at least two elements, on which two operations + and · (called addition and multiplication, respectively) are defined so that for each pair of elements x, y in F there are unique elements x + y and x · y (often written xy) in F for which the following conditions hold for all elements x, y, z in F : (i) x + y = y + x (commutativity of addition) (ii) (x + y) + z = x + (y + z) (associativity of addition) (iii) There is an element 0 ∈ F , called zero, such that x+0 = x. (existence of an additive identity) (iv) For each x, there is an element −x ∈ F such that x+(−x) = 0. (existence of additive inverses) (v) xy = yx (commutativity of multiplication) (vi) (x · y) · z = x · (y · z) (associativity of multiplication) (vii) (x + y) · z = x · z + y · z and x · (y + z) = x · y + x · z (distributivity) (viii) There is an element 1 ∈ F , such that 1 6= 0 and x·1 = x. (existence of a multiplicative identity) (ix) If x 6= 0, then there is an element x−1 ∈ F such that x · x−1 = 1. (existence of multiplicative inverses) Remark: The axioms (F1)–(F-5) listed in the appendix to Friedberg, Insel and Spence are the same as those above, but are listed in a different way. Axiom (F1) is (i) and (v), (F2) is (ii) and (vi), (F3) is (iii) and (vii), (F4) is (iv) and (ix), and (F5) is (vii). Proposition. Let F be a field. -

Physics from Archimedes to Rutherford
1 1 Physics from Archimedes to Rutherford 1.1 Mathematics and Physics in Antiquity In the 3rd millennium BC, the descendants of the Sumerians in Mesopotamia already used a sexagesimal (base 60) place-value numeral system of symbols to represent numbers, in which the position of a symbol determines its value. They also knew how to solve rhetorical algebraic equations (written in words, rather than symbols). By the 2nd millenium BC, Mesopotamians had com- piled tables of numbers representing the length of the sides of a right triangle.1 Their astronomers catalogued the motion of the stars and planets, as well as the occurrence of lunar eclipses. The day was divided into 24 hours, each hour into 60 minutes, each minute into 60 seconds. A decisive step in the development of mathematics was made by the Egyp- tians, who introduced special signs (hieratic numerals) for the numbers 1 to 9 and multiples of powers of 10. They devised methods of multiplication and division which only involved addition. However, their decimal number sys- tem did not include a zero symbol, nor did it use the principle of place value. The roots of modern science grew in the city-states of Ancient Greece scat- tered across the Eastern Mediterranean. The Greeks established physics as a science, greatly advanced astronomy, and made seminal contributions to mathematics, including the idea of formal mathematical proof, the basic rules of geometry, discoveries in number theory, and the rudiments of symbolic al- gebra and calculus. A remarkable testament to their ingenuity is the Antikythera mechanism, the oldest known complex scientific calculator, which was discovered in a wreck off the Greek island of Antikythera and is dated to about 100 BC (see Fig. -

What Are P-Adic Numbers?
Asia Pacific Mathematics Newsletter 1 WhatWhat are arep-Adic p-Adic Numbers? Numbers? What are What areThey They Used Used for? for? U A Rozikov U A Rozikov Abstract. In this short paper we give a popular intro- rational numbers, such that 2 < 1. This is done | |∗ duction to the theory of p-adic numbers. We give some as follows. Let Q be the field of rational numbers. properties of p-adic numbers distinguishing them to Every rational number x 0 can be represented “good” and “bad”. Some remarks about applications in the form x = pr n , where r, n Z, m is a positive of p-adic numbers to mathematics, biology and physics m ∈ are given. integer, ( p, n) = 1, ( p, m) = 1 and p is a fixed prime number. The p-adic absolute value (norm) of x is 1. p-Adic Numbers given by r p− , for x 0, p-adic numbers were introduced in 1904 by the x = | |p = German mathematician K Hensel. They are used 0, for x 0. intensively in number theory. p-adic analysis was The p-adic norm satisfies the so called strong developed (mainly for needs of number theory) triangle inequality in many directions, see, for example, [20, 50]. x + y max x , y , (2) When we write a number in decimal, we can | |p ≤ {| |p | |p} only have finitely many digits on the left of the and this is a non-Archimedean norm. decimal, but we can have infinitely many on the This definition of x has the effect that high | |p right of the decimal. -

OSTROWSKI for NUMBER FIELDS Ostrowski Classified the Nontrivial Absolute Values on Q: up to Equivalence, They Are the Usual (Arc
OSTROWSKI FOR NUMBER FIELDS KEITH CONRAD Ostrowski classified the nontrivial absolute values on Q: up to equivalence, they are the usual (archimedean) absolute value and the p-adic absolute values for different primes p, with none of these being equivalent to each other. We will see how this theorem extends to any number field K, giving a list of all the nontrivial absolute values on K up to equivalence. ordp(α) For a nonzero prime ideal p in OK and a constant c 2 (0; 1), the function jαj = c for α 2 K× (and j0j = 0) defines a nonarchimedean absolute value on K. We call this a p-adic absolute value. (Changing c produces an equivalent absolute value, so there is a well-defined p-adic topology on K, independent of c. This topology on OK amounts to declaring the k ideals p to be a neighborhood basis of 0 in OK .) For two different primes p and q, a p-adic absolute value and q-adic absolute value are inequivalent: the Chinese remainder theorem lets us find α 2 OK satisfying α ≡ 0 mod p and α ≡ 1 mod q, so the p-adic absolute value of α is less than 1 and the q-adic absolute value of α equals 1. Thus the two absolute values are inequivalent. Any embedding of K into R or C gives rise to an archimedean absolute value on K, with complex-conjugate embeddings yielding the same absolute value on K since ja + bij = ja − bij in C. Letting r1 be the number of real embedding of K and r2 be the number of pairs of complex-conjugate embeddings of K, there are r1 + 2r2 archimedean embeddings of K but only r1 + r2 archimedean absolute values (up to equivalence) since complex- conjugate embeddings define the same absolute value and the only way two archimedean embeddings define the same absolute value is when they come from a pair of complex- conjugate embeddings. -

4 Absolute Value Functions
4 Absolute Value Functions In this chapter we will introduce the absolute value function, one of the more useful functions that we will study in this course. Because it is closely related to the concept of distance, it is a favorite among statisticians, mathematicians, and other practitioners of science. Most readers probably already have an intuitive understanding of absolute value. You’ve probably seen that the absolute value of seven is seven, i.e., |7| = 7, and the absolute value of negative seven is also seven, i.e., | − 7| = 7. That is, the absolute value function takes a number as input, and then makes that number positive (if it isn’t already). Technically, because |0| = 0, which is not a positive number, we are forced to say that the absolute value function takes a number as input, and then makes it nonnegative (positive or zero). However, as you advance in your coursework, you will quickly discover that this intuitive notion of absolute value is insufficient when tackling more sophisticated prob- lems. In this chapter, as we try to raise our understanding of absolute value to a higher plane, we will encounter piecewise-defined functions and use them to create piecewise definitions for absolute value functions. These piecewise definitions will help us draw the graphs of a variety of absolute value functions. Finally we’ll conclude our work in this chapter by developing techniques for solving equations and inequalities containing expressions that implement the absolute value function. Table of Contents 4.1 Piecewise-Defined Functions . 335 Piecewise Constant Functions 336 Piecewise-Defined Functions 339 Exercises 347 Answers 350 4.2 Absolute Value . -

P-ADIC ABSOLUTE VALUES Contents 1. Introduction 1 2. P-Adic Absolute Value 2 3. Product Formula 4 4. Ultrametric Space 5 5. Topo
p-ADIC ABSOLUTE VALUES LOGAN QUICK Abstract. p-adic absolute values are functions which define magnitudes and distances on the rationals using the multiplicity of primes in the factorization of numbers. This paper will focus on the construction of p-adic absolute values, the new topology formed by these absolute values, and the proof of Ostrowski's theorem, which classifies all absolute values on Q. Contents 1. Introduction 1 2. p-adic Absolute Value 2 3. Product Formula 4 4. Ultrametric Space 5 5. Topology 6 6. Equivalent Absolute Values 8 7. Ostrowski's Theorem 8 Acknowledgments 10 References 10 1. Introduction Before we construct p-adic absolute values, we must understand what an absolute value is. So, we will begin by looking at the properties all absolute values share. k k Definition 1.1. Let be a field. An absolute value is a function |·| : ! R≥0. For all absolute values, the following properties hold: i) jxj ≥ 0 for all x 2 k. ii) jxj = 0 if and only if x = 0. iii) jxyj = jxjjyj, for all x; y 2 k. iv) jx + yj ≤ jxj + jyj, for all x; y 2 k. With these general properties, there are two absolute values which arise most easily. The first is the usual absolute value, which maps positive numbers to them- selves and negative numbers to their additive inverse: ( x if x ≥ 0; jxj1 = −x if x < 0: 1 2 LOGAN QUICK Secondly, there is the trivial absolute value which maps zero to zero and all other numbers to one: ( 1 if x 6= 0; jxj = 0 if x = 0: While these are the most natural absolute values to construct, far more can be constructed than just these two. -

Absolute Values and Completions
Absolute Values and Completions B.Sury This article is in the nature of a survey of the theory of complete fields. It is not exhaustive but serves the purpose of familiarising the readers with the basic notions involved. Hence, complete (!) proofs will not be given here. It is no surprise that algebraic number theory benefits a lot from introducing analysis therein. The familiar notion of construction of real numbers is just one aspect of this facility. § 1. Discrete valuations Definition 1.1. Let K be any field. A surjective map v : K∗ → Z is called a discrete valuation if: v(xy)= v(x)+ v(y), v(x + y) ≥ Inf(v(x), v(y)) Here, for notational purposes, one also defines v(0) = ∞. Note also that one must have v(1) = 0 = v(−1). Premier example 1.2. For each prime number or, more generally, for any non-zero prime ideal P in a Dedekind domain A, one has the P -adic valuation vP given by the prescription vP (x) = a where the fractional principal ideal (x)= P aI with I coprime to P . This is a discrete valuation on the quotient field K of A. Lemma 1.3. (a) If v is a discrete valuation on a field K, then Av := {x ∈ K : v(x) ≥ 0} is a local PID. Its maximal ideal is Pv = {x ∈ K : v(x) > 0}. ( Av is called the valuation ring of v). (b) For a discrete valuation v on a field K, if kv denotes the residue field i ∗ ∼ ∗ ∼ i i+1 ∼ Av/Pv and Ui = 1+Pv for i> 0, then Av/U1 = kv and Ui/Ui+1 = Pv/Pv = + kv .