DOCSLIB.ORG

What Are P-Adic Numbers?

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
What Are P-Adic Numbers? Asia Pacific Mathematics Newsletter 1 WhatWhat are arep-Adic p-Adic Numbers? Numbers? What are What areThey They Used Used for? for? U A Rozikov U A Rozikov Abstract. In this short paper we give a popular intro- rational numbers, such that 2 < 1. This is done | |∗ duction to the theory of p-adic numbers. We give some as follows. Let Q be the field of rational numbers. properties of p-adic numbers distinguishing them to Every rational number x 0 can be represented “good” and “bad”. Some remarks about applications in the form x = pr n , where r, n Z, m is a positive of p-adic numbers to mathematics, biology and physics m ∈ are given. integer, ( p, n) = 1, ( p, m) = 1 and p is a fixed prime number. The p-adic absolute value (norm) of x is 1. p-Adic Numbers given by r p− , for x 0, p-adic numbers were introduced in 1904 by the x = | |p = German mathematician K Hensel. They are used 0, for x 0. intensively in number theory. p-adic analysis was The p-adic norm satisfies the so called strong developed (mainly for needs of number theory) triangle inequality in many directions, see, for example, [20, 50]. x + y max x , y , (2) When we write a number in decimal, we can | |p ≤ {| |p | |p} only have finitely many digits on the left of the and this is a non-Archimedean norm. decimal, but we can have infinitely many on the This definition of x has the effect that high | |p right of the decimal. They might “terminate” (and powers of p become “small”, in particular 2n = | |2 become all zeros after some point) but they might 1/2n. By the fundamental theorem of arithmetic, not. The p-adic integers can be thought of as for a given non-zero rational number x there is a writing out integers in base p, but one can have unique finite set of distinct primes p1, ... , pr and infinitely many digits to the left of the decimal a corresponding sequence of non-zero integers ... = a1 ... ar (and none on the right; but the rational p-adic a1, , an such that x p1 pr . It then follows a numbers can have finitely many digits on the that x = p− i for all i = 1, ... , r, and x = 1 for | |pi i | |p right of the decimal). For example, the binary any other prime p p , ... , p . { 1 r} expansion of 35 is 1 20+1 21+0 22+0 23+0 24+1 25, For example, take 63/550 = 2 1 32 5 2 7 11 1 · · · · · · − · · − · · − often written in the shorthand notation 1000112. we have = = One has 1 0, 111111111 ...2 0, (1)2. But what is 2, if p = 2, = + ... 111111, 02 (1), 02? Compute (1), 02 1: 1/9, if p = 3, ... 111111, 0 2 25, if p = 5, +... 000001, 0 63 2 � � = ... � � 1/7, if p = 7, 000000, 02 �550�p � � Hence (1), 0 = 1. This equality can be written as 11, if p = 11, 2 − n 1 1, if p 13. − i n ≥ (1), 02 = lim 2 = lim (2 1) = 1. (1) n � n = − − →∞ i 0 →∞ We say that two norms 1 and 2 on Q are n � · � � · � This limit equivalent to limn 2 = 0. In real equivalent if there exists α > 0 such that →∞ n = case one has limn q 0 if and only if absolute α →∞ = 2. value q is less than 1. Remember that to define � · �1 � · � | | real numbers one considers all limit points of It is a theorem of Ostrowski (see [41]) that sequences of rational numbers, using the absolute each absolute value on Q is equivalent either value as metric. to the Euclidean absolute value , the trivial | · | To give a meaning of the limit (1), one has absolute value, or to one of the p-adic absolute to give a new absolute value , on the set of values for some prime p. So the only norms on | · |∗ October 2013, Volume 3 No 4 1 Asia Pacific Mathematics Newsletter 2 Q modulo equivalence are the absolute value, The sum ∞ n! exists in every Q . The follow- n=0 p the trivial absolute value and the p-adic absolute ing problem has been open since 1971. value which means that there are only as many Problem. Can ∞= n! be rational for some n 0 completions (with respect to a norm) of Q. prime p? The p-adic absolute value defines a metric It is not known if ∞ n! 0 in every Q . n=0 p x y p on Q. Two numbers x and y are p-adically 7. For any x Q, we have | − | ∈ closer as long as r is higher, such that pr divides = = x x p 1. x y p. Amazingly, for p 5 the result is that 135 | | | | | − | p:prime is closer to 10 than 35. The completion of Q with respect to p-adic This formula have been used to solve several norm defines the p-adic field which is denoted problems in number theory, many of them us- by Qp. Any p-adic number x 0 can be uniquely ing Helmut Hasse’s local-global principle, which represented in the canonical form roughly states that an equation can be solved over the rational numbers if and only if it can be x = pγ(x)(x + x p + x p2 + ), 0 1 2 ··· solved over the real numbers and over the p-adic where γ = γ(x) Z and x are integers, 0 x numbers for every prime p. ∈ j ≤ j ≤ p 1, x > 0, j = 0,1,2,... (see more detail [31, − 0 50, 54]). In this case x = p γ(x). The set of p-adic | |p − 3. “Bad” Properties of p-Adic Numbers numbers contains the field of rational numbers Q but is different from it. 1. Qp is not ordered. Using canonical form of p-adic numbers, simi- 2. Qp is not comparable with R, for example larly as real numbers, one makes arithmetic oper- √7 Q , but i = √ 1 Q . 5 − ∈ 5 ations on p-adic numbers (see for example, [41]). 3. Qp is not algebraically closed. But can be extended uniquely to the | · |p algebraic closure Qa and the completion of (Qa, ) 2. “Good” Properties of p-Adic Numbers p p |·|p is called Cp, the field of the p-adic complex num- The ultra-metric triangle inequality, i.e. (2), under- bers. Cp is no locally compact, but separable and lies many of the interesting differences between algebraically closed. real and p-adic analysis. The following properties Now define the functions expp (x) and logp (x). of p-adic numbers make some directions of the Given a Qp and r > 0 put p-adic analysis more simple than real analysis: ∈ B(a, r) = x Q : x a < r . 1. All triangles are isosceles. { ∈ p | − |p } 2. Any point of ball D(a, r) = x Q : x a r { ∈ p | − |p ≤ } The p-adic logarithm is defined by the series is center. Each ball has an empty boundary. Two n balls are either disjoint, or one is contained in the ∞ + (x 1) log (x) = log (1 + (x 1)) = ( 1)n 1 − , p p − − n other. n=1 3. if p p . This means that each | · |p1 | · |p2 1 2 which converges for x B(1, 1); prime number p generates its own field of p-adic ∈ The p-adic exponential is defined by numbers Qp. 4. x2 = 1 has a solution x Q if and only if ∞ xn − ∈ p exp (x) = , = p n! p 1 mod 4. n=0 Q 5. A sequence xn in p is a Cauchy sequence 1/(p 1) { } which converges for x B(0, p− − ). if and only if xn+1 xn p 0 as n . ∈ | − | → → ∞ Let x B(0, p 1/(p 1), then This has the useful corollary that a sum con- ∈ − − verges if and only if the individual terms tend to exp (x) =1, exp (x) 1 = x , log (1+x) = x , | p |p | p − |p | |p | p |p | |p zero: = + = + 6. (A student’s dream) ∞ a < if and only logp( expp(x)) x, expp( logp(1 x)) 1 x. n=1 n ∞ if a 0. n → 4. Some “good” functions become “bad”. For Since n! 0 we have, for example, | |p → example exp (x) is very “good” function on R, but ∞ ∞ as we seen above exp (x) is defined only on ball ( 1)nn!(n + 2) = 1, ( 1)nn!(n2 5) = 3. p − − − − 1/(p 1) n=0 n=0 B(0, p− − ). 2 October 2013, Volume 3 No 4 Asia Pacific Mathematics Newsletter3 4. Remarks about Applications p-adic mathematics in many directions: theory of distributions [6, 31], differential and pseudodif- When the p-adic numbers were introduced they ferential equations [32, 56], theory of probability considered as an exotic part of pure mathematics [31, 56] spectral theory of operators in a p-adic without any application (see for example [41, analogue of a Hilbert space [7, 8, 33]. 42, 50, 56] for applications of p-adic numbers The representation of p-adic numbers by se- to mathematics). Since p-adic numbers have the quences of digits gives a possibility to use this interesting property that they are said to be close number system for coding of information. There- when their difference is divisible by a high power fore p-adic models can be used for the description of p the higher the power the closer they are.
Load more

Recommended publications
  • OSTROWSKI for NUMBER FIELDS 1. Introduction in 1916, Ostrowski [6] Classified the Nontrivial Absolute Values on Q: up to Equival
    OSTROWSKI FOR NUMBER FIELDS KEITH CONRAD 1. Introduction In 1916, Ostrowski [6] classified the nontrivial absolute values on Q: up to equivalence, they are the usual (archimedean) absolute value and the p-adic absolute values for different primes p, with none of these being equivalent to each other. We will see how this theorem extends to a number field K, giving a list of all the nontrivial absolute values on K up to equivalence: for each nonzero prime ideal p in OK there is a p-adic absolute value, real embeddings of K and complex embeddings of K up to conjugation lead to archimedean absolute values on K, and every nontrivial absolute value on K is equivalent to a p-adic, real, or complex absolute value. 2. Defining nontrivial absolute values on K For each nonzero prime ideal p in OK , a p-adic absolute value on K is defined in terms × of a p-adic valuation ordp that is first defined on OK − f0g and extended to K by taking ratios. m Definition 2.1. For x 2 OK − f0g, define ordp(x) := m where xOK = p a with m ≥ 0 and p - a. We have ordp(xy) = ordp(x)+ordp(y) for nonzero x and y in OK by unique factorization of × ideals in OK . This lets us extend ordp to K by using ratios of nonzero numbers in OK : for × α 2 K , write α = x=y for nonzero x and y in OK and set ordp(α) := ordp(x) − ordp(y). To 0 0 0 0 0 0 see this is well-defined, if x=y = x =y for nonzero x; y; x , and y in OK then xy = x y 0 0 in OK , which implies ordp(x) + ordp(y ) = ordp(x ) + ordp(y), so ordp(x) − ordp(y) = 0 0 × × ordp(x ) − ordp(y ).
    [Show full text]
  • Proofs, Sets, Functions, and More: Fundamentals of Mathematical Reasoning, with Engaging Examples from Algebra, Number Theory, and Analysis
    Proofs, Sets, Functions, and More: Fundamentals of Mathematical Reasoning, with Engaging Examples from Algebra, Number Theory, and Analysis Mike Krebs James Pommersheim Anthony Shaheen FOR THE INSTRUCTOR TO READ i For the instructor to read We should put a section in the front of the book that organizes the organization of the book. It would be the instructor section that would have: { flow chart that shows which sections are prereqs for what sections. We can start making this now so we don't have to remember the flow later. { main organization and objects in each chapter { What a Cfu is and how to use it { Why we have the proofcomment formatting and what it is. { Applications sections and what they are { Other things that need to be pointed out. IDEA: Seperate each of the above into subsections that are labeled for ease of reading but not shown in the table of contents in the front of the book. ||||||||| main organization examples: ||||||| || In a course such as this, the student comes in contact with many abstract concepts, such as that of a set, a function, and an equivalence class of an equivalence relation. What is the best way to learn this material. We have come up with several rules that we want to follow in this book. Themes of the book: 1. The book has a few central mathematical objects that are used throughout the book. 2. Each central mathematical object from theme #1 must be a fundamental object in mathematics that appears in many areas of mathematics and its applications.
    [Show full text]
  • The Evolution of Numbers
    The Evolution of Numbers Counting Numbers Counting Numbers: {1, 2, 3, …} We use numbers to count: 1, 2, 3, 4, etc You can have "3 friends" A field can have "6 cows" Whole Numbers Whole numbers are the counting numbers plus zero. Whole Numbers: {0, 1, 2, 3, …} Negative Numbers We can count forward: 1, 2, 3, 4, ...... but what if we count backward: 3, 2, 1, 0, ... what happens next? The answer is: negative numbers: {…, -3, -2, -1} A negative number is any number less than zero. Integers If we include the negative numbers with the whole numbers, we have a new set of numbers that are called integers: {…, -3, -2, -1, 0, 1, 2, 3, …} The Integers include zero, the counting numbers, and the negative counting numbers, to make a list of numbers that stretch in either direction indefinitely. Rational Numbers A rational number is a number that can be written as a simple fraction (i.e. as a ratio). 2.5 is rational, because it can be written as the ratio 5/2 7 is rational, because it can be written as the ratio 7/1 0.333... (3 repeating) is also rational, because it can be written as the ratio 1/3 More formally we say: A rational number is a number that can be written in the form p/q where p and q are integers and q is not equal to zero. Example: If p is 3 and q is 2, then: p/q = 3/2 = 1.5 is a rational number Rational Numbers include: all integers all fractions Irrational Numbers An irrational number is a number that cannot be written as a simple fraction.
    [Show full text]
  • Control Number: FD-00133
    Math Released Set 2015 Algebra 1 PBA Item #13 Two Real Numbers Defined M44105 Prompt Rubric Task is worth a total of 3 points. M44105 Rubric Score Description 3 Student response includes the following 3 elements. • Reasoning component = 3 points o Correct identification of a as rational and b as irrational o Correct identification that the product is irrational o Correct reasoning used to determine rational and irrational numbers Sample Student Response: A rational number can be written as a ratio. In other words, a number that can be written as a simple fraction. a = 0.444444444444... can be written as 4 . Thus, a is a 9 rational number. All numbers that are not rational are considered irrational. An irrational number can be written as a decimal, but not as a fraction. b = 0.354355435554... cannot be written as a fraction, so it is irrational. The product of an irrational number and a nonzero rational number is always irrational, so the product of a and b is irrational. You can also see it is irrational with my calculations: 4 (.354355435554...)= .15749... 9 .15749... is irrational. 2 Student response includes 2 of the 3 elements. 1 Student response includes 1 of the 3 elements. 0 Student response is incorrect or irrelevant. Anchor Set A1 – A8 A1 Score Point 3 Annotations Anchor Paper 1 Score Point 3 This response receives full credit. The student includes each of the three required elements: • Correct identification of a as rational and b as irrational (The number represented by a is rational . The number represented by b would be irrational).
    [Show full text]
  • 1 Absolute Values and Valuations
    Algebra in positive Characteristic Fr¨uhjahrssemester 08 Lecturer: Prof. R. Pink Organizer: P. Hubschmid Absolute values, valuations and completion F. Crivelli ([email protected]) April 21, 2008 Introduction During this talk I’ll introduce the basic definitions and some results about valuations, absolute values of fields and completions. These notions will give two basic examples: the rational function field Fq(T ) and the field Qp of the p-adic numbers. 1 Absolute values and valuations All along this section, K denote a field. 1.1 Absolute values We begin with a well-known Definition 1. An absolute value of K is a function | | : K → R satisfying these properties, ∀ x, y ∈ K: 1. |x| = 0 ⇔ x = 0, 2. |x| ≥ 0, 3. |xy| = |x| |y|, 4. |x + y| ≤ |x| + |y|. (Triangle inequality) Note that if we set |x| = 1 for all 0 6= x ∈ K and |0| = 0, we have an absolute value on K, called the trivial absolute value. From now on, when we speak about an absolute value | |, we assume that | | is non-trivial. Moreover, if we define d : K × K → R by d(x, y) = |x − y|, x, y ∈ K, d is a metric on K and we have a topological structure on K. We have also some basic properties that we can deduce directly from the definition of an absolute value. 1 Lemma 1. Let | | be an absolute value on K. We have 1. |1| = 1, 2. |ζ| = 1, for all ζ ∈ K with ζd = 1 for some 0 6= d ∈ N (ζ is a root of unity), 3.
    [Show full text]
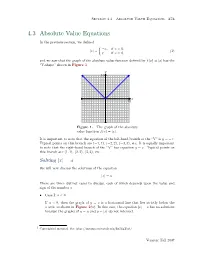
  • 4.3 Absolute Value Equations 373
    Section 4.3 Absolute Value Equations 373 4.3 Absolute Value Equations In the previous section, we defined −x, if x < 0. |x| = (1) x, if x ≥ 0, and we saw that the graph of the absolute value function defined by f(x) = |x| has the “V-shape” shown in Figure 1. y 10 x 10 Figure 1. The graph of the absolute value function f(x) = |x|. It is important to note that the equation of the left-hand branch of the “V” is y = −x. Typical points on this branch are (−1, 1), (−2, 2), (−3, 3), etc. It is equally important to note that the right-hand branch of the “V” has equation y = x. Typical points on this branch are (1, 1), (2, 2), (3, 3), etc. Solving |x| = a We will now discuss the solutions of the equation |x| = a. There are three distinct cases to discuss, each of which depends upon the value and sign of the number a. • Case I: a < 0 If a < 0, then the graph of y = a is a horizontal line that lies strictly below the x-axis, as shown in Figure 2(a). In this case, the equation |x| = a has no solutions because the graphs of y = a and y = |x| do not intersect. 1 Copyrighted material. See: http://msenux.redwoods.edu/IntAlgText/ Version: Fall 2007 374 Chapter 4 Absolute Value Functions • Case II: a = 0 If a = 0, then the graph of y = 0 is a horizontal line that coincides with the x-axis, as shown in Figure 2(b).
    [Show full text]
  • Absolute Values and Discrete Valuations
    18.785 Number theory I Fall 2015 Lecture #1 09/10/2015 1 Absolute values and discrete valuations 1.1 Introduction At its core, number theory is the study of the ring Z and its fraction field Q. Many questions about Z and Q naturally lead one to consider finite extensions K=Q, known as number fields, and their rings of integers OK , which are finitely generated extensions of Z (the integral closure of Z in K, as we shall see). There is an analogous relationship between the ring Fq[t] of polynomials over a finite field Fq, its fraction field Fq(t), and the finite extensions of Fq(t), which are known as (global) function fields; these fields play an important role in arithmetic geometry, as they are are categorically equivalent to nice (smooth, projective, geometrically integral) curves over finite fields. Number fields and function fields are collectively known as global fields. Associated to each global field k is an infinite collection of local fields corresponding to the completions of k with respect to its absolute values; for the field of rational numbers Q, these are the field of real numbers R and the p-adic fields Qp (as you will prove on Problem Set 1). The ring Z is a principal ideal domain (PID), as is Fq[t]. These rings have dimension one, which means that every nonzero prime ideal is maximal; thus each nonzero prime ideal has an associated residue field, and for both Z and Fq[t] these residue fields are finite. In the case of Z we have residue fields Z=pZ ' Fp for each prime p, and for Fq[t] we have residue fields Fqd associated to each irreducible polynomial of degree d.
    [Show full text]
  • E6-132-29.Pdf
    HISTORY OF MATHEMATICS – The Number Concept and Number Systems - John Stillwell THE NUMBER CONCEPT AND NUMBER SYSTEMS John Stillwell Department of Mathematics, University of San Francisco, U.S.A. School of Mathematical Sciences, Monash University Australia. Keywords: History of mathematics, number theory, foundations of mathematics, complex numbers, quaternions, octonions, geometry. Contents 1. Introduction 2. Arithmetic 3. Length and area 4. Algebra and geometry 5. Real numbers 6. Imaginary numbers 7. Geometry of complex numbers 8. Algebra of complex numbers 9. Quaternions 10. Geometry of quaternions 11. Octonions 12. Incidence geometry Glossary Bibliography Biographical Sketch Summary A survey of the number concept, from its prehistoric origins to its many applications in mathematics today. The emphasis is on how the number concept was expanded to meet the demands of arithmetic, geometry and algebra. 1. Introduction The first numbers we all meet are the positive integers 1, 2, 3, 4, … We use them for countingUNESCO – that is, for measuring the size– of collectionsEOLSS – and no doubt integers were first invented for that purpose. Counting seems to be a simple process, but it leads to more complex processes,SAMPLE such as addition (if CHAPTERSI have 19 sheep and you have 26 sheep, how many do we have altogether?) and multiplication ( if seven people each have 13 sheep, how many do they have altogether?). Addition leads in turn to the idea of subtraction, which raises questions that have no answers in the positive integers. For example, what is the result of subtracting 7 from 5? To answer such questions we introduce negative integers and thus make an extension of the system of positive integers.
    [Show full text]
  • An Introduction to the P-Adic Numbers Charles I
    Union College Union | Digital Works Honors Theses Student Work 6-2011 An Introduction to the p-adic Numbers Charles I. Harrington Union College - Schenectady, NY Follow this and additional works at: https://digitalworks.union.edu/theses Part of the Logic and Foundations of Mathematics Commons Recommended Citation Harrington, Charles I., "An Introduction to the p-adic Numbers" (2011). Honors Theses. 992. https://digitalworks.union.edu/theses/992 This Open Access is brought to you for free and open access by the Student Work at Union | Digital Works. It has been accepted for inclusion in Honors Theses by an authorized administrator of Union | Digital Works. For more information, please contact [email protected]. AN INTRODUCTION TO THE p-adic NUMBERS By Charles Irving Harrington ********* Submitted in partial fulllment of the requirements for Honors in the Department of Mathematics UNION COLLEGE June, 2011 i Abstract HARRINGTON, CHARLES An Introduction to the p-adic Numbers. Department of Mathematics, June 2011. ADVISOR: DR. KARL ZIMMERMANN One way to construct the real numbers involves creating equivalence classes of Cauchy sequences of rational numbers with respect to the usual absolute value. But, with a dierent absolute value we construct a completely dierent set of numbers called the p-adic numbers, and denoted Qp. First, we take p an intuitive approach to discussing Qp by building the p-adic version of 7. Then, we take a more rigorous approach and introduce this unusual p-adic absolute value, j jp, on the rationals to the lay the foundations for rigor in Qp. Before starting the construction of Qp, we arrive at the surprising result that all triangles are isosceles under j jp.
    [Show full text]
  • Chapter I, the Real and Complex Number Systems
    CHAPTER I THE REAL AND COMPLEX NUMBERS DEFINITION OF THE NUMBERS 1, i; AND p2 In order to make precise sense out of the concepts we study in mathematical analysis, we must first come to terms with what the \real numbers" are. Everything in mathematical analysis is based on these numbers, and their very definition and existence is quite deep. We will, in fact, not attempt to demonstrate (prove) the existence of the real numbers in the body of this text, but will content ourselves with a careful delineation of their properties, referring the interested reader to an appendix for the existence and uniqueness proofs. Although people may always have had an intuitive idea of what these real num- bers were, it was not until the nineteenth century that mathematically precise definitions were given. The history of how mathematicians came to realize the necessity for such precision in their definitions is fascinating from a philosophical point of view as much as from a mathematical one. However, we will not pursue the philosophical aspects of the subject in this book, but will be content to con- centrate our attention just on the mathematical facts. These precise definitions are quite complicated, but the powerful possibilities within mathematical analysis rely heavily on this precision, so we must pursue them. Toward our primary goals, we will in this chapter give definitions of the symbols (numbers) 1; i; and p2: − The main points of this chapter are the following: (1) The notions of least upper bound (supremum) and greatest lower bound (infimum) of a set of numbers, (2) The definition of the real numbers R; (3) the formula for the sum of a geometric progression (Theorem 1.9), (4) the Binomial Theorem (Theorem 1.10), and (5) the triangle inequality for complex numbers (Theorem 1.15).
    [Show full text]
  • Rational and Irrational Numbers 1
    CONCEPT DEVELOPMENT Mathematics Assessment Project CLASSROOM CHALLENGES A Formative Assessment Lesson Rational and Irrational Numbers 1 Mathematics Assessment Resource Service University of Nottingham & UC Berkeley Beta Version For more details, visit: http://map.mathshell.org © 2012 MARS, Shell Center, University of Nottingham May be reproduced, unmodified, for non-commercial purposes under the Creative Commons license detailed at http://creativecommons.org/licenses/by-nc-nd/3.0/ - all other rights reserved Rational and Irrational Numbers 1 MATHEMATICAL GOALS This lesson unit is intended to help you assess how well students are able to distinguish between rational and irrational numbers. In particular, it aims to help you identify and assist students who have difficulties in: • Classifying numbers as rational or irrational. • Moving between different representations of rational and irrational numbers. COMMON CORE STATE STANDARDS This lesson relates to the following Standards for Mathematical Content in the Common Core State Standards for Mathematics: N-RN: Use properties of rational and irrational numbers. This lesson also relates to the following Standards for Mathematical Practice in the Common Core State Standards for Mathematics: 3. Construct viable arguments and critique the reasoning of others. INTRODUCTION The lesson unit is structured in the following way: • Before the lesson, students attempt the assessment task individually. You then review students’ work and formulate questions that will help them improve their solutions. • The lesson is introduced in a whole-class discussion. Students then work collaboratively in pairs or threes to make a poster on which they classify numbers as rational and irrational. They work with another group to compare and check solutions.
    [Show full text]
  • [email protected] 2 Math480/540, TOPICS in MODERN MATH
    1 Department of Mathematics, The University of Pennsylvania, Philadel- phia, PA 19104-6395 E-mail address: [email protected] 2 Math480/540, TOPICS IN MODERN MATH. What are numbers? A.A.Kirillov Dec. 2007 2 The aim of this course is to show, what meaning has the notion of number in modern mathematics; tell about the problems arising in connection with different understanding of numbers and how these problems are being solved. Of course, I can explain only first steps of corresponding theories. For those who want to know more, I indicate the appropriate literature. 0.1 Preface The “muzhiks” near Vyatka lived badly. But they did not know it and believed that they live well, not worse than the others A.Krupin, “The live water.” When a school student first meet mathematics, (s)he is told that it is a science which studies numbers and figures. Later, in a college, (s)he learns analytic geometry which express geometric notions using numbers. So, it seems that numbers is the only object of study in mathematics. True, if you open a modern mathematical journal and try to read any article, it is very probable that you will see no numbers at all. Instead, au- thors speak about sets, functions, operators, groups, manifolds, categories, etc. Nevertheless, all these notions in one way or another are based on num- bers and the final result of any mathematical theory usually is expressed by a number. So, I think it is useful to discuss with math major students the ques- tion posed in the title.
    [Show full text]