DOCSLIB.ORG

String's Double Polarisation and Piano Source Identification

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
String's Double Polarisation and Piano Source Identification Piano acoustics : string’s double polarisation and piano source identification Jin Jack Tan To cite this version: Jin Jack Tan. Piano acoustics : string’s double polarisation and piano source identification. Acoustics [physics.class-ph]. Université Paris Saclay (COmUE), 2017. English. NNT : 2017SACLY014. tel- 01755039 HAL Id: tel-01755039 https://pastel.archives-ouvertes.fr/tel-01755039 Submitted on 30 Mar 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. NNT : 2017SACLY014 THÈSE DE DOCTORAT DE L’UNIVERSITÉ PARIS-SACLAY PRÉPARÉE ENSTA PARISTECH Ecole doctorale n◦579 L’école Doctorale Sciences Méchaniques et Énergétiques, Matériaux et Géosciences (SMEMaG) Spécialité de doctorat: Acoustique par M. JIN JACK TAN Piano acoustics: string’s double polarisation and piano source identification Thèse presentée et soutenue à Palaiseau le 30 Novembre 2017. Composition du Jury : M. FRANÇOIS GAUTIER Université du Maine (Rapporteur) M. XAVIER BOUTILLON CNRS (Rapporteur) M. BERTRAND DAVID Télécom ParisTech (Président) Mme. JULIETTE CHABASSIER INRIA (Examinatrice) M. KEREM EGE INSA de Lyon (Examinateur) M. CYRIL TOUZÉ ENSTA ParisTech (Directeur de thèse) M. BENJAMIN COTTÉ ENSTA ParisTech (Co-directeur de thèse) To my late uncle, Tan Cheng Kee, and my late aunt, Ch’ng Chin Nigh, both of whom have passed away during the final few months of my thesis preparation. Titre : Acoustique du piano : double polarisation de la corde et identification de sources Mots clefs : modele physique de piano, simulation numerique, corde, chevalet, identification de sources Résumé : L’objectif de cette thèse est d’améliorer la compréhension de l’acoustique du piano dans le contexte de la synthèse sonore par modèles physiques. Le manuscrit est décomposé en trois parties principales, dont les deux premières ont pour but la compréhension de l’origine de la double polarisation de la corde de piano, tandis que la dernière se focalise sur l’identification de sources d’un piano complet. Dans la première partie, la non linéarité géométrique, intervenant lorsque les amplitudes de vibration sont grandes, est étudiée afin de comprendre si le couplage non linéaire peut transmettre de l’énergie à une polarisa- tion non initialement excitée et mener ainsi au phénomène de double polarisation. Un développement en échelles multiples est mené sur un modèle de corde de Kirchhoff-Carrier avec les deux extrémités fixes, restreint au mode fondamental de chacune des polarisations. Les deux oscillateurs ont alors des fréquences très proches, on parle de résonance 1:1. La condition d’existence et le critère de stabilité pour l’apparition de double polarisation sont obtenus et validés numériquement sur la base des équations de Kirchhoff-Carrier, ainsi qu’avec un modèle de corde enrichi. Des expériences sont menées sur un dispositif monocorde où les angles de polarisation naturelle de la corde, le désaccord entre les deux polarisations et le comportement non linéaire son observés et identifiés. La seconde partie se concentre sur le couplage entre la corde et le chevalet. Les degrés de liberté de la corde sont couplés au chevalet dont les mouvements (translation/rotation) sont représentés par un ensemble d’oscillateurs. Les fréquences propres des différents systèmes couplés sont analysés. Des schémas numériques sont proposés et mis en œuvre pour une résolution directe. Ces schémas résolvent les équations de corde par une méthode d’éléments finis d’ordre élevé et les équations du chevalet analytiquement. Les conditions de cou- plage entre corde et chevalet sont assurées par des multiplicateurs de Lagrange. Expérimentalement, la corde est tendue sur le chevalet dans une configuration de type zig-zag et excitée verticalement ou horizontalement. Dans les deux cas, les phénomènes de double polarisation et de double décroissance sont observés et des résultats qualitativement similaires sont obtenus avec les modèles numériques. La dernière partie s’attache à décrire quantitativement les différentes sources vibro-acoustiques d’un pi- ano complet. Une étude est menée en utilisant une analyse des chemins de transfert (transfer path analysis en anglais) sur un piano Bösendorfer 280VC-9. Les contributions de la table d’harmonie, des parties interne et externe de la ceinture, du cadre en fonte et du couvercle sont étudiées dans le domaine fréquentiel. L’analyse montre que la table d’harmonie est le principal contributeur mais que le cadre en fonte et le couvercle jouent également un rôle significatif, en particulier à hautes fréquences. Title : Piano acoustics: string’s double polarisation and piano source identification Keywords : physical modelling of piano, numerical simulation, string, bridge, source identification Abstract : The objective of this thesis is to improve the understanding of the acoustics of the piano in the context of physically-based sound synthesis. The manuscript is decomposed in three parts, the first two being devoted to the understanding of the origin of the double polarisation in piano string, while the third one is dedicated to the identification of sound sources of a complete piano. In the first part, the geometric (large-amplitude) nonlinearity is studied in order to understand if the nonlin- ear coupling can transfer energy to an initially non excited polarisation, thus leading to the double polarisation phenomenon. A multiple-scale analysis is conducted on a Kirchhoff-Carrier string model with fixed boundary conditions at both ends. Each polarisation is restrained to its fundamental mode and thus presenting a 1:1 in- ternal resonance. The existence condition and stability criteria for double polarisation to occur are obtained and validated numerically based on the Kirchhoff-Carrier equations, as well as a more enriched geometrically exact string model. Experiments are carried out on a monochord setup where the natural polarisation angles of the string, detuning between the two polarisations and its nonlinear behaviour are observed and identified. The second part is devoted to the string/bridge coupling. The degrees of freedom of the string are coupled to the bridge whose translational and rotational motions are represented by a set of oscillators. The eigenfrequencies of various coupled systems are analysed. Numerical schemes are proposed and implemented where the string is solved via high-order finite-element method while the lumped bridge is solved analytically and coupled to the string by Lagrange multipliers. Experimentally, the string is strung over a bridge in a zig-zag configuration and excited vertically and horizontally. In both cases, double polarisation and double decay are observed and similar results are also obtained qualitatively in numerical models. The last part is devoted to a quantitative description of the vibroacoustic sources of a Bösendorfer 280VC-9 piano via operational transfer path analysis. The contribution of the soundboard, inner and outer rim, iron frame and lid are investigated in the frequency domain. It is found out that the soundboard is the primary contributor but the iron frame and the lid also play a significant role, especially at high frequencies. Université Paris-Saclay Espace Technologique / Immeuble Discovery Route de l’Orme aux Merisiers RD 128 / 91190 Saint-Aubin, France Acknowledgment This whole thesis would not have been possible without the generous sup- ports from the BATWOMAN Initial Training Network (ITN) (European Commission grant 605867). The BATWOMAN ITN is a Marie Skłodowska- Curie Actions project under the Framework Programme 7 (FP7) fund. I ex- press my utmost gratitude and appreciation for their supports. – see batwoman.eu for more information. I still remembered the night when I first received the email from Antoine Chaigne in March 2014 about my recruitment as a PhD candidate for the so-called "piano project". I was on my way to meet my girlfriend and she was the first person I broke the good news to. Upon reflection, perhaps she foresaw the difficulties of being apart for 3 years back then and broke down in tears. As of writing, I am one day away from fulfilling my contract with my thesis ready to submit and we are still together. These 3 years are simply monumental to me, for which I make a giant step for my career as well as in building my own family. All her dedications, commitment and sacrifices are deeply remembered and I am forever in her debt. Thank you, Sin Yong, for being the pillar despite being more than 10,000km away. Over these three years, I have been very lucky to be under the wings of Cyril Touzé, Benjamin Cotté, Patrick Joly and Antoine Chaigne. They are all incredible supervi- sors and have guided this lost deer to the right track numerously. It has been a wild ride with the final result obtained just weeks before the deadline (thanks Benjamin for showing me the important figure). If anyone thinks of being a student under them or wanting to collaborate on research, I would wholeheartedly recommend them without any hesitation. I have been glad to be part of an amazing Tan family who have been visiting me as often as they could and provide emotional supports whenever I need it despite the time difference and distance. I am sure they are also proud of my achievement. A special shout out to my sister in Manchester whom I visited and freeloaded every year during the Christmas break. In ENSTA, I am blessed to meet some great friends and colleagues. Honorable men- tion to the real Batwoman Àngels Aragonès who understands life as a foreigner in France. I am also fortunate to have met Tommy, Aurélien, Simon and Luca during different time of my stay in ENSTA.
Load more

Recommended publications
  • African Music Vol 6 No 2(Seb).Cdr
    94 JOURNAL OF INTERNATIONAL LIBRARY OF AFRICAN MUSIC THE GORA AND THE GRAND’ GOM-GOM: by ERICA MUGGLESTONE 1 INTRODUCTION For three centuries the interest of travellers and scholars alike has been aroused by the gora, an unbraced mouth-resonated musical bow peculiar to South Africa, because it is organologically unusual in that it is a blown chordophone.2 A split quill is attached to the bowstring at one end of the instrument. The string is passed through a hole in one end of the quill and secured; the other end of the quill is then bound or pegged to the stave. The string is lashed to the other end of the stave so that it may be tightened or loosened at will. The player holds the quill lightly bet­ ween his parted lips, and, by inhaling and exhaling forcefully, causes the quill (and with it the string) to vibrate. Of all the early descriptions of the gora, that of Peter Kolb,3 a German astronom­ er who resided at the Cape of Good Hope from 1705 to 1713, has been the most contentious. Not only did his character and his publication in general come under attack, but also his account of Khoikhoi4 musical bows in particular. Kolb’s text indicates that two types of musical bow were observed, to both of which he applied the name gom-gom. The use of the same name for both types of bow and the order in which these are described in the text, seems to imply that the second type is a variant of the first.
    [Show full text]
  • Lab 12. Vibrating Strings
    Lab 12. Vibrating Strings Goals • To experimentally determine the relationships between the fundamental resonant frequency of a vibrating string and its length, its mass per unit length, and the tension in the string. • To introduce a useful graphical method for testing whether the quantities x and y are related by a “simple power function” of the form y = axn. If so, the constants a and n can be determined from the graph. • To experimentally determine the relationship between resonant frequencies and higher order “mode” numbers. • To develop one general relationship/equation that relates the resonant frequency of a string to the four parameters: length, mass per unit length, tension, and mode number. Introduction Vibrating strings are part of our common experience. Which as you may have learned by now means that you have built up explanations in your subconscious about how they work, and that those explanations are sometimes self-contradictory, and rarely entirely correct. Musical instruments from all around the world employ vibrating strings to make musical sounds. Anyone who plays such an instrument knows that changing the tension in the string changes the pitch, which in physics terms means changing the resonant frequency of vibration. Similarly, changing the thickness (and thus the mass) of the string also affects its sound (frequency). String length must also have some effect, since a bass violin is much bigger than a normal violin and sounds much different. The interplay between these factors is explored in this laboratory experi- ment. You do not need to know physics to understand how instruments work. In fact, in the course of this lab alone you will engage with material which entire PhDs in music theory have been written.
    [Show full text]
  • The Science of String Instruments
    The Science of String Instruments Thomas D. Rossing Editor The Science of String Instruments Editor Thomas D. Rossing Stanford University Center for Computer Research in Music and Acoustics (CCRMA) Stanford, CA 94302-8180, USA [email protected] ISBN 978-1-4419-7109-8 e-ISBN 978-1-4419-7110-4 DOI 10.1007/978-1-4419-7110-4 Springer New York Dordrecht Heidelberg London # Springer Science+Business Media, LLC 2010 All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed on acid-free paper Springer is part of Springer ScienceþBusiness Media (www.springer.com) Contents 1 Introduction............................................................... 1 Thomas D. Rossing 2 Plucked Strings ........................................................... 11 Thomas D. Rossing 3 Guitars and Lutes ........................................................ 19 Thomas D. Rossing and Graham Caldersmith 4 Portuguese Guitar ........................................................ 47 Octavio Inacio 5 Banjo ...................................................................... 59 James Rae 6 Mandolin Family Instruments........................................... 77 David J. Cohen and Thomas D. Rossing 7 Psalteries and Zithers .................................................... 99 Andres Peekna and Thomas D.
    [Show full text]
  • Standing Waves and Sound
    Standing Waves and Sound Waves are vibrations (jiggles) that move through a material Frequency: how often a piece of material in the wave moves back and forth. Waves can be longitudinal (back-and- forth motion) or transverse (up-and- down motion). When a wave is caught in between walls, it will bounce back and forth to create a standing wave, but only if its frequency is just right! Sound is a longitudinal wave that moves through air and other materials. In a sound wave the molecules jiggle back and forth, getting closer together and further apart. Work with a partner! Take turns being the “wall” (hold end steady) and the slinky mover. Making Waves with a Slinky 1. Each of you should hold one end of the slinky. Stand far enough apart that the slinky is stretched. 2. Try making a transverse wave pulse by having one partner move a slinky end up and down while the other holds their end fixed. What happens to the wave pulse when it reaches the fixed end of the slinky? Does it return upside down or the same way up? Try moving the end up and down faster: Does the wave pulse get narrower or wider? Does the wave pulse reach the other partner noticeably faster? 3. Without moving further apart, pull the slinky tighter, so it is more stretched (scrunch up some of the slinky in your hand). Make a transverse wave pulse again. Does the wave pulse reach the end faster or slower if the slinky is more stretched? 4. Try making a longitudinal wave pulse by folding some of the slinky into your hand and then letting go.
    [Show full text]
  • Pedal in Liszt's Piano Music!
    ! Abstract! The purpose of this study is to discuss the problems that occur when some of Franz Liszt’s original pedal markings are realized on the modern piano. Both the construction and sound of the piano have developed since Liszt’s time. Some of Liszt’s curious long pedal indications produce an interesting sound effect on instruments built in his time. When these pedal markings are realized on modern pianos the sound is not as clear as on a Liszt-time piano and in some cases it is difficult to recognize all the tones in a passage that includes these pedal markings. The precondition of this study is the respectful following of the pedal indications as scored by the composer. Therefore, the study tries to find means of interpretation (excluding the more frequent change of the pedal), which would help to achieve a clearer sound with the !effects of the long pedal on a modern piano.! This study considers the factors that create the difference between the sound quality of Liszt-time and modern instruments. Single tones in different registers have been recorded on both pianos for that purpose. The sound signals from the two pianos have been presented in graphic form and an attempt has been made to pinpoint the dissimilarities. In addition, some examples of the long pedal desired by Liszt have been recorded and the sound signals of these examples have been analyzed. The study also deals with certain aspects of the impact of texture and register on the clarity of sound in the case of the long pedal.
    [Show full text]
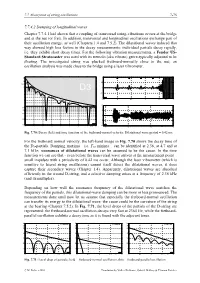
  • 7.7.4.2 Damping of Longitudinal Waves Chapter 7.7.4.1 Had Shown That a Coupling of Transversal String-Vibrations Occurs at the Bridge and at the Nut (Or Fret)
    7.7 Absorption of string oscillations 7-75 7.7.4.2 Damping of longitudinal waves Chapter 7.7.4.1 had shown that a coupling of transversal string-vibrations occurs at the bridge and at the nut (or fret). In addition, transversal and longitudinal oscillations exchange part of their oscillation energy, as well (Chapters 1.4 and 7.5.2). The dilatational waves induced that way showed high loss factors in the decay measurements: individual partials decay rapidly, i.e. they exhibit short decay times. For the following vibration measurements, a Fender US- Standard Stratocaster was used with its tremolo (aka vibrato) genre-typically adjusted to be floating. The investigated string was plucked fretboard-normally close to the nut; an oscillation analysis was made close to the bridge using a laser vibrometer. Fig. 7.70: Decay (left) and time function of the fretboard-normal velocity. Dilatational wave period = 0.42 ms. For the fretboard normal velocity, the left-hand image in Fig. 7.70 shows the decay time of the D3-partials. Damping maxima – i.e. T30 minima – can be identified at 2.36, at 4.7 and at 7.1 kHz; resonances of dilatational waves can be assumed to be the cause. In the time function we can see that - even before the transversal wave arrives at the measurement point – small impulses with a periodicity of 0.42 ms occur. Although the laser vibrometer (which is sensitive to lateral string oscillations) cannot itself detect the dilatational waves, it does capture their secondary waves (Chapter 1.4). Apparently, dilatational waves are absorbed efficiently in the wound D-string, and a selective damping arises at a frequency of 2.36 kHz (and its multiples).
    [Show full text]
  • Giant Slinky: Quantitative Exhibit Activity
    Name: _________________________________________________________________ Giant Slinky: Quantitative Exhibit Activity Materials: Tape Measure, Stopwatch, & Calculator. In this activity, we will explore wave properties using the Giant Slinky. Let’s start by describing the two types of waves: transverse and longitudinal. Transverse and Longitudinal Waves A transverse wave moves side-to-side orthogonal (at a right angle; perpendicular) to the direction the wave is moving. These waves can be created on the Slinky by shaking the end of it left and right. A longitudinal wave is a pressure wave alternating between high and low pressure. These waves can be created on the Slinky by gathering a few (about 5 or so) Slinky rings, compressing them with your hands and letting go. The area of high pressure is where the Slinky rings are bunched up and the area of low pressure is where the Slinky rings are spread apart. Transverse Waves Before we can do any math with our Slinky, we need to know a little more about its properties. Begin by measuring the length (L) of the Slinky (attachment disk to attachment disk). If your tape measure only measures in feet and inches, convert feet into meters using 1 ft = 0.3048 m. Length of Slinky: L = __________________m We must also know how long it takes a wave to travel the length of the Slinky so that we can calculate the speed of a wave. For now, we are going to investigate transverse waves, so make a single pulse by jerking the Slinky sharply to the left and right ONCE (very quickly) and then return the Slinky to the original center position.
    [Show full text]
  • Woods for Wooden Musical Instruments S
    ISMA 2014, Le Mans, France Woods for Wooden Musical Instruments S. Yoshikawaa and C. Walthamb aKyushu University, Graduate School of Design, 4-9-1 Shiobaru, Minami-ku, 815-8540 Fukuoka, Japan bUniversity of British Columbia, Dept of Physics & Astronomy, 6224 Agricultural Road, Vancouver, BC, Canada V6T 1Z1 [email protected] 281 ISMA 2014, Le Mans, France In spite of recent advances in materials science, wood remains the preferred construction material for musical instruments worldwide. Some distinguishing features of woods (light weight, intermediate quality factor, etc.) are easily noticed if we compare material properties between woods, a plastic (acrylic), and a metal (aluminum). Woods common in musical instruments (strings, woodwinds, and percussions) are typically (with notable exceptions) softwoods (e.g. Sitka spruce) as tone woods for soundboards, hardwoods (e.g. amboyna) as frame woods for backboards, and monocots (e.g. bamboo) as bore woods for woodwind bodies. Moreover, if we consider the radiation characteristics of tap tones from sample plates of Sitka spruce, maple, and aluminum, a large difference is observed above around 2 kHz that is attributed to the relative strength of shear and bending deformations in flexural vibrations. This shear effect causes an appreciable increase in the loss factor at higher frequencies. The stronger shear effect in Sitka spruce than in maple and aluminum seems to be relevant to soundboards because its low-pass filter effect with a cutoff frequency of about 2 kHz tends to lend the radiated sound a desired softness. A classification diagram of traditional woods based on an anti-vibration parameter (density ρ/sound speed c) and transmission parameter cQ is proposed.
    [Show full text]
  • Model-Based Digital Pianos: from Physics to Sound Synthesis Balazs Bank, Juliette Chabassier
    Model-based digital pianos: from physics to sound synthesis Balazs Bank, Juliette Chabassier To cite this version: Balazs Bank, Juliette Chabassier. Model-based digital pianos: from physics to sound synthesis. IEEE Signal Processing Magazine, Institute of Electrical and Electronics Engineers, 2018, 36 (1), pp.11. 10.1109/MSP.2018.2872349. hal-01894219 HAL Id: hal-01894219 https://hal.inria.fr/hal-01894219 Submitted on 12 Oct 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Model-based digital pianos: from physics to sound synthesis Bal´azsBank, Member, IEEE and Juliette Chabassier∗yz October 12, 2018 Abstract Piano is arguably one of the most important instruments in Western music due to its complexity and versatility. The size, weight, and price of grand pianos, and the relatively simple control surface (keyboard) have lead to the development of digital counterparts aiming to mimic the sound of the acoustic piano as closely as possible. While most commercial digital pianos are based on sample playback, it is also possible to reproduce the sound of the piano by modeling the physics of the instrument. The pro- cess of physical modeling starts with first understanding the physical principles, then creating accurate numerical models, and finally finding numerically optimized signal processing models that allow sound synthesis in real time by neglecting inaudible phe- nomena, and adding some perceptually important features by signal processing tricks.
    [Show full text]
  • The Musical Kinetic Shape: a Variable Tension String Instrument
    The Musical Kinetic Shape: AVariableTensionStringInstrument Ismet Handˇzi´c, Kyle B. Reed University of South Florida, Department of Mechanical Engineering, Tampa, Florida Abstract In this article we present a novel variable tension string instrument which relies on a kinetic shape to actively alter the tension of a fixed length taut string. We derived a mathematical model that relates the two-dimensional kinetic shape equation to the string’s physical and dynamic parameters. With this model we designed and constructed an automated instrument that is able to play frequencies within predicted and recognizable frequencies. This prototype instrument is also able to play programmed melodies. Keywords: musical instrument, variable tension, kinetic shape, string vibration 1. Introduction It is possible to vary the fundamental natural oscillation frequency of a taut and uniform string by either changing the string’s length, linear density, or tension. Most string musical instruments produce di↵erent tones by either altering string length (fretting) or playing preset and di↵erent string gages and string tensions. Although tension can be used to adjust the frequency of a string, it is typically only used in this way for fine tuning the preset tension needed to generate a specific note frequency. In this article, we present a novel string instrument concept that is able to continuously change the fundamental oscillation frequency of a plucked (or bowed) string by altering string tension in a controlled and predicted Email addresses: [email protected] (Ismet Handˇzi´c), [email protected] (Kyle B. Reed) URL: http://reedlab.eng.usf.edu/ () Preprint submitted to Applied Acoustics April 19, 2014 Figure 1: The musical kinetic shape variable tension string instrument prototype.
    [Show full text]
  • Numerical Simulations of Piano Strings. I. a Physical Model for A
    Numerical simulations of piano strings. I. A physical model for a struck string using finite difference methods AntoineChaigne SignalDepartment, CNRS UIL4 820, TelecomParis, 46 rue Barrault, 75634Paris Cedex13, France Anders Askenfelt Departmentof SpeechCommunication and Music Acoustics;Royal Institute of Technology(KTH), P.O. Box 700 14, S-100 44 Stockholm, Sweden (Received 8 March 1993;accepted for publication26 October 1993) The first attempt to generatemusical sounds by solvingthe equationsof vibratingstrings by meansof finitedifference methods (FDM) wasmade by Hiller and Ruiz [J. Audio Eng. Soc.19, 462472 (1971)]. It is shownhere how this numericalapproach and the underlyingphysical modelcan be improvedin order to simulatethe motion of the piano stringwith a high degree of realism.Starting from the fundamentalequations of a damped,stiff stringinteracting with a nonlinear hammer, a numerical finite differencescheme is derived, from which the time histories of stringdisplacement and velocityfor eachpoint of the stringare computedin the timedomain. The interactingforce between hammer and string,as well as the forceacting on the bridge,are givenby the samescheme. The performanceof the model is illustratedby a few examplesof simulated string waveforms. A brief discussionof the aspectsof numerical stability and dispersionwith referenceto the properchoice of samplingparameters is alsoincluded. PACS numbers: 43.75.Mn LIST OF SYMBOLS N numberof stringsegments coefficientsin the discretewave equation p stiffnessnonlinear exponent all(t) hammer
    [Show full text]
  • A Comparison of Viola Strings with Harmonic Frequency Analysis
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Student Research, Creative Activity, and Performance - School of Music Music, School of 5-2011 A Comparison of Viola Strings with Harmonic Frequency Analysis Jonathan Paul Crosmer University of Nebraska-Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/musicstudent Part of the Music Commons Crosmer, Jonathan Paul, "A Comparison of Viola Strings with Harmonic Frequency Analysis" (2011). Student Research, Creative Activity, and Performance - School of Music. 33. https://digitalcommons.unl.edu/musicstudent/33 This Article is brought to you for free and open access by the Music, School of at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Student Research, Creative Activity, and Performance - School of Music by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. A COMPARISON OF VIOLA STRINGS WITH HARMONIC FREQUENCY ANALYSIS by Jonathan P. Crosmer A DOCTORAL DOCUMENT Presented to the Faculty of The Graduate College at the University of Nebraska In Partial Fulfillment of Requirements For the Degree of Doctor of Musical Arts Major: Music Under the Supervision of Professor Clark E. Potter Lincoln, Nebraska May, 2011 A COMPARISON OF VIOLA STRINGS WITH HARMONIC FREQUENCY ANALYSIS Jonathan P. Crosmer, D.M.A. University of Nebraska, 2011 Adviser: Clark E. Potter Many brands of viola strings are available today. Different materials used result in varying timbres. This study compares 12 popular brands of strings. Each set of strings was tested and recorded on four violas. We allowed two weeks after installation for each string set to settle, and we were careful to control as many factors as possible in the recording process.
    [Show full text]