Kernel Density Estimator
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Deep Kernel Learning
Deep Kernel Learning Andrew Gordon Wilson∗ Zhiting Hu∗ Ruslan Salakhutdinov Eric P. Xing CMU CMU University of Toronto CMU Abstract (1996), who had shown that Bayesian neural net- works with infinitely many hidden units converged to Gaussian processes with a particular kernel (co- We introduce scalable deep kernels, which variance) function. Gaussian processes were subse- combine the structural properties of deep quently viewed as flexible and interpretable alterna- learning architectures with the non- tives to neural networks, with straightforward learn- parametric flexibility of kernel methods. ing procedures. Where neural networks used finitely Specifically, we transform the inputs of a many highly adaptive basis functions, Gaussian pro- spectral mixture base kernel with a deep cesses typically used infinitely many fixed basis func- architecture, using local kernel interpolation, tions. As argued by MacKay (1998), Hinton et al. inducing points, and structure exploit- (2006), and Bengio (2009), neural networks could ing (Kronecker and Toeplitz) algebra for automatically discover meaningful representations in a scalable kernel representation. These high-dimensional data by learning multiple layers of closed-form kernels can be used as drop-in highly adaptive basis functions. By contrast, Gaus- replacements for standard kernels, with ben- sian processes with popular kernel functions were used efits in expressive power and scalability. We typically as simple smoothing devices. jointly learn the properties of these kernels through the marginal likelihood of a Gaus- Recent approaches (e.g., Yang et al., 2015; Lloyd et al., sian process. Inference and learning cost 2014; Wilson, 2014; Wilson and Adams, 2013) have (n) for n training points, and predictions demonstrated that one can develop more expressive costO (1) per test point. -

Kernel Methods As Before We Assume a Space X of Objects and a Feature Map Φ : X → RD
Kernel Methods As before we assume a space X of objects and a feature map Φ : X → RD. We also assume training data hx1, y1i,... hxN , yN i and we define the data matrix Φ by defining Φt,i to be Φi(xt). In this section we assume L2 regularization and consider only training algorithms of the following form. N ∗ X 1 2 w = argmin Lt(w) + λ||w|| (1) w 2 t=1 Lt(w) = L(yt, w · Φ(xt)) (2) We have written Lt = L(yt, w · Φ) rather then L(mt(w)) because we now want to allow the case of regression where we have y ∈ R as well as classification where we have y ∈ {−1, 1}. Here we are interested in methods for solving (1) for D >> N. An example of D >> N would be a database of one thousand emails where for each email xt we have that Φ(xt) has a feature for each word of English so that D is roughly 100 thousand. We are interested in the case where inner products of the form K(x, y) = Φ(x)·Φ(y) can be computed efficiently independently of the size of D. This is indeed the case for email messages with feature vectors with a feature for each word of English. 1 The Kernel Method We can reduce ||w|| while holding L(yt, w · Φ(xt)) constant (for all t) by remov- ing any the component of w orthoganal to all vectors Φ(xt). Without loss of ∗ generality we can therefore assume that w is in the span of the vectors Φ(xt). -

3.2 the Periodogram
3.2 The periodogram The periodogram of a time series of length n with sampling interval ∆is defined as 2 ∆ n In(⌫)= (Xt X)exp( i2⇡⌫t∆) . n − − t=1 X In words, we compute the absolute value squared of the Fourier transform of the sample, that is we consider the squared amplitude and ignore the phase. Note that In is periodic with period 1/∆andthatIn(0) = 0 because we have centered the observations at the mean. The centering has no e↵ect for Fourier frequencies ⌫ = k/(n∆), k =0. 6 By mutliplying out the absolute value squared on the right, we obtain n n n 1 ∆ − I (⌫)= (X X)(X X)exp( i2⇡⌫(t s)∆)=∆ γ(h)exp( i2⇡⌫h). n n t − s − − − − t=1 s=1 h= n+1 X X X− Hence the periodogram is nothing else than the Fourier transform of the estimatedb acf. In the following, we assume that ∆= 1 in order to simplify the formula (although for applications the value of ∆in the original time scale matters for the interpretation of frequencies). By the above result, the periodogram seems to be the natural estimator of the spectral density 1 s(⌫)= γ(h)exp( i2⇡⌫h). − h= X1 However, a closer inspection shows that the periodogram has two serious shortcomings: It has large random fluctuations, and also a bias which can be large. We first consider the bias. Using the spectral representation, we see that up to a term which involves E(X ) X t − 2 1 n 2 i2⇡(⌫ ⌫0)t i⇡(n+1)(⌫ ⌫0) In(⌫)= e− − Z(d⌫0) = n e− − Dn(⌫ ⌫0)Z(d⌫0) . -

Lecture 2: Density Estimation 2.1 Histogram
STAT 535: Statistical Machine Learning Autumn 2019 Lecture 2: Density Estimation Instructor: Yen-Chi Chen Main reference: Section 6 of All of Nonparametric Statistics by Larry Wasserman. A book about the methodologies of density estimation: Multivariate Density Estimation: theory, practice, and visualization by David Scott. A more theoretical book (highly recommend if you want to learn more about the theory): Introduction to Nonparametric Estimation by A.B. Tsybakov. Density estimation is the problem of reconstructing the probability density function using a set of given data points. Namely, we observe X1; ··· ;Xn and we want to recover the underlying probability density function generating our dataset. 2.1 Histogram If the goal is to estimate the PDF, then this problem is called density estimation, which is a central topic in statistical research. Here we will focus on the perhaps simplest approach: histogram. For simplicity, we assume that Xi 2 [0; 1] so p(x) is non-zero only within [0; 1]. We also assume that p(x) is smooth and jp0(x)j ≤ L for all x (i.e. the derivative is bounded). The histogram is to partition the set [0; 1] (this region, the region with non-zero density, is called the support of a density function) into several bins and using the count of the bin as a density estimate. When we have M bins, this yields a partition: 1 1 2 M − 2 M − 1 M − 1 B = 0; ;B = ; ; ··· ;B = ; ;B = ; 1 : 1 M 2 M M M−1 M M M M In such case, then for a given point x 2 B`, the density estimator from the histogram will be n number of observations within B` 1 M X p (x) = × = I(X 2 B ): bM n length of the bin n i ` i=1 The intuition of this density estimator is that the histogram assign equal density value to every points within 1 Pn the bin. -

Density Estimation 36-708
Density Estimation 36-708 1 Introduction Let X1;:::;Xn be a sample from a distribution P with density p. The goal of nonparametric density estimation is to estimate p with as few assumptions about p as possible. We denote the estimator by pb. The estimator will depend on a smoothing parameter h and choosing h carefully is crucial. To emphasize the dependence on h we sometimes write pbh. Density estimation used for: regression, classification, clustering and unsupervised predic- tion. For example, if pb(x; y) is an estimate of p(x; y) then we get the following estimate of the regression function: Z mb (x) = ypb(yjx)dy where pb(yjx) = pb(y; x)=pb(x). For classification, recall that the Bayes rule is h(x) = I(p1(x)π1 > p0(x)π0) where π1 = P(Y = 1), π0 = P(Y = 0), p1(x) = p(xjy = 1) and p0(x) = p(xjy = 0). Inserting sample estimates of π1 and π0, and density estimates for p1 and p0 yields an estimate of the Bayes rule. For clustering, we look for the high density regions, based on an estimate of the density. Many classifiers that you are familiar with can be re-expressed this way. Unsupervised prediction is discussed in Section 9. In this case we want to predict Xn+1 from X1;:::;Xn. Example 1 (Bart Simpson) The top left plot in Figure 1 shows the density 4 1 1 X p(x) = φ(x; 0; 1) + φ(x;(j=2) − 1; 1=10) (1) 2 10 j=0 where φ(x; µ, σ) denotes a Normal density with mean µ and standard deviation σ. -

Consistent Kernel Mean Estimation for Functions of Random Variables
Consistent Kernel Mean Estimation for Functions of Random Variables , Carl-Johann Simon-Gabriel⇤, Adam Scibior´ ⇤ †, Ilya Tolstikhin, Bernhard Schölkopf Department of Empirical Inference, Max Planck Institute for Intelligent Systems Spemanstraße 38, 72076 Tübingen, Germany ⇤ joint first authors; † also with: Engineering Department, Cambridge University cjsimon@, adam.scibior@, ilya@, [email protected] Abstract We provide a theoretical foundation for non-parametric estimation of functions of random variables using kernel mean embeddings. We show that for any continuous function f, consistent estimators of the mean embedding of a random variable X lead to consistent estimators of the mean embedding of f(X). For Matérn kernels and sufficiently smooth functions we also provide rates of convergence. Our results extend to functions of multiple random variables. If the variables are dependent, we require an estimator of the mean embedding of their joint distribution as a starting point; if they are independent, it is sufficient to have separate estimators of the mean embeddings of their marginal distributions. In either case, our results cover both mean embeddings based on i.i.d. samples as well as “reduced set” expansions in terms of dependent expansion points. The latter serves as a justification for using such expansions to limit memory resources when applying the approach as a basis for probabilistic programming. 1 Introduction A common task in probabilistic modelling is to compute the distribution of f(X), given a measurable function f and a random variable X. In fact, the earliest instances of this problem date back at least to Poisson (1837). Sometimes this can be done analytically. -

Density and Distribution Estimation
Density and Distribution Estimation Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 04-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Density and Distribution Estimation Updated 04-Jan-2017 : Slide 1 Copyright Copyright c 2017 by Nathaniel E. Helwig Nathaniel E. Helwig (U of Minnesota) Density and Distribution Estimation Updated 04-Jan-2017 : Slide 2 Outline of Notes 1) PDFs and CDFs 3) Histogram Estimates Overview Overview Estimation problem Bins & breaks 2) Empirical CDFs 4) Kernel Density Estimation Overview KDE basics Examples Bandwidth selection Nathaniel E. Helwig (U of Minnesota) Density and Distribution Estimation Updated 04-Jan-2017 : Slide 3 PDFs and CDFs PDFs and CDFs Nathaniel E. Helwig (U of Minnesota) Density and Distribution Estimation Updated 04-Jan-2017 : Slide 4 PDFs and CDFs Overview Density Functions Suppose we have some variable X ∼ f (x) where f (x) is the probability density function (pdf) of X. Note that we have two requirements on f (x): f (x) ≥ 0 for all x 2 X , where X is the domain of X R X f (x)dx = 1 Example: normal distribution pdf has the form 2 1 − (x−µ) f (x) = p e 2σ2 σ 2π + which is well-defined for all x; µ 2 R and σ 2 R . Nathaniel E. Helwig (U of Minnesota) Density and Distribution Estimation Updated 04-Jan-2017 : Slide 5 PDFs and CDFs Overview Standard Normal Distribution If X ∼ N(0; 1), then X follows a standard normal distribution: 1 2 f (x) = p e−x =2 (1) 2π 0.4 ) x ( 0.2 f 0.0 −4 −2 0 2 4 x Nathaniel E. -

Recurrent Kernel Networks
Recurrent Kernel Networks Dexiong Chen Laurent Jacob Inria∗ CNRSy [email protected] [email protected] Julien Mairal Inria∗ [email protected] Abstract Substring kernels are classical tools for representing biological sequences or text. However, when large amounts of annotated data are available, models that allow end-to-end training such as neural networks are often preferred. Links between recurrent neural networks (RNNs) and substring kernels have recently been drawn, by formally showing that RNNs with specific activation functions were points in a reproducing kernel Hilbert space (RKHS). In this paper, we revisit this link by generalizing convolutional kernel networks—originally related to a relaxation of the mismatch kernel—to model gaps in sequences. It results in a new type of recurrent neural network which can be trained end-to-end with backpropagation, or without supervision by using kernel approximation techniques. We experimentally show that our approach is well suited to biological sequences, where it outperforms existing methods for protein classification tasks. 1 Introduction Learning from biological sequences is important for a variety of scientific fields such as evolution [8] or human health [16]. In order to use classical statistical models, a first step is often to map sequences to vectors of fixed size, while retaining relevant features for the considered learning task. For a long time, such features have been extracted from sequence alignment, either against a reference or between each others [3]. The resulting features are appropriate for sequences that are similar enough, but they become ill-defined when sequences are not suited to alignment. -
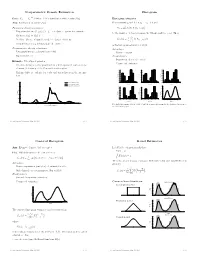
Nonparametric Density Estimation Histogram
Nonparametric Density Estimation Histogram iid Data: X1; : : : ; Xn » P where P is a distribution with density f(x). Histogram estimator Aim: Estimation of density f(x) For constants a0 and h, let ak = a0 + k h and Parametric density estimation: Hk = # Xi Xi 2 (ak¡1; ak] © ¯ ª ± Fit parametric model ff(xj)j 2 £g to data à parameter estimate ^ ¯ be the number of observations in the kth interval (ak¡1; ak]. Then ^ ± Estimate f(x) by f(xj) n ^ 1 f (x) = Hk 1 k¡ k (x) ± Problem: Choice of suitable model à danger of mis¯ts hist hn (a 1;a ] kP=1 ± Complex models (eg mixtures) are di±cult to ¯t is the histogram estimator of f(x). Nonparametric density estimation: Advantages: ± Few assumptions (eg density is smooth) ± Easy to compute ± Exploratory tool Disadvantages: ± Sensitive in choice of o®set a Example: Velocities of galaxies 0 ± Nonsmooth estimator ± Velocities in km/sec of 82 galaxies from 6 well-separated conic sections of an un¯lled survey of the Corona Borealis region. 0.54 0.5 0.56 0.45 0.48 0.4 ± Multimodality is evidence for voids and superclusters in the far uni- 0.40 0.36 0.3 0.32 verse. 0.27 0.24 Density Density 0.2 Density 0.18 0.16 0.1 0.09 0.08 0.00 0.0 0.00 0.25 Kernel estimate (h=0.814) 1 2 3 4 5 6 0.9 1.9 2.9 3.9 4.9 5.9 0.8 1.8 2.8 3.8 4.8 5.8 Kernel estimate (h=0.642) Duration Duration Duration Normal mixture model (k=4) 0.5 0.20 0.56 0.56 0.48 0.48 0.4 0.15 0.40 0.40 0.3 0.32 0.32 Density Density 0.24 Density 0.24 Density 0.2 0.10 0.16 0.16 0.1 0.08 0.08 0.05 0.00 0.00 0.0 0.7 1.7 2.7 3.7 4.7 5.7 0.6 1.6 2.6 3.6 4.6 5.6 1 2 3 4 5 Duration Duration Duration 0.00 0 10 20 30 40 Five shifted histograms with bin width 0.5 and the averaged histogram, for the duration of eruptions of Velocity of galaxy (1000km/s) the Old Faithful geyser. -

APPLIED SMOOTHING TECHNIQUES Part 1: Kernel Density Estimation
APPLIED SMOOTHING TECHNIQUES Part 1: Kernel Density Estimation Walter Zucchini October 2003 Contents 1 Density Estimation 2 1.1 Introduction . 2 1.1.1 The probability density function . 2 1.1.2 Non–parametric estimation of f(x) — histograms . 3 1.2 Kernel density estimation . 3 1.2.1 Weighting functions . 3 1.2.2 Kernels . 7 1.2.3 Densities with bounded support . 8 1.3 Properties of kernel estimators . 12 1.3.1 Quantifying the accuracy of kernel estimators . 12 1.3.2 The bias, variance and mean squared error of fˆ(x) . 12 1.3.3 Optimal bandwidth . 15 1.3.4 Optimal kernels . 15 1.4 Selection of the bandwidth . 16 1.4.1 Subjective selection . 16 1.4.2 Selection with reference to some given distribution . 16 1.4.3 Cross–validation . 18 1.4.4 ”Plug–in” estimator . 19 1.4.5 Summary and extensions . 19 1 Chapter 1 Density Estimation 1.1 Introduction 1.1.1 The probability density function The probability distribution of a continuous–valued random variable X is conventionally described in terms of its probability density function (pdf), f(x), from which probabilities associated with X can be determined using the relationship Z b P (a · X · b) = f(x)dx : a The objective of many investigations is to estimate f(x) from a sample of observations x1; x2; :::; xn . In what follows we will assume that the observations can be regarded as independent realizations of X. The parametric approach for estimating f(x) is to assume that f(x) is a member of some parametric family of distributions, e.g. -

Regression Discontinuity Design
Regression Discontinuity Design Marcelo Coca Perraillon University of Chicago May 13 & 18, 2015 An updated version including nonparametric estimation and code is available here: https://clas.ucdenver.edu/marcelo-perraillon/teaching/health-services- research-methods-i-hsmp-7607 © Marcelo Coca Perraillon, 2021. Please read the entire copyright notice using the link above. 1 / 51 Introduction Plan Overview of RDD Meaning and validity of RDD Several examples from the literature Estimation (where most decisions are made) Discussion of Almond et al (low birth weight) Stata code and data for all examples will be available on Chalk. Email me if you have questions: [email protected] 2 / 51 Introduction Basics Method developed to estimate treatment effects in non-experimental settings Provides causal estimates of treatment effects Good internal validity; some assumptions can be empirically verified Treatment effects are local (LATE) Limits external validity Relatively easy to estimate (like RCT) First application: Thistlethwaite and Campbell (1960) 3 / 51 Introduction Thistlethwaite and Campbell Thistlethwaite and Campbell They studied the impact of merit awards on future academic outcomes Awards allocated based on test scores If a person had a score greater than c, the cutoff point, then she received the award Simple way of analyzing: compare those who received the award to those who didn't. (Why is this the wrong approach?) Confounding: factors that influence the test score are also related to future academic outcomes (income, parents' education, motivation) Thistlethwaite and Campbell realized they could compare individuals just above and below the cutoff point. 4 / 51 Introduction Validity Validity Simple idea: assignment mechanism is known We know that the probability of treatment jumps to 1 if test score > c Assumption is that individuals cannot manipulate with precision their assignment variable (think about the SAT) Key word: precision. -

6. Density Estimation 1. Cross Validation 2. Histogram 3. Kernel
6. Density Estimation 6.1 Cross Validation 1. Cross Validation Suppose we observe X1; : : : ; Xn from an unknown density f. Our goal is to estimate f nonparametrically. Finding the best estimator 2. Histogram fn in some sense is equivalent to finding the optimal smoothing 3. Kernel Density Estimation parameter h. b 4. Local Polynomials How to measure the performance of fn? • Risk/Integrated Mean Square Error(IMSE) 5. Higher Dimensions b R(f ; f) = E (L(f ; f)) 6. Mixture Models n n where L(f ; f) = (f (x) − f(x))2dx. 7. Converting Density Estimation Into Regression n n b b • One can find an optimalR estimator that minimizes the risk b b function: fn∗ = argmin R(fn; f); b fn but the risk function isbunknown! b 1 2 Estimation of the Risk function Finding an optimal estimator fn • Use leave-one-out cross validation to estimate the risk function. • E(J(h)) = E(J(h)) = R(h) + cb • One can express the loss function as a function of the smoothing • Theboptimal smoothing parameter parameter h h∗ = argmin J(h) 2 h L(h) = (fn(x) − f(x)) dx Z • Nonparametric estimator f can be expressed as a function of h 2 2 = (fbn(x)) dx − 2 fn(x)f(x)dx + f (x)dx and the best estimator fn∗ can be obtained by Plug-in the Z Z Z b J(h) optimal smoothing parameter b b b • Cross-validation| estimator of the{z risk function }(up to constant) f ∗ = fh∗ 2 2 n b b J(h) = fn(x)dx − f( i)(Xi) n − i=1 Z X b b b t where f( i) is the density estimator obtained after removing i h − observation b 3 4 Theorem 1.