DOCSLIB.ORG

2 Computer Graphics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
2 Computer Graphics 2 Computer Graphics What You Will Learn: The objectives of this chapter are quite ambitious; you should refer to the references cited in each Section to get a deeper explanation of the topics presented. By the end of this chapter you will be familiar with the main building blocks of a 3D graphics interactive application and will be able to use this knowledge to build your own VR projects. In particular, we will give a brief overview of the following topics: • Mathematics: coordinate systems, vectors, and transformation matrices. These are used to represent, visualize, and animate 3D objects, characters, and the like. • 3D modeling: 3D primitives and geometric representations. This is how we actually create objects with a particular 3D shape. • Image rendering: illumination models, lighting, colors and textures. These are used to visualize 3D shapes in a realistic and believable way. This knowledge will give you the foundation required to understand any 3D graphics system, be it a software API like OpenGL or DirectX, a model- ing/animation tool such as Maya, Blender 3D, or 3DS MAX, or a game engine like Torque or Unreal. 2.1 Mathematics 2.1.1 Coordinate Systems A coordinate system is a way to determine the position of a point by a set of numbers (coordinates) that can be distances from a set of reference planes, angles subtended with an origin, or a combination of both [7]. Different coordinate systems have been defined, each of them allows rep- resentation of 3D shapes; however, depending on the shape, it may be easier to represent using one coordinate system than another. The most commonly 12 2 Computer Graphics used coordinate systems are the cartesian and the polar or spherical coordinate systems. Both allow for specifying the position of a point in a 3D Euclidean space, a space in three dimensions just like the world we know. It was named Euclidean after Euclid of Alexandria, a Greek mathematician whose treatise The Elements defined the principles of geometry. There are also non-euclidean geometries, but the kind of shapes we will work with will be represented in a 3D Euclidean space. Cartesian Coordinate Systems This is the most commonly used coordinate system in computers. The position of a point is determined by three distances, from each of the planes. The axes are at right angles (orthogonal) and are typically used to specify spatial dimensions: width, height, and depth (x, y, z). Cartesian coordinates are the most common data to represent real, theoretical, and artistic worlds. Spherical Coordinate Systems A spherical coordinate system is a called polar coordinate system when used in two dimensions. The position of a point is specified using one distance (ρ from the origin) and two angles (θ and φ) measured from the reference planes at right angles (see Figure 2.1a). Spherical coordinates are commonly used in applications that need to define positions relative to the surface of the Earth, such as meteorology, geography, and oceanography. In such cases, the angles are better known as latitude and longitude. The origin is at the center of the planet and the reference planes are the Equator and Greenwich meridian. Spherical coordinates are also used in astronomy to specify the position of celestial objects. In this case, the angles are called right ascension and declination. (a) A point P in spherical (b) A cardioid function in polar co- coordinates (ρ, θ, φ) ordinates Fig. 2.1: Point and shapes in polar coordinates 2.1 Mathematics 13 As shown in Figure 2.1b, some shapes are easier to specify and plot us- ing polar coordinates than using Cartesian coordinates. However, most com- puter visualization systems, which are programmed using graphics APIs like OpenGL, use Cartesian coordinates. Thus, it is necessary to convert positions defined in polar/spherical coordinates to Cartesian coordinates through the following formulas: x = ρ sin φ cos θy= ρ sin φ sin θz= ρ cos φ In the rest of the book we will use Cartesian coordinates; as mentioned earlier, they are the most commonly used and are better “understood” by 3D APIs and other computer graphics-related tools. In general, 3D virtual worlds are created out of 3D polygons, usually trian- gles or squares arranged in 3D space to form 3D surfaces that comprise more complex objects; this is illustrated in Figure 2.2. The simplest polygon and the most efficient to represent, process, and visualize with current graphics hardware is a triangle. A triangle is defined by specifying the three points or vertices that compose it (see Figure 2.2). Commonly available hardware (graphics cards) is able to take these three vertices and use them to draw a colored triangle on the screen at very fast speeds. Currently, graphics cards can draw hundreds of millions of colored triangles per second; for example, the NVIDIA Quadro FX 4600 card can render 250 million triangles per second (March 2007). The complete “drawing” process is called rendering; it involves computing the effects of color and textures assigned to each triangle in addi- tion to lights and possibly shadows and reflections. We explain this process in Section 2.3.4. Fig. 2.2: Triangle-based 3D shape Triangles are the basic primitive for creation of 3D shapes, the building block of virtual worlds. In order to understand how to visualize and animate virtual entities in 3D space we must be able to visualize and animate each triangle comprising the environment in a coherent way. We will provide more details on animation in Chapter 3. 14 2 Computer Graphics 2.1.2 Vectors, Transformations and Matrices To illustrate the basic mathematical principles behind visualization of 3D shapes, we start with a single triangle. In order to represent a triangle shape in a computer we use a Cartesian coordinate system and three points in the space to delimit the shape; we call them vertices. A vertex v is composed of three cartesian coordinates (vx,vy,vz). This set of three coordinates is a 3D vector, an array of three values, which are the vector components. A triangle can thus be defined by three 3D vectors that specify the coordinates of each vertex in the space: v1, v2, v3. In a 3D environment, triangles and any other 3D shape can suffer three basic coordinate transformations: they can be translated, rotated, or scaled. When combined, these three basic transformations allow us to produce a great variety of animation, from simple linear motion to complex trajectories and surface deformations. Some important questions to answer are: how can we translate/rotate/scale a 3D shape? what happens to the vertices forming the shape? Translating a 3D shape means adding a vector T to each of its composing vectors. The addition of two vectors consists of summing each of its compo- nents: a+b = c, where the components of vector c are: (ax+bx,ay+by,az +bz). Scaling affects the components of each vertex by multiplying them by a scale factor s. The components of vector v when scaled by a given factor are (vx × sx,vy × sy,vz × sz). The rotation transformation is a combination of addition and multiplica- tion operations that result from basic trigonometry. It is easier and computa- tionally efficient to use a matrix representation and matrix multiplication to perform a rotation transformation over a vector. In fact, the most convenient way of processing coordinate transformations is to set up matrices containing the parameters of the transformations and use matrix multiplication to reduce a series of transformations to a combined single transformation matrix. Homogeneous Coordinates In order to process transformations in a uniform way, it is necessary to add a component to the vectors and increase the dimensions of the matrices. For 3D space, 4D vectors are used, the four components are called homogeneous coordinates. The components of a 4D homogeneous vector are reduced to three dimensions by the following normalization operation: x, y, z, h −→ x , y , z h h h Any vertex in 3D space can be represented as x, y, z, 1 ;4× 4 matrices should be set up in such a way that multiplying a transformation matrix M by a vector v will give as the result a vector v whose components x,y,z, 1 correspond to the coordinates of v after applying the transformations param- eterized in M. 2.1 Mathematics 15 The fourth dimension (fourth component) will normally remain 1. Most of the graphical transformations can be broken down into products of the three basic ones. Transformation matrices are defined as follows. Translation Vector v , which is the position of v, after a translation of tx units over the X axis, ty units on Y ,andtz units on the Z axis is calculated as follows: ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ 100tx x x + tx ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ 010ty ⎥ ⎢ y ⎥ ⎢ y + ty ⎥ v = T · v = ⎣ ⎦ · ⎣ ⎦ = ⎣ ⎦ 001tz z z + tz 000 1 1 1 When applied to all the vectors (vertices) that comprise a 3D shape, this transformation will move the shape by the magnitude and direction of vector tx,ty,tz . Note that translation cannot be achieved using 3 × 3 matrix mul- tiplication with a 3D vector. This is one of the most important reasons for using homogeneous coordinates: they allow composite transformations to be handled by a single matrix. Scale The scaled version of v is calculated as follows: ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ sx 000 x sx · x ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ 0 sy 00⎥ ⎢ y ⎥ ⎢ sy · y ⎥ v = S · v = ⎣ ⎦ · ⎣ ⎦ = ⎣ ⎦ 00sz 0 z sz · z 0001 1 1 A scaled 3D shape normally changes both its size and its location. Only shapes centered on the origin will remain in the same position. Scaling may also be done with reference to a point Po =[xo,yo,zo], which may be the center of the 3D shape.
Load more

Recommended publications
  • Luna Moth: Supporting Creativity in the Cloud
    Pedro Alfaiate Instituto Superior Técnico / Luna Moth INESC-ID Inês Caetano Instituto Superior Técnico / INESC-ID Supporting Creativity in the Cloud António Leitão Instituto Superior Técnico / INESC-ID 1 ABSTRACT Algorithmic design allows architects to design using a programming-based approach. Current algo- 1 Migration from desktop application rithmic design environments are based on existing computer-aided design applications or building to the cloud. information modeling applications, such as AutoCAD, Rhinoceros 3D, or Revit, which, due to their complexity, fail to give architects the immediate feedback they need to explore algorithmic design. In addition, they do not address the current trend of moving applications to the cloud to improve their availability. To address these problems, we propose a software architecture for an algorithmic design inte- grated development environment (IDE), based on web technologies, that is more interactive than competing algorithmic design IDEs. Besides providing an intuitive editing interface which facilitates programming tasks for architects, its performance can be an order of magnitude faster than current aalgorithmic design IDEs, thus supporting real-time feedback with more complex algorithmic design programs. Moreover, our solution also allows architects to export the generated model to their preferred computer-aided design applications. This results in an algorithmic design environment that is accessible from any computer, while offering an interactive editing environment that inte- grates into the architect’s workflow. 72 INTRODUCTION programming languages that also support traceability between Throughout the years, computers have been gaining more ground the program and the model: when the user selects a component in the field of architecture. In the beginning, they were only used in the program, the corresponding 3D model components are for creating technical drawings using computer-aided design highlighted.
    [Show full text]
  • 3D Modeling: Surfaces
    CS 430/536 Computer Graphics I Overview • 3D model representations 3D Modeling: • Mesh formats Surfaces • Bicubic surfaces • Bezier surfaces Week 8, Lecture 16 • Normals to surfaces David Breen, William Regli and Maxim Peysakhov • Direct surface rendering Geometric and Intelligent Computing Laboratory Department of Computer Science Drexel University 1 2 http://gicl.cs.drexel.edu 1994 Foley/VanDam/Finer/Huges/Phillips ICG 3D Modeling Representing 3D Objects • 3D Representations • Exact • Approximate – Wireframe models – Surface Models – Wireframe – Facet / Mesh – Solid Models – Parametric • Just surfaces – Meshes and Polygon soups – Voxel/Volume models Surface – Voxel – Decomposition-based – Solid Model • Volume info • Octrees, voxels • CSG • Modeling in 3D – Constructive Solid Geometry (CSG), • BRep Breps and feature-based • Implicit Solid Modeling 3 4 Negatives when Representing 3D Objects Representing 3D Objects • Exact • Approximate • Exact • Approximate – Complex data structures – Lossy – Precise model of – A discretization of – Expensive algorithms – Data structure sizes can object topology the 3D object – Wide variety of formats, get HUGE, if you want each with subtle nuances good fidelity – Mathematically – Use simple – Hard to acquire data – Easy to break (i.e. cracks represent all primitives to – Translation required for can appear) rendering – Not good for certain geometry model topology applications • Lots of interpolation and and geometry guess work 5 6 1 Positives when Exact Representations Representing 3D Objects • Exact
    [Show full text]
  • Full Body 3D Scanning
    3D Photography: Final Project Report Full Body 3D Scanning Sam Calabrese Abhishek Gandhi Changyin Zhou fsmc2171, asg2160, [email protected] Figure 1: Our model is a dancer. We capture his full-body 3D model by combining image-based methods and range scanner, and then do an animation of dancing. Abstract Compared with most laser scanners, image-based methods using triangulation principles are much faster and able to provide real- In this project, we are going to build a high-resolution full-body time 3D sensing. These methods include depth from motion [Aloi- 3D model of a live person by combining image-based methods and monos and Spetsakis 1989], shape from shading [Zhang et al. laser scanner methods. A Leica 3D range scanner is used to obtain 1999], depth from defocus/focus [Nayar et al. 1996][Watanabe and four accurate range data of the body from four different perspec- Nayar 1998][Schechner and Kiryati 2000][Zhou and Lin 2007], and tives. We hire a professional model and adopt many measures to structure from stereo [Dhond and Aggarwal 1989]. They often re- minimize the movement during the long laser-scanning. The scan quire the object surface to be textured, non-textured, or lambertian. data is then sequently processed by Cyclone, MeshLab, Scanalyze, These requirements often make them impractical in many cases. VRIP, PlyCrunch and 3Ds Max to obtain our final mesh. We take In addition, image-based methods usually cannot give a precision three images of the face from frontal and left/right side views, and depth estimation since they do patch-based analysis.
    [Show full text]
  • Bonus Ch. 2 More Modeling Techniques
    Bonus Ch. 2 More Modeling Techniques When it comes to modeling in modo, the sky is the limit. This book is designed to show you all of the techniques available to you, through written word and visual examples on the DVD. This chapter will take you into another project, in which you’ll model a landscape. From there, you’ll texture it, and later you’ll add the environment. You’ll see how modo’s micro polygon displacement works and how powerful it is. From there, you’ll create a cool toy gun. The techniques used in this project will show you how to create small details that make the model come to life. Then, you’ll learn to texture the toy gun to look like real plastic. Building a Landscape Landscapes traditionally have been a chore for 3D artists. This is because to prop- erly create them, you need a lot of geometry. A lot of geometry means a lot of polygons, and a lot of polygons means a lot of render time. But the team at Luxology has introduced micro polygon displacement in modo 201/202, allow- ing you to create and work with simple objects, but render with millions of poly- gons. How is this possible? The micro polygon displacement feature generates additional polygons at render time. The goal is that finer details can be achieved without physically modeling them into the base object. You can then add to the details achieved through micro poly displacements with modo’s bump map capabilities and generate some terrific-looking models.
    [Show full text]
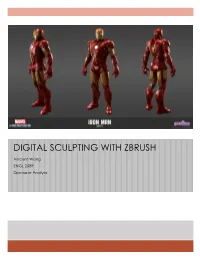
  • Digital Sculpting with Zbrush
    DIGITAL SCULPTING WITH ZBRUSH Vincent Wang ENGL 2089 Discourse Analysis 2 ZBrush Analysis Table of Contents Context ........................................................................................................................... 3 Process ........................................................................................................................... 5 Analysis ........................................................................................................................ 13 Application .................................................................................................................. 27 Activity .......................................................................................................................... 32 Works Cited .................................................................................................................. 35 3 Context ZBrush was created by the Pixologic Inc., which was founded by Ofer Alon and Jack Rimokh (Graphics). It was first presented in 1999 at SIGGRAPH (Graphics). Version 1.5 was unveiled at the MacWorld Expo 2002 in New York and SIGGRAPH 2002 in San Antonio (Graphics). Pixologic, the company describes the 3D modeling software as a “digital sculpting and painting program that has revolutionized the 3D industry…” (Pixologic). It utilizes familiar real-world tools in a digital environment, getting rid of steep learning curves and allowing the user to be freely creative instead of figuring out all the technical details. 3D models that are created in
    [Show full text]
  • 3D Modeling and the Role of 3D Modeling in Our Life
    ISSN 2413-1032 COMPUTER SCIENCE 3D MODELING AND THE ROLE OF 3D MODELING IN OUR LIFE 1Beknazarova Saida Safibullaevna 2Maxammadjonov Maxammadjon Alisher o’g’li 2Ibodullayev Sardor Nasriddin o’g’li 1Uzbekistan, Tashkent, Tashkent University of Informational Technologies, Senior Teacher 2Uzbekistan, Tashkent, Tashkent University of Informational Technologies, student Abstract. In 3D computer graphics, 3D modeling is the process of developing a mathematical representation of any three-dimensional surface of an object (either inanimate or living) via specialized software. The product is called a 3D model. It can be displayed as a two-dimensional image through a process called 3D rendering or used in a computer simulation of physical phenomena. The model can also be physically created using 3D printing devices. Models may be created automatically or manually. The manual modeling process of preparing geometric data for 3D computer graphics is similar to plastic arts such as sculpting. 3D modeling software is a class of 3D computer graphics software used to produce 3D models. Individual programs of this class are called modeling applications or modelers. Key words: 3D, modeling, programming, unity, 3D programs. Nowadays 3D modeling impacts in every sphere of: computer programming, architecture and so on. Firstly, we will present basic information about 3D modeling. 3D models represent a physical body using a collection of points in 3D space, connected by various geometric entities such as triangles, lines, curved surfaces, etc. Being a collection of data (points and other information), 3D models can be created by hand, algorithmically (procedural modeling), or scanned. 3D models are widely used anywhere in 3D graphics.
    [Show full text]
  • Using Depth Cameras for Dense 3D Modeling of Indoor Environments
    RGB-D Mapping: Using Depth Cameras for Dense 3D Modeling of Indoor Environments Peter Henry1, Michael Krainin1, Evan Herbst1, Xiaofeng Ren2, Dieter Fox1;2 Abstract RGB-D cameras are novel sensing systems that capture RGB images along with per-pixel depth information. In this paper we investigate how such cam- eras can be used in the context of robotics, specifically for building dense 3D maps of indoor environments. Such maps have applications in robot navigation, manip- ulation, semantic mapping, and telepresence. We present RGB-D Mapping, a full 3D mapping system that utilizes a novel joint optimization algorithm combining visual features and shape-based alignment. Visual and depth information are also combined for view-based loop closure detection, followed by pose optimization to achieve globally consistent maps. We evaluate RGB-D Mapping on two large indoor environments, and show that it effectively combines the visual and shape informa- tion available from RGB-D cameras. 1 Introduction Building rich 3D maps of environments is an important task for mobile robotics, with applications in navigation, manipulation, semantic mapping, and telepresence. Most 3D mapping systems contain three main components: first, the spatial align- ment of consecutive data frames; second, the detection of loop closures; third, the globally consistent alignment of the complete data sequence. While 3D point clouds are extremely well suited for frame-to-frame alignment and for dense 3D reconstruc- tion, they ignore valuable information contained in images. Color cameras, on the other hand, capture rich visual information and are becoming more and more the sensor of choice for loop closure detection [21, 16, 30].
    [Show full text]
  • 3D Computer Graphics Compiled By: H
    animation Charge-coupled device Charts on SO(3) chemistry chirality chromatic aberration chrominance Cinema 4D cinematography CinePaint Circle circumference ClanLib Class of the Titans clean room design Clifford algebra Clip Mapping Clipping (computer graphics) Clipping_(computer_graphics) Cocoa (API) CODE V collinear collision detection color color buffer comic book Comm. ACM Command & Conquer: Tiberian series Commutative operation Compact disc Comparison of Direct3D and OpenGL compiler Compiz complement (set theory) complex analysis complex number complex polygon Component Object Model composite pattern compositing Compression artifacts computationReverse computational Catmull-Clark fluid dynamics computational geometry subdivision Computational_geometry computed surface axial tomography Cel-shaded Computed tomography computer animation Computer Aided Design computerCg andprogramming video games Computer animation computer cluster computer display computer file computer game computer games computer generated image computer graphics Computer hardware Computer History Museum Computer keyboard Computer mouse computer program Computer programming computer science computer software computer storage Computer-aided design Computer-aided design#Capabilities computer-aided manufacturing computer-generated imagery concave cone (solid)language Cone tracing Conjugacy_class#Conjugacy_as_group_action Clipmap COLLADA consortium constraints Comparison Constructive solid geometry of continuous Direct3D function contrast ratioand conversion OpenGL between
    [Show full text]
  • Extents and Limitations of 3D Computer Models for Graphic Analysis of Form and Space in Architecture SALEH UDDIN, Mohammed University of Missouri-Columbia, U.S.A
    Go to contents 18 Extents and Limitations of 3D Computer Models for Graphic Analysis of Form and Space in Architecture SALEH UDDIN, Mohammed University of Missouri-Columbia, U.S.A. http://web.missouri.edu/~envugwww/faculty.html http://web.missouri.edu/~uddinm This paper investigates the strength and limitations of basic 3D diagrammatic models and their related motion capabilities in the context of graphic analysis. The focus of such analysis is to create a computer based environment to represent visual analysis of architectural form and space. The paper highlights the restrictions that were found in a specific 3D-computer model environment to satisfy a basic diagrammatic need for analysis. Motion related features that take into account of parametric changes are also investigated to help enhance representation of analytic models. Acknowledging the restrictions, it can be stated that computational media are the only ones at present that can create an interactive multimedia format using components constructed through various computational techniques Keywords: 3D Model, Analytic Diagram, Motion Model, Form Analysis, Design Principles. Analysis points’ and also supported the theoretical model. Throughout history, the notion of ‘precedent’ has Thus, it can be said that an analysis is an abstract always provided conceptual models to serve the quest process of simplification that reduces a total work into for appropriate architectural forms. It is a relatively its essential elements. In architecture, the primary goal recent phenomenon that considers architecture of a design analysis and its representation is to expose through a veil of literary metaphors. Since the end the underlying concept, organizational pattern, design product of architecture is a built outcome, the most characteristics, and ‘tectonics’ through simplified basic theoretical stance must be supported in turn by diagrams.
    [Show full text]
  • Multi-Resolution Surfel Maps for Efficient Dense 3D Modeling And
    Journal of Visual Communication and Image Representation 25(1):137-147, Springer, January 2014, corrected Table 3 & Sec 6.2. Multi-Resolution Surfel Maps for Efficient Dense 3D Modeling and Tracking J¨orgSt¨uckler and Sven Behnke Autonomous Intelligent Systems, Computer Science Institute VI, University of Bonn, Friedrich-Ebert-Allee 144, 53113 Bonn, Germany fstueckler, [email protected] Abstract Building consistent models of objects and scenes from moving sensors is an important prerequisite for many recognition, manipulation, and navigation tasks. Our approach integrates color and depth measurements seamlessly in a multi-resolution map representation. We process image sequences from RGB-D cameras and consider their typical noise properties. In order to align the images, we register view-based maps efficiently on a CPU using multi- resolution strategies. For simultaneous localization and mapping (SLAM), we determine the motion of the camera by registering maps of key views and optimize the trajectory in a probabilistic framework. We create object models and map indoor scenes using our SLAM approach which includes randomized loop closing to avoid drift. Camera motion relative to the acquired models is then tracked in real-time based on our registration method. We benchmark our method on publicly available RGB-D datasets, demonstrate accuracy, efficiency, and robustness of our method, and compare it with state-of-the- art approaches. We also report on several successful public demonstrations where it was used in mobile manipulation tasks. Keywords: RGB-D image registration, simultaneous localization and mapping, object modeling, pose tracking 1. Introduction Robots performing tasks in unstructured environments must estimate their pose in reference to objects and parts of the environment.
    [Show full text]
  • Autodesk 3Ds Max Design Fundamentals
    Autodesk® 3ds Max® Design Fundamentals Course Length: 4 days The Autodesk® 3ds Max® Fundamentals training course provides a thorough introduction to the Autodesk 3ds Max software that will help new users make the most of this sophisticated application, as well as broaden the horizons of existing, self-taught users. The practices in this training course are geared towards real-world tasks encountered by the primary users of the Autodesk 3ds Max software: professionals in the Architecture, Interior Design, Civil Engineering, and Product Design industries. The main topics include: Introduction to Autodesk 3ds Max Autodesk 3ds Max Interface and Workflow Assembling Files by importing, linking, or merging 3D Modeling with Primitives and 2D Objects Using Modifiers to create and modify 3D objects Materials and Maps Autodesk 3ds Max Lighting Lighting and Rendering with mental ray Rendering and Cameras Animation for Visualization Course description shown for Autodesk 3ds Max 2016.Topics, curriculum, and/or prerequisites may change depending on software version. Prerequisites: Experience with 3D modeling is recommended. Training Guide Contents Chapter 1: Introduction to Autodesk 3ds Max Overview Visualization Workflow The Autodesk 3ds Max Interface Preferences Setting the Project Folder Configure Paths Display Drivers Viewport Display and Labels Chapter 2: Autodesk 3ds Max Configuration Viewport Navigation Viewport Configuration Object Selection Methods Units Setup Layer and Object Properties Chapter 3: Assembling Project Files Data Linking and Importing Linking Files References Chapter 4: Basic Modeling Techniques Model with Primitives Modifiers and Transforms Sub-Object Mode Reference Coordinate Systems and Transform Centers Cloning and Grouping Polygon Modeling Tools in the Ribbon Statistics in Viewport Course description shown for Autodesk 3ds Max 2016.
    [Show full text]
  • Architectural Visualization Produce Accurate, Beautiful, High-Quality Architectural Renderings
    Architectural Visualization Produce accurate, beautiful, high-quality architectural renderings Image courtesy of Valentin Studio “Having such powerful tools places more focus on us to do the best job possible through creating alluring moods and lighting spaces more effectively.” Ben Rappell, FKD Studio Autodesk 3ds Max enables architects, designers, and visualization specialists to fully explore, validate and communicate their creative ideas, from concept models to cinema-quality visualizations. A comprehensive 3D modeling, animation and rendering solution, 3ds Max delivers powerful lighting simulation and analysis technology, advanced rendering capabilities, and a faster, more integrated workflow. 3ds Max provides a powerful way to sharpen your competitive edge, visually communicate your client’s proposed designs, and beautifully tell their story with realistic elements and details. Bring architectural visualizations to life – with everything from interior walkthroughs to exterior environments, fully populated with roads, buildings, and landscapes, and animated with cars, people, and natural elements. Image courtesy of Joe Ong Why you’ll love 3ds Max TRANSFORM TECHNICAL TO VISUAL 3ds Max offers a rich and flexible toolset to model premium architectural designs, allowing full artistic control to translate technical drawings into visual stories. Image courtesy of Valentin Studio Key benefits Inspire, communicate, and sell your vision with detailed environments, objects, and embellishments. HIGH QUALITY IMAGERY Advanced tools in 3ds Max give you the built-in rendering power to create the highest quality photo-real visualizations and create a premium experience for clients to envision their future investment. EMBELLISH EVERY DETAIL 3ds Max allows you to bring to life fine-tuned extra touches such as cars, people, and vegetation, for an enriched and engaging experience that enhances the architecture and its surrounding landscape.
    [Show full text]