A Method for the Improvement Elevation Data Generated from Automated Photogrammetric Methods Into Sis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

(MSGIST) 2014 Resume Book
Master of Science of Geographic Information Systems Technology (MSGIST) 2014 Resume Book University of Arizona Geographic Information Systems Technology (GIST) School of Geography and Development University of Arizona • P.O. Box 210076 • Tucson, AZ 85721 • uagist.arizona.edu Select 2014 MSGIST Students Jessica Styron Abrahams Leanndra Arechederra‐Romero William Beaver Shane Clark Cassie Fausel Gwynn Harlowe Pankaj Jamwal Jessica Fraver Michael Levengood Manny Lizarraga Brett Stauffer Jamie Velkoverh Nathan Wasserman RESUMES Jessica Styron Abrahams (formerly Jessica Alicia Styron) 2002 East River Road, Apt. S10 Tucson, AZ 85718 Mobile: (925) 451‐6289 Qualifications 01/2014 – 12/2014 University of Arizona, Tucson, Arizona. Qualification Masters of Science in GIS Technology (expected 12/2014) 08/2009 – 12/2001 University of Arizona, Tucson, Arizona. Qualification Masters of Science in Planning 04/2002 – 07/2003 Chapman University (Concord Campus), Orange, California. Qualification: Single Subject Credential in French with Supplementary Authorization in Introductory English 08/1997 – 12/2001 University of California at Berkeley, Berkeley, California. Qualification: Bachelors of Arts in French and in Comparative Literature. Between August 1999 – June 2000, Participated in the Education Abroad Program in Grenoble, France and attended the Université de Grenoble III, Stendhal. I graduated with a GPA of 3.44. Employment 03/2014 – 12/2014 BAIR Analytics, Inc. Highlands Ranch, Colorado. Intern. Main duties: Extracted and transformed vector shapefiles in GIS to create topographical maps. 03/2011 – 08/2011 City and County of San Francisco, Recreation and Parks Department, Planning Division, San Francisco, California. Student Design Trainee 1 Main duties: Reviewed and responded to CEQA and NEPA documents for projects impacting Recreation & Parks Department (RPD) facilities; Researched and summarized best management practices; Tracked and summarized U.S. -
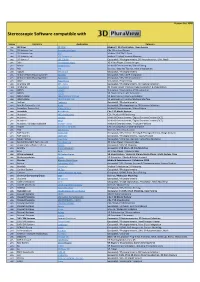
Stereo Software List
Version: Oct. 2020 Stereoscopic Software compatible with Stereo Company Application Category yes 3D Slicer 3D Slicer Medical / 3D Visualization, Open Source Yes 3D Systems, Inc. Geomagic Freeform CAx / Freeform Design yes 3D Systems, Inc. D2P Medical / DICOM-2-Print yes 3D Systems, Inc. VSP Technology Medical / Virtual Surgical Planning yes 3DFlow s.r.l. 3DF ZEPHYR Geospatial / Photogrammetry, 3D Reconstruction, UAV, Mesh yes 3dtv Stereoscopic Player 3D Video Player / Stereo Images yes Adobe Premiere Pro Media & Entertainment / Video Editing yes AGI STK Science / Satellite Tool Kit, Orbit Visualization yes Agisoft Metashape Geospatial / Photogrammetry yes AirborneHydroMapping GmbH KomVISH Geospatial / GIS, LiDAR Integration yes AirborneHydroMapping GmbH HydroVISH Geospatial / GIS, SDK Visualization yes Altair HyperWorks Simulation / Engineering yes Analytica Ltd DPS - Delta Geospatial / Photogrammetry, 3D Feature Collection FULL Anchorlab StereoBlend 3D Image Viewer / Stereo Image Generation & Visualization yes ANSYS EnSight Simulation / Engineering, VR Visualization yes ANSYS SPEOS VR Engineering / Light Simulation yes ANSYS Optis VREXPERIENCE SCANeR VR Engineering / Driving Simulation yes ANSYS Optis VRXPERIENCE HMI VR Engineering / Human Machine Interface yes Aplitop TcpStereo Geospatial / Photogrammetry yes Asia Air Survey Co., Ltd. Azuka Geospatial / Photogrammetry, 3D Feature Collection yes Assimilate Europe Ltd. SCRATCH Vs. 9 Media & Entertainment / Video Editing yes Autodesk NavisWorks CAx / 3D Model Review yes Autodesk VRED Professional -

Stereo Processing of Planetary Stereo Imagery Using ISIS3 and SOCET SET®
Stereo Processing of Planetary Stereo Imagery using ISIS3 and SOCET SET® a Primer Astrogeology Science Center, USGS Table of Content Stereo Processing ......................................................................................................................................... 1 of Planetary Stereo Imagery ......................................................................................................................... 1 using ISIS3 and SOCET SET® ..................................................................................................................... 1 a Primer ......................................................................................................................................................... 1 Table of Content ..................................................................................................................................... 2 1. Photogrammetry ........................................................................................................... 5 1.1 The Colinearity Condition ....................................................................................................... 5 1.2 Sensor Models ......................................................................................................................... 6 1.3 Surface Extraction, DEM, DTM, DSM, and TIN ...................................................................... 7 1.4 Orthorectification ................................................................................................................. -

Producing LROC NAC Dtms in SOCET SET (And SOCET GXP)
Producing LROC NAC DTMs in SOCET SET (and SOCET GXP) Madeleine Manheim1, Trent Hare2 -- [email protected] 1Arizona State University, 2USGS March 3, 2021 LSIC Workshop on Lunar Mapping for Precision Landing Introduction ● LRO launched June 2009 ○ 50 km circular polar orbit Sept. 2009 – Dec. 2011 ○ Currently in elliptical polar orbit (80 x 108 km) ● 2 Narrow Angle Cameras (NACs) ○ 2 panchromatic linear pushbroom cameras ○ 2.86° FOV / camera ○ 0.5 - 2.0 meters/pixel ● Lunar Orbiter Laser Altimeter (LOLA) ○ Most accurate global positioning data ○ Uncertainty <10 m horizontally, and <1 m vertically ● Digital Terrain Models are produced using: ○ Integrated Software for Imagers and Spectrometers (ISIS) ○ SOCET SET by BAE Systems Stereo pairs acquired from consecutive orbits Data Sources Narrow Angle Cameras (NACs) Lunar Orbiter Laser Altimeter • 2 panchromatic linear pushbroom (LOLA) cameras • time-of-flight altimeter • use targeted stereo observations, • single pulse illuminates a 5-spot pattern on taken on sequential orbits the surface • Provides dense and precise source of ~10 cm nominal precision of 28 Hz pulse topographic data • • precision orbit determination using LOLA profiles and the GRAIL gravity model provides global data with positional uncertainty <10 m horizontally, and <1 m vertically • provides most accurate global positioning data LROC NAC Camera Stereo Pair Acquisition Illumination conditions: ● Incidence angle: ~50° (40°-65°), avoiding deep shadows when possible ● Emission angle: <~45° (can be greater for smoother slopes) -

SOCET GXP | Brochure
Geospatial eXploitation Products™ SOCET GXP ® Integrated with the GXP Xplorer® Platform Geospatial eXploitation Products™ SOCET GXP ® Seamlessly integrated with the GXP Xplorer Platform, SOCET GXP allows users to stream imagery in multiple formats directly into a Multiport for exploitation. Once analysis is completed, users Create geospatial products from imagery, terrain, LiDAR, video and more can easily publish final products back to their GXP Xplorer® catalog, allowing for subsequent Utilize airborne or satellite imagery to create 3-D models and plan future construction discovery by the entire federated user base. Monitor infrastructure corridors and communication networks to detect potential issues The Workflow Improvement Module (WIM) integrates the GXP Xplorer catalog directly with the Coordinate operational missions and designate troop maneuvers SOCET GXP Multiport for efficient geospatial queries enabling users to discover content while Rapidly produce intelligence reports in a variety of formats enabling critical decisions eliminating the need to switch between applications. Reduce costly data search efforts SOCET GXP is an advanced geospatial intelligence software solution that Statistics show that analysts spend up to 50 percent of utilizes imagery from satellite and aerial sources to identify, analyze, and extract their time locating imagery and data across disparate ground features, allowing for rapid product creation. Image analysis, advanced systems, networks, and geographic locations. photogrammetric techniques, remote sensing, and feature collection workflows By combining SOCET GXP with GXP Xplorer and are seamlessly combined into one comprehensive package. the WIM, your production time will decrease, your productivity will increase, and your organization will Supporting multiple projects and missions, SOCET GXP workflows are designed save both time and money. -

Accuracy Assessment of Photogrammetric Digital Elevation
ACCURACY ASSESSMENT OF PHOTOGRAMMETRIC DIGITAL ELEVATION MODELS GENERATED FOR THE SCHULTZ FIRE BURN AREA By Danna K. Muise A Thesis Submitted in Partial Fulfillment of the Requirements for the degree of Master of Science in Applied Geospatial Sciences Northern Arizona University August 2014 Approved: Erik Schiefer, Ph.D., Chair Ruihong Huang, Ph.D. Mark Manone, M.A. Abstract ACCURACY ASSESSMENT OF PHOTOGRAMMETRIC DIGITAL ELEVATION MODELS GENERATED FOR THE SCHULTZ FIRE BURN AREA Danna K. Muise This paper evaluates the accuracy of two digital photogrammetric software programs (ERDAS Imagine LPS and PCI Geomatica OrthoEngine) with respect to high- resolution terrain modeling in a complex topographic setting affected by fire and flooding. The site investigated is the 2010 Schultz Fire burn area, situated on the eastern edge of the San Francisco Peaks approximately 10 km northeast of Flagstaff, Arizona. Here, the fire coupled with monsoon rains typical of northern Arizona drastically altered the terrain of the steep mountainous slopes and residential areas below the burn area. To quantify these changes, high resolution (1 m and 3 m) digital elevation models (DEMs) were generated of the burn area using color stereoscopic aerial photographs taken at a scale of approximately 1:12000. Using a combination of pre-marked and post-marked ground control points (GCPs), I first used ERDAS Imagine LPS to generate a 3 m DEM covering 8365 ha of the affected area. This data was then compared to a reference DEM (USGS 10 m) to evaluate the accuracy of the resultant DEM. Findings were then divided into blunders (errors) and bias (slight differences) and further analyzed to determine if different factors (elevation, slope, aspect and burn severity) affected the accuracy of the DEM. -

Performance Assessment of Automated Feature Extraction Tools on High Resolution Imagery
PERFORMANCE ASSESSMENT OF AUTOMATED FEATURE EXTRACTION TOOLS ON HIGH RESOLUTION IMAGERY Daniel A. Lavigne, Defence Scientist Defence Research and Development Canada – Valcartier 2459, Pie-XI Blvd. North Quebec (Quebec), CANADA G3J 1X5 [email protected] Gang Hong Yun Zhang Department of Geodesy and Geomatics Engineering University of New Brunswick 15 Dineen Dr., P.O. Box 4400 Fredericton (New-Brunswick), CANADA E3B 5A3 [email protected] [email protected] ABSTRACT The enormous increase in the volume of remotely sensed data that is being acquired by an ever-growing number of earth observation sensors, led to the situation where the image analysts are at risk to be overwhelmed by the number of images to process. A way to cope with this situation is to use automated feature extraction (AFE) tools to help the image analysts in the extraction of geospatial features, and address specific tasks such as object detection for change detection purposes. However, it is not clear which AFE tools perform better against others, and on what scenarios. This paper presents an assessment of the performance of three AFE tools to extract man-made objects for change detection on high resolution airborne and spaceborne electro-optic imagery: Feature Analyst (Visual Learning Systems Inc.), eCognition (Definiens AG), and Genie Pro (U.S. Los Alamos National Laboratory). These tools all intend to assist the image analysts in extracting relevant image features using dissimilar feature extraction algorithms. Feature Analyst employs machine learning techniques to extract user-defined features; eCognition is an object-oriented classification package using a fuzzy logic scheme; Genie Pro is an evolutionary computation software system assembling image processing tools from a collection of image operators by means of genetic algorithms. -

The Use of High Resolution Satellite Data (Eg IKONOS)
The use of high resolution satellite data (IKONOS) in the establishment and maintenance of an urban Geographical Information System. Masters of Engineering (Surveying and Spatial Information Systems) Eric W Richards January 2009 Originality Statement ‘I hereby declare that this submission is my own work and to the best of my knowledge it contains no materials previously published or written by another person, or substantial proportions of material which have been accepted for the award of any other degree or diploma at UNSW or any other educational institution, except where due acknowledgement is made in the thesis. Any contribution made to the research by others, with whom I have worked at UNSW or elsewhere, is explicitly acknowledged in the thesis. I also declare that the intellectual content of this thesis is the product of my own work, except to the extent that assistance from others in the project’s design and conception or in style, presentation and linguistic expression is acknowledged.’ Signed………………………………………………….. Date…………………………………………………….. i Acknowledgements For an activity lasting this long it is needless to say there are a number of people who have played a part in its final completion, some of whom may or may not know they played a part. I must first thank the staff at the University of NSW such as Brian Donnelly and Helve who accommodated my arrivals, stays and departures to and from Canberra. A major vote of appreciation goes to my supervisor Dr John Trinder who has shown significant patience and has always provided timely and well needed feedback and advice by correspondence, particularly after the unfortunate passing of Dr Ewan Masters early in my starting of this study.