DOCSLIB.ORG

Computing with Simple Lie Algebras Version 1.5.3

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Computing with Simple Lie Algebras Version 1.5.3 SLA Computing with simple Lie algebras Version 1.5.3 15 November 2019 Willem Adriaan de Graaf Willem Adriaan de Graaf Email: [email protected] Homepage: http://www.science.unitn.it/~degraaf SLA 2 Abstract This package provides functions for computing with various aspects of the theory of simple Lie algebras in characteristic zero. Copyright © 2013-2018 Willem de Graaf Contents 1 Introduction 4 2 Auxiliary Functions5 2.1 Root Systems......................................5 2.2 Weyl groups......................................6 2.3 Lie Algebras and Their Modules............................8 3 Nilpotent Orbits 11 3.1 The functions...................................... 12 4 Finite Order Automorphisms and q-Groups 16 4.1 The functions...................................... 16 5 Semisimple Subalgebras of Semisimple Lie Algebras 22 5.1 Branching........................................ 22 5.2 Constructing Semisimple Subalgebras......................... 23 References 30 Index 31 3 Chapter 1 Introduction This package is a collection of functions that I wrote for various research projects (e.g., [Gra08], [dG11], [GE09], [Gra11], [dGVY12]). The reason to collect them in a package is to avoid them getting lost. Secondly, I believe that the functions may be of wider interest. Apart from this one, this manual has four chapters. The second describes various functions that did not fit in any of the other chapters. They vary from short utility functions to functions implementing rather complex algorithms. The remaining three chapters are all devoted to a particular area. The third chapter contains (descriptions of) functions for computing with the classification of the nilpotent orbits in simple Lie algebras. There are functions for creating the orbits and for computing representatives. We refer to [CM93] for an overview of the theory of nilpotent orbits in simple Lie algebras. The fourth chapter is dedicated to finite order automorphisms of the simple Lie algebras and the corresponding q-groups. The finite order automorphisms have been classified by Kac, up to conju- gacy in the automorphism group. For the background on this we refer to [Hel78]. The classification is described in terms of so-called Kac diagrams. The package contains a function for creating all automorphisms of a given simple Lie algebra, of a given finite order. The eigenspaces of an automorphism of finite order of a simple Lie algebra form a grading of that Lie algebra. Moreover, the 0-component is a reductive subalgebra, acting on the 1-component. The 0-component corresponds to a reductive reductive group, also acting on the 1-component. This group (with its action) is called a q-group. It was introduced and studied in the 70-s by Vinberg ([Vin75], [Vin76], [Vin79]) The package has a function for listing the nilpotent orbits of this group. The fifth chapter has functions for working with semisimple subalgebras of semisimple Lie alge- bras. The package contains a database of semisimple subalgebras of the simple subalgebras of ranks up to 8. Moreover, there are functions for computing the semisimple subalgebras of semisimple Lie algebras on the fly. Finally, there are some functions for computing branching rules. We remark that the package needs the package QuaGroup. 4 Chapter 2 Auxiliary Functions This chapter contains the description of some functions that do not fit in any other chapter. 2.1 Root Systems 2.1.1 ExtendedCartanMatrix . ExtendedCartanMatrix(R) (operation) Here R is a root system. This function returns the extended Cartan matrix of R. That is the Cartan matrix correponding to the lowest root (coming first), and the simple roots of R. The output is a record with components ECM (the extended Cartan matrix) and labels (the labels of the corresponding Dynkin diagram; they are the integer coefficients of a linear dependency of the roots corresponding to the nodes). Example gap> R:= RootSystem("F",4);; gap> ExtendedCartanMatrix(R); rec( ECM := [ [ 2, -1, 0, 0, 0 ], [ -1, 2, -1, 0, 0 ], [ 0, -1, 2, -2, 0 ], [ 0, 0, -1, 2, -1 ], [ 0, 0, 0, -1, 2 ] ], labels := [ 1, 2, 3, 4, 2 ] ) 2.1.2 CartanType . CartanType(C) (operation) Here C is a Cartan matrix (i.e., an integer matrix with 2-s on the diagonal, non-positive entries otherwise, and there exists a diagonal integer matrix D such that CD is a positive definite symmetric matrix). This function returns a record with two components: types, a list containing the types of the simple components of the corresponding root system, and enumeration, a standard enumeration of the vertices of the Dynkin diagram of C. So this can be used to construct isomorphisms of root systems. Example gap> C:= [[2,0,-3,0],[0,2,0,-1],[-1,0,2,0],[0,-1,0,2]]; [ [ 2, 0, -3, 0 ], [ 0, 2, 0, -1 ], [ -1, 0, 2, 0 ], [ 0, -1, 0, 2 ] ] gap> CartanType(C); rec( enumeration := [ [ 3, 1 ], [ 2, 4 ] ], types := [ [ "G", 2 ], [ "A", 2 ] ] ) 5 SLA 6 2.2 Weyl groups 2.2.1 WeylTransversal . WeylTransversal(R, inds) (operation) . WeylTransversal(R, roots) (operation) Here R is a root system, and inds a list of indices of positive roots of R that form a set of simple roots of a root subsystem of R (the system does not check this). Here an index of a positive root is its position in the list PositiveRootsNF( R ). This function returns a list of shortest representatives of the right cosets of the corresponding Weyl subgroup of the Weyl group of R. The elements of the Weyl group are given as reduced expressions. In the second form rts is a list of roots of R, that form a set of simple roots of a root subsystem of R (again, this is not checked). In this form the roots so not have to be positive. They have to be represented with respect to the basis of simple roots, i.e., they are elements of PositiveRootsNF(R) or of NegativeRootsNF(R). Example gap> R:= RootSystem("A",3);; gap> WeylTransversal( R, [2,6] ); [ [ ], [ 1 ], [ 3 ], [ 1, 2 ], [ 1, 3 ], [ 3, 2 ] ] gap> R:= RootSystem("E",8);; gap> p:= PositiveRootsNF(R);; gap> a:= WeylTransversal( R, [p[1],p[3],p[4],p[5],p[6],p[7],p[8],-p[120]] );; gap> Length(a); 1920 2.2.2 SizeOfWeylGroup . SizeOfWeylGroup(R) (operation) . SizeOfWeylGroup(type) (operation) . SizeOfWeylGroup(X, n) (operation) In the first from R is a root system. In the second form type is a list of lists describing the type of a root system. For example: [["A",3],["B",5],["G",2]]. In the third form X is a letter (i.e., a string) and n a positive integer, so that Xn is the type of a root system. In all cases the number of elements of the Weyl group is returned. Example gap> R:= RootSystem( SimpleLieAlgebra("E",6,Rationals) );; gap> SizeOfWeylGroup(R); 51840 gap> SizeOfWeylGroup( [["E",6]] ); 51840 gap> SizeOfWeylGroup( "E", 6 ); 51840 2.2.3 WeylGroupAsPermGroup . WeylGroupAsPermGroup(R) (operation) SLA 7 Here R is a root system. This function returns a permutation group whose set of elements is in bijection with the set of elements of the Weyl group of R. More precisely, this bijection works as follows. Let n be the number of positive roots of R. We list the positive roots in the order in which they apppear in PositiveRootsNF( R ). To this list we append the negative roots, listed in the same order. Thus the list of roots is fa1;:::;a2ng, where ai+n = −ai for 1 ≤ i ≤ n. Then a reflection sa corresponding to the root a corresponds to the permutation pa , where sa (ai) = aipa . Note, however, that sa acts from the left, whereas pa acts from the right. Let W denote the Weyl group of R and let G be the group generated by the permutations pa for a in the fixed set of simple roots of R. Then mapping sa to pa extends to an anti-isomorphism W ! G. The reason for doing it like this is that in the vast majority of literature on Lie theory the Weyl group acts from the left, but in GAP permutation groups act from the right. When applying the group that is output by this function this difference has to be kept in mind. For example, the orbit of a root b under W equals the set of images of b under the representatives of the left cosets of the stabilizer of b. But when we use the group G we have to consider the right cosets for this. Example gap> R:= RootSystem("E",6); <root system of type E6> gap> G:= WeylGroupAsPermGroup( R ); <permutation group with 6 generators> gap> Size(G); 51840 2.2.4 ApplyWeylPermToWeight . ApplyWeylPermToWeight(R, p, w) (operation) Here R is a root system, p is an element of the group returned by WeylGroupAsPermGroup (2.2.3) with input R. Here w is a weight, that the list of coefficients of a weight when written as a linear combination of fundamental weights. This function returns the result of acting with the element of the Weyl group corresponding to p on w. Example gap> R:= RootSystem("D",4);; gap> G:= WeylGroupAsPermGroup(R); <permutation group with 4 generators> gap> wt:= ApplyWeylPermToWeight( R, Random(G), [1,1,1,1] );; gap> ConjugateDominantWeight( WeylGroup(R), wt ); [ 1, 1, 1, 1 ] 2.2.5 WeylWordAsPerm . WeylWordAsPerm(R, u) (operation) Here R is a root system, and u is an element of the Weyl group given as a (not necessarily reduced) word, that is, u is given by a list of indices between 1 and the rank of R. This function returns the permutation corresponding to u, that is, the image of u under the anti-iromorphism discussed in WeylGroupAsPermGroup (2.2.3). SLA 8 Example gap> R:= RootSystem("D",4);; gap> WeylWordAsPerm( R, [1,2,1,3,4,2,3,4,1] ); (1,23,12,17)(2,10,14,22)(3,19,16,6)(4,18,15,7)(5,13,11,24)(8,21)(9,20) 2.2.6 PermAsWeylWord .
Load more

Recommended publications
  • Affine Springer Fibers and Affine Deligne-Lusztig Varieties
    Affine Springer Fibers and Affine Deligne-Lusztig Varieties Ulrich G¨ortz Abstract. We give a survey on the notion of affine Grassmannian, on affine Springer fibers and the purity conjecture of Goresky, Kottwitz, and MacPher- son, and on affine Deligne-Lusztig varieties and results about their dimensions in the hyperspecial and Iwahori cases. Mathematics Subject Classification (2000). 22E67; 20G25; 14G35. Keywords. Affine Grassmannian; affine Springer fibers; affine Deligne-Lusztig varieties. 1. Introduction These notes are based on the lectures I gave at the Workshop on Affine Flag Man- ifolds and Principal Bundles which took place in Berlin in September 2008. There are three chapters, corresponding to the main topics of the course. The first one is the construction of the affine Grassmannian and the affine flag variety, which are the ambient spaces of the varieties considered afterwards. In the following chapter we look at affine Springer fibers. They were first investigated in 1988 by Kazhdan and Lusztig [41], and played a prominent role in the recent work about the “fun- damental lemma”, culminating in the proof of the latter by Ngˆo. See Section 3.8. Finally, we study affine Deligne-Lusztig varieties, a “σ-linear variant” of affine Springer fibers over fields of positive characteristic, σ denoting the Frobenius au- tomorphism. The term “affine Deligne-Lusztig variety” was coined by Rapoport who first considered the variety structure on these sets. The sets themselves appear implicitly already much earlier in the study of twisted orbital integrals. We remark that the term “affine” in both cases is not related to the varieties in question being affine, but rather refers to the fact that these are notions defined in the context of an affine root system.
    [Show full text]
  • Lie Algebras and Representation Theory Andreasˇcap
    Lie Algebras and Representation Theory Fall Term 2016/17 Andreas Capˇ Institut fur¨ Mathematik, Universitat¨ Wien, Nordbergstr. 15, 1090 Wien E-mail address: [email protected] Contents Preface v Chapter 1. Background 1 Group actions and group representations 1 Passing to the Lie algebra 5 A primer on the Lie group { Lie algebra correspondence 8 Chapter 2. General theory of Lie algebras 13 Basic classes of Lie algebras 13 Representations and the Killing Form 21 Some basic results on semisimple Lie algebras 29 Chapter 3. Structure theory of complex semisimple Lie algebras 35 Cartan subalgebras 35 The root system of a complex semisimple Lie algebra 40 The classification of root systems and complex simple Lie algebras 54 Chapter 4. Representation theory of complex semisimple Lie algebras 59 The theorem of the highest weight 59 Some multilinear algebra 63 Existence of irreducible representations 67 The universal enveloping algebra and Verma modules 72 Chapter 5. Tools for dealing with finite dimensional representations 79 Decomposing representations 79 Formulae for multiplicities, characters, and dimensions 83 Young symmetrizers and Weyl's construction 88 Bibliography 93 Index 95 iii Preface The aim of this course is to develop the basic general theory of Lie algebras to give a first insight into the basics of the structure theory and representation theory of semisimple Lie algebras. A problem one meets right in the beginning of such a course is to motivate the notion of a Lie algebra and to indicate the importance of representation theory. The simplest possible approach would be to require that students have the necessary background from differential geometry, present the correspondence between Lie groups and Lie algebras, and then move to the study of Lie algebras, which are easier to understand than the Lie groups themselves.
    [Show full text]
  • Note on the Decomposition of Semisimple Lie Algebras
    Note on the Decomposition of Semisimple Lie Algebras Thomas B. Mieling (Dated: January 5, 2018) Presupposing two criteria by Cartan, it is shown that every semisimple Lie algebra of finite dimension over C is a direct sum of simple Lie algebras. Definition 1 (Simple Lie Algebra). A Lie algebra g is Proposition 2. Let g be a finite dimensional semisimple called simple if g is not abelian and if g itself and f0g are Lie algebra over C and a ⊆ g an ideal. Then g = a ⊕ a? the only ideals in g. where the orthogonal complement is defined with respect to the Killing form K. Furthermore, the restriction of Definition 2 (Semisimple Lie Algebra). A Lie algebra g the Killing form to either a or a? is non-degenerate. is called semisimple if the only abelian ideal in g is f0g. Proof. a? is an ideal since for x 2 a?; y 2 a and z 2 g Definition 3 (Derived Series). Let g be a Lie Algebra. it holds that K([x; z; ]; y) = K(x; [z; y]) = 0 since a is an The derived series is the sequence of subalgebras defined ideal. Thus [a; g] ⊆ a. recursively by D0g := g and Dn+1g := [Dng;Dng]. Since both a and a? are ideals, so is their intersection Definition 4 (Solvable Lie Algebra). A Lie algebra g i = a \ a?. We show that i = f0g. Let x; yi. Then is called solvable if its derived series terminates in the clearly K(x; y) = 0 for x 2 i and y = D1i, so i is solv- trivial subalgebra, i.e.
    [Show full text]
  • Matrix Lie Groups
    Maths Seminar 2007 MATRIX LIE GROUPS Claudiu C Remsing Dept of Mathematics (Pure and Applied) Rhodes University Grahamstown 6140 26 September 2007 RhodesUniv CCR 0 Maths Seminar 2007 TALK OUTLINE 1. What is a matrix Lie group ? 2. Matrices revisited. 3. Examples of matrix Lie groups. 4. Matrix Lie algebras. 5. A glimpse at elementary Lie theory. 6. Life beyond elementary Lie theory. RhodesUniv CCR 1 Maths Seminar 2007 1. What is a matrix Lie group ? Matrix Lie groups are groups of invertible • matrices that have desirable geometric features. So matrix Lie groups are simultaneously algebraic and geometric objects. Matrix Lie groups naturally arise in • – geometry (classical, algebraic, differential) – complex analyis – differential equations – Fourier analysis – algebra (group theory, ring theory) – number theory – combinatorics. RhodesUniv CCR 2 Maths Seminar 2007 Matrix Lie groups are encountered in many • applications in – physics (geometric mechanics, quantum con- trol) – engineering (motion control, robotics) – computational chemistry (molecular mo- tion) – computer science (computer animation, computer vision, quantum computation). “It turns out that matrix [Lie] groups • pop up in virtually any investigation of objects with symmetries, such as molecules in chemistry, particles in physics, and projective spaces in geometry”. (K. Tapp, 2005) RhodesUniv CCR 3 Maths Seminar 2007 EXAMPLE 1 : The Euclidean group E (2). • E (2) = F : R2 R2 F is an isometry . → | n o The vector space R2 is equipped with the standard Euclidean structure (the “dot product”) x y = x y + x y (x, y R2), • 1 1 2 2 ∈ hence with the Euclidean distance d (x, y) = (y x) (y x) (x, y R2).
    [Show full text]
  • Lecture 5: Semisimple Lie Algebras Over C
    LECTURE 5: SEMISIMPLE LIE ALGEBRAS OVER C IVAN LOSEV Introduction In this lecture I will explain the classification of finite dimensional semisimple Lie alge- bras over C. Semisimple Lie algebras are defined similarly to semisimple finite dimensional associative algebras but are far more interesting and rich. The classification reduces to that of simple Lie algebras (i.e., Lie algebras with non-zero bracket and no proper ideals). The classification (initially due to Cartan and Killing) is basically in three steps. 1) Using the structure theory of simple Lie algebras, produce a combinatorial datum, the root system. 2) Study root systems combinatorially arriving at equivalent data (Cartan matrix/ Dynkin diagram). 3) Given a Cartan matrix, produce a simple Lie algebra by generators and relations. In this lecture, we will cover the first two steps. The third step will be carried in Lecture 6. 1. Semisimple Lie algebras Our base field is C (we could use an arbitrary algebraically closed field of characteristic 0). 1.1. Criteria for semisimplicity. We are going to define the notion of a semisimple Lie algebra and give some criteria for semisimplicity. This turns out to be very similar to the case of semisimple associative algebras (although the proofs are much harder). Let g be a finite dimensional Lie algebra. Definition 1.1. We say that g is simple, if g has no proper ideals and dim g > 1 (so we exclude the one-dimensional abelian Lie algebra). We say that g is semisimple if it is the direct sum of simple algebras. Any semisimple algebra g is the Lie algebra of an algebraic group, we can take the au- tomorphism group Aut(g).
    [Show full text]
  • Holomorphic Diffeomorphisms of Complex Semisimple Lie Groups
    HOLOMORPHIC DIFFEOMORPHISMS OF COMPLEX SEMISIMPLE LIE GROUPS ARPAD TOTH AND DROR VAROLIN 1. Introduction In this paper we study the group of holomorphic diffeomorphisms of a complex semisimple Lie group. These holomorphic diffeomorphism groups are infinite di- mensional. To get additional information on these groups, we consider, for instance, the following basic problem: Given a complex semisimple Lie group G, a holomor- phic vector field X on G, and a compact subset K ⊂⊂ G, the flow of X, when restricted to K, is defined up to some nonzero time, and gives a biholomorphic map from K onto its image. When can one approximate this map uniformly on K by a global holomorphic diffeomorphism of G? One condition on a complex manifold which guarantees a positive solution of this problem, and which is possibly equiva- lent to it, is the so called density property, to be defined shortly. The main result of this paper is the following Theorem Every complex semisimple Lie group has the density property. Let M be a complex manifold and XO(M) the Lie algebra of holomorphic vector fields on M. Recall [V1] that a complex manifold is said to have the density property if the Lie subalgebra of XO(M) generated by its complete vector fields is a dense subalgebra. See section 2 for the definition of completeness. Since XO(M) is extremely large when M is Stein, the density property is particularly nontrivial in this case. One of the two main tools underlying the proof of our theorem is the general notion of shears and overshears, introduced in [V3].
    [Show full text]
  • Note to Users
    NOTE TO USERS This reproduction is the best copy available. The Rigidity Method and Applications Ian Stewart, Department of hIathematics McGill University, Montréal h thesis çubrnitted to the Faculty of Graduate Studies and Research in partial fulfilrnent of the requirements of the degree of MSc. @[an Stewart. 1999 National Library Bibliothèque nationale 1*1 0fC-& du Canada Acquisitions and Acquisilions et Bibliographie Services services bibliographiques 385 Wellington &eet 395. nie Weüington ôuawa ON KlA ON4 mwaON KlAW Canada Canada The author has granted a non- L'auteur a accordé une Licence non exclusive licence aiiowing the exclusive pennettant à la National Lïbrary of Canada to Brbhothèque nationale du Canada de reproduce, Ioan, distri'bute or sell reproduire, prêter, distribuer ou copies of this thesis m microform, vendre des copies de cette thèse sous paper or electronic formats. la forme de microfiche/filnl de reproduction sur papier ou sur format éIectronique. The author retains ownership of the L'auteur conserve la propriété du copyright in this thesis. Neither the droit d'auteur qui protège cette thèse. thesis nor substantial extracts fiom it Ni la thèse ni des extraits substantiels may be printed or otherwise de ceiie-ci ne doivent être imprimés reproduced without the author's ou autrement reproduits sans son permission. autorisation. Abstract The Inverse Problem ol Gnlois Thcor? is (liscuss~~l.In a spticifiç forni. the problem asks tr-hether ewry finitr gruiip occurs aç a Galois groiip over Q. An iritrinsically group theoretic property caIIed rigidity is tlcscribed which confirnis chat many simple groups are Galois groups ovrr Q.
    [Show full text]
  • Contents 1 Root Systems
    Stefan Dawydiak February 19, 2021 Marginalia about roots These notes are an attempt to maintain a overview collection of facts about and relationships between some situations in which root systems and root data appear. They also serve to track some common identifications and choices. The references include some helpful lecture notes with more examples. The author of these notes learned this material from courses taught by Zinovy Reichstein, Joel Kam- nitzer, James Arthur, and Florian Herzig, as well as many student talks, and lecture notes by Ivan Loseu. These notes are simply collected marginalia for those references. Any errors introduced, especially of viewpoint, are the author's own. The author of these notes would be grateful for their communication to [email protected]. Contents 1 Root systems 1 1.1 Root space decomposition . .2 1.2 Roots, coroots, and reflections . .3 1.2.1 Abstract root systems . .7 1.2.2 Coroots, fundamental weights and Cartan matrices . .7 1.2.3 Roots vs weights . .9 1.2.4 Roots at the group level . .9 1.3 The Weyl group . 10 1.3.1 Weyl Chambers . 11 1.3.2 The Weyl group as a subquotient for compact Lie groups . 13 1.3.3 The Weyl group as a subquotient for noncompact Lie groups . 13 2 Root data 16 2.1 Root data . 16 2.2 The Langlands dual group . 17 2.3 The flag variety . 18 2.3.1 Bruhat decomposition revisited . 18 2.3.2 Schubert cells . 19 3 Adelic groups 20 3.1 Weyl sets . 20 References 21 1 Root systems The following examples are taken mostly from [8] where they are stated without most of the calculations.
    [Show full text]
  • Introduction to Affine Grassmannians
    Introduction to Affine Grassmannians Sara Billey University of Washington http://www.math.washington.edu/∼billey Connections for Women: Algebraic Geometry and Related Fields January 23, 2009 0-0 Philosophy “Combinatorics is the equivalent of nanotechnology in mathematics.” 0-1 Outline 1. Background and history of Grassmannians 2. Schur functions 3. Background and history of Affine Grassmannians 4. Strong Schur functions and k-Schur functions 5. The Big Picture New results based on joint work with • Steve Mitchell (University of Washington) arXiv:0712.2871, 0803.3647 • Sami Assaf (MIT), preprint coming soon! 0-2 Enumerative Geometry Approximately 150 years ago. Grassmann, Schubert, Pieri, Giambelli, Severi, and others began the study of enumerative geometry. Early questions: • What is the dimension of the intersection between two general lines in R2? • How many lines intersect two given lines and a given point in R3? • How many lines intersect four given lines in R3 ? Modern questions: • How many points are in the intersection of 2,3,4,. Schubert varieties in general position? 0-3 Schubert Varieties A Schubert variety is a member of a family of projective varieties which is defined as the closure of some orbit under a group action in a homogeneous space G/H. Typical properties: • They are all Cohen-Macaulay, some are “mildly” singular. • They have a nice torus action with isolated fixed points. • This family of varieties and their fixed points are indexed by combinatorial objects; e.g. partitions, permutations, or Weyl group elements. 0-4 Schubert Varieties “Honey, Where are my Schubert varieties?” Typical contexts: • The Grassmannian Manifold, G(n, d) = GLn/P .
    [Show full text]
  • Special Unitary Group - Wikipedia
    Special unitary group - Wikipedia https://en.wikipedia.org/wiki/Special_unitary_group Special unitary group In mathematics, the special unitary group of degree n, denoted SU( n), is the Lie group of n×n unitary matrices with determinant 1. (More general unitary matrices may have complex determinants with absolute value 1, rather than real 1 in the special case.) The group operation is matrix multiplication. The special unitary group is a subgroup of the unitary group U( n), consisting of all n×n unitary matrices. As a compact classical group, U( n) is the group that preserves the standard inner product on Cn.[nb 1] It is itself a subgroup of the general linear group, SU( n) ⊂ U( n) ⊂ GL( n, C). The SU( n) groups find wide application in the Standard Model of particle physics, especially SU(2) in the electroweak interaction and SU(3) in quantum chromodynamics.[1] The simplest case, SU(1) , is the trivial group, having only a single element. The group SU(2) is isomorphic to the group of quaternions of norm 1, and is thus diffeomorphic to the 3-sphere. Since unit quaternions can be used to represent rotations in 3-dimensional space (up to sign), there is a surjective homomorphism from SU(2) to the rotation group SO(3) whose kernel is {+ I, − I}. [nb 2] SU(2) is also identical to one of the symmetry groups of spinors, Spin(3), that enables a spinor presentation of rotations. Contents Properties Lie algebra Fundamental representation Adjoint representation The group SU(2) Diffeomorphism with S 3 Isomorphism with unit quaternions Lie Algebra The group SU(3) Topology Representation theory Lie algebra Lie algebra structure Generalized special unitary group Example Important subgroups See also 1 of 10 2/22/2018, 8:54 PM Special unitary group - Wikipedia https://en.wikipedia.org/wiki/Special_unitary_group Remarks Notes References Properties The special unitary group SU( n) is a real Lie group (though not a complex Lie group).
    [Show full text]
  • Conjugacy Classes in the Weyl Group Compositio Mathematica, Tome 25, No 1 (1972), P
    COMPOSITIO MATHEMATICA R. W. CARTER Conjugacy classes in the weyl group Compositio Mathematica, tome 25, no 1 (1972), p. 1-59 <http://www.numdam.org/item?id=CM_1972__25_1_1_0> © Foundation Compositio Mathematica, 1972, tous droits réservés. L’accès aux archives de la revue « Compositio Mathematica » (http: //http://www.compositio.nl/) implique l’accord avec les conditions géné- rales d’utilisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou impression systématique est constitutive d’une infrac- tion pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ COMPOSITIO MATHEMATICA, Vol. 25, Fasc. 1, 1972, pag. 1-59 Wolters-Noordhoff Publishing Printed in the Netherlands CONJUGACY CLASSES IN THE WEYL GROUP by R. W. Carter 1. Introduction The object of this paper is to describe the decomposition of the Weyl group of a simple Lie algebra into its classes of conjugate elements. By the Cartan-Killing classification of simple Lie algebras over the complex field [7] the Weyl groups to be considered are: Now the conjugacy classes of all these groups have been determined individually, in fact it is also known how to find the irreducible complex characters of all these groups. W(AI) is isomorphic to the symmetric group 8z+ l’ Its conjugacy classes are parametrised by partitions of 1+ 1 and its irreducible representations are obtained by the classical theory of Frobenius [6], Schur [9] and Young [14]. W(B,) and W (Cl) are both isomorphic to the ’hyperoctahedral group’ of order 2’.l! Its conjugacy classes can be parametrised by pairs of partitions (À, Il) with JÂJ + Lui = 1, and its irreducible representations have been described by Specht [10] and Young [15].
    [Show full text]
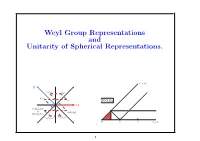
  • Weyl Group Representations and Unitarity of Spherical Representations
    Weyl Group Representations and Unitarity of Spherical Representations. Alessandra Pantano, University of California, Irvine Windsor, October 23, 2008 ν1 = ν2 β S S ν α β Sβν Sαν ν SO(3,2) 0 α SαSβSαSβν = SβSαSβν SβSαSβSαν S S SαSβSαν β αν 0 1 2 ν = 0 [type B2] 2 1 0: Introduction Spherical unitary dual of real split semisimple Lie groups spherical equivalence classes of unitary-dual = irreducible unitary = ? of G spherical repr.s of G aim of the talk Show how to compute this set using the Weyl group 2 0: Introduction Plan of the talk ² Preliminary notions: root system of a split real Lie group ² De¯ne the unitary dual ² Examples (¯nite and compact groups) ² Spherical unitary dual of non-compact groups ² Petite K-types ² Real and p-adic groups: a comparison of unitary duals ² The example of Sp(4) ² Conclusions 3 1: Preliminary Notions Lie groups Lie Groups A Lie group G is a group with a smooth manifold structure, such that the product and the inversion are smooth maps Examples: ² the symmetryc group Sn=fbijections on f1; 2; : : : ; ngg à finite ² the unit circle S1 = fz 2 C: kzk = 1g à compact ² SL(2; R)=fA 2 M(2; R): det A = 1g à non-compact 4 1: Preliminary Notions Root systems Root Systems Let V ' Rn and let h; i be an inner product on V . If v 2 V -f0g, let hv;wi σv : w 7! w ¡ 2 hv;vi v be the reflection through the plane perpendicular to v. A root system for V is a ¯nite subset R of V such that ² R spans V , and 0 2= R ² if ® 2 R, then §® are the only multiples of ® in R h®;¯i ² if ®; ¯ 2 R, then 2 h®;®i 2 Z ² if ®; ¯ 2 R, then σ®(¯) 2 R A1xA1 A2 B2 C2 G2 5 1: Preliminary Notions Root systems Simple roots Let V be an n-dim.l vector space and let R be a root system for V .
    [Show full text]