STAD29 / STA 1007 Assignment 8
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

— 2010 T&FN Men's World Rankings —
— 2010 T&FN Men’s World Rankings — 100 METERS 1500 METERS 110 HURDLES 1. Tyson Gay (US) 1. Asbel Kiprop (Kenya) 1. David Oliver (US) 2. Usain Bolt (Jamaica) 2. Amine Laâlou (Morocco) 2. Dayron Robles (Cuba) 3. Asafa Powell (Jamaica) 3. Silas Kiplagat (Kenya) 3. Dwight Thomas (Jamaica) 4. Nesta Carter (Jamaica) 4. Augustine Choge (Kenya) 4. Ryan Wilson (US) 5. Yohan Blake (Jamaica) 5. Mekonnen Gebremedhin (Ethiopia) 5. Ronnie Ash (US) 6. Richard Thompson (Trinidad) 6. Leonel Manzano (US) 6. Joel Brown (US) 7. Daniel Bailey (Antigua) 7. Nicholas Kemboi (Kenya) 7. Andy Turner (Great Britain) 8. Michael Frater (Jamaica) 8. Daniel Komen (Kenya) 8. David Payne (US) 9. Mike Rodgers (US) 9. Andrew Wheating (US) 9. Petr Svoboda (Czech Republic) 10. Christophe Lemaitre (France) 10. Ryan Gregson (Australia) 10. Garfield Darien (France) 200 METERS STEEPLECHASE 400 HURDLES 1. Walter Dix (US) 1. Paul Koech II (Kenya) 1. Bershawn Jackson (US) 2. Wallace Spearmon (US) 2. Ezekiel Kemboi (Kenya) 2. Kerron Clement (US) 3. Usain Bolt (Jamaica) 3. Richard Matelong (Kenya) 3. Javier Culson (Puerto Rico) 4. Tyson Gay (US) 4. Brimin Kipruto (Kenya) 4. Dai Greene (Great Britain) 5. Yohan Blake (Jamaica) 5. Benjamin Kiplagat (Uganda) 5. Angelo Taylor (US) 6. Ryan Bailey (US) 6. Mahiedine 6. Johnny Dutch (US) 7. Steve Mullings (Jamaica) Mekhissi-Benabbad (France) 7. Justin Gaymon (US) 8. Xavier Carter (US) 7. Roba Gari (Ethiopia) 8. Félix Sánchez (Dominican Rep) 9. Angelo Taylor (US) 8. Bob Tahri (France) 9. LJ van Zyl (South Africa) 10. Churandy Martina 9. Patrick Langat (Kenya) 10. Isa Phillips (Jamaica) (Netherlands Antilles) 10. -

23.12.2011 7 Kg; 107 Cm; 2 Kg; 800 G 20110109 Campbelltown 1137 00 673 +25 1326 193 4946 1553 00 3397 460 5463 44563 1 Jarrod Si
23.12.2011 7 kg; 107 cm; 2 kg; 800 g 20110109 Campbelltown 1 Jarrod Sims 7215 1137 00 673 +25 132619349461553 00 3397460546344563 20110213 Tauranga 1 Brent Newdick 7296 1132 +01 701 00 134518951101547 -07 4329440530944763 2 Scott McLaren 7036 1162 +01 678 00 138318650601612 -07 3857450527045017 20110217 Qatif 1 Mohamed Ridha Al-Matroud 6864 1118 -04 692 130817550381528 -07 3866390510950232 20110227 Melbourne 1 Stephen Cain 7416 1143 00 676 +16 133019350511522 -06 3737480556443375 2 Jarrod Sims 7155 1126 00 670 -05 128119649561587 -06 3731440515544478 20110317 Houston 1 Jon Ryan Harlan 7720 1122 -11 680 -04 149819950901455 +07 4325490610750791 20110318 La Habana 1 Jose Angel Mendieta Errasti 7404 1122 -18 730 00 153619252171462 -13 3780400633850629 2 Juan Gilberto Alcazar Oquendo 7200 1166 -18 696 +18 117919851721553 -13 3866440545242913 3 Danilo Rey Batista 7078 1137 -18 697 00 113218650061492 -13 3841360597243676 4 Manuel Gonzalez 6817 1188 -18 667 +05 140019553121597 -13 3891380519443886 20110318 Northridge 1 Benjamin Dillow 7145 1142 +29 646 +18 123818951091525 +09 4249435517343319 20110318 San Diego 1 Derek Steinbach 6801 1148 628 +09 133418654281564 +01 4069435563650187 20110320 Sao Paulo 1 Carlos Eduardo Bezerra Chinin 7581 1121 -33 758 +21 134320249601470 -39 3892440549750304 2 Danilo Mendes Xavier 7217 1140 -33 735 +23 133519051211531 -39 3884420571850000 3 Renato Atila Souza da Camara 7117 1166 -07 725 +47 132319652101527 -39 4160440487750327 20110325 San Angelo 1 Brent Vogel 7238 W 1116 +41 688 +53 117718648991495 +19 3775405554543395 -
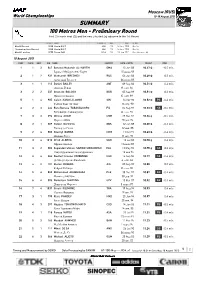
SUMMARY 100 Metres Men - Preliminary Round First 2 in Each Heat (Q) and the Next 3 Fastest (Q) Advance to the 1St Round
Moscow (RUS) World Championships 10-18 August 2013 SUMMARY 100 Metres Men - Preliminary Round First 2 in each heat (Q) and the next 3 fastest (q) advance to the 1st Round RESULT NAME COUNTRY AGE DATE VENUE World Record 9.58 Usain BOLT JAM 23 16 Aug 2009 Berlin Championships Record 9.58 Usain BOLT JAM 23 16 Aug 2009 Berlin World Leading 9.75 Tyson GAY USA 31 21 Jun 2013 Des Moines, IA 10 August 2013 RANK PLACE HEAT BIB NAME COUNTRY DATE of BIRTH RESULT WIND 1 1 3 847 Barakat Mubarak AL-HARTHI OMA 15 Jun 88 10.47 Q -0.5 m/s Баракат Мубарак Аль -Харти 15 июня 88 2 1 2 932 Aleksandr BREDNEV RUS 06 Jun 88 10.49 Q 0.3 m/s Александр Бреднев 06 июня 88 3 1 1 113Daniel BAILEY ANT 09 Sep 86 10.51 Q -0.4 m/s Даниэль Бэйли 09 сент . 86 3 2 2 237Innocent BOLOGO BUR 05 Sep 89 10.51 Q 0.3 m/s Инносент Болого 05 сент . 89 5 1 4 985 Calvin KANG LI LOONG SIN 16 Apr 90 10.52 Q PB -0.4 m/s Кэлвин Канг Ли Лонг 16 апр . 90 6 2 3 434 Ratu Banuve TABAKAUCORO FIJ 04 Sep 92 10.53 Q SB -0.5 m/s Рату Бануве Табакаукоро 04 сент . 92 7 3 3 296Idrissa ADAM CMR 28 Dec 84 10.56 q -0.5 m/s Идрисса A дам 28 дек . 84 8 2 1 509Holder DA SILVA GBS 12 Jan 88 10.59 Q -0.4 m/s Холдер да Силва 12 янв . -

IAAF World Indoor Championships 2012 Istanbul (TUR) - Frida�, Mar 09, 2012 High Jump - W QUALIFICATION Qual
------------------------------------------------------------------------------------- IAAF World Indoor Championships 2012 Istanbul (TUR) - Friday, Mar 09, 2012 High Jump - W QUALIFICATION Qual. rule: qualification standard 1.95m or at least best 8 qualified. ------------------------------------------------------------------------------------- Group A 09 March 2012 - 9:30 Position Bib Athlete Country Mark . 1 722 Anna Chicherova RUS 1.95 Q . 1 758 Ebba Jungmark SWE 1.95 Q (SB) 3 639 Antonietta Di Martino ITA 1.95 Q (SB) 3 807 Chaunté Lowe USA 1.95 Q . 5 832 Svetlana Radzivil UZB 1.95 Q (SB) 6 514 Tia Hellebaut BEL 1.95 Q . 7 576 Ruth Beitia ESP 1.92 q . 7 712 Esthera Petre ROU 1.92 q . 9 668 Airiné Palšyté LTU 1.92 (SB) 9 727 Irina Gordeeva RUS 1.92 . 9 756 Emma Green Tregaro SWE 1.92 . 12 582 Anna Iljuštšenko EST 1.88 . 13 558 Xingjuan Zheng CHN 1.88 . 14 564 Ana Šimic CRO 1.88 . 15 666 Levern Spencer LCA 1.88 (SB) 15 692 Tonje Angelsen NOR 1.88 . 17 782 Oksana Okuneva UKR 1.83 . 18 652 Marina Aitova KAZ 1.83 . 547 Venelina Veneva-Mateeva BUL NM . 814 Inika McPherson USA NM . 766 Burcu Ayhan TUR DNS . Athlete 1.78 1.83 1.88 1.92 1.95 Anna Chicherova - O O O O Ebba Jungmark - O O O O Antonietta Di Martino - O O O XO Chaunté Lowe O O O O XO Svetlana Radzivil O O O XXO XO Tia Hellebaut O XO O XXO XO Ruth Beitia - O O O XXX Esthera Petre O O O O XXX Airiné Palšyté O O O XO XXX Irina Gordeeva - O O XO XXX Emma Green Tregaro - O O XO XXX Anna Iljuštšenko O O O XXX Xingjuan Zheng O O XO XXX Ana Šimic O XXO XO XXX Levern Spencer O O XXO XXX Tonje Angelsen O O XXO XXX Oksana Okuneva O XO XXX Marina Aitova O XXO XXX Venelina Veneva-Mateeva - XXX Inika McPherson XXX Burcu Ayhan ------------------------------------------------------------------------------------- IAAF World Indoor Championships 2012 Istanbul (TUR) - Friday, Mar 09, 2012 Triple Jump - W QUALIFICATION Qual. -

HARDEE's 8689 a CHAMPION at GOTZIS Smith Is NACAC Winner
Volume XXXVI Number 29 May (6), 2011 HARDEE’s 8689 a CHAMPION at GOTZIS Smith is NACAC Winner Hello Again….The final weekend in May came to a close on Saturday evening in Kingston, Jamacia with Maurice Smith‟s NACAC victory and on Sunday afternoon at Mösle Stadium in Götzis Austria where Trey Hardee maintained his hot pace and pasted a terrific 27 man field by a whopping 249 points. Hardee‟s final tally of 8689 is his 2nd best career score,101 down on his 8790 PR set at the ‟09 IAAF worlds in Berlin (see box). Here‟s the story: 37th Hypo-Bank Meeting Mosle Stadium Götzis, Austria May 28-29, 2011 110m Hurdles: [10:05 am] The weather was even better on day 2, clear, brisk, and 70 degrees at race time. Trey Hardee, 27, Austin, TX, manhandled the Götzis field with a season opening 8689 score. Götzis church bells gonged as the athletes in the first race went to their starting blocks. meet as he won by 4 steps over Rico Freimuth Young Austrian Dominic Distelberger (14.05) whose father Uwe (part of the East nd won the first section of four in 14.28. The 2 German team) won the first Götzis race resembled a German intra-squad meet meet I attended, in 1988. Approximately 1000 but was captured by Thomas Van Der spectators were on hand for the 1st event. Plaetsen of Belgium in 14.65. Oleksiy After Six: Hard 5563, Kasy 5231, Frie 5132, Kasyanov/UKR (14.26) beat Cuba‟s Leonel Garc 5082……Arno 4625. -

Dossier De Presse
DOSSIER DE PRESSE Communication et partenariat : Nicole DURAND 06 71 23 37 83 Presse : Nicole DURAND - Charles FOULGOT 06 07 16 64 59 Secrétariat : 05 56 04 39 36 - [email protected] 1 I.LE DECASTAR Présentation p. 3 Au fil des ans p. 4 Le palmarès p. 7 Les records du décathlon et de l'heptathlon p. 8 Les records du stade p. 9 L’année 2018 des épreuves combinées p. 10 Les derniers championnats p.12 Décastar 2018 : les engagés p.13 Le Décastar en chiffres p.14 Les horaires p.15 L’accès au stade et les tarifs p.17 Le plan d’accès au stade p.18 II.L’ADEM (Association pour le Développement des Epreuves combinées et du Meeting de Talence) Une passion au service du sport p.19 Le collège d'athlètes p.20 Les partenaires p.21 III.ANNEXES Accréditation (formulaire de demande) p.22 Biographies des athlètes p.23 L’Equipe de France en mode Décastar p.31 2 I.LE DECASTAR De l’INSEP à Talence… L’histoire du Décastar débuta lors d’un déjeuner, en 1974, au restaurant de l’INSEP à Paris entre Christian DENIS, alors responsable national des épreuves combinées, et Pierre DARRIERE, entraîneur national, quand ils imaginèrent la création d’une compétition internationale initialement prévue dans la région parisienne, et finalement lancée à Talence par Louis SENILLON et le comité de Gironde, avec le soutien de Gérard CASTAGNERA et de la municipalité. Les 4 et 5 septembre 1976, Guy DRUT, champion olympique du 110 m haies le 28 juillet à Montréal, avait attiré plus de dix mille spectateurs, cinquante journalistes et Antenne 2 en direct pour un défi un peu fou. -

Men's Decathlon
World Rankings — Men’s Decathlon Ashton Eaton’s © VICTOR SAILER/PHOTO RUN fabulous No. 1 season of 2012 included Olympic gold and the World Record 1947 1949 1 ............ Vladimir Volkov (Soviet Union) 1 .................................. Bob Mathias (US) 2 .................... Heino Lipp (Soviet Union) 2 .................... Heino Lipp (Soviet Union) 3 .....................Erik Andersson (Sweden) 3 ...........................Örn Clausen (Iceland) 4 ...... Enrique Kistenmacher (Argentina) 4 ...................... Ignace Heinrich (France) 5 .................................. Al Lawrence (US) 5 ...........Pyotr Denisenko (Soviet Union) 6 ......Sergey Kuznyetsov (Soviet Union) 6 ........................ Moon Mondschein (US) 7 ......................... Per Eriksson (Sweden) 7 ............ Vladimir Volkov (Soviet Union) 8 ........................ Moon Mondschein (US) 8 .... Miloslav Moravec (Czechoslovakia) 9 ......................................Lloyd Duff (US) 9 ..............Armin Scheurer (Switzerland) 10 .................. Allan Svensson (Sweden) 10 .... Enrique Kistenmacher (Argentina) 1948 1950 1 .................... Heino Lipp (Soviet Union) 1 .................................. Bob Mathias (US) 2 .................................. Bob Mathias (US) 2 ..................................... Bill Albans (US) 3 ...................... Ignace Heinrich (France) 3 ...................... Ignace Heinrich (France) 4 .............................Floyd Simmons (US) 4 .................... Heino Lipp (Soviet Union) 5 ...... Enrique Kistenmacher (Argentina) -

23.12.2011 7 Kg
23.12.2011 7 kg; 107 cm; 2 kg; 800 g 8729 Ashton Eaton 2101 1988USA 1 20110624Eugene 1033+06 780 +31 1414 205 4635 1352+16 4158 505 5619 42410 8689 James Edward Hardee 0702 1984USA 1 20110529Götzis 1044 -07 788 +06 1563 200 4812 1373 00 4520 506 6333 44688 8501 Leonel Suarez Fiajardo 0109 1987CUB 3 20110828Daegu 1107 -02 733 1454 205 4917 1429 -07 4625 500 6912 42416 8398 Mikk Pahapill 1807 1983 EST 3 20110529Götzis 1108+09 739 -13 1548 203 5095 1470 -09 4879 506 6953 43941 8397 Yordani Garcia Barrizonte 2111 1988CUB 1 20110506La Habana 1086 00 700 00 1590 207 4915 1447+16 4522 480 6770 43140 8334 Aleksei Drozdov 0312 1983RUS 1 20110610Cheboksary 1128 -08 727 00 1631 212 5167 1498 00 5124 510 6382 44500 8312 Edgars Erinš 1806 1986 LAT 1 20110604Valmiera 1079+21 767 +02 1419 190 4865 1456+12 4994 450 5830 41425 8304 Eelco Sintnicolaas 0704 1987NED 4 20110529Götzis 1084+04 740 -09 1431 191 4869 1457 -09 4174 536 5948 42229 8302 Larbi Bouraada 1005 1988 ALG 1 20110717Ratingen 1061+34 794 +27 1282 206 4819 1465 -03 4034 470 5805 42142 8288 Jan Felix Knobel 1601 1989GER 5 20110529Götzis 1114 -08 723 +12 1547 194 4923 1477 -04 4668 496 7299 44339 (10) 8287 Rico Freimuth 1403 1988GER 2 20110717Ratingen 1050+34 742 +22 1444 188 4846 1414 -03 4742 480 6504 44944 8256 Mihail Dudaš 0111 1989SRB 6 20110828Daegu 1081 -05 741 +05 1376 202 4773 1489 -01 4397 490 5893 42606 8252 Olexiy Kasyanov 2608 1985UKR 6 20110529Götzis 1075 -07 738 +08 1408 203 4811 1426 -09 4694 476 5162 42712 8232 Pascal Behrenbruch 1901 1985GER 3 20110717Ratingen 1086+34 721 +19 -

Decathlon by K Ken Nakamura the Records to Look for in Tokyo: 1) by Winning a Medal, Both Warner and Mayer Become 14 Th Decathlete with Multiple Olympic Medals
2020 Olympic Games Statistics - Men’s Decathlon by K Ken Nakamura The records to look for in Tokyo: 1) By winning a medal, both Warner and Mayer become 14 th Decathlete with multiple Olympic medals. Warner or Mayer can become first CAN/FRA, respectively to win the Olympic Gold. 2) Can Maloney become first AUS to medal at the Olympic Games? Summary Page: All time Performance List at the Olympic Games Performance Performer Points Name Nat Pos Venue Yea r 1 1 8893 Roman Sebrle CZE 1 Athinai 2004 1 1 8893 Ashton Eaton USA 1 Rio de Janeiro 2016 3 8869 Ashton Eaton 1 London 2012 4 3 8834 Kevin Mayer FRA 2 Rio de Janeiro 2016 5 4 8824 Dan O’Brien USA 1 Atlanta 1996 6 5 8847/8798 Daley Thompson GBR 1 Los Angeles 1984 7 6 8820 Bryan Clay USA 2 Athinai 2004 Lowest winning score since 1976: 8488 by Christian Schenk (GDR) in 1988 Margin of Victory Difference Points Name Nat Venue Year Max 240 8791 Bryan Clay USA Beijing 2008 Min 35 8641 Erkki Nool EST Sydney 2000 Best Marks for Places in the Olympic Games Pos Points Name Nat Venue Year 1 8893 Roman Sebrle CZE Athinai 2004 Ashton Eaton USA Rio de Janeiro 2016 2 8834 Kevin Mayer FRA Rio de Janeiro 2016 8820 Bryan Clay USA Athinai 2004 3 8725 Dmitriy Karpov KAZ Athinai 2004 4 8644 Steve Fritz USA Atlanta 1996 Last eight Olympics: Year Gold Nat Time Silver Nat Time Bronze Nat Time 2016 Ashton Eaton USA 8893 Kevin Mayer FRA 8834 Damian Warner CAN 8666 2012 Ashton Eaton USA 8869 Trey Hardee USA 8671 Leonel Suarez CUB 8523 2008 Bryan Clay USA 8791 Andrey Kravcheko BLR 8551 Leonel Suarez CUB 8527 2004 Roman -

2019 World Championships Statistics
2019 World Championships Statistics - Men’s Decathlon by K Ken Nakamura The records likely to be broken in Doha: 1) Can Warner become first Pan American Games champion to win the World Championships? If he wins gold, he will be the first to have complete set of medals. Summary: All time Performance List at the World Championships Performance Performer Points Name Nat Pos Venue Year 1 1 9045 Ashton Eaton USA 1 Beijing 2015 2 2 8902 Tomas Dvorak CZE 1 Edmonton 2001 3 8837 Tomas Dvorak 1 Athinai 1997 4 3 8817 Dan O’Brien USA 1 St uttgart 1993 5 4 8815 Erki Nool EST 2 Edmonton 2001 6 8812 Dan O’Brien 1 Tokyo 1991 7 8809 Ashton Eaton 1 Moskva 2013 8 5 8790 Trey Hardee USA 1 Berlin 2009 9 6 8768 Kevin Mayer FRA 1 London 2017 10 7 8750 Tom Pappas USA 1 Paris 2003 Margin of Victory Difference Points Name Nat Venue Year Max 350 9045 Ashton Eaton USA Beijing 2015 263 8812 Dan O’Brien USA Tokyo 1991 219 8680 Torsten Voss GDR Roma 1987 Min 32 8676 Roman Sebrle CZE Osaka 2007 87 8902 Tomas Dvorak CZE Edmonton 2001 Best Marks for Places in the World Championships Pos Points Name Nat Venue Year 1 9045 Ashton Eaton USA Beijing 2015 8902 Tomas Dvorak CZE Edmonton 2001 2 8815 Erki Nool EST Edmonton 2001 8730 Eduard Hämäläinen FIN Athinai 1997 3 8652 Frank Busemann GER Athinai 1997 4 8538 Ilya Shkurenyov RUS Beijing 2015 8524 Sebastien Levicq FRA Sevilla 1999 World Championships medalist with Pan American Games gold medal Name Nat World Championships Year Pan American Games Damian Warner CAN Silver 2015 2015, 2019 Leonel Suarez CUB Silver 2009 2011 Maurice -

Le Décastar À Travers Le Temps
Le Décastar à travers le temps Le Décastar, meeting international d’Épreuves Combinées, accueille chaque année, sur le stade Pierre Paul Bernard de Talence, les meilleurs athlètes mondiaux de la discipline. Créé en 1976, il devient en 1991 le « Décastar, les Dieux du Stade ». En 1998 il est inscrit au challenge mondial des Epreuves Combinées, il en est la dernière étape. C’est après Talence que le classement final est établi, récompensant les 8 meilleurs du Décathlon et de l’Heptathlon. Théâtre d’inoubliables moments 1976 : première édition avec la participation de Guy DRUT, récent Champion Olympique du 110 m haies. Venu relever un défi sur un décathlon, il termine 5ème et établit le record du stade du 110 m haies, jamais égalé à ce jour. Fin des années 80, début des années 90 : 5 victoires de Christian PLAZIAT, n°1 mondial en 1987, 1988, 1989, multiple Champion, Recordman de France et Champion d’Europe à Split en 1990. 1992 : Le record du monde est battu par l’américain Dan O’BRIEN, triple Champion du Monde et Champion Olympique à Atlanta. 1994 : Venue de l’allemande Heike DRESCHLER, spécialiste du saut en longueur, qui réalise la meilleure performance mondiale de l’année. 1996 : 20ème anniversaire du DECASTAR, avec la participation de Jean GALFIONE, Champion Olympique à Atlanta. Il réalise la meilleure performance mondiale au saut à la perche dans un décathlon. 1999 : Eunice BARBER, Championne du Monde à Séoul, remporte le Challenge Mondial IAAF, après une victoire très disputée au DECASTAR. Tomas DVORAK, alors Recordman mondial, remporte la victoire au décathlon. -

EATON LEAPS to LEAD World Best 26-9½ Propels IAAF Charge
Volume XXXVII Number 14 March (3), 2012 EATON LEAPS to LEAD World Best 26-9½ Propels IAAF Charge Hello Again….. This will be the first of three (hopefully) world championship posts. The 9 hour time differential (b/w Istanbul and Boise, ID) will allow me, while announcing he NCAA D I meet, to pay attention to the world championship meet as well. Ashton Eaton is the lone American entrant in Istanbul, and, as the event’s world record holder, enters as the favorite. At 2:35 am (USA Mountain time) I found myself watching the Universal Sports streaming of the indoor worlds from Istanbul. The defining moment of the IAAF world indoor Eaton’s record long jump was the story. champs heptathlon was Ashton Eaton’s WR 8.16m/26-9½ long jump. Hello! the entire field. Eaton was away sluggishly (reaction time just 0.277- and only two were IAAF World Indoor T&F slower) but quickly eased away from the field Championships Men’s Heptathlon on the blue and grey infield and clocked a Istanbul, Turkey nifty 6.79 seconds (originally announced at March 9-10, 2012 6.78), .08 ahead of Kasyanov who was just .04 seconds shy of his own career Day One- Friday best. 60 meters: [11:35 am local time, 2:35 am USA Mountain time] Ashton Eaton drew lane 4 in a one race event with 8 athletes. Yet the race started 8 Results: lane time pts reaction 1. ..Ashton Eaton USA 4 6.79 958 0.277 minutes late and the internet provided 2.