Solid Geometry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Analytic Geometry
Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15 -

Arc Length. Surface Area
Calculus 2 Lia Vas Arc Length. Surface Area. Arc Length. Suppose that y = f(x) is a continuous function with a continuous derivative on [a; b]: The arc length L of f(x) for a ≤ x ≤ b can be obtained by integrating the length element ds from a to b: The length element ds on a sufficiently small interval can be approximated by the hypotenuse of a triangle with sides dx and dy: p Thus ds2 = dx2 + dy2 ) ds = dx2 + dy2 and so s s Z b Z b q Z b dy2 Z b dy2 L = ds = dx2 + dy2 = (1 + )dx2 = (1 + )dx: a a a dx2 a dx2 2 dy2 dy 0 2 Note that dx2 = dx = (y ) : So the formula for the arc length becomes Z b q L = 1 + (y0)2 dx: a Area of a surface of revolution. Suppose that y = f(x) is a continuous function with a continuous derivative on [a; b]: To compute the surface area Sx of the surface obtained by rotating f(x) about x-axis on [a; b]; we can integrate the surface area element dS which can be approximated as the product of the circumference 2πy of the circle with radius y and the height that is given by q the arc length element ds: Since ds is 1 + (y0)2dx; the formula that computes the surface area is Z b q 0 2 Sx = 2πy 1 + (y ) dx: a If y = f(x) is rotated about y-axis on [a; b]; then dS is the product of the circumference 2πx of the circle with radius x and the height that is given by the arc length element ds: Thus, the formula that computes the surface area is Z b q 0 2 Sy = 2πx 1 + (y ) dx: a Practice Problems. -

Geometry Around Us an Introduction to Non-Euclidean Geometry
Geometry Around Us An Introduction to Non-Euclidean Geometry Gaurish Korpal (gaurish4math.wordpress.com) National Institute of Science Education and Research, Bhubaneswar 23 April 2016 Science Day Celebration Gaurish Korpal(gaurish4math.wordpress.com) (NISER) Geometry Around Us 23 April 2016 1 / 15 Theorem In any triangle, trisector lines intersect at three points, that are vertices of an equilateral triangle. A. Bogomolny, Morley's Theorem: Proof by R. J. Webster, Interactive Mathematics Miscellany and Puzzle, http://www.cut-the-knot.org/triangle/Morley/Webster.shtml Morley's Miracle Frank Morley (USA) discovered a theorem about triangle in 1899, approximately 2000 years after first theorems about triangle were published by Euclid. Euclid (Egypt) is referred as father of Plane Geometry, often called Euclidean Geometry. Science Day Celebration Gaurish Korpal(gaurish4math.wordpress.com) (NISER) Geometry Around Us 23 April 2016 2 / 15 Morley's Miracle Frank Morley (USA) discovered a theorem about triangle in 1899, approximately 2000 years after first theorems about triangle were published by Euclid. Euclid (Egypt) is referred as father of Plane Geometry, often called Euclidean Geometry. Theorem In any triangle, trisector lines intersect at three points, that are vertices of an equilateral triangle. A. Bogomolny, Morley's Theorem: Proof by R. J. Webster, Interactive Mathematics Miscellany and Puzzle, http://www.cut-the-knot.org/triangle/Morley/Webster.shtml Science Day Celebration Gaurish Korpal(gaurish4math.wordpress.com) (NISER) Geometry Around Us 23 April 2016 2 / 15 Morley's original proof was (published in 1924) stemmed from his results on algebraic curves tangent to a given number of lines. It arose from the consideration of cardioids [(x 2 + y 2 − a2)2 = 4a2((x − a)2 + y 2)]. -
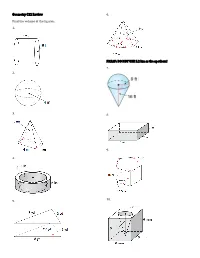
Geometry C12 Review Find the Volume of the Figures. 1. 2. 3. 4. 5. 6
Geometry C12 Review 6. Find the volume of the figures. 1. PREAP: DO NOT USE 5.2 km as the apothem! 7. 2. 3. 8. 9. 4. 10. 5. 11. 16. 17. 12. 18. 13. 14. 19. 15. 20. 21. A sphere has a volume of 7776π in3. What is the radius 33. Two prisms are similar. The ratio of their volumes is of the sphere? 8:27. The surface area of the smaller prism is 72 in2. Find the surface area of the larger prism. 22a. A sphere has a volume of 36π cm3. What is the radius and diameter of the sphere? 22b. A sphere has a volume of 45 ft3. What is the 34. The prisms are similar. approximate radius of the sphere? a. What is the scale factor? 23. The scale factor (ratio of sides) of two similar solids is b. What is the ratio of surface 3:7. What are the ratios of their surface areas and area? volumes? c. What is the ratio of volume? d. Find the volume of the 24. The scale factor of two similar solids is 12:5. What are smaller prism. the ratios of their surface areas and volumes? 35. The prisms are similar. 25. The scale factor of two similar solids is 6:11. What are a. What is the scale factor? the ratios of their surface areas and volumes? b. What is the ratio of surface area? 26. The ratio of the volumes of two similar solids is c. What is the ratio of 343:2197. What is the scale factor (ratio of sides)? volume? d. -

Cones, Pyramids and Spheres
The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 YEARS 910 Cones, Pyramids and Spheres (Measurement and Geometry : Module 12) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 910 {4} A guide for teachers CONES, PYRAMIDS AND SPHERES ASSUMED KNOWLEDGE • Familiarity with calculating the areas of the standard plane figures including circles. • Familiarity with calculating the volume of a prism and a cylinder. • Familiarity with calculating the surface area of a prism. • Facility with visualizing and sketching simple three‑dimensional shapes. • Facility with using Pythagoras’ theorem. • Facility with rounding numbers to a given number of decimal places or significant figures. -

Lateral and Surface Area of Right Prisms 1 Jorge Is Trying to Wrap a Present That Is in a Box Shaped As a Right Prism
CHAPTER 11 You will need Lateral and Surface • a ruler A • a calculator Area of Right Prisms c GOAL Calculate lateral area and surface area of right prisms. Learn about the Math A prism is a polyhedron (solid whose faces are polygons) whose bases are congruent and parallel. When trying to identify a right prism, ask yourself if this solid could have right prism been created by placing many congruent sheets of paper on prism that has bases aligned one above the top of each other. If so, this is a right prism. Some examples other and has lateral of right prisms are shown below. faces that are rectangles Triangular prism Rectangular prism The surface area of a right prism can be calculated using the following formula: SA 5 2B 1 hP, where B is the area of the base, h is the height of the prism, and P is the perimeter of the base. The lateral area of a figure is the area of the non-base faces lateral area only. When a prism has its bases facing up and down, the area of the non-base faces of a figure lateral area is the area of the vertical faces. (For a rectangular prism, any pair of opposite faces can be bases.) The lateral area of a right prism can be calculated by multiplying the perimeter of the base by the height of the prism. This is summarized by the formula: LA 5 hP. Copyright © 2009 by Nelson Education Ltd. Reproduction permitted for classrooms 11A Lateral and Surface Area of Right Prisms 1 Jorge is trying to wrap a present that is in a box shaped as a right prism. -

Analytic Geometry
STATISTIC ANALYTIC GEOMETRY SESSION 3 STATISTIC SESSION 3 Session 3 Analytic Geometry Geometry is all about shapes and their properties. If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres Point, Line, Plane and Solid A Point has no dimensions, only position A Line is one-dimensional A Plane is two dimensional (2D) A Solid is three-dimensional (3D) Plane Geometry Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). 2D Shapes Activity: Sorting Shapes Triangles Right Angled Triangles Interactive Triangles Quadrilaterals (Rhombus, Parallelogram, etc) Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite Interactive Quadrilaterals Shapes Freeplay Perimeter Area Area of Plane Shapes Area Calculation Tool Area of Polygon by Drawing Activity: Garden Area General Drawing Tool Polygons A Polygon is a 2-dimensional shape made of straight lines. Triangles and Rectangles are polygons. Here are some more: Pentagon Pentagra m Hexagon Properties of Regular Polygons Diagonals of Polygons Interactive Polygons The Circle Circle Pi Circle Sector and Segment Circle Area by Sectors Annulus Activity: Dropping a Coin onto a Grid Circle Theorems (Advanced Topic) Symbols There are many special symbols used in Geometry. Here is a short reference for you: -

Constructive Solid Geometry Concepts
3-1 Chapter 3 Constructive Solid Geometry Concepts Understand Constructive Solid Geometry Concepts Create a Binary Tree Understand the Basic Boolean Operations Use the SOLIDWORKS CommandManager User Interface Setup GRID and SNAP Intervals Understand the Importance of Order of Features Use the Different Extrusion Options 3-2 Parametric Modeling with SOLIDWORKS Certified SOLIDWORKS Associate Exam Objectives Coverage Sketch Entities – Lines, Rectangles, Circles, Arcs, Ellipses, Centerlines Objectives: Creating Sketch Entities. Rectangle Command ................................................3-10 Boss and Cut Features – Extrudes, Revolves, Sweeps, Lofts Objectives: Creating Basic Swept Features. Base Feature .............................................................3-9 Reverse Direction Option ........................................3-16 Hole Wizard ..............................................................3-20 Dimensions Objectives: Applying and Editing Smart Dimensions. Reposition Smart Dimension ..................................3-11 Feature Conditions – Start and End Objectives: Controlling Feature Start and End Conditions. Reference Guide Reference Extruded Cut, Up to Next .......................................3-25 Associate Certified Constructive Solid Geometry Concepts 3-3 Introduction In the 1980s, one of the main advancements in solid modeling was the development of the Constructive Solid Geometry (CSG) method. CSG describes the solid model as combinations of basic three-dimensional shapes (primitive solids). The -

Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Chapter 1: Analytic Geometry
1 Analytic Geometry Much of the mathematics in this chapter will be review for you. However, the examples will be oriented toward applications and so will take some thought. In the (x,y) coordinate system we normally write the x-axis horizontally, with positive numbers to the right of the origin, and the y-axis vertically, with positive numbers above the origin. That is, unless stated otherwise, we take “rightward” to be the positive x- direction and “upward” to be the positive y-direction. In a purely mathematical situation, we normally choose the same scale for the x- and y-axes. For example, the line joining the origin to the point (a,a) makes an angle of 45◦ with the x-axis (and also with the y-axis). In applications, often letters other than x and y are used, and often different scales are chosen in the horizontal and vertical directions. For example, suppose you drop something from a window, and you want to study how its height above the ground changes from second to second. It is natural to let the letter t denote the time (the number of seconds since the object was released) and to let the letter h denote the height. For each t (say, at one-second intervals) you have a corresponding height h. This information can be tabulated, and then plotted on the (t, h) coordinate plane, as shown in figure 1.0.1. We use the word “quadrant” for each of the four regions into which the plane is divided by the axes: the first quadrant is where points have both coordinates positive, or the “northeast” portion of the plot, and the second, third, and fourth quadrants are counted off counterclockwise, so the second quadrant is the northwest, the third is the southwest, and the fourth is the southeast. -

Hydraulics Manual Glossary G - 3
Glossary G - 1 GLOSSARY OF HIGHWAY-RELATED DRAINAGE TERMS (Reprinted from the 1999 edition of the American Association of State Highway and Transportation Officials Model Drainage Manual) G.1 Introduction This Glossary is divided into three parts: · Introduction, · Glossary, and · References. It is not intended that all the terms in this Glossary be rigorously accurate or complete. Realistically, this is impossible. Depending on the circumstance, a particular term may have several meanings; this can never change. The primary purpose of this Glossary is to define the terms found in the Highway Drainage Guidelines and Model Drainage Manual in a manner that makes them easier to interpret and understand. A lesser purpose is to provide a compendium of terms that will be useful for both the novice as well as the more experienced hydraulics engineer. This Glossary may also help those who are unfamiliar with highway drainage design to become more understanding and appreciative of this complex science as well as facilitate communication between the highway hydraulics engineer and others. Where readily available, the source of a definition has been referenced. For clarity or format purposes, cited definitions may have some additional verbiage contained in double brackets [ ]. Conversely, three “dots” (...) are used to indicate where some parts of a cited definition were eliminated. Also, as might be expected, different sources were found to use different hyphenation and terminology practices for the same words. Insignificant changes in this regard were made to some cited references and elsewhere to gain uniformity for the terms contained in this Glossary: as an example, “groundwater” vice “ground-water” or “ground water,” and “cross section area” vice “cross-sectional area.” Cited definitions were taken primarily from two sources: W.B.