The Simple Perceptron
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Training Autoencoders by Alternating Minimization
Under review as a conference paper at ICLR 2018 TRAINING AUTOENCODERS BY ALTERNATING MINI- MIZATION Anonymous authors Paper under double-blind review ABSTRACT We present DANTE, a novel method for training neural networks, in particular autoencoders, using the alternating minimization principle. DANTE provides a distinct perspective in lieu of traditional gradient-based backpropagation techniques commonly used to train deep networks. It utilizes an adaptation of quasi-convex optimization techniques to cast autoencoder training as a bi-quasi-convex optimiza- tion problem. We show that for autoencoder configurations with both differentiable (e.g. sigmoid) and non-differentiable (e.g. ReLU) activation functions, we can perform the alternations very effectively. DANTE effortlessly extends to networks with multiple hidden layers and varying network configurations. In experiments on standard datasets, autoencoders trained using the proposed method were found to be very promising and competitive to traditional backpropagation techniques, both in terms of quality of solution, as well as training speed. 1 INTRODUCTION For much of the recent march of deep learning, gradient-based backpropagation methods, e.g. Stochastic Gradient Descent (SGD) and its variants, have been the mainstay of practitioners. The use of these methods, especially on vast amounts of data, has led to unprecedented progress in several areas of artificial intelligence. On one hand, the intense focus on these techniques has led to an intimate understanding of hardware requirements and code optimizations needed to execute these routines on large datasets in a scalable manner. Today, myriad off-the-shelf and highly optimized packages exist that can churn reasonably large datasets on GPU architectures with relatively mild human involvement and little bootstrap effort. -

Q-Learning in Continuous State and Action Spaces
-Learning in Continuous Q State and Action Spaces Chris Gaskett, David Wettergreen, and Alexander Zelinsky Robotic Systems Laboratory Department of Systems Engineering Research School of Information Sciences and Engineering The Australian National University Canberra, ACT 0200 Australia [cg dsw alex]@syseng.anu.edu.au j j Abstract. -learning can be used to learn a control policy that max- imises a scalarQ reward through interaction with the environment. - learning is commonly applied to problems with discrete states and ac-Q tions. We describe a method suitable for control tasks which require con- tinuous actions, in response to continuous states. The system consists of a neural network coupled with a novel interpolator. Simulation results are presented for a non-holonomic control task. Advantage Learning, a variation of -learning, is shown enhance learning speed and reliability for this task.Q 1 Introduction Reinforcement learning systems learn by trial-and-error which actions are most valuable in which situations (states) [1]. Feedback is provided in the form of a scalar reward signal which may be delayed. The reward signal is defined in relation to the task to be achieved; reward is given when the system is successfully achieving the task. The value is updated incrementally with experience and is defined as a discounted sum of expected future reward. The learning systems choice of actions in response to states is called its policy. Reinforcement learning lies between the extremes of supervised learning, where the policy is taught by an expert, and unsupervised learning, where no feedback is given and the task is to find structure in data. -

Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting
water Article Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting Halit Apaydin 1 , Hajar Feizi 2 , Mohammad Taghi Sattari 1,2,* , Muslume Sevba Colak 1 , Shahaboddin Shamshirband 3,4,* and Kwok-Wing Chau 5 1 Department of Agricultural Engineering, Faculty of Agriculture, Ankara University, Ankara 06110, Turkey; [email protected] (H.A.); [email protected] (M.S.C.) 2 Department of Water Engineering, Agriculture Faculty, University of Tabriz, Tabriz 51666, Iran; [email protected] 3 Department for Management of Science and Technology Development, Ton Duc Thang University, Ho Chi Minh City, Vietnam 4 Faculty of Information Technology, Ton Duc Thang University, Ho Chi Minh City, Vietnam 5 Department of Civil and Environmental Engineering, Hong Kong Polytechnic University, Hong Kong, China; [email protected] * Correspondence: [email protected] or [email protected] (M.T.S.); [email protected] (S.S.) Received: 1 April 2020; Accepted: 21 May 2020; Published: 24 May 2020 Abstract: Due to the stochastic nature and complexity of flow, as well as the existence of hydrological uncertainties, predicting streamflow in dam reservoirs, especially in semi-arid and arid areas, is essential for the optimal and timely use of surface water resources. In this research, daily streamflow to the Ermenek hydroelectric dam reservoir located in Turkey is simulated using deep recurrent neural network (RNN) architectures, including bidirectional long short-term memory (Bi-LSTM), gated recurrent unit (GRU), long short-term memory (LSTM), and simple recurrent neural networks (simple RNN). For this purpose, daily observational flow data are used during the period 2012–2018, and all models are coded in Python software programming language. -

Training Deep Networks Without Learning Rates Through Coin Betting
Training Deep Networks without Learning Rates Through Coin Betting Francesco Orabona∗ Tatiana Tommasi∗ Department of Computer Science Department of Computer, Control, and Stony Brook University Management Engineering Stony Brook, NY Sapienza, Rome University, Italy [email protected] [email protected] Abstract Deep learning methods achieve state-of-the-art performance in many application scenarios. Yet, these methods require a significant amount of hyperparameters tuning in order to achieve the best results. In particular, tuning the learning rates in the stochastic optimization process is still one of the main bottlenecks. In this paper, we propose a new stochastic gradient descent procedure for deep networks that does not require any learning rate setting. Contrary to previous methods, we do not adapt the learning rates nor we make use of the assumed curvature of the objective function. Instead, we reduce the optimization process to a game of betting on a coin and propose a learning-rate-free optimal algorithm for this scenario. Theoretical convergence is proven for convex and quasi-convex functions and empirical evidence shows the advantage of our algorithm over popular stochastic gradient algorithms. 1 Introduction In the last years deep learning has demonstrated a great success in a large number of fields and has attracted the attention of various research communities with the consequent development of multiple coding frameworks (e.g., Caffe [Jia et al., 2014], TensorFlow [Abadi et al., 2015]), the diffusion of blogs, online tutorials, books, and dedicated courses. Besides reaching out scientists with different backgrounds, the need of all these supportive tools originates also from the nature of deep learning: it is a methodology that involves many structural details as well as several hyperparameters whose importance has been growing with the recent trend of designing deeper and multi-branches networks. -

The Perceptron
The Perceptron Volker Tresp Summer 2019 1 Elements in Learning Tasks • Collection, cleaning and preprocessing of training data • Definition of a class of learning models. Often defined by the free model parameters in a learning model with a fixed structure (e.g., a Perceptron) (model structure learning: search about model structure) • Selection of a cost function which is a function of the data and the free parameters (e.g., a score related to the number of misclassifications in the training data as a function of the model parameters); a good model has a low cost • Optimizing the cost function via a learning rule to find the best model in the class of learning models under consideration. Typically this means the learning of the optimal parameters in a model with a fixed structure 2 Prototypical Learning Task • Classification of printed or handwritten digits • Application: automatic reading of postal codes • More general: OCR (optical character recognition) 3 Transformation of the Raw Data (2-D) into Pattern Vectors (1-D), which are then the Rows in a Learning Matrix 4 Binary Classification for Digit \5" 5 Data Matrix for Supervised Learning 6 M number of inputs (input attributes) Mp number of free parameters N number of training patterns T xi = (xi;0; : : : ; xi;M ) input vector for the i-th pattern xi;j j-th component of xi T X = (x1;:::; xN ) (design matrix) yi target for the i-th pattern T y = (y1; : : : ; yN ) vector of targets y^i model prediction for xi T di = (xi;0; : : : ; xi;M ; yi) i-th pattern D = fd1;:::; dN g (training data) T x = (x0; x1; : : : ; xM ) , generic (test) input y target for x y^ model estimate fw(x) a model function with parameters w f(x) the\true"but unknown function that generated the data Fine Details on the Notation • x is a generic input and xj is its j-th component. -
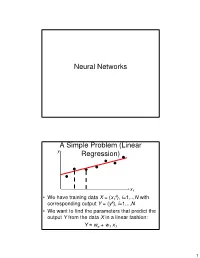
Neural Networks a Simple Problem (Linear Regression)
Neural Networks A Simple Problem (Linear y Regression) x1 k • We have training data X = { x1 }, i=1,.., N with corresponding output Y = { yk}, i=1,.., N • We want to find the parameters that predict the output Y from the data X in a linear fashion: Y ≈ wo + w1 x1 1 A Simple Problem (Linear y Notations:Regression) Superscript: Index of the data point in the training data set; k = kth training data point Subscript: Coordinate of the data point; k x1 = coordinate 1 of data point k. x1 k • We have training data X = { x1 }, k=1,.., N with corresponding output Y = { yk}, k=1,.., N • We want to find the parameters that predict the output Y from the data X in a linear fashion: k k y ≈ wo + w1 x1 A Simple Problem (Linear y Regression) x1 • It is convenient to define an additional “fake” attribute for the input data: xo = 1 • We want to find the parameters that predict the output Y from the data X in a linear fashion: k k k y ≈ woxo + w1 x1 2 More convenient notations y x • Vector of attributes for each training data point:1 k k k x = [ xo ,.., xM ] • We seek a vector of parameters: w = [ wo,.., wM] • Such that we have a linear relation between prediction Y and attributes X: M k k k k k k y ≈ wo xo + w1x1 +L+ wM xM = ∑wi xi = w ⋅ x i =0 More convenient notations y By definition: The dot product between vectors w and xk is: M k k w ⋅ x = ∑wi xi i =0 x • Vector of attributes for each training data point:1 i i i x = [ xo ,.., xM ] • We seek a vector of parameters: w = [ wo,.., wM] • Such that we have a linear relation between prediction Y and attributes X: M k k k k k k y ≈ wo xo + w1x1 +L+ wM xM = ∑wi xi = w ⋅ x i =0 3 Neural Network: Linear Perceptron xo w o Output prediction M wi w x = w ⋅ x x ∑ i i i i =0 w M Input attribute values xM Neural Network: Linear Perceptron Note: This input unit corresponds to the “fake” attribute xo = 1. -

Learning-Rate Annealing Methods for Deep Neural Networks
electronics Article Learning-Rate Annealing Methods for Deep Neural Networks Kensuke Nakamura 1 , Bilel Derbel 2, Kyoung-Jae Won 3 and Byung-Woo Hong 1,* 1 Computer Science Department, Chung-Ang University, Seoul 06974, Korea; [email protected] 2 Computer Science Department, University of Lille, 59655 Lille, France; [email protected] 3 Biotech Research and Innovation Centre (BRIC), University of Copenhagen, Nørregade 10, 1165 Copenhagen, Denmark; [email protected] * Correspondence: [email protected] Abstract: Deep neural networks (DNNs) have achieved great success in the last decades. DNN is optimized using the stochastic gradient descent (SGD) with learning rate annealing that overtakes the adaptive methods in many tasks. However, there is no common choice regarding the scheduled- annealing for SGD. This paper aims to present empirical analysis of learning rate annealing based on the experimental results using the major data-sets on the image classification that is one of the key applications of the DNNs. Our experiment involves recent deep neural network models in combination with a variety of learning rate annealing methods. We also propose an annealing combining the sigmoid function with warmup that is shown to overtake both the adaptive methods and the other existing schedules in accuracy in most cases with DNNs. Keywords: learning rate annealing; stochastic gradient descent; image classification 1. Introduction Citation: Nakamura, K.; Derbel, B.; Deep learning is a machine learning paradigm based on deep neural networks (DNNs) Won, K.-J.; Hong, B.-W. Learning-Rate that have achieved great success in various fields including segmentation, recognition, Annealing Methods for Deep Neural and many others. -
![Arxiv:1912.08795V2 [Cs.LG] 16 Jun 2020 the Teacher and Student Network Logits](https://docslib.b-cdn.net/cover/1686/arxiv-1912-08795v2-cs-lg-16-jun-2020-the-teacher-and-student-network-logits-2031686.webp)
Arxiv:1912.08795V2 [Cs.LG] 16 Jun 2020 the Teacher and Student Network Logits
Dreaming to Distill: Data-free Knowledge Transfer via DeepInversion Hongxu Yin1;2:∗ , Pavlo Molchanov1˚, Zhizhong Li1;3:, Jose M. Alvarez1, Arun Mallya1, Derek Hoiem3, Niraj K. Jha2, and Jan Kautz1 1NVIDIA, 2Princeton University, 3University of Illinois at Urbana-Champaign fhongxuy, [email protected], fzli115, [email protected], fpmolchanov, josea, amallya, [email protected] Knowledge Distillation DeepInversion Target class Synthesized Images Feature distribution regularization Teacher Cross Input (updated) logits entropy ... Feature Back Conv ReLU Loss Pretrained model (fixed) maps propagation BatchNorm ⟶ Noise Image Kullback–Leibler Pretrained model (fixed), e.g. ResNet50 1-JS divergence Teacher logits Student model Student Jensen- Inverted from a pretrained ImageNet ResNet-50 classifier (updated) Back Student model (fixed) logits Shannon (JS) (more examples in Fig. 5 and Fig. 6) propagation Loss divergence Adaptive DeepInversion Figure 1: We introduce DeepInversion, a method that optimizes random noise into high-fidelity class-conditional images given just a pretrained CNN (teacher), in Sec. 3.2. Further, we introduce Adaptive DeepInversion (Sec. 3.3), which utilizes both the teacher and application-dependent student network to improve image diversity. Using the synthesized images, we enable data-free pruning (Sec. 4.3), introduce and address data-free knowledge transfer (Sec. 4.4), and improve upon data-free continual learning (Sec. 4.5). Abstract 1. Introduction We introduce DeepInversion, a new method for synthesiz- ing images from the image distribution used to train a deep The ability to transfer learned knowledge from a trained neural network. We “invert” a trained network (teacher) to neural network to a new one with properties desirable for the synthesize class-conditional input images starting from ran- task at hand has many appealing applications. -

Towards Explaining the Regularization Effect of Initial Large Learning Rate in Training Neural Networks
Towards Explaining the Regularization Effect of Initial Large Learning Rate in Training Neural Networks Yuanzhi Li Colin Wei Machine Learning Department Computer Science Department Carnegie Mellon University Stanford University [email protected] [email protected] Tengyu Ma Computer Science Department Stanford University [email protected] Abstract Stochastic gradient descent with a large initial learning rate is widely used for training modern neural net architectures. Although a small initial learning rate allows for faster training and better test performance initially, the large learning rate achieves better generalization soon after the learning rate is annealed. Towards explaining this phenomenon, we devise a setting in which we can prove that a two layer network trained with large initial learning rate and annealing provably generalizes better than the same network trained with a small learning rate from the start. The key insight in our analysis is that the order of learning different types of patterns is crucial: because the small learning rate model first memorizes easy-to-generalize, hard-to-fit patterns, it generalizes worse on hard-to-generalize, easier-to-fit patterns than its large learning rate counterpart. This concept translates to a larger-scale setting: we demonstrate that one can add a small patch to CIFAR- 10 images that is immediately memorizable by a model with small initial learning rate, but ignored by the model with large learning rate until after annealing. Our experiments show that this causes the small learning rate model’s accuracy on unmodified images to suffer, as it relies too much on the patch early on. 1 Introduction It is a commonly accepted fact that a large initial learning rate is required to successfully train a deep network even though it slows down optimization of the train loss. -

How Does Learning Rate Decay Help Modern Neural Networks?
Under review as a conference paper at ICLR 2020 HOW DOES LEARNING RATE DECAY HELP MODERN NEURAL NETWORKS? Anonymous authors Paper under double-blind review ABSTRACT Learning rate decay (lrDecay) is a de facto technique for training modern neural networks. It starts with a large learning rate and then decays it multiple times. It is empirically observed to help both optimization and generalization. Common beliefs in how lrDecay works come from the optimization analysis of (Stochas- tic) Gradient Descent: 1) an initially large learning rate accelerates training or helps the network escape spurious local minima; 2) decaying the learning rate helps the network converge to a local minimum and avoid oscillation. Despite the popularity of these common beliefs, experiments suggest that they are insufficient in explaining the general effectiveness of lrDecay in training modern neural net- works that are deep, wide, and nonconvex. We provide another novel explanation: an initially large learning rate suppresses the network from memorizing noisy data while decaying the learning rate improves the learning of complex patterns. The proposed explanation is validated on a carefully-constructed dataset with tractable pattern complexity. And its implication, that additional patterns learned in later stages of lrDecay are more complex and thus less transferable, is justified in real- world datasets. We believe that this alternative explanation will shed light into the design of better training strategies for modern neural networks. 1 INTRODUCTION Modern neural networks are deep, wide, and nonconvex. They are powerful tools for representation learning and serve as core components of deep learning systems. They are top-performing models in language translation (Sutskever et al., 2014), visual recognition (He et al., 2016), and decision making (Silver et al., 2018). -

Natural Language Grammatical Inference with Recurrent Neural Networks
Accepted for publication, IEEE Transactions on Knowledge and Data Engineering. Natural Language Grammatical Inference with Recurrent Neural Networks Steve Lawrence, C. Lee Giles, Sandiway Fong ¡£¢£¤¦¥¨§ ©¦ ¦© £¢£©¦¤ ¥¤£ §©!¦©"¤ § $#&%' ()%* ©! +%, ¨-$. NEC Research Institute 4 Independence Way Princeton, NJ 08540 Abstract This paper examines the inductive inference of a complex grammar with neural networks – specif- ically, the task considered is that of training a network to classify natural language sentences as gram- matical or ungrammatical, thereby exhibiting the same kind of discriminatory power provided by the Principles and Parameters linguistic framework, or Government-and-Binding theory. Neural networks are trained, without the division into learned vs. innate components assumed by Chomsky, in an attempt to produce the same judgments as native speakers on sharply grammatical/ungrammatical data. How a recurrent neural network could possess linguistic capability, and the properties of various common recur- rent neural network architectures are discussed. The problem exhibits training behavior which is often not present with smaller grammars, and training was initially difficult. However, after implementing sev- eral techniques aimed at improving the convergence of the gradient descent backpropagation-through- time training algorithm, significant learning was possible. It was found that certain architectures are better able to learn an appropriate grammar. The operation of the networks and their training is ana- lyzed. Finally, the extraction of rules in the form of deterministic finite state automata is investigated. Keywords: recurrent neural networks, natural language processing, grammatical inference, government-and-binding theory, gradient descent, simulated annealing, principles-and- parameters framework, automata extraction. / Also with the Institute for Advanced Computer Studies, University of Maryland, College Park, MD 20742. -

Perceptron.Pdf
CS 472 - Perceptron 1 Basic Neuron CS 472 - Perceptron 2 Expanded Neuron CS 472 - Perceptron 3 Perceptron Learning Algorithm l First neural network learning model in the 1960’s l Simple and limited (single layer model) l Basic concepts are similar for multi-layer models so this is a good learning tool l Still used in some current applications (large business problems, where intelligibility is needed, etc.) CS 472 - Perceptron 4 Perceptron Node – Threshold Logic Unit x1 w1 x2 w2 �θ z xn wn € n 1 if x w ∑ i i ≥ θ z i=1 = n 0 if x w ∑ i i < θ i=1 CS 472 - Perceptron 5 Perceptron Node – Threshold Logic Unit x1 w1 x2 w2 � z xn wn n 1 if x w • Learn weights such that an objective ∑ i i ≥ θ function is maximized. z i=1 = n • What objective function should we use? 0 if x w ∑ i i < θ • What learning algorithm should we use? i=1 CS 472 - Perceptron 6 Perceptron Learning Algorithm x1 .4 .1 z x2 -.2 x x t n 1 2 1 if x w ∑ i i ≥ θ .8 .3 1 z i=1 = n .4 .1 0 0 if x w ∑ i i < θ i=1 CS 472 - Perceptron 7 First Training Instance .8 .4 .1 z =1 .3 -.2 net = .8*.4 + .3*-.2 = .26 x x t n 1 2 1 if x w ∑ i i ≥ θ .8 .3 1 z i=1 = n .4 .1 0 0 if x w ∑ i i < θ i=1 CS 472 - Perceptron 8 Second Training Instance .4 .4 .1 z =1 .1 -.2 net = .4*.4 + .1*-.2 = .14 x x t n 1 2 1 if x w ∑ i i ≥ θ i=1 .8 .3 1 z Dwi = (t - z) * c * xi = n .4 .1 0 0 if x w ∑ i i < θ i=1 CS 472 - Perceptron 9 Perceptron Rule Learning Dwi = c(t – z) xi l Where wi is the weight from input i to perceptron node, c is the learning rate, t is the target for the current instance, z is the current output,