An Investigation of Rubens Flame Tube Resonances
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Date Ideas Grillp
DATING & RELATIONSHIPS MEET THE CUTE GIRL P. 9 BFF GOT A BF? P. 29 Summer CHILL & DATE IDEAS GRILLP. 39 Mobile 8:01 PM 100% jobmatch Boostability, 6 487 3 Swipe right on Find out if Boostability is the right career match for you. It’s a Match! It’s a Match! It’s a Match! Lisse and Boostability have liked each other. Judy and Boostability have liked each other. Drew and Boostability have liked each other. Shared Interests (3) Shared Interests (3) Shared Interests (3) Flexible SEO & Great Growth Health, Vision, Work/Life BYU & Relaxed Work In-depth Schedule Ping Pong Co-workers Opportunity Dental, 401k Balance Foosball Environment Training "I was just looking for a job to pay the "When I started working here almost a "Boostability is awesome! I just came back bills when I rst applied at Boostability. I year ago, I was so impressed with the from bowling with our account management was immediately trained and was amazed culture. Part of my job description team and some of the executives. at how well I was treated, how easy-going included making sure I ordered a treat Recently, I attended an SLC/SEM everyone was, and how organized each month for all the employees. Are conference paid for by the company. everything was. I have progressed a lot, you kidding me? That's so great! I love Boostability fosters an environment of I really enjoy my job and look forward to working for a company that truly values growth, hard work and fun." coming to work each morning!" its employees." Drew, Lindon Ofce Lisse, Lehi Ofce Judy, Lehi Ofce boostability.com/ItsaMatch Couple your life-saving experience with a friend. -

BRIGHAM YOUNG UNIVERSITY GEOLOGY STUDIES Volume 44,1999
BRIGHAM YOUNG UNIVERSITY BRIGHAM YOUNG UNIVERSITY GEOLOGY STUDIES Volume 44,1999 CONTENTS Symmetrodonts from the Late Cretaceous of Southern Utah, and Comments on the Distribution of Archaic Mammalian Lineages Persisting into the Cretaceous of North America ................................ Richard L. Cifelli and Cynthia L. Gordon I A Large Protospongia Hicksi Hinde, 1887, from the Middle Cambrian Spence Shale of Southeastern Idaho ................................ Stephen B. Church, J. Keith Rigby, Lloyd E Gunther, and Val G. Gunther 17 Iapetonudus (N. gen.) and Iapetognathus Landing, Unusual Earliest Ordovician Multielement Conodont Taxa and Their Utility for Biostratigraphy .................................. Robert S. Nicoll, James E Miller, Godfrey S. Nowlan, John E. Repetski, and Raymond L. Ethington 27 Sponges from the Ibexian (Ordovician) McKelligon Canyon and Victorio Hills Formations in the Southern Franklin Mountains, Texas ...............J. Keith Rigby, C. Blair Linford, and David Y LeMone 103 Lower Ordovician Sponges from the Manitou Formation in Central Colorado ...................................................... J. Keith Rigby and Paul M. Myrow 135 Sponges from the Middle Permian Quinn River Formation, Bilk Creek Mountains, Humboldt County, Nevada .............................. J. Keith Rigby and Rex A. Hanger 155 A Publication of the Department of Geology Brigham Young University Provo, Utah 84602 Editor Bart J. Kowallis Brigham Young University Geology Studies is published by the Department of Geology. This publication consists of graduate student and faculty research within the department as well as papers submitted by outside contributors. Each article submitted is externally reviewed by at least two qualified persons. ISSN 0068-1016 6-99 650 29580 Sponges from the Middle Permian Quinn River Formation, Bilk Creek Mountains, Humboldt County, Nevada J. KEITH RIGBY Department of Geology, S-389 Eyring Science Center, Brigham Young University, Provo, Utah 84602-4606 REX A. -
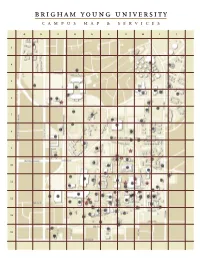
PDF BYU Campus
brigham young university campus map & services A B C D E F G H I J 3 4 5 6 7 8 9 10 11 12 13 14 campus facilities 1 ALLN Allen Hall (Museum of Peoples and Cultures) C/14 49 SWKT Kimball Tower, Spencer W. F/12 2 ALUM Alumni House E/9 50 AKH Knight Hall, Amanda B,C/14 3 FARM Animal Science Farm C/1,2 51 JKHB Knight Humanities Building, Jesse F/10 4 AXMB Auxiliary Maintenance Building I/5,6 52 KMB Knight Mangum Building G,H/12,13 5 B-21 to B-32 (Service Buildings) G/12 53 AXLB Laundry Building, Auxiliary Services I/6 6 B-34, B-38, B-41, B-51 (Misc. Temporary Buildings) G/12 54 HBLL Lee Library, Harold B. F,G/10,11 7 B66 B-66 Classroom/Lab Building I/12 55 MSRB Maeser Building, Karl G. E/13 8 B67 B-67 Service Building C/2 56 MC Marriott Center, J. Willard F,G/7,8 9 B72 B-72 Building (LDS Foundation) C/8 57 MARB Martin Building, Thomas L. F,G/12 10 B77 B-77 Service Building (Former UVSC Building) C/8,9 58 MB McDonald Building, Howard S. G/13 11 MLBM Bean Life Science Museum, Monte L. G/8 59 MCKB McKay Building, David O. E/12 12 B-49 Benson Agriculture and Food Institute, Ezra Taft F/14 60 MLRP Miller Park (Baseball/Softball Complex) E,F/7 13 BNSN Benson Building, Ezra Taft F/12,13 61 MTC Missionary Training Center H,I/4,5 14 WSC Bookstore, BYU G/11 62 PPMV Motor Pool Vehicle Shelter I/12,13 15 BRWB Brewster Building, Sam F. -

Time Reversal Acoustics Applied to Rooms of Various Reverberation Times
Time reversal acoustics applied to rooms of various reverberation times Michael H. Denison and Brian E. Andersona) Acoustics Research Group, Department of Physics and Astronomy, Brigham Young University, N283 Eyring Science Center, Provo, Utah 84602, USA (Received 21 July 2018; revised 6 November 2018; accepted 8 November 2018; published online 3 December 2018) Time Reversal (TR) is a technique that may be used to focus an acoustic signal at a particular point in space. While many variables contribute to the quality of TR focusing of sound in a particular room, the most important have been shown to be the number of sound sources, signal bandwidth, and absorption properties of the medium as noted by Ribay, de Rosny, and Fink [J. Acoust. Soc. Am. 117(5), 2866–2872 (2005)]. However, the effect of room size on TR focusing has not been explored. Using the image source method algorithm proposed by Allen and Berkley [J. Acoust. Soc. Am. 65(4), 943–950 (1979)], TR focusing was simulated in a variety of rooms with different absorption and volume properties. Experiments are also conducted in a couple rooms to verify the simulations. The peak focal amplitude, the temporal focus quality, and the spatial focus clarity are defined and calculated for each simulation. The results are used to determine the effects of absorp- tion and room volume on TR. Less absorption increases the amplitude of the focusing and spatial clarity while decreasing temporal quality. Dissimilarly, larger volumes decrease focal amplitude and spatial clarity while increasing temporal quality. VC 2018 Acoustical Society of America. https://doi.org/10.1121/1.5080560 [EF-G] Pages: 3055–3066 I. -

National Academy of Sciences July 1, 1973
NATIONAL ACADEMY OF SCIENCES JULY 1, 1973 OFFICERS Term expires President-PHILIP HANDLER June 30, 1975 Vice-President-SAUNDERS MAC LANE June 30, 1977 Home Secretary-ALLEN V. ASTIN June 30, 1975 Foreign Secretary-HARRISON BROWN June 30, 1974 Treasurer- E. R. PIORE June 30, 1976 Executive Officer Comptroller John S. Coleman Aaron Rosenthal Buiness Manager Bernard L. Kropp COUNCIL *Astin, Allen V. (1975) Marshak, Robert E. (1974) Babcock, Horace W. (1976) McCarty, Maclyn (1976) Bloch, Konrad E. (1974) Pierce, John R. (1974) Branscomb, Lewis M. (1975) *Piore, E. R. (1976) *Brown, Harrison (1974) Pitzer, Kenneth S. (1976) *Cloud, Preston (1975) *Shull, Harrison (1974) Eagle, Harry (1975) Westheimer, Frank H. (1975) *Handler, Philip (1975) Williams, Carroll M. (1976) *Mac Lane, Saunders (1977) * Members of the Executive Committee of the Council of the Academy. SECTIONS The Academy is divided into the following Sections, to which members are assigned at their own choice: (1) Mathematics (10) Microbiology (2) Astronomy (11) Anthropology (3) Physics (12) Psychology (4) Engineering (13) Geophysics (5) Chemistry (14) Biochemistry (6) Geology (15) Applied Biology (7) Botany (16) Applied Physical and Mathematical Sciences (8) Zoology (17) Medical Sciences (9) Physiology (18) Genetics (19) Social, Economic, and Political Sciences In the alphabetical list of members, the number in parentheses, following year of election, indicates the Section to WCiph the member belongs. 3009 Downloaded by guest on September 25, 2021 3010 Members N.A.S. Organization CLASSES Ames, Bruce Nathan, 1972 (14), Department of Biochem- istry, University of California, Berkeley, California The members of Sections are grouped in the following Classes: 94720 Anderson, Carl David, 1938 (3), California Institute of I. -

Program Guide
Cascade E Level 3 11:30 AM - 12:30 PM Monday, 7/22/19 when was the last time you really thought about how your students are graded? 1980-something 1999 2019 instructors once graded Early online grading is Automatically graded FBD for process and provided convenient, but lacks drawings & symbolic expressions , hand-written feedback . problem-solving function. plus student-provided feedback . Reinforcing Physics Video Advanced the Problem-Solving Series for the Academic Integrity Process Flipped Classroom Tool Suite BOOTH 100 TheExpertTA.com SUMMER MEETING 2019 July 20-24 Provo, Utah Provo, UT Meeting Information ............................. 4 Committee Meetings............................. 5 July 20–24, 2019 AAPT Awards ......................................... 6 Plenaries ............................................... 9 Utah Valley Convention Center Commercial Workshops ......................... 11 and Provo Marriott Hotel and Conference Bus Schedule for Workshops ................. 13 Exhibitor Information ............................ 14 Center SPS Posters ............................................ 23 Workshop Abstracts .............................. 25 Session Abstracts .................................. 36 Monday .............................................. 36 Tuesday ............................................. 92 Wednesday ......................................... 130 Participants’ Index ................................. 168 Maps ..................................................... 174 American Association of Physics Teachers -

Utah Space Grant Consortium Lead Institution: University of Utah Director: Dr
FY 2018 Year 4 Extension Annual Performance Document Utah Space Grant Consortium Lead Institution: University of Utah Director: Dr. Joseph Orr Telephone Number: (8081) 573-2091 Consortium URL: http://www.utahspacegrant.com Grant Number: NNX15AI24H Lines of Business (LOBs): NASA Internships, Fellowships, and Scholarships; STEM Engagement; Institutional Engagement; Educator Professional Development A. PROGRAM DESCRIPTION: The National Space Grant College and Fellowship Program consists of 52 state-based, university-led Space Grant Consortia in each of the 50 states plus the District of Columbia and the Commonwealth of Puerto Rico. Annually, each consortium receives funds to develop and implement student fellowships and scholarships programs; interdisciplinary space- related research infrastructure, education, and public service programs; and cooperative initiatives with industry, research laboratories, and state, local, and other governments. Space Grant operates at the intersection of NASA’s interest as implemented by alignment with the Mission Directorates and the state’s interests. Although it is primarily a higher education program, Space Grant programs encompass the entire length of the education pipeline, including elementary/secondary and informal education. The Utah Space Grant Consortium is a Designated Consortium funded at a level of $760,000 for fiscal year 2018. B. PROGRAM GOALS: Goal 1: In alignment with the NASA Internships, Fellowships, and Scholarships (NIFS) Line of Business, advertise and award Space Grant fellowships, scholarships, and internship awards to students enrolled in Utah institutions of higher education, thereby contributing to our Nation’s future workforce and fuel an increased interest in STEM disciplines. SMART Objective 1: In 2018-19 we plan to award 20 fellowships at the graduate student level. -

Introduction to the Development of a Radio Astronomy System at Brigham Young University
Brigham Young University BYU ScholarsArchive Theses and Dissertations 2014-07-01 Introduction to the Development of a Radio Astronomy System at Brigham Young University Daniel Robert Blakley Brigham Young University - Provo Follow this and additional works at: https://scholarsarchive.byu.edu/etd Part of the Astrophysics and Astronomy Commons BYU ScholarsArchive Citation Blakley, Daniel Robert, "Introduction to the Development of a Radio Astronomy System at Brigham Young University" (2014). Theses and Dissertations. 5297. https://scholarsarchive.byu.edu/etd/5297 This Thesis is brought to you for free and open access by BYU ScholarsArchive. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of BYU ScholarsArchive. For more information, please contact [email protected], [email protected]. Introduction to the Development of a Radio Astronomy System at Brigham Young University Daniel Robert Blakley A thesis submitted to the faculty of Brigham Young University in partial fulfillment of the requirements for the degree of Master of Science Victor Migenes, Chair J. Ward Moody Karl Warnick Department of Physics and Astronomy Brigham Young University July 2014 Copyright © 2014 Daniel Robert Blakley All Rights Reserved ABSTRACT Introduction to the Development of a Radio Astronomy System at Brigham Young University Daniel Robert Blakley Department of Physics and Astronomy, BYU Master of Science The intent of this project was founded upon the need to train students in the techniques of radio astronomy with the purpose of establishing a radio telescope in order to teach the principles and practice of radio astronomy. This document describes the theory and research necessary to establish the 1st generation radio telescope system within the Department of Physics and Astronomy at Brigham Young University. -

Supplement to the 2011 AP Stylebook Revised August 18, 2011 See Page 15 for Church Style Items
Supplement to the 2011 AP Stylebook Revised August 18, 2011 See page 15 for Church style items. See page 18 for sports style items. As a courtesy to others, please leave in the newsroom. Supplement to the 2011 AP Stylebook Revised August 18, 2011 See page 15 for Church style items. See page 18 for sports style items. teaching careers as assistant professors, then progress to associate professors, A then full professors. Adjunct faculty are usually employed elsewhere but teach at academic degrees Use bachelor’s the university. Professors emeritus are degree, master’s degree, doctorate. officially retired but may still teach a class Doctoral is the adjective form of or perform other duties at the university. doctorate. When necessary, you may Where appropriate, you may use Dean, use B.A., B.S., M.A., M.S., MBA, Ph.D. Department Chair, President, Provost or and other degree abbreviations after Vice President in front of a name on first the name. Follow AP style: “if mention reference. In the case of the president of degrees is necessary to establish of the university, the title must be used someone’s credentials, the preferred on every subsequent reference. These form is to avoid an abbreviation and use titles are never abbreviated. instead a phrase such as: John Jones, who has a doctorate in psychology. Don’t use addresses should be listed by house Dr. before the name unless the person number in numerals, followed by holds a medical degree. direction abbreviated, and street: 1084 S. 1000 West. Don’t abbreviate the street academic titles You may use the number — no 10th West. -

Brigham Young University
Coordinates: 40°15′3″N 111°38′57″W Brigham Young University Brigham Young University (BYU) is a private research university sponsored by The Church of Jesus Christ of Latter-day Saints (LDS Church) and located in Provo, Brigham Young Utah. The university is accredited by the Northwest Commission on Colleges and Universities.[9] Run under the auspices of the church's parent organization, the University Church Educational System (CES), BYU is classified among "R2: Doctoral Universities – High Research Activity" with "more selective, lower transfer-in" admissions.[10] The university's primary emphasis is on undergraduate education in 179 majors, but it also has 62 master's and 26 doctoral degree programs.[11] The university also administers two satellite campuses, one in Jerusalem and one in Salt Lake City. Students attending BYU agree to follow an honor code that mandates behavior in Former names Brigham line with LDS teachings, such as academic honesty, adherence to dress and grooming standards, abstinence from extramarital sex and homosexual behavior, and no Young consumption of illegal drugs, coffee, tea, alcohol, or tobacco.[12] Approximately 99 Academy [13] percent of the students are members of the LDS Church. The university (1875–1903) curriculum includes religious education, with required courses in the Bible (King James Version), LDS scripture, doctrine, and history,[14] and the university sponsors Motto No official weekly devotional assemblies with most speakers addressing religious topics.[15] motto[1] Sixty-six percent of students either delay enrollment or take a hiatus from their studies to serve as LDS missionaries.[16][17] An education at BYU is less expensive Unofficial than at similar private universities,[18] since "a significant portion" of the cost of mottoes operating the university is subsidized by the church's tithing funds.[19] include: BYU's athletic teams compete in Division I of the NCAA and are collectively known The glory of as the Cougars. -

Meeting Program (PDF)
Cascade E Level 3 11:30 AM - 12:30 PM Monday, 7/22/19 when was the last time you really thought about how your students are graded? 1980-something 1999 2019 instructors once graded Early online grading is Automatically graded FBD for process and provided convenient, but lacks drawings & symbolic expressions , hand-written feedback . problem-solving function. plus student-provided feedback . Reinforcing Physics Video Advanced the Problem-Solving Series for the Academic Integrity Process Flipped Classroom Tool Suite BOOTH 100 TheExpertTA.com SUMMER MEETING 2019 July 20-24 Provo, Utah Provo, UT Meeting Information ............................. 4 Committee Meetings............................. 5 July 20–24, 2019 AAPT Awards ......................................... 6 Plenaries ............................................... 9 Utah Valley Convention Center Commercial Workshops ......................... 11 and Provo Marriott Hotel and Conference Bus Schedule for Workshops ................. 13 Exhibitor Information ............................ 14 Center SPS Posters ............................................ 23 Workshop Abstracts .............................. 25 Session Abstracts .................................. 36 Monday .............................................. 36 Tuesday ............................................. 92 Wednesday ......................................... 130 Participants’ Index ................................. 168 Maps ..................................................... 174 American Association of Physics Teachers -

A History of the Student Newspaper and Its Early Predecessors at Brigham Young University from 1878 to 1965
Brigham Young University BYU ScholarsArchive Theses and Dissertations 1966 A History of the Student Newspaper and Its Early Predecessors at Brigham Young University From 1878 to 1965 Lawrence Hall Bray Brigham Young University - Provo Follow this and additional works at: https://scholarsarchive.byu.edu/etd Part of the Journalism Studies Commons, and the Mormon Studies Commons BYU ScholarsArchive Citation Bray, Lawrence Hall, "A History of the Student Newspaper and Its Early Predecessors at Brigham Young University From 1878 to 1965" (1966). Theses and Dissertations. 4552. https://scholarsarchive.byu.edu/etd/4552 This Thesis is brought to you for free and open access by BYU ScholarsArchive. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of BYU ScholarsArchive. For more information, please contact [email protected], [email protected]. A HISTORY OF THE STUDENT NEWSPAPER AND ITS EARLY PREDECESSORS AT BRIGHAM YOUNG UNIVERSITY FROM 1878 to 1965 A Thesis Presented to the Department of Communications Brigham Young University In Partial Fulfillment of the Requirements for the Degree Master of Arts by Lawrence Hall Bray May 1966 ACKNOWLEDGMENTS The writer is indebted to many people for the inspir ation and direction he has received in the pursuit of higher education, and in the writing of this thesis. A few educa tors and others will be mentioned personally although there are many worthy of mention who are not included. Mr. and Mrs. Vern B. Bray, the writer's parents were instrumental in implanting in him, at an early age, the value of education, and have never failed to build the writer's self-confidence and will to succeed.