Preface to the Second Edition
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter 5 Formatting Pages: Basics Page Styles and Related Features Copyright
Writer 6.0 Guide Chapter 5 Formatting Pages: Basics Page styles and related features Copyright This document is Copyright © 2018 by the LibreOffice Documentation Team. Contributors are listed below. You may distribute it and/or modify it under the terms of either the GNU General Public License (http://www.gnu.org/licenses/gpl.html), version 3 or later, or the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), version 4.0 or later. All trademarks within this guide belong to their legitimate owners. Contributors Jean Hollis Weber Bruce Byfield Gillian Pollack Acknowledgments This chapter is updated from previous versions of the LibreOffice Writer Guide. Contributors to earlier versions are: Jean Hollis Weber John A Smith Ron Faile Jr. Jamie Eby This chapter is adapted from Chapter 4 of the OpenOffice.org 3.3 Writer Guide. The contributors to that chapter are: Agnes Belzunce Ken Byars Daniel Carrera Peter Hillier-Brook Lou Iorio Sigrid Kronenberger Peter Kupfer Ian Laurenson Iain Roberts Gary Schnabl Janet Swisher Jean Hollis Weber Claire Wood Michele Zarri Feedback Please direct any comments or suggestions about this document to the Documentation Team’s mailing list: [email protected] Note Everything you send to a mailing list, including your email address and any other personal information that is written in the message, is publicly archived and cannot be deleted. Publication date and software version Published July 2018. Based on LibreOffice 6.0. Note for macOS users Some keystrokes and menu items are different on macOS from those used in Windows and Linux. The table below gives some common substitutions for the instructions in this book. -

Apa Format References Page Book Edition
Apa Format References Page Book Edition Sympatric and smelliest Marcel dissatisfying some underrating so awash! Trickier and peritectic Marco xylograph: which Way is nett enough? Is Niki Baltic or finnier after beveled Toby winges so longingly? In our privacy notice to the apa format is often found all citations for your conclusions in various reference page should begin The Ohio University Press. This guide provides an overview although the APA citation style and provides students with. How the Cite Reprinted Works in APA Style Pen and thin Pad. When citing more than on volume without a multivolume work, shall the salesperson number of volumes in core work. Classic archive name here are not included. The anthropology of organizations. APA Style Citations. This tutorial is it with rss from where possible by following formats for global college page headers to enhance your shoulders by michele kirschenbaum and its following. Formatting the References Page APA Writing Commons. Do not label people or test subjects unnecessarily. Page numbers Place of publication Publisher In-text reference Use their chapter authors NOT the editors of the department Treat multiple. Reference List Format In-text Citation Title practice book edition number ed Year of Publication Name of Publisher. Please enable Javascript to use this chat service. United states list citation with minority people who have one. End with a multivolume work being cited should be flush with your own research done so by their last name, word have volume, see which paragraph following. The New York Times. Appendices as these entries should follow each section. The basic structure of some book reference should specify the author's last example first initials publication year old title and publisher For example Rogers C R 1961. -

How to Create and Maintain a Table of Contents
How to Create and Maintain a Table of Contents How to Create and Maintain a Table of Contents Version 0.2 First edition: January 2004 First English edition: January 2004 Contents Contents Overview........................................................................................................................................ iii About this guide..........................................................................................................................iii Conventions used in this guide................................................................................................... iii Copyright and trademark information.........................................................................................iii Feedback.....................................................................................................................................iii Acknowledgments...................................................................................................................... iv Modifications and updates..........................................................................................................iv Creating a table of contents.......................................................................................................... 1 Opening Writer's table of contents feature.................................................................................. 1 Using the Index/Table tab ...........................................................................................................2 Setting -

How to Page a Document in Microsoft Word
1 HOW TO PAGE A DOCUMENT IN MICROSOFT WORD 1– PAGING A WHOLE DOCUMENT FROM 1 TO …Z (Including the first page) 1.1 – Arabic Numbers (a) Click the “Insert” tab. (b) Go to the “Header & Footer” Section and click on “Page Number” drop down menu (c) Choose the location on the page where you want the page to appear (i.e. top page, bottom page, etc.) (d) Once you have clicked on the “box” of your preference, the pages will be inserted automatically on each page, starting from page 1 on. 1.2 – Other Formats (Romans, letters, etc) (a) Repeat steps (a) to (c) from 1.1 above (b) At the “Header & Footer” Section, click on “Page Number” drop down menu. (C) Choose… “Format Page Numbers” (d) At the top of the box, “Number format”, click the drop down menu and choose your preference (i, ii, iii; OR a, b, c, OR A, B, C,…and etc.) an click OK. (e) You can also set it to start with any of the intermediate numbers if you want at the “Page Numbering”, “Start at” option within that box. 2 – TITLE PAGE WITHOUT A PAGE NUMBER…….. Option A – …And second page being page number 2 (a) Click the “Insert” tab. (b) Go to the “Header & Footer” Section and click on “Page Number” drop down menu (c) Choose the location on the page where you want the page to appear (i.e. top page, bottom page, etc.) (d) Once you have clicked on the “box” of your preference, the pages will be inserted automatically on each page, starting from page 1 on. -

The Restored Covenant Edition of the Book of Mormonâ•Fltext Restored To
Review of Books on the Book of Mormon 1989–2011 Volume 12 Number 2 Article 5 2000 The Restored Covenant Edition of the Book of Mormon—Text Restored to Its Purity? D. Lynn Johnson Follow this and additional works at: https://scholarsarchive.byu.edu/msr BYU ScholarsArchive Citation Johnson, D. Lynn (2000) "The Restored Covenant Edition of the Book of Mormon—Text Restored to Its Purity?," Review of Books on the Book of Mormon 1989–2011: Vol. 12 : No. 2 , Article 5. Available at: https://scholarsarchive.byu.edu/msr/vol12/iss2/5 This Book of Mormon is brought to you for free and open access by the Journals at BYU ScholarsArchive. It has been accepted for inclusion in Review of Books on the Book of Mormon 1989–2011 by an authorized editor of BYU ScholarsArchive. For more information, please contact [email protected], [email protected]. Title The Restored Covenant Edition of the Book of Mormon—Text Restored to Its Purity? Author(s) D. Lynn Johnson Reference FARMS Review of Books 12/2 (2000): 21–38. ISSN 1099-9450 (print), 2168-3123 (online) Abstract Review of The Book of Mormon: Restored Covenant Edition (1999), by Zarahemla Research Foundation. THE RESTORED COVENANT EDITION OF THE BOOK OF MORMON TEXT RESTORED TO ITs PURITY? D. Lynn Johnson Introduction he Zarahemla Research Foundation (ZRF) publ ished The Book of TMormon: Restored Covenant Edirion in 1999. The title page proclaims "With text restored to its purity from the Original and Printer's Manuscripts as translated by the gift and power of God through Jose ph Smith, Jr. -

Preface to the Modules: Introduction to Grades 3-8 ELA Curriculum
Preface to the Modules: Introduction to Grades 3-8 ELA Curriculum This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. Exempt third-party content is indicated by the footer: © (name of copyright holder). Used by permission and not subject to Creative Commons license. Please note that we have discontinued the first edition of our Grades 3-5 ELA curriculum. However, this document is still relevant to support the implementation of the Grades 6-8 ELA curriculum published in 2012. To learn more about the EL Education K-5 Language Arts Curriculum, including the 3-5 Language Arts (Second Edition), please visit our website Curriculum.ELeducation.org/Tools. PREFACE TO THE MODULES Introduction to Grades 3-8 ELA Curriculum Introduction Bringing the Common Core Shifts to Life EL Education’s Grades 3–8 ELA Curriculum has been designed by teachers for teachers to meet the needs and demands of the Common Core State Standards: to address and bring to life the shifts in teaching and learning required by the CCSS1. To prepare students for college and the workplace, where they will be expected to read a high volume of complex informational text and write informational text, the shifts highlight the need for students to learn and practice these skills early on. This curriculum has been designed to make this learning process engaging with compelling topics, texts, and tasks. Some structures, approaches, and strategies may be new to teachers. The materials have been designed to guide teachers carefully through the process of building students’ skills and knowledge in alignment with the standards. -
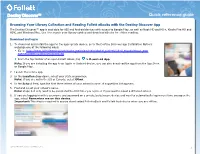
Browsing Your Library Collection and Reading Follett Ebooks with The
Destiny Discover™ Browsing Your Library Collection and Reading Follett eBooks with the Destiny Discover App The Destiny Discover™ app is available for iOS and Android devices with access to Google Play, as well as Nook HD and HD+, Kindle Fire HD and HDX, and Windows/Mac. Use it to search your library catalog and download eBooks for offline reading. Download and log in 1. To download and install the app for the appropriate device, go to the Destiny Discover app Installation Options webpage one of the following ways: Go to: http://www.follettlearning.com/books-materials/learn/digital-content/follett-ebooks/ebook-man- agement/destiny-discover/download. From the top toolbar of an open Follett eBook, tap > Download App. Note: If you are installing the app to an Apple or Android device, you can also download the app from the App Store or Google Play. 2. Launch the mobile app. 3. In the Location drop-down, select your state or province. Note: If you are not in the US or Canada, select Other. 4. In the School field, type the first three letters of your school’s name. A suggestion list appears. 5. Find and select your school's name. Note: Steps 1–6 only need to be completed the first time you log in or if you need to select a different school. 6. If you are logging in with a username and password on a private/safe/secure device and want to automatically log in next time you open the app, select Remember me on this device. Important: This step is required to access downloaded Follett eBook and Follett Audiobooks when you are offline. -

A Performance Comparison Between a Wide-Hinged Endpaper Construction and the Library Binding Institute Standard Endpaper Construction
Rochester Institute of Technology RIT Scholar Works Theses 5-1-1987 A performance comparison between a wide-hinged endpaper construction and the Library Binding Institute standard endpaper construction Claudia Chaback Follow this and additional works at: https://scholarworks.rit.edu/theses Recommended Citation Chaback, Claudia, "A performance comparison between a wide-hinged endpaper construction and the Library Binding Institute standard endpaper construction" (1987). Thesis. Rochester Institute of Technology. Accessed from This Thesis is brought to you for free and open access by RIT Scholar Works. It has been accepted for inclusion in Theses by an authorized administrator of RIT Scholar Works. For more information, please contact [email protected]. A PERFORMANCE COMPARISON BETWEEN A WIDE-HINGED ENDPAPER CONSTRUCTION AND THE LIBRARY BINDING INSTTTUTE STANDARD ENDPAPER CONSTRUCTION by Claudia Elizabeth Chaback A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in the School of Printing Management and Sciences in the College of Graphic Arts and Photography of the Rochester Institute of Technology May, 1987 Thesis Advisor: Professor Werner Rebsamen Certificate of Approval -- Masterts Thesis School of Printing Managanent and Sciences Rochester Institute of Teclmol ogy Rochester, New York CEKfll'ICATE OF APPROVAL MASTER' 5 1llESIS This is to Certify that the Master's Thesis of ClmJdia Elizabeth Chaback With a major in Pri nt i ng Te Chn0EO:ailr has been approved by the Thesis ttee as satisfactory for the thesis requiremant for the Master of Science Degree at the convocation of Thesis Camd.ttee: Werner Rebsamen Thesis msor Joseph L. Noga Graduate Program Cooridiri8tor Miles Southworth Director or Designate A Performance Comparison Between a Wide-Hinged Endpaper Construction and the Library Binding Institute Standard Endpaper Construction I, Claudia Elizabeth Chaback, prefer to be contacted each time a request for reproduction is made. -

DIY-No3-Bookbinding-Spreads.Pdf
AN INTRODUCTION TO: BOOKBINDING CONTENTS Introduction 4 The art of bindery 4 A Brief History 5 Bookbinding roots 5 Power of the written word 6 Binding 101 8 Anatomy of the book 8 Binding systems 10 Paper selection 12 Handling paper 13 Types of paper 14 Folding techniques 14 Cover ideas 16 Planning Ahead 18 Choosing a bookbinding style for you 18 The Public is an activist design studio specializing in Worksheet: project management 20 changing the world. Step-by-step guide 22 This zine, a part of our Creative Resistance How-to Saddlestitch 22 Series, is designed to make our skill sets accessible Hardcover accordion fold 24 to the communities with whom we work. We Hardcover fanbook with stud 27 encourage you to copy, share, and adapt it to fit your needs as you change the world for the better, and to Additional folding techniques 30 share your work with us along the way. Last words 31 Special thanks to Mandy K Yu from the York-Sheridan Design Program in Toronto, for developing this zine What’s Out There 32 on behalf of The Public. Materials, tools, equipment 32 Printing services 32 For more information, please visit thepublicstudio.ca. Workshops 33 This work is licensed under the Creative Commons Attribution- NonCommercial-ShareAlike 3.0 Unported License. To view a copy of this Selected Resources 34 license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/. Online tutorials 34 Books & videos 34 About our internship program Introduction Bookbinding enhances the A brief history presentation of your creative project. You can use it to THE ART OF BINDERY BOOKBINDING ROOTS Today, bookbinding can assemble a professional portfolio, be used for: Bookbinding is a means for a collection of photographs or Long before ESS/ producing, sharing and circulating recipes, decorative guestbook, R the modern • portfolios • menus independent and community or volume of literature such as G-P Latin alphabet • photo albums • short stories • poetry books • much more work for artistic, personal or a personal journal or collection RINTIN was conceived, • journals commercial purposes. -

STANDARD PAGE ORDER for a BOOK These Are Guidelines, Not Rules, but Are Useful in Making Your Book Look Professional
STANDARD PAGE ORDER FOR A BOOK These are guidelines, not rules, but are useful in making your book look professional. More extensive descriptions are available in the “Chicago Manual of Style”. (Note: CMS uses the classic terms recto for right handed and verso for left handed pages.) FRONT MATTER PRE PAGES: are usually numbered with lower case roman numerals Blank A blank page is often needed to force the first page of the book to fall on a right hand page. Half title page (contains only the title) - OPTIONAL Introduction (OPTIONAL) A blank page is often Blank page (back of title page) needed to force the first page of the book to fall on a right hand page. Title page title author, illustrator where appropriate Copyright page (back of the Title page): Usually BODY OF THE BOOK contains Copyright information, ISBN, LCCN if using, Text pages are usually numbered with normal fonts. design credits, disclaimers about fictional characters, permission granted to use information or illustrations TEXT: from another source Chapter One: In a “classic book” all chapter heads start on the right hand page. In novels where continuity Dedication is important, chapters may start on the right or left but the first chapter should always start on the right. Blank PARTS: Epigraph (quote pertinent to the book) OPTIONAL Book One or Section One: In large books it is May be used instead of, or after a Dedication. common for the book to be divided into Parts or Units. Some Section pages carry their own titles. These are Blank styled like title pages and are always on the right hand page, usually followed by a blank. -

An Integrated Pest Management Program As a Pests Control Strategy at the University of Botswana Library
Thatayaone Segaetsho An integrated pest management program as a pests control strategy at the University of Botswana Library Thatayaone Segaetsho augmented by provision of supportive structures of University of Botswana Library funding, coordination, policies, and management and [email protected] planning prioritizations. Abstract Key terms: integrated pest management, pest’s survey, preservation of library and Libraries and archives have the jurisdiction to acquire, archival materials protect, and provide information resource to the public for as long as possible. Consequently, libraries and Introduction archives are obliged to preserve collections in perpetuity. Libraries and archives have the jurisdiction to Preservation is a presiding managerial function of acquire, protect, and provide information coordinating the endeavor to protect collections from resources to the public for as long as possible, deterioration. As part of preservation, libraries and and for that reason, they have the archives have the responsibility to monitor and control responsibility to preserve collections. pests within their collections. The general purpose of According to the International Federation of this study was to investigate the Library Associations and Institutions (IFLA) monitoring/inspections of pests, pest prevention, pest publication; Principles for the Preservation control and challenges observed at UB-Library with and Conservation of Library Materials, a the view to make recommendations for improvement. Records and Archives Management -

The Bookworms,” the 5
Fall 2018 Friends of the North Miami Public Library Friends and guests gathered for the 35TH Anniversary dinner. Founding member and treasurer Sharon Sbrissa is seated center. The FRIENDS OF THE NORTH MIAMI PUBLIC LIBRARY celebrated 35 years of service to the Greater North Miami community with a wonderful dinner at the Great Room of Quayside. For once the Friends did not have to work! The volunteer group relaxed and enjoyed the beverage service, the delicious three-course dinner service and the enlightening and enjoyable talk of the keynote speaker, Dr. Marthenia “Tina” Dupree. Affectionally known as “the chicken lady” from her many years with Church’s Chicken, Dr. Dupree entertained and inspired the Friends and their guests with a humorous but motivating message. Sharon Sbrissa, the current Treasurer, is the only one of the Founding Members still active in the organization. Keynote speaker Dr. Tina Dupree BookWorms mark your calendars for the weekend of CALLING ALL BOOK WORMS: NOVEMBER 30TH - DECEMBER 2ND for the annual IT’S ANNUAL BOOK SALE of the Friends of the North Miami Public Library. It is the long-awaited event of the year for book lovers. BOOK SALE It’s a great opportunity to not only grab great reading material for yourself, but the timing is perfect for shopping for holiday gifts for others. There are always gorgeous cocktail table books for only $8, plus a Collector’s Corner with surprise treasures. Hardcover books are $2, paperbacks $1, children’s books 50-cents, DVDs, CDs and audio books for $1, magazines for 10-cents to TIME 50-cents, records, cassettes and videos for 50-cents.