DOCSLIB.ORG

Exogamic Or Endogamic

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Exogamic Or Endogamic ST. PETERSBURG UNIVERSITY THE INTERNATIONAL SOCIETY OF DYNAMIC GAMES (Russian Chapter) GAME THEORY AND MANAGEMENT The Seventh International Conference Game Theory and Management GTM2013 June 26-28, 2013, St. Petersburg, Russia ABSTRACTS Edited by Leon A. Petrosyan and Nikolay A. Zenkevich St. Petersburg University St. Petersburg 2013 УДК 518.9, 517.9, 681.3.07 GAME THEORY AND MANAGEMENT. Collected abstracts of papers presented on the Seventh International Conference Game Theory and Management / Editors Leon A. Petrosyan and Nikolay A. Zenkevich. – SPb.: Graduate School of Management SPbU, 2013. – 274 p. The collection contains abstracts of papers accepted for the Seventh International Conference Game Theory and Management (June 26–28, 2013, St. Petersburg University, St. Petersburg, Russia). The presented abstracts belong to the field of game theory and its applications to management. The abstract volume may be recommended for researches and post-graduate students of management, economic and applied mathematics departments. Computer design: Tatyana Grigorova and Andrey Zyatchin © Copyright of the authors, 2013 © SPbU, 2013 ТЕОРИЯ ИГР И МЕНЕДЖМЕНТ. Сборник тезисов 7-ой международной конференции по теории игр и менеджменту / Под ред. Л.А. Петросяна и Н.А. Зенкевича. – СПб.: Высшая школа менеджмента СПбГУ, 2013. – 274 с. Сборник содержит тезисы докладов участников 7-ой международной конференции по теории игр и менеджменту (26–28 июня 2013 года, Высшая школа менеджмента, Санкт-Петербургский государственный университет, Санкт- Петербург, Россия). Представленные тезисы относятся к теории игр и её приложениям в менеджменте. Тезисы представляют интерес для научных работников, аспирантов и студентов старших курсов университетов, специализирующихся по менеджменту, экономике и прикладной математике. Компьютерная верстка: Т.B. Григорова и А.В. Зятчин © Коллектив авторов, 2013 © СПбГУ, 2013 CONTENTS WELCOME ADDRESS.............................................................................................................. 9 WELCOME .................................................................................................................................10 One Guaranteed Search Problem on Trees.........................................................................12 Tatiana Abramovskaya Dynamic Stability of Strategic Alliances ..............................................................................14 Georgii Aleksandrov and Nikolay Zenkevich The Spec trum Value for Coalitional Games .......................................................................15 Mikel Álvarez-Mozos, Ziv Hellman and Eyal Winter Universal Nash Equilibrium for n-player Differential Games......................................18 Yurii Averboukh Pursuit-Evasion Game on the 1-skeleton of Regular Pol yhe dr ons ..............................21 Abdulla Azamov, Atamurat Kuchkarov and Azamat Holboyev On Gaming Situations that Simulate Partici pation in the Competition for a J ob....21 Abdulla Azamov and Abduhakim Mamanazarov Coordinating a Three-echelon Supply Chain with Uncertain Demand and Random Yield in Production ............................................28 Sudarshan Bardhan and Bibhas Chandra Giri Codes of Conduct and Bad Reputation ................................................................................30 Juan Block Intergenerational Solidarity within a Closing Pension Fund .........................................34 Tim Boonen, Anja De Waegenaere and Henk Norde Investments in R&D under Trade Liberalization: Monopolistic Competition Model ...........................................................................................37 Igor Bykadorov, Sergey Kokovin and Evgeny Zhelobodko Rewarding Idleness ....................................................................................................................41 Andrea Canidio and Thomas Gall A Coopetitive Game Theory Approach to Asymmetric R&D Alliances ....................46 David Carfì and Fabrizio Lanzafame The Effecti veness of Altruistic Lobbying: a Model Study ...............................................50 Pavel Chebotarev, Zoya Lezina, Anton Loginov and Yana Tsodikova A Weighted Deegan-Packel Social Capital Index ..............................................................54 Michela Chessa and Anna Khmelnitskaya Centr al Asian Gas in Eur asian Power Game ......................................................................56 Onur Cobanli Power in Game Theory .............................................................................................................59 Rodolfo Coelho Prates Dynamic Contests with Bankruptcy ......................................................................................61 Luis Corchon Love Game - Two S i de d Ma tchi ng .........................................................................................62 Suresh Deman Decompositions of Bbivariate Distributions, Areas of Random Triangles, and Bidding Games .............................................................64 Victor Domansky and Victoria Kreps A Matrix Approach to an Efficient Myerson Value on Union Stable Structures ....68 Hua Dong, Hao Sun, Genjiu Xu The Inverse Problem for Binomial Semivalues of Cooperative TU games................72 Irinel Dragan Consistency and the Core of Multi-Sided Assignment Markets ...................................73 Francesc Llerena, Marina Nunez and Carles Rafels Service Quality Level Choice on Oligopoly Competition ................................................76 Margarita Gladkova, Nikolay Zenkevich and Maria Kazantseva A Problem of Purpose Resource Use in the Two-Level Control Systems ...................78 Olga Gorbaneva and Gennady Ougolnitsky Multicriteria Coalitional Model of Decision-making over the Set of Projects with Constant Matrix of Payoffs in the Noncooperati ve Game ..............81 Xeniya Grigorieva and Pauline Shaikina Opti mal Contr ol of S IR Epi de mic Model wi th Virus Mutati ons .................................82 Elena Gubar and Quanyan Zhu Interaction Between Social Groups in Extended SIR Model..........................................85 Elena Gubar and Ekaterina Zhitkova Stochastic Bankruptcy Games ................................................................................................87 Helga Habis and P. Jean-Jacques Herings Communication and Coordination in Social Networks: Action as Communication Device. .........................................................................................89 Jia-Ping Huang, Maurice Koster and Ines Lindner Equilibrium in Secure Strategies in the Bertrand-Edge wor th Duopol y Model ........92 Mikhail Iskakov and Alexey Iskakov Resource Monotonic Allocations and the Core in Joint Investment Problems .........95 Josep Izquierdo and Carlos Rafels Comparison of the χ -value and the Shapley-value from an Economic Point of View with Respect to Fair Distribution of Collectively Earned Profits.......97 Susanne Jene and Stephan Zelewski Extensi ve Parti al Cooperati ve Game with Multi-Coalition Structure.........................99 Ji Zhihong, Gao Hongwei and Hu Jinsong Bargaining in Cooperative Games ...................................................................................... 100 Dominik Karos The Axiomatization of the Prenucleolus for Some Classes of Veto-Balanced Games........................................................................................................ 102 Ilya Katsev, Rene van Den Brink and Gerard van der Laan Overconfidence, Imperfect Competition, and Evolution .............................................. 103 Karen Khachatryan The Average Covering Tree Value for Directed Graph Games ................................ 104 Anna Khmelnitskaya, Ozer Selcuk and Dolf Talman The Shapley Value for TU Games with Oriented Graph Cooperation Structures...... 106 Anna Khmelnitskaya, Ozer Selcuk and Dolf Talman Two-Factor Model of Monopolistic Competi tion and Market Integration ............ 108 Sergey Kichko, Sergey Kokovin and Evgeny Zhelobodko Informed Middleman and Asymme tric Infor mati on..................................................... 111 Irina Kirysheva Generalized Model of “Vanishing Cities” ......................................................................... 112 Sergey Kokovin, Maxim Gorynov and Evgeny Zhelobodko The Relationship Between Discrete and Continuous Equilibria in Barg aining Model .............................................................................................................. 115 Aleksei Kondratev Application of Stochastic Cooperative Games in the Analysis of the Interaction of Economic Agents............................................................................... 117 Pavel Konyukhovskiy and Alexandra Malova Experiment with Efficient Groves-Ledyard Mechanism for Resource Allocation ...... 120 Galina Boldyreva, Nikolay Korgin and Vsevolod Korepanov Time Consistency of Strategic Alliances: Case Study Approach ............................... 122 Anastasia Koroleva Design and Implementation of Optimal Natural Resource Manage ment Sys te ms ............................................................................................................. 123 Serkan Kucuksenel Switching Lines for Optimal Feedback Control in Game of Two Pursuers against One Evader................................................................................. 125 Sergey Kumkov and Valerii Patsko An Axiomatization of the Nucleolus of Assignment Games ......................................... 128 Francesc Llerena, Marina Nunez and
Load more

Recommended publications
  • Pareto Optimality in Coalition Formation
    Pareto Optimality in Coalition Formation Haris Aziz NICTA and University of New South Wales, 2033 Sydney, Australia Felix Brandt∗ Technische Universit¨atM¨unchen,80538 M¨unchen,Germany Paul Harrenstein University of Oxford, Oxford OX1 3QD, United Kingdom Abstract A minimal requirement on allocative efficiency in the social sciences is Pareto op- timality. In this paper, we identify a close structural connection between Pareto optimality and perfection that has various algorithmic consequences for coali- tion formation. Based on this insight, we formulate the Preference Refinement Algorithm (PRA) which computes an individually rational and Pareto optimal outcome in hedonic coalition formation games. Our approach also leads to var- ious results for specific classes of hedonic games. In particular, we show that computing and verifying Pareto optimal partitions in general hedonic games, anonymous games, three-cyclic games, room-roommate games and B-hedonic games is intractable while both problems are tractable for roommate games, W-hedonic games, and house allocation with existing tenants. Keywords: Coalition Formation, Hedonic Games, Pareto Optimality, Computational Complexity JEL: C63, C70, C71, and C78 1. Introduction Ever since the publication of von Neumann and Morgenstern's Theory of Games and Economic Behavior in 1944, coalitions have played a central role within game theory. The crucial questions in coalitional game theory are which coalitions can be expected to form and how the members of coalitions should divide the proceeds of their cooperation. Traditionally the focus has been on the latter issue, which led to the formulation and analysis of concepts such as ∗Corresponding author Email addresses: [email protected] (Haris Aziz), [email protected] (Felix Brandt), [email protected] (Paul Harrenstein) Preprint submitted to Elsevier August 27, 2013 the core, the Shapley value, or the bargaining set.
    [Show full text]
  • A New IFORS Journal Is Born!
    Volume 16 | Number 1 | March 2021 | ISSN 2223-4373 International Federation of Operational Research Societies NEWS From the President What’s Inside 1 From the President A New IFORS journal is Born! Grazia Speranza Grazia Speranza <[email protected]> 2 From the Editor-in-Chief The International Transactions in Operational Sunity Shrestha Hada Research (ITOR) has been the flagship journal of IFORS since its launch in 1994. The journal has 2 OR Impact served the IFORS community for a number of years Transforming Food Production and with publishing the proceedings of conferences and Supply with OR/Analytics the biographies of key figures in the OR field, who now belong to the IFORS Hall of Fame (https://www. 6 OR and Development ifors.org/ifors-hall-of-fame/)The scientific editorial Disaster Mitigation: Leveraging world substantially evolved over time, furthermore Community Involvement to Improve the ITOR mission expanded and began to publish Water Access in sub-Saharan Africa high-quality scientific papers, capable of attracting citations. The initial goal for ITOR was to be indexed 9 Tutorial and then to increase the value of the key indicator of Integer Programming formulations the success of a journal, its impact factor. Thanks to the for the Vertex Coloring Problem commitment of the Editor-in-Chief, Celso Ribeiro, and the editorial board of the journal, year after year, ITOR has improved its impact factor (current 12 IFORS Award 2020 for OR in impact factor: 2.987 ) and has become one of the leading journals for the OR community. Development a) Optimal Investment Strategies In addition to a well-established flagship journal, a global society such as IFORS has to Minimize Flood Impact on Road the responsibility to introduce new ventures.
    [Show full text]
  • Pareto-Optimality in Cardinal Hedonic Games
    Research Paper AAMAS 2020, May 9–13, Auckland, New Zealand Pareto-Optimality in Cardinal Hedonic Games Martin Bullinger Technische Universität München München, Germany [email protected] ABSTRACT number of agents, and therefore it is desirable to consider expres- Pareto-optimality and individual rationality are among the most nat- sive, but succinctly representable classes of hedonic games. This ural requirements in coalition formation. We study classes of hedo- can be established by encoding preferences by means of a complete nic games with cardinal utilities that can be succinctly represented directed weighted graph where an edge weight EG ¹~º is a cardinal by means of complete weighted graphs, namely additively separable value or utility that agent G assigns to agent ~. Still, this underlying (ASHG), fractional (FHG), and modified fractional (MFHG) hedo- structure leaves significant freedom, how to obtain (cardinal) pref- nic games. Each of these can model different aspects of dividing a erences over coalitions. An especially appealing type of preferences society into groups. For all classes of games, we give algorithms is to have the sum of values of the other individuals as the value that find Pareto-optimal partitions under some natural restrictions. of a coalition. This constitutes the important class of additively While the output is also individually rational for modified fractional separable hedonic games (ASHGs) [6]. hedonic games, combining both notions is NP-hard for symmetric In ASHGs, an agent is willing to accept an additional agent into ASHGs and FHGs. In addition, we prove that welfare-optimal and her coalition as long as her valuation of this agent is non-negative Pareto-optimal partitions coincide for simple, symmetric MFHGs, and in this sense, ASHGs are not sensitive to the intensities of single- solving an open problem from Elkind et al.
    [Show full text]
  • Code De Conduite Pour Le Water Polo
    HistoFINA SWIMMING MEDALLISTS AND STATISTICS AT OLYMPIC GAMES Last updated in November, 2016 (After the Rio 2016 Olympic Games) Fédération Internationale de Natation Ch. De Bellevue 24a/24b – 1005 Lausanne – Switzerland TEL: (41-21) 310 47 10 – FAX: (41-21) 312 66 10 – E-mail: [email protected] Website: www.fina.org Copyright FINA, Lausanne 2013 In memory of Jean-Louis Meuret CONTENTS OLYMPIC GAMES Swimming – 1896-2012 Introduction 3 Olympic Games dates, sites, number of victories by National Federations (NF) and on the podiums 4 1896 – 2016 – From Athens to Rio 6 Olympic Gold Medals & Olympic Champions by Country 21 MEN’S EVENTS – Podiums and statistics 22 WOMEN’S EVENTS – Podiums and statistics 82 FINA Members and Country Codes 136 2 Introduction In the following study you will find the statistics of the swimming events at the Olympic Games held since 1896 (under the umbrella of FINA since 1912) as well as the podiums and number of medals obtained by National Federation. You will also find the standings of the first three places in all events for men and women at the Olympic Games followed by several classifications which are listed either by the number of titles or medals by swimmer or National Federation. It should be noted that these standings only have an historical aim but no sport signification because the comparison between the achievements of swimmers of different generations is always unfair for several reasons: 1. The period of time. The Olympic Games were not organised in 1916, 1940 and 1944 2. The evolution of the programme.
    [Show full text]
  • Optimizing Expected Utility and Stability in Role Based Hedonic Games
    Proceedings of the Thirtieth International Florida Artificial Intelligence Research Society Conference Optimizing Expected Utility and Stability in Role Based Hedonic Games Matthew Spradling University of Michigan - Flint mjspra@umflint.edu Abstract Table 1: Ex. RBHG instance with |P | =4,R= {A, B} In the hedonic coalition formation game model Roles Based r, c u (r, c) u (r, c) u (r, c) u (r, c) Hedonic Games (RBHG), agents view teams as compositions p0 p1 p2 p3 of available roles. An agent’s utility for a partition is based A, AA 2200 upon which roles she and her teammates fulfill within the A, AB 0322 coalition. I show positive results for finding optimal or sta- B,AB 3033 ble role matchings given a partitioning into teams. In set- B,BB 1111 tings such as massively multiplayer online games, a central authority assigns agents to teams but not necessarily to roles within them. For such settings, I consider the problems of op- timizing expected utility and expected stability in RBHG. I As per (Spradling and Goldsmith 2015), a Role Based He- show that the related optimization problems for partitioning donic Game (RBHG) instance consists of: are NP-hard. I introduce a local search heuristic method for • P approximating such solutions. I validate the heuristic by com- : A population of players parison to existing partitioning approaches using real-world • R: A set of roles data scraped from League of Legends games. • C: A set of compositions, where a composition c ∈ C is a multiset (bag) of roles from R. Introduction • U : P × R × C → Z defines the utility function ui(r, c) In coalition formation games, agents from a population have for each player pi.
    [Show full text]
  • The Dynamics of Europe's Political Economy
    Die approbierte Originalversion dieser Dissertation ist in der Hauptbibliothek der Technischen Universität Wien aufgestellt und zugänglich. http://www.ub.tuwien.ac.at The approved original version of this thesis is available at the main library of the Vienna University of Technology. http://www.ub.tuwien.ac.at/eng DISSERTATION The Dynamics of Europe’s Political Economy: a game theoretical analysis Ausgeführt zum Zwecke der Erlangung des akademischen Grades einer Doktorin der Sozial- und Wirtschaftswissenschaften unter der Leitung von Univ.-Prof. Dr. Hardy Hanappi Institut für Stochastik und Wirtschaftsmathematik (E105) Forschunggruppe Ökonomie Univ.-Prof. Dr. Pasquale Tridico Institut für Volkswirtschaftslehre, Universität Roma Tre eingereicht an der Technischen Universität Wien Fakultät für Mathematik und Geoinformation von Mag. Gizem Yildirim Matrikelnummer: 0527237 Hohlweggasse 10/10, 1030 Wien Wien am Mai 2017 Acknowledgements I would like to thank Professor Hardy Hanappi for his guidance, motivation and patience. I am grateful for inspirations from many conversations we had. He was always very generous with his time and I had a great freedom in my research. I also would like to thank Professor Pasquale Tridico for his interest in my work and valuable feedbacks. The support from my family and friends are immeasurable. I thank my parents and my brother for their unconditional and unending love and support. I am incredibly lucky to have great friends. I owe a tremendous debt of gratitude to Sarah Dippenaar, Katharina Schigutt and Markus Wallerberger for their support during my thesis but more importantly for sharing good and bad times. I also would like to thank Gregor Kasieczka for introducing me to jet clustering algorithms and his valuable suggestions.
    [Show full text]
  • Fractional Hedonic Games
    Fractional Hedonic Games HARIS AZIZ, Data61, CSIRO and UNSW Australia FLORIAN BRANDL, Technical University of Munich FELIX BRANDT, Technical University of Munich PAUL HARRENSTEIN, University of Oxford MARTIN OLSEN, Aarhus University DOMINIK PETERS, University of Oxford The work we present in this paper initiated the formal study of fractional hedonic games, coalition formation games in which the utility of a player is the average value he ascribes to the members of his coalition. Among other settings, this covers situations in which players only distinguish between friends and non-friends and desire to be in a coalition in which the fraction of friends is maximal. Fractional hedonic games thus not only constitute a natural class of succinctly representable coalition formation games, but also provide an interesting framework for network clustering. We propose a number of conditions under which the core of fractional hedonic games is non-empty and provide algorithms for computing a core stable outcome. By contrast, we show that the core may be empty in other cases, and that it is computationally hard in general to decide non-emptiness of the core. 1 INTRODUCTION Hedonic games present a natural and versatile framework to study the formal aspects of coalition formation which has received much attention from both an economic and an algorithmic perspective. This work was initiated by Drèze and Greenberg[1980], Banerjee et al . [2001], Cechlárová and Romero-Medina[2001], and Bogomolnaia and Jackson[2002] and has sparked a lot of follow- up work. A recent survey was provided by Aziz and Savani[2016]. In hedonic games, coalition formation is approached from a game-theoretic angle.
    [Show full text]
  • Pareto Optimality in Coalition Formation
    Pareto Optimality in Coalition Formation Haris Aziz Felix Brandt Paul Harrenstein Technische Universität München IJCAI Workshop on Social Choice and Artificial Intelligence, July 16, 2011 1 / 21 Coalition formation “Coalition formation is of fundamental importance in a wide variety of social, economic, and political problems, ranging from communication and trade to legislative voting. As such, there is much about the formation of coalitions that deserves study.” A. Bogomolnaia and M. O. Jackson. The stability of hedonic coalition structures. Games and Economic Behavior. 2002. 2 / 21 Coalition formation 3 / 21 Hedonic Games A hedonic game is a pair (N; ) where N is a set of players and = (1;:::; jNj) is a preference profile which specifies for each player i 2 N his preference over coalitions he is a member of. For each player i 2 N, i is reflexive, complete and transitive. A partition π is a partition of players N into disjoint coalitions. A player’s appreciation of a coalition structure (partition) only depends on the coalition he is a member of and not on how the remaining players are grouped. 4 / 21 Classes of Hedonic Games Unacceptable coalition: player would rather be alone. General hedonic games: preference of each player over acceptable coalitions 1: f1; 2; 3g ; f1; 2g ; f1; 3gjf 1gk 2: f1; 2gjf 1; 2; 3g ; f1; 3g ; f2gk 3: f2; 3gjf 3gkf 1; 2; 3g ; f1; 3g Partition ff1g; f2; 3gg 5 / 21 Classes of Hedonic Games General hedonic games: preference of each player over acceptable coalitions Preferences over players extend to preferences over coalitions Roommate games: only coalitions of size 1 and 2 are acceptable.
    [Show full text]
  • 15 Hedonic Games Haris Azizaand Rahul Savanib
    Draft { December 5, 2014 15 Hedonic Games Haris Azizaand Rahul Savanib 15.1 Introduction Coalitions are a central part of economic, political, and social life, and coalition formation has been studied extensively within the mathematical social sciences. Agents (be they humans, robots, or software agents) have preferences over coalitions and, based on these preferences, it is natural to ask which coalitions are expected to form, and which coalition structures are better social outcomes. In this chapter, we consider coalition formation games with hedonic preferences, or simply hedonic games. The outcome of a coalition formation game is a partitioning of the agents into disjoint coalitions, which we will refer to synonymously as a partition or coalition structure. The defining feature of hedonic preferences is that every agent only cares about which agents are in its coalition, but does not care how agents in other coali- tions are grouped together (Dr`ezeand Greenberg, 1980). Thus, hedonic preferences completely ignore inter-coalitional dependencies. Despite their relative simplicity, hedonic games have been used to model many interesting settings, such as research team formation (Alcalde and Revilla, 2004), scheduling group activities (Darmann et al., 2012), formation of coalition governments (Le Breton et al., 2008), cluster- ings in social networks (see e.g., Aziz et al., 2014b; McSweeney et al., 2014; Olsen, 2009), and distributed task allocation for wireless agents (Saad et al., 2011). Before we give a formal definition of a hedonic game, we give a standard hedonic game from the literature that we will use as a running example (see e.g., Banerjee et al.
    [Show full text]
  • International Conference on Game Theory and Management” (GTM2020)
    The 14th International Conference on Game Theory and Management” (GTM2020) 05-09 October 2020 Saint Petersburg, Russia Organized by Saint Petersburg State University and The International Society of Dynamic Games Saint Petersburg State University Volkhovsky per., 3, St. Petersburg, Russia Program Committee Leon Petrosyan (Russia) – co-chair; Nikolay Zenkevich (Russia) – co-chair; Eitan Altman (France); Abdulla Azamov (Uzbekistan); Jesus Mario Bilbao (Spain); Irinel Dragan (USA); Hongwei Gao (China); Andrey Garnaev (USA); Sergiu Hart (Israel); Steffen Jørgensen (Denmark); Ehud Kalai (USA); Andrea Di Liddo (Italy); Vladimir Mazalov (Russia); Shigeo Muto (Japan); Richard Staelin (USA); Krzysztof Szajowski (Poland); Agnieszka Wiszniewska-Matyszkie (Poland); Myrna Wooders (UK); David W.K. Yeung (Hong Kong); Georges Zaccour (Canada); Paul Zipkin (USA) Program Saint Petersburg State University, St. Petersburg, Russia Monday, October 05 16:45–17:00 WELCOME ADDRESS 17:00–18:00 PLENARY TALK (1) 18:10–19:50 PARALLEL SESSIONS (M1) Tuesday, October 06 10:00–11:00 PLENARY TALK (2) 11:10–12:50 PARALLEL SESSIONS (T1) 17:00–19:30 PARALLEL SESSIONS (T2) Wednesday, October 07 10:00–11:00 PLENARY TALK (3) 11:10–13:15 PARALLEL SESSIONS (W1) 17:00–19:30 PARALLEL SESSIONS (W2) Thursday, October 08 10:00–12:55 PARALLEL SESSIONS (T1) 17:00–18:00 PLENARY TALK (4) 18:10–19:50 PARALLEL SESSIONS (T2) Friday, October 09 10:00–12:30 PARALLEL SESSIONS (F1) 12:40–13:00 CLOSING SESSION 2 Monday, October 05 16:45–17:00 WELCOME ADDRESS Co-chairs – Leon Petrosyan and Nikolay
    [Show full text]
  • Len European Championships Aquatic Finalists
    LEN EUROPEAN CHAMPIONSHIPS AQUATIC FINALISTS 1926-2016 2 EUROPEAN CHAMPIONSHIPS GLASGOW 2ND-12TH AUGUST 2018 SWIMMING AT TOLLCROSS INTERNATIONAL SWIMMING CENTRE DIVING AT ROYAL COMMONWEALTH POOL, EDINBURGH ARTISTIC (SYNCHRONISED) SWIMMING AT SCOTSTOUN SPORTS CAMPUS, GLASGOW OPEN WATER SWIMMING IN LAKE LOMOND 2 Contents Event Page Event Page European Championship Venues 5 4x100m Freestyle Team- Mixed 123 4x100m Medley Team – Mixed 123 50m Freestyle – Men 7 100m Freestyle – Men 9 Open Water Swimming – Medals Table 124 200m Freestyle – Men 13 400m Freestyle – Men 16 5km Open Water Swimming – Men 125 800m Freestyle – Men 20 10km Open Water Swimming – Men 126 1500m Freestyle – Men 21 25km Open Water Swimming – Men 127 50m Backstroke – Men 25 5km Open Water Swimming – Women 129 100m Backstroke – Men 26 10km Open Water Swimming – Women 132 200m Backstroke – Men 30 25km Open Water Swimming – Women 133 50m Breaststroke – Men 34 Open Water Swimming – Team 5km Race 136 100m Breaststroke – Men 35 200m Breaststroke – Men 38 Diving – Medals Table 137 50m Butterfly – Men 43 1m Springboard – Men 138 100m Butterfly – Men 44 3m Springboard – Men 140 200m Butterfly – Men 47 3m Springboard Synchro - Men 143 10m Platform – Men 145 200m Individual Medley – Men 50 10m Platform Synchro – Men 148 400m Individual Medley – Men 54 1m Springboard – Women 150 4x100m Freestyle Team – Men 58 3m Springboard – Women 152 4x200m Freestyle Team – Men 61 3m Springboard Synchro – Women 155 4x100m Medley Team – Men 65 10m Platform – Women 158 10m Platform Synchro – Women 161
    [Show full text]
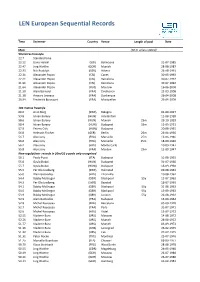
  • LEN European Sequential Records
    LEN European Sequential Records Time Swimmer Country Venue Length of pool Date Men: (50 m unless stated) 50 metres freestyle 22.7 Standard time 22.52 Dano Halsall (SUI) Bellinzona 21-07-1985 22.47 Jorg Woithe (GDR) Munich 28-08-1987 22.33 Nils Rudolph (GER) Athens 24-08-1991 22.31 Alexander Popov (CSI) Canet 30-05-1992 22.21 Alexander Popov (CSI) Barcelona 30-07-1992 21.91 Alexander Popov (CSI) Barcelona 30-07-1992 21.64 Alexander Popov (RUS) Moscow 16-06-2000 21.50 Alain Bernard (FRA) Eindhoven 23-03-2008 21.38 Amaury Leveaux (FRA) Dunkerque 26-04-2008 20.94 Frederick Bousquet (FRA) Montpellier 26-04-2009 100 metres freestyle 60.0 Arne Borg (SWE) Bologna 04-09-1927 59.8 Istvan Barany (HUN) Amsterdam 11-08-1928 58.6 Istvan Barany (HUN) Munich 25m 29-10-1929 58.4 Istvan Barany (HUN) Budapest 33m 12-05-1931 57.8 Ferenc Csik (HUN) Budapest 20-08-1935 56.8 Helmuth Fischer (GER) Berlin 25m 26-04-1936 56.7 Alex Jany (FRA) Marseille 25m 12-06-1946 56.6 Alex Jany (FRA) Marseille 25m 18-09-1946 56.2 Alex Jany (FRA) Monte Carlo 10-09-1947 55.8 Alex Jany (FRA) Menton 25m 15-09-1947 New regulations- records in 50m/55 y pools only recognised 56.1 Paolo Pucci (ITA) Budapest 31-08-1955 55.8 Gyula Dobai (HUN) Budapest 31-07-1960 55.7 Gyula Dobai (HUN)) Budapest 18-09-1960 55.5 Per Ola Lindberg (SWE) Halmstad 09-08-1961 55.0 Alain Gottvalles (FRA) Thionville 10-08-1962 54.4 Bobby McGregor (GBR) Blackpool 55y 13-07-1963 54.3 Per Ola Lindberg (SWE) Baastad 18-07-1963 54.1 Bobby McGregor (GBR) Blackpool 55y 31-08-1963 54.0 Bobby McGregor (GBR) Blackpool 55y
    [Show full text]