STUDY on the FRAGMENTATION of SHELLS Falk K. Wittel1, Ferenc
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Explosive Weapon Effectsweapon Overview Effects
CHARACTERISATION OF EXPLOSIVE WEAPONS EXPLOSIVEEXPLOSIVE WEAPON EFFECTSWEAPON OVERVIEW EFFECTS FINAL REPORT ABOUT THE GICHD AND THE PROJECT The Geneva International Centre for Humanitarian Demining (GICHD) is an expert organisation working to reduce the impact of mines, cluster munitions and other explosive hazards, in close partnership with states, the UN and other human security actors. Based at the Maison de la paix in Geneva, the GICHD employs around 55 staff from over 15 countries with unique expertise and knowledge. Our work is made possible by core contributions, project funding and in-kind support from more than 20 governments and organisations. Motivated by its strategic goal to improve human security and equipped with subject expertise in explosive hazards, the GICHD launched a research project to characterise explosive weapons. The GICHD perceives the debate on explosive weapons in populated areas (EWIPA) as an important humanitarian issue. The aim of this research into explosive weapons characteristics and their immediate, destructive effects on humans and structures, is to help inform the ongoing discussions on EWIPA, intended to reduce harm to civilians. The intention of the research is not to discuss the moral, political or legal implications of using explosive weapon systems in populated areas, but to examine their characteristics, effects and use from a technical perspective. The research project started in January 2015 and was guided and advised by a group of 18 international experts dealing with weapons-related research and practitioners who address the implications of explosive weapons in the humanitarian, policy, advocacy and legal fields. This report and its annexes integrate the research efforts of the characterisation of explosive weapons (CEW) project in 2015-2016 and make reference to key information sources in this domain. -

Fighting Vehicle Technology
Fighting Vehicle Technology 41496_DSTA 60-77#150Q.indd 1 5/6/10 12:44 AM ABSTRACT Armoured vehicle technology has evolved ever since the first tanks appeared in World War One. The traditional Armoured Fighting Vehicle (AFV) design focuses on lethality, survivability and mobility. However, with the growing reliance on communications and command (C2) systems, there is an increased need for the AFV design to be integrated with the vehicle electronics, or vetronics. Vetronics has become a key component of the AFV’s effectiveness on the battlefield. An overview of the technology advances in these areas will be explored. In addition, the impact on the human aspect as a result of these C2 considerations will be covered. Tan Chuan-Yean Mok Shao Hong Vince Yew 41496_DSTA 60-77#150Q.indd 2 5/6/10 12:44 AM Fighting Vehicle Technology 62 and more advanced sub-systems will raise the INTRODUCTION question of how the modern crew is able to process and use the information effectively. On the modern battlefield, armies are moving towards Network-Centric Warfare TECHNOLOGIES IN AN (NCW). Forces no longer fight as individual entities but as part of a larger system. Each AFV entity becomes a node in a network where information can be shared, and firepower can Firepower be called upon request. AFVs are usually equipped with weapon Key to this network fighting capability is the stations for self-protection and the communications and command (C2) system. engagement of targets. Depending on By enabling each force to be plugged into the threat, some are equipped with pintle the C2 system, information can be shared mount systems for light weapons (e.g. -

Narco Armor: Improvised Armored Fighting Vehicles in Mexico Robert J
Claremont Colleges Scholarship @ Claremont CGU Faculty Publications and Research CGU Faculty Scholarship 1-1-2013 Narco Armor: Improvised Armored Fighting Vehicles in Mexico Robert J. Bunker Claremont Graduate University Byron Ramirez Claremont Graduate University Recommended Citation Bunker, R.J. & Ramirez, B. (Eds.). (2013). Narco Armor: Improvised Armored Fighting Vehicles in Mexico. Fort Leavenworth, KS: The orF eign Military Studies Office. This Report is brought to you for free and open access by the CGU Faculty Scholarship at Scholarship @ Claremont. It has been accepted for inclusion in CGU Faculty Publications and Research by an authorized administrator of Scholarship @ Claremont. For more information, please contact [email protected]. WL KNO EDGE NCE ISM SA ER IS E A TE N K N O K C E N N T N I S E S J E N A 3 V H A A N H Z И O E P W O I T E D N E Z I A M I C O N O C C I O T N S H O E L C A I N M Z E N O T Narco Armor Improvised Armored Fighting Vehicles in Mexico Robert J. Bunker and Byron Ramirez, Editors In cooperation with Borderland Beat, InSight Crime, & Small Wars Journal— El Centro Open Source, Foreign Perspective, Underconsidered/Understudied Topics The Foreign Military Studies Office (FMSO) at Fort Leavenworth, Kansas, is an open source research organization of the U.S. Army. It was founded in 1986 as an innovative program that brought together military specialists and civilian academics to focus on military and security topics derived from unclassified, foreign media. -

M67 IM Hand Grenade Unique Safety Features for Improved Operation, Safe Storage and Transit
ELBIT SYSTEMS - LAND INFANTRY M67 IM Hand Grenade Unique safety features for improved operation, safe storage and transit The M67 IM - HE fragmentation grenade offers enhanced safety features and improved operational reliability. A unique fuze with a safety and arming (S&A) mechanism enables safer storage and transportation with fewer restrictions. Improved safety: The M67 IM is equipped with a unique safety clip that provides enhanced protection against unintentional safety pin damage. The grenade requires two movement factors for removal of the safety pin, and includes peripheral protection on the fuze housing. The grenade offers the option of an additional thumb clip. In compliance with the latest safety requirements for fuzes-MIL-STD 1316 and for Insensitive Munitions (IM) MIL-STD 2015, the M67 IM hand grenade delivers a bullet impact of 0.5” , Fast Cook - off (bare and packed), Slow Cook- off ( bare and packed) and sympathetic detonation . Initiation of the detonation chain sets off an audible bang. Operational reliability: The M67 IM is similar in lethality, handling operation, and dimensions to the basic M67 grenade. M67 IM Hand Grenade Unique safety features for improved operation, safe storage and transit Key Features Key Benefits • Weight: 400gr • Best-in-class safety features • Height: 91mm • Safer transit and storage • Filling: 185gr Comp.B • MIL-STD 1316 and MIL-STD 2105 • Diameter: 64mm • Dangerous Goods Classification 1.1D (can upgrade to 1.6 in accordance with client request) • Delay time: 4.5 ± 0.5 sec EP19-MKT-012 Grenade after Grenade after 0.5” M20 (APIT) SCO test bullet impact Elbit Systems Land E-mail: [email protected] www.elbitsystems.com Follow us on The logo brand, product, service, and process names appearing herein are the trademarks or service marks of Elbit Systems Ltd., its affiliated companies or, where applicable, of other respective holders. -

Patent Application Publication (10) Pub. No.: US 2017/0122713 A1 Greenw00d (43) Pub
US 2017.0122713A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2017/0122713 A1 GreenW00d (43) Pub. Date: May 4, 2017 (54) APPARATUS AND SYSTEM TO COUNTER F4A 2L/32 (2006.01) DRONES USING SEM-GUIDED F4H II/02 (2006.01) FRAGMENTATION ROUNDS F4IG 3/06 (2006.01) F42C 17/04 (2006.01) (71) Applicant: Martin William Greenwood, Poway, (52) U.S. Cl. CA (US) CPC ................ F42B 12/22 (2013.01); F4IG 3/06 O O (2013.01); F42C 9/00 (2013.01); F42C 17/04 (72) Inventor: Martin William Greenwood, Poway, (2013.01); F4A 2L/32 (2013.01); F4H II/02 CA (US) (2013.01); F42B 12/205 (2013.01) (21) Appl. No.: 14/932,854 (57) ABSTRACT (22) Filed: Nov. 4, 2015 Abattlefield weapon system is proposed to counter the threat 9 posed by small drones. The system uses a standard .50 O O caliber machine gun firing explosive rounds, to create a flak Publication Classification bombardment to bring down the drone. A control system (51) Int. Cl. causes the round to fragment as it approaches the range of F42B (2/22 (2006.01) the target. The direction in which the round is fired is F42C 9/00 (2006.01) controlled manually by the gunner. The system is fully F42B (2/20 (2006.01) portable for dispersed deployment among infantry. - - - - - - - - - / / - Patent Application Publication May 4, 2017. Sheet 1 of 4 US 2017/O122713 A1 Figure 1. Patent Application Publication May 4, 2017. Sheet 2 of 4 US 2017/O122713 A1 Figure 2. Patent Application Publication May 4, 2017. -

Understanding Explosive Weapons with Wide Area Effects
Areas of harm Understanding explosive weapons with wide area effects www.paxforpeace.nl Colophon October 2016 ISBN 978-94-92487-05-6/NUR 689 Serial number PAX 2016/10 Cover photo: Aleppo, Syria - 2013. A building destroyed by repeated shelling, residents have tried to keep their business on the ground foor running. © Hannah Lucinda Smith About Article 36 Article 36 is a UK-based not-for-proft organisation working to prevent the unintended, unnecessary or unacceptable harm caused by certain weapons. Article 36 undertakes research, policy and advocacy and promotes civil society partnerships to respond to harm caused by existing weapons and to build a stronger framework to prevent harm as weapons are used or developed in the future. www.article36.org About PAX PAX means peace. Together with people in confict areas and concerned citizens worldwide, PAX works to build just and peaceful societies across the globe. PAX brings together people who have the courage to stand for peace. Everyone who believes in peace can contribute. We believe that all these steps, whether small or large, inevitably lead to the greater sum of peace. www.paxforpeace.nl For additional information, please contact [email protected]. We would like to thank Colin King for his input and advice. 2 PAX / Article 36 ! Areas of Harm Content Summary & recommendations 4 Introduction 6 Part 1: Wide area effects 8 Large blast and fragmentation radius 9 Inaccuracy of delivery 12 Use of multiple warheads or multiple frings 19 Additional factors that determine area effects 21 Conclusion -
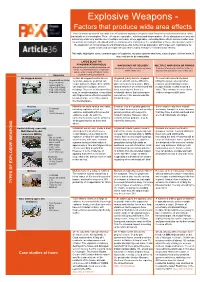
Explosive Weapons
Explosive Weapons - Factors that produce wide area effects There is broad agreement that wide area effects from explosive weapons result from three main characteristics, either individually or in combination. These effects are cumulative, with blast and fragmentation effects always present and with inaccuracy of delivery and the use of multiple warheads, where applicable, extending those effects across a wider area. As well as increasing the likelihood of direct civilian deaths and injuries, the combination of these effects also results in the destruction of civilian property and infrastructure vital to the civilian population, with longer-term implications for public health and development (sometimes called ‘tertiary’ or ‘reverberating’ effects). This table highlights some common types of explosive weapon systems that have caused grave civilian harm. It does not aim to be exhaustive. LARGE BLAST OR FRAGMENTATION RADIUS INACCURACY OF DELIVERY MULTIPLE WARHEADS OR FIRINGS A large amount of explosive substance can An explosive munition may land anywhere A number of explosive munitions is fired or create a powerful blast wave. Fragments within a wide area released and spreads to cover a wide area (pieces of the casing and debris) can be Examples projected over a long distance Air-dropped bombs Certain air-dropped bombs have a Unguided gravity bombs, dropped To counteract uncertainty about • Unguided Mk82 (500lb) very high explosive yield that can from an aircraft, can be difficult to hitting the target, amongst other • BLU-117 (Mk84) create a powerful blast effect, which place accurately on a target. Many reasons, an aircraft may release • Guided GBU-12 • GBU-43/B (MOAB) can lead to the collapse of entire factors influence where the bomb will multiple bombs in what is called a • FAB-1500 (3307lb) buildings. -

Lethal Influence Factors of Natural and Preformed Fragmentation Projectiles
DAAAM INTERNATIONAL SCIENTIFIC BOOK 2015 pp. 219-234 Chapter 20 LETHAL INFLUENCE FACTORS OF NATURAL AND PREFORMED FRAGMENTATION PROJECTILES ZECEVIC, B.; TERZIC, J.; RAZIC, F. & SERDAREVIC-KADIC, S. Abstract: Low intensity warfare had many impact on reducing logistic costs during field operations. It influenced the development of new large caliber HE projectiles. Concerning increasing lethal efficiency at target, the focus is at development of modern projectiles with natural, embossed and preformed fragmentation. Modern natural fragmentation projectiles characterize excellent aerodynamic properties, use of high strength steel with high fragmentation characteristics and denser high energy materials. Artillery projectiles with preformed fragments are usually equipped with large amount of preformed spherical or cubical fragments made of steel or tungsten. Modern unguided rocket warheads are based on embossed fragmentation or preformed warheads concept. There are limited data about real lethal effects of these projectiles. This paper presents available data and research results of embossed fragmentation warhead 122 mm and prefragmented warhead 128 mm, which are conducted in Bosnia and Herzegovina. Key words: projectile, lethal, warhead, prefragmented, rocket Authors´ data: Prof. Dr. Sc. Zecevic, B[erko]; Assist. Prof. Dr. Sc. Terzic, J[asmin], Senior Assistant Razic F[aruk], Assist. Prof. Dr. Sc. Serdarevic-Kadic S[abina] Faculty of Mechanical Engineering, University of Sarajevo, Vilsonovo setaliste 9, Sarajevo 71000, Bosnia and Herzegovina, [email protected], [email protected], [email protected], [email protected]. This Publication has to be referred as: Zecevic, B[erko]; Terzic, J[asmin]; Razic, F[aruk] & Serdarevic-Kadic, S[abina] (2015). Lethal Influence Factors of Natural and Preformed Fragmentation Projectiles, Chapter 20 in DAAAM International Scientific Book 2015, pp.219-234, B. -

Acceleration Characteristics of Discrete Fragments Generated from Explosively-Driven Cylindrical Metal Shells
materials Article Acceleration Characteristics of Discrete Fragments Generated from Explosively-Driven Cylindrical Metal Shells Mingxue Zhou , Cheng Wu *, Fengjiang An, Shasha Liao, Xiaoxia Yuan , Dongyu Xue and Jian Liu State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China; [email protected] (M.Z.); [email protected] (F.A.); [email protected] (S.L.); [email protected] (X.Y.); [email protected] (D.X.); [email protected] (J.L.) * Correspondence: [email protected]; Tel.: +86-01068915677 Received: 22 March 2020; Accepted: 26 April 2020; Published: 30 April 2020 Abstract: The acceleration characteristics of fragments generated from explosively-driven cylindrical shells are important issues in warhead design. However, there is as yet no reasonable theory for predicting the acceleration process of a specific metallic shell; existing approaches either ignore the effects of shell disintegration and the subsequent gas leakage on fragment acceleration or treat them in a simplified manner. In this paper, a theoretical model was established to study the acceleration of discrete fragments under the combined effect of shell disintegration and gas leakage. Firstly, an equation of motion was developed, where the acceleration of a cylindrical shell and the internal detonation gas was determined by the motive force impacting the inner surface of the metallic cylinder. To account for the force decrease induced by both the change in fragment area after the shell disintegrates and the subsequent drop in gas pressure due to gas leakage, the equation of motion was then associated with an equation for the locally isentropic expansion of the detonation gas and a modified gas-leakage equation. -

Tank Platoon
ATP 3-20.15 (FM 3-20.15) Tank Platoon December 2012 DISTRIBUTION RESTRICTION: Approved for public release; distribution is unlimited. Headquarters, Department of the Army This publication is available at Army Knowledge Online (https//armypubs.us.army.mil/doctrine/ index.html). *ATP 3-20.15 (FM 3-20.15) Army Techniques and Procedures Headquarters No. 3-20.15 Department of the Army Washington, DC, 13 December 2012 Tank Platoon Contents Page PREFACE .................................................................... viii Chapter 1 TACTICAL FUNDAMENTALS ..................................... 1-1 Section I – Text References ....................................... 1-1 Section II – Overview.................................................. 1-1 Operational Environment .............................................. 1-1 Unified Land Operations ............................................... 1-2 Combat Power .............................................................. 1-2 Section III – Mission Command ................................. 1-4 Command ..................................................................... 1-4 Control .......................................................................... 1-5 Section IV – Command and Support Relationships .............................................................. 1-6 Command Relationships .............................................. 1-6 Support Relationships .................................................. 1-7 Section V – Planning Considerations ....................... 1-7 Operational Variables -

The Hand Grenade Gordon L
THE HAND GRENADE GORDON L. ROTTMAN © Osprey Publishing • www.ospreypublishing.com THE HAND GRENADE GORDON L. ROTTMAN Series Editor Martin Pegler © Osprey Publishing • www.ospreypublishing.com CONTENTS INTRODUCTION 4 DEVELOPMENT 7 A universal weapon USE 35 Grenades in combat IMPACT 62 Assessing the hand grenade’s influence CONCLUSION 75 GLOSSARY 77 BIBLIOGRAPHY 79 INDEX 80 © Osprey Publishing • www.ospreypublishing.com INTRODUCTION The hand grenade is essentially a technologically enhanced improvement of what was the first multifunctional, direct- and indirect-fire, offensive A German Handgranatetrupp weapon employed in warfare – the rock. The hand grenade is basically a (hand-grenade team) rushes small missile filled with an HE or chemical agent intended for hand across no man’s land with each delivery against enemy personnel or material at short ranges. Over time man carrying a pair of hand- such weapons have been supplemented by special-purpose grenades, grenade bags under his arms, 1917. The rightmost man carries a which dispense irritant gas, incendiary effects, smoke screening, signaling, stick grenade in his hand. They or target marking. The most utilitarian grenades are high-explosive/ are armed with Mauser 7.92mm fragmentation (HE/frag or simply “frags”) – “casualty-producing” Kar 98A carbines rather than the antipersonnel weapons. These are referred to as “defensive” grenades as longer Gew 98 rifles carried by other German infantrymen. (Tom they are intended to be thrown from behind cover. Another casualty- Laemlein/Armor Plate Press) producing grenade is the blast, concussion, or “offensive” grenade. These 4 © Osprey Publishing • www.ospreypublishing.com have bodies made of thin, light materials generating little fragmentation. -

The Future Combat System: Minimizing Risk While Maximizing Capability
The Future Combat System: Minimizing Risk While Maximizing Capability USAWC Strategy Research Project by Colonel Brian R. Zahn, USA May 2000 Working Paper 00 – 2 The views expressed in this academic research paper are those of the author and do not necessarily reflect the official policy or position of the U.S. Government, the Department of Defense, or any of its agencies. ABSTRACT AUTHOR: Colonel Brian R. Zahn TITLE: The Future Combat System: Minimizing Risk While Maximizing Capability FORMAT: Strategy Research Project DATE: 24 April 2000 PAGES: 45 CLASSIFICATION: Unclassified This paper examines some of the technological candidates that are potential enablers of the Army Transformation to the future Objective Force. The paper highlights the technological risk associated with the Future Combat System program and offers an alternative acquisition strategy to minimize risk while maximizing potential capability. The paper examines lethality technologies such as the electromagnetic gun, electrothermal chemical gun, missile-in-a- box, and compact kinetic energy missile. Survivability candidates include passive armors, reactive armors, and active protection systems. The paper also examines the wheeled versus tracked debate. The paper concludes by recommending some of the technologies for further development under a parallel acquisition strategy. 2 TABLE OF CONTENTS ABSTRACT.......................................................................................................................................................................III