DISSERTATION High Performance Computing In
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

DIBOL for Beginners Order No
DIBOL for Beginners Order No. AA-BI77 A-TK April 1984 Supersession: This is a new manual. Operating System: VAXNMS, CTS-300, RSTS/E, Professional, RSX-11 M-Plus, Micro/RSX, Professional CTS-300 Software Version: Applicable to all products containing DIBOL-83 . First Printing, April 1984 The information in this document is subject to change without notice and should not be construed as a commitment by Digital Equipment Corporation. Digital Equipment Corporation assumes no responsibility for any errors that may appear in this document. The software described in this document is furnished under a license and may only be used or copied in accordance with the terms of such license. No responsibility is assumed for the use or reliability of software on equipment that is not supplied by DIGITAL or its affiliated companies. The specifications and drawings, herein, are the property of Digital Equipment Corporation and shall not be reproduced or copied or used in whole or in part as the basis for the manufacture or sale of items without written permission. Copyright © 1984 by Digital Equipment Corporation. All Rights Reserved The following are trademarks of Digital Equipment Corporation: CTI BUS MASSBUS RSTS DEC PDP RSX DECmate P/OS Tool Kit DECsystem-10 PRO/BASIC UNIBUS DECSYSTEM-20 Professional VAX DECUS PRO/FMS VMS DECwriter PRO/RMS VT DIBOL PROSE Work Processor mamDOma Rainbow CONTENTS Page PREFACE ............................................................................................. v INTRODUCTION ...................................................................... Introduction-1 CHAPTER 1 COMMUNICATING WITH YOUR COMPUTER ........................ 1-1 CHAPTER 2 HOW DATA IS STORED ..................................................... 2-1 Accessing Stored Data............................................................. 2-2 CHAPTER 3 HOW DATA IS PROCESSED ............................................... 3-1 The Basic Data Processing Cycle............................................. -

DISSERTATION High Performance Computing in Finance
Die approbierte Originalversion dieser Dissertation ist an der Hauptbibliothek der Technischen Universität Wien aufgestellt (http://www.ub.tuwien.ac.at). The approved original version of this thesis is available at the main library of the Vienna University of Technology (http://www.ub.tuwien.ac.at/englweb/). DISSERTATION High Performance Computing in Finance—On the Parallel Implementation of Pricing and Optimization Models ausgef¨uhrtzum Zwecke der Erlangung des akademischen Grades eines Doktors der technischen Wissenschaften unter der Leitung von o.Univ.-Prof. Dipl.-Ing. Mag. Dr. Gerti Kappel E188 Institut f¨urSoftwaretechnik und Interaktive Systeme eingereicht an der Technischen Universit¨atWien Fakult¨atf¨urInformatik von Dipl.-Ing. Hans Moritsch Smolagasse 4/2/8, A-1220 Wien Matr.Nr. 77 25 716 Wien, am 23. Mai 2006 Kurzfassung Der Einsatz von Hochleistungsrechnern in der Finanzwirtschaft ist sinnvoll bei der L¨osung von Anwendungsproblemen, die auf Szenarien und deren Eintrittswahrscheinlichkeiten definiert sind. Die Entwicklung von Aktienkursen und Zinsen kann auf diese Weise modelliert werden. Gehen diese Modelle von einem bekannten Zustand aus und erstrecken sie sich ¨uber mehrere Zeitperioden, so nehmen sie die Form von Szenario-B¨aumen an. Im Spezialfall “rekombinier- barer” B¨aume entstehen Gitterstrukturen. In dieser Arbeit werden zwei Problemklassen be- handelt, n¨amlich die Berechnung von Preisen f¨ur Finanzinstrumente, und die Optimierung von Anlageportefeuilles im Hinblick auf eine Zielfunktion mit Nebenbedingungen. Dynamische Optimierungsverfahren ber¨ucksichtigen mehrere Planungsperioden. Stochastische dynamische Verfahren beziehen Wahrscheinlichkeiten mit ein und f¨uhren daher zu (exponentiell wachsenden) Baumstrukturen, die sehr groß werden k¨onnen. Beispielsweise besitzt ein Baummodell dreier Anlagen ¨uber zehn Perioden, wobei die Preise durch Ausmaß und Wahrscheinlichkeit des Fall- ens bzw. -

Product Roadmap Presented by Roger Andrews on the Horizon…
Product Roadmap Presented by Roger Andrews On the horizon… Synergy/DE Version 11 New Version Aversion • Too many breaking changes • I need to re-test my entire application • I need to support my existing customers/version • I have to install new keys WE GET IT! So we’ve been avoiding it too! What Necessitated a Change in Version? Security • OpenSSL • Spectre / Meltdown Upgraded tooling for building Synergy • C runtime libraries • .NET Framework features • Visual Studio UCRT and Linux GCC compiler OS and hardware requirements Version 11: Security Why should I care? • You have to be secure from your client to your web server • You have to be secure from your website to your web server • You have to secure your data on disk • You have to secure the data before it gets to the disk • Anyone with FDIC/HIPAA/PCI compliance requirements MUST KEEP UP TO DATE!! Version 11: OpenSSL 1.1 • Openssl.org dropping security updates for 1.0.2 by Dec 2019 • Unix and VMS manufacturers continue to backport critical security fixes for a period of time, after OpenSSL drops support • All Windows customers using encryption of any kind should upgrade to Synergy/DE 11 and update OpenSSL to 1.1 to get continued security support • MANDATORY for FDIC / HIPAA / PCI compliance Version 11: OpenSSL 1.1 How do I get it? • SSL patches are as critical as OS patches • Windows: SSL patches must be manually applied • Unix: SSL patches come as part of OS patches…you must keep up to date • Some Unix distributions already ship with 1.1 by default (e.g., Fedora) • VMS: Support will -

SQL Replication
Introduction to SQL Replication The SQL Replication environment contains an example of how to implement the replication of a Synergy applications SDMS or RMS data to a SQL Server relational database in near-to-real-time. The techniques demonstrated in this example are based in large part on code that is automatically generated using CodeGen. It is therefore a requirement that the data structures and files that are to be replicated, including key definitions, are accurately described in a Synergy repository. Once the bulk of the code that is required to achieve the replication of data has been generated, the underlying application is modified by the addition of an I/O hooks object to any channels that are opened for update to files that are to be replicated. If your application already uses one or more subroutines to open its data files then those subroutines will be the only places that you need to alter, and the required change will typically be the addition of just a few lines of code to those routines. The code in the generated I/O hooks class detects and records changes to the ISAM and relative files that are being replicated. Once this change information is being recorded a single process called the "replicator" is used to cause those changes to be mirrored to corresponding tables in the relational database. There are several advantages to taking this kind of approach, some of the major ones being: • You don't need to re-design your Synergy applications to store the actual application data in an SQL database. -

2020 National IT & Engineering Compensation Survey
2020 National IT & Engineering Compensation Survey AAIM Employers' Association www.aaimea.org 314-968-3600 2020 National IT & Engineering Compensation Survey An Employer Associations of America (EAA) Sponsored Survey, coordinated by MRA – The Management Association in cooperation with employer associations nationwide. Published: September 2020 Next Publication: September 2021 Confidential Survey Report This survey is provided with the understanding that the information will: • remain strictly confidential • be restricted to authorized personnel only • not be used in collective bargaining or grievance proceedings • protect, completely, organizational identity National surveys produced by the EAA include: • National Business Trends Survey • National Executive Compensation Survey • National IT & Engineering Compensation Survey • National Policies & Benefits Survey • National Sales Compensation Survey • National Wage & Salary Survey © 2020 Employer Associations of America (EAA): All rights reserved. This survey is provided to the recipient to use as an internal compensation resource. Quotation from, or reproduction of, any part of the material contained in this survey, in any form or by any other means, without prior permission in writing from EAA or a survey co- sponsor named herein is prohibited. 2020 National IT & Engineering Compensation Survey Table of Contents Introduction Survey Information ............................................................................................................................................................................i -
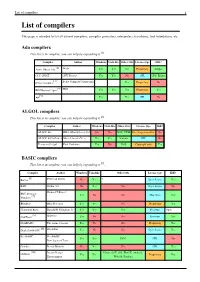
List of Compilers 1 List of Compilers
List of compilers 1 List of compilers This page is intended to list all current compilers, compiler generators, interpreters, translators, tool foundations, etc. Ada compilers This list is incomplete; you can help by expanding it [1]. Compiler Author Windows Unix-like Other OSs License type IDE? [2] Aonix Object Ada Atego Yes Yes Yes Proprietary Eclipse GCC GNAT GNU Project Yes Yes No GPL GPS, Eclipse [3] Irvine Compiler Irvine Compiler Corporation Yes Proprietary No [4] IBM Rational Apex IBM Yes Yes Yes Proprietary Yes [5] A# Yes Yes GPL No ALGOL compilers This list is incomplete; you can help by expanding it [1]. Compiler Author Windows Unix-like Other OSs License type IDE? ALGOL 60 RHA (Minisystems) Ltd No No DOS, CP/M Free for personal use No ALGOL 68G (Genie) Marcel van der Veer Yes Yes Various GPL No Persistent S-algol Paul Cockshott Yes No DOS Copyright only Yes BASIC compilers This list is incomplete; you can help by expanding it [1]. Compiler Author Windows Unix-like Other OSs License type IDE? [6] BaCon Peter van Eerten No Yes ? Open Source Yes BAIL Studio 403 No Yes No Open Source No BBC Basic for Richard T Russel [7] Yes No No Shareware Yes Windows BlitzMax Blitz Research Yes Yes No Proprietary Yes Chipmunk Basic Ronald H. Nicholson, Jr. Yes Yes Yes Freeware Open [8] CoolBasic Spywave Yes No No Freeware Yes DarkBASIC The Game Creators Yes No No Proprietary Yes [9] DoyleSoft BASIC DoyleSoft Yes No No Open Source Yes FreeBASIC FreeBASIC Yes Yes DOS GPL No Development Team Gambas Benoît Minisini No Yes No GPL Yes [10] Dream Design Linux, OSX, iOS, WinCE, Android, GLBasic Yes Yes Proprietary Yes Entertainment WebOS, Pandora List of compilers 2 [11] Just BASIC Shoptalk Systems Yes No No Freeware Yes [12] KBasic KBasic Software Yes Yes No Open source Yes Liberty BASIC Shoptalk Systems Yes No No Proprietary Yes [13] [14] Creative Maximite MMBasic Geoff Graham Yes No Maximite,PIC32 Commons EDIT [15] NBasic SylvaWare Yes No No Freeware No PowerBASIC PowerBASIC, Inc. -
Through the Years Licensing
Through the Years Technology Industry Synergex 1975 Microsoft is founded. S&H Computing announces the first 1976 version of TSX. DISC opens its doors as a DEC OEM, providing business systems to companies in the Sacramento area. 1978 DEC VAX is introduced. The first version of DBL (Data Business Language) is written by 11/780 Ken Lidster and Mike Morrissey in assembly language so they can create less expensive systems with DEC CPUs and third-party hardware. 1979 ISAM debuts in DBL version 1.2. 1980 Seagate Technology creates DBL version 2 is released. New the first hard disk drive for features include .INCLUDE, microcomputers. global storage definition, and fixed-length binary I/O. Denes labels in CONFIG.SYS as jump targets for CHAIN, DRSWITCH, GOTO, GOSUB and SWITCH directiv Denes labels in CONFIG.SYS as jump targets for CHAIN, DRSWITCH, GOTO, GOSUB and SWITCH directives. es.Denes labels in CONFIG.SYS as jump targets for CHAIN, DRSWITCH, GOTO, GOSUB and SWITC H directives. The IBM PC ships, introducing MS-DOS to the general public. 1983 The global internet is created, DISC opens a branch in and the first fully functional Sydney, Australia. “laptop” is introduced. 1984 Cellular phones become DBL is rewritten in C, commercially available. making version 4 truly cross-platform, running on VMS, TSX, and a range of MS-DOS and UNIX 1985 machines. Microsoft ships Windows 1.0. 1987 The first DBL Developer’s Conference is held. 1989 The World Wide Web is The first incarnations of invented, giving the world its Repository and ReportWriter first website. -

SQL Replication
Introduction The SQL Replication environment contains an example of how to implement the replication of a Synergy applications SDMS or RMS data to a SQL Server relational database in near-to-real-time. The techniques demonstrated in this example are based in large part on code that is automatically generated using CodeGen. It is therefore a requirement that the data structures and files that are to be replicated, including key definitions, are accurately described in a Synergy repository. Once the bulk of the code that is required to achieve the replication of data has been generated, the underlying application is modified by the addition of an I/O hooks object to any channels that are opened for update to files that are to be replicated. If your application already uses one or more subroutines to open its data files then those subroutines will be the only places that you need to alter, and the required change will typically be the addition of just a few lines of code to those routines. The code in the generated I/O hooks class detects and records changes to the ISAM and relative files that are being replicated. Once this change information is being recorded a single process called the "replicator" is used to cause those changes to be mirrored to corresponding tables in the relational database. There are several advantages to taking this kind of approach, some of the major ones being: • You don't need to re-design your Synergy applications to store the actual application data in an SQL database. To do this properly would be a very major re-write of any application. -

PIVT 02 Upoznavanje S Funkcijama, Sintaksom
Tema 02 Upoznavanje s funkcijama, sintaksom i semantikom softverskih alata dr Vladislav Miškovic [email protected] Fakultet za informatiku i računarstvo - Tehnički fakultet PRAKTIKUM - INTERNET I VEB TEHNOLOGIJE PRAKTIKUM - SISTEMI EPOSLOVANJA 2019/2020 Sadržaj 1. Uvod 2. Programski jezici za razvoj Veb aplikacija 3. Softverske platforme 4. Razvojni alati 5. Sistemi za upravljanje bazama podataka 6. Primer jednostavne transakcione ASP.NET aplikacije 1. Uvod 1. Osnovni pojmovi 2. Aplikativni okvir Microsoft .NET 1.1 Osnovni pojmovi • Veb sajt i jezik HTML • Veb dizajn Veb sajt i jezik HTML • Veb aplikacije su nastale nastale razvojem tehnologije izgradnje Veb sajtova – sajt je skup Veb stranica organizovanih u jedan ili više foldera na Veb serveru – relizuje se u jezicima koji podržava Veb čitač (HTML, CSS i JavaScript) • Jezik HTML se sastoji od oznaka (markup tags) • Aktuelna verzija je HTML 5 Veb dizajn • Dizajn je kreiranje nečega što ima namenu • Grafički dizajn Veb stranica obuhvata – Raspoređivanje elemenata (layout) – Tipografiju - izbor stilova teksta/fontove – Boje - izbor skupa boja za različite elemente – Grafiku - rasterske i vektorske slike, video – Navigaciju - menije i tastere Grafički dizajn stranice: raspored (layout) • Raspoređivanje elemenata 1. Principi umetničke kompozicije: prvo se obrati pažnja na centar i uglove 1) centar i uglovi 2. Podela vizuelnog polja: centar pažnje je na trećinama celine 2) mreža 3x3 3. Navike čitalaca zavise od kulture, npr. zapadna pisma se čitaju s leva prema dole 3) Gutenbergovo -

Synergy/DE Licensing Guide
Synergy/DE Licensing Guide This document describes Synergy/DE® products and how they are licensed. The policies and requirements described here may change for future products or future versions of existing Synergy/DE products. Any changes will be reflected in future updates to this Licensing Guide or a replacement document. Synergy/DE products are licensed for a specific platform. For a complete list of all supported platforms, see the Synergex website at www.synergex.com/supported-platforms. License Enforcement All Synergy/DE licenses are subject to the terms of the applicable Synergy/DE product license agreement executed by Synergex® and each “Licensee.” In most cases, the license enforcement built into Synergy/DE products will assist you in maintaining license compliance by enforcing the permitted number of users or connections. In all cases, however, you are responsible for using Synergy/DE products in accordance with the license terms and ensuring that your users do so as well. Product Descriptions Below are descriptions of the Synergy/DE products discussed in this document. For more detailed information, see the Synergex website at www.synergex.com/products. Synergy Runtime. Enables you to run Synergy applications using the regular runtime (dbr), one of the non-interactive runtimes (dbs, dbssvc, dbspriv), or the Synergy .NET runtime libraries. xfServer. Provides remote access to Synergy DBMS databases for Synergy applications. xfServerPlus. Enables you to execute remote applications built using xfServerPlus and xfNetLink. xfODBC. Provides access to Synergy DBMS databases from third-party ODBC-enabled applications. SQL Connection. An SQL API that enables Synergy applications to access third-party RDBMSs, such as Oracle®, MySQL™, and SQL Server®. -

Advancing Compilers
© 2014 IJIRT | Volume 1 Issue 6 | ISSN : 2349-6002 COMPILERS-STUDY FROM ZERO Vishal Sharma, Priyanka Yadav, Priti Yadav Computer Science Department, Dronacharya College of Engineering/ Maharishi Dayanand University, India Abstract- This paper gives the basic understanding of Compilers also aid in detecting programming errors compilers. The beginning of paper explain the term (which are all too common). compiler followed by its working, need and Compiler techniques also help to improve computer knowledge required in building compilers. Further security. we have explained the different types of compiler and For example, the Java Byte code Verifier helps to the application of compilers. The paper shows the study of different types of compilers.Thus, going guarantee that Java security rules are satisfied. through this paper one will end up with a good II. HOW DOES A COMPILER WORK? understanding of compilers and their future aspect. A compiler can be viewed in two parts: Index Terms- Analyser, Compilers, FORTRAN, LISP, UNIVAC. 1. Source Code Analyser: which takes as input I. INTRODUCTION source code as a sequence of characters, and Compilers are fundamental to modern computing. interprets it as a structure of symbols (vars, values, They act as translators, transforming human- operators, etc.) oriented programming languages into computer- oriented machine languages. 2. Object Code Generator: which takes the A compiler allows programmers to ignore the structural analysis from (1) and produces runnable machine-dependent details of programming. code as output? Compilers allow programs and programming skills to be machine-independent. Code Source analyser Code Code generator Object Code The Code Analyser typically has three stages: • Semantic Analyser: checks that variables are • Lexical Analysis: accepts the source code as a instantiated before use, etc.