How to Calibrate Your Adversary's Capabilities? Inverse Filtering for Counter-Autonomous Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![Arxiv:2104.00880V2 [Astro-Ph.HE] 6 Jul 2021](https://docslib.b-cdn.net/cover/4859/arxiv-2104-00880v2-astro-ph-he-6-jul-2021-94859.webp)
Arxiv:2104.00880V2 [Astro-Ph.HE] 6 Jul 2021
Draft version July 7, 2021 Typeset using LATEX twocolumn style in AASTeX63 Refined Mass and Geometric Measurements of the High-Mass PSR J0740+6620 E. Fonseca,1, 2, 3, 4 H. T. Cromartie,5, 6 T. T. Pennucci,7, 8 P. S. Ray,9 A. Yu. Kirichenko,10, 11 S. M. Ransom,7 P. B. Demorest,12 I. H. Stairs,13 Z. Arzoumanian,14 L. Guillemot,15, 16 A. Parthasarathy,17 M. Kerr,9 I. Cognard,15, 16 P. T. Baker,18 H. Blumer,3, 4 P. R. Brook,3, 4 M. DeCesar,19 T. Dolch,20, 21 F. A. Dong,13 E. C. Ferrara,22, 23, 24 W. Fiore,3, 4 N. Garver-Daniels,3, 4 D. C. Good,13 R. Jennings,25 M. L. Jones,26 V. M. Kaspi,1, 2 M. T. Lam,27, 28 D. R. Lorimer,3, 4 J. Luo,29 A. McEwen,26 J. W. McKee,29 M. A. McLaughlin,3, 4 N. McMann,30 B. W. Meyers,13 A. Naidu,31 C. Ng,32 D. J. Nice,33 N. Pol,30 H. A. Radovan,34 B. Shapiro-Albert,3, 4 C. M. Tan,1, 2 S. P. Tendulkar,35, 36 J. K. Swiggum,33 H. M. Wahl,3, 4 and W. W. Zhu37 1Department of Physics, McGill University, 3600 rue University, Montr´eal,QC H3A 2T8, Canada 2McGill Space Institute, McGill University, 3550 rue University, Montr´eal,QC H3A 2A7, Canada 3Department of Physics and Astronomy, West Virginia University, Morgantown, WV 26506-6315, USA 4Center for Gravitational Waves and Cosmology, Chestnut Ridge Research Building, Morgantown, WV 26505, USA 5Cornell Center for Astrophysics and Planetary Science and Department of Astronomy, Cornell University, Ithaca, NY 14853, USA 6NASA Hubble Fellowship Program Einstein Postdoctoral Fellow 7National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903, USA 8Institute of Physics, E¨otv¨osLor´anUniversity, P´azm´anyP. -

Beyond Traditional Assumptions in Fair Machine Learning
Beyond traditional assumptions in fair machine learning Niki Kilbertus Supervisor: Prof. Dr. Carl E. Rasmussen Advisor: Dr. Adrian Weller Department of Engineering University of Cambridge arXiv:2101.12476v1 [cs.LG] 29 Jan 2021 This thesis is submitted for the degree of Doctor of Philosophy Pembroke College October 2020 Acknowledgments The four years of my PhD have been filled with enriching and fun experiences. I owe all of them to interactions with exceptional people. Carl Rasmussen and Bernhard Schölkopf have put trust and confidence in me from day one. They enabled me to grow as a researcher and as a human being. They also taught me not to take things too seriously in moments of despair. Thank you! Adrian Weller’s contagious positive energy gave me enthusiasm and drive. He showed me how to be considerate and relentless at the same time. I thank him for his constant support and sharing his extensive network. Among others, he introduced me to Matt J. Kusner, Ricardo Silva, and Adrià Gascón who have been amazing role models and collaborators. I hope for many more joint projects with them! Moritz Hardt continues to be an inexhaustible source of inspiration and I want to thank him for his mentorship and guidance during my first paper. I was extremely fortunate to collaborate with outstanding people during my PhD beyond the ones already mentioned. I have learned a lot from every single one of them, thank you: Philip Ball, Stefan Bauer, Silvia Chiappa, Elliot Creager, Timothy Gebhard, Manuel Gomez Rodriguez, Anirudh Goyal, Krishna P. Gummadi, Ian Harry, Dominik Janzing, Francesco Locatello, Krikamol Muandet, Frederik Träuble, Isabel Valera, and Michael Veale. -

Egress Behavior from Select NYC COVID-19 Exposed Health Facilities March-May 2020 *Debra F. Laefer, C
Data Resource Profile: Egress Behavior from Select NYC COVID-19 Exposed Health Facilities March-May 2020 *Debra F. Laefer, Center for Urban Science and Progress and Department of Civil and Urban Engineering, New York University, 370 Jay St. #1303C, Brooklyn, NY 11201, USA, [email protected] Thomas Kirchner, School of Global Public Health, New York University Haoran (Frank) Jiang, Center for Data Science, New York University Darlene Cheong, Department of Biology, New York University Yunqi (Veronica) Jiang, Tandon School of Engineering, New York University Aseah Khan, Department of Biology, New York University Weiyi Qiu, Courant Institute of Mathematical Sciences, New York University Nikki Tai, Courant Institute of Mathematical Sciences, New York University Tiffany Truong, College of Arts and Science, New York University Maimunah Virk, College of Arts and Science, New York University Word count: 2845 1 Abstract Background: Vector control strategies are central to the mitigation and containment of COVID-19 and have come in the form of municipal ordinances that restrict the operational status of public and private spaces and associated services. Yet, little is known about specific population responses in terms of risk behaviors. Methods: To help understand the impact of those vector control variable strategies, a multi-week, multi- site observational study was undertaken outside of 19 New York City medical facilities during the peak of the city’s initial COVID-19 wave (03/22/20-05/19/20). The aim was to capture perishable data of the touch, destination choice, and PPE usage behavior of individuals egressing hospitals and urgent care centers. A major goal was to establish an empirical basis for future research on the way people interact with three- dimensional vector environments. -
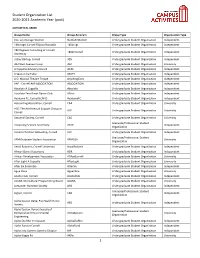
Student Organization List 2020-2021 Academic Year (Past)
Student Organization List 2020-2021 Academic Year (past) ALPHABETICAL ORDER Group Name Group Acronym Group Type Organization Type (not so) Average Women NotSoAvWomen Undergraduate Student Organization Independent 14Strings! Cornell Filipino Rondalla 14Strings Undergraduate Student Organization Independent 180 Degrees Consulting at Cornell 180dcCornell Undergraduate Student Organization Independent University 3 Day Startup, Cornell 3DS Undergraduate Student Organization Independent 302 Wait Avenue Co-op 302 Undergraduate Student Organization University A Cappella Advisory Council ACAC Undergraduate Student Organization Independent A Seat at the Table ASATT Undergraduate Student Organization Independent A.G. Musical Theatre Troupe AnythingGoes Undergraduate Student Organization Independent AAP - Cornell AAP ASSOCIATION ASSOCIATION Undergraduate Student Organization Independent Absolute A Cappella Absolute Undergraduate Student Organization Independent Absolute Zero Break Dance Club AZero Undergraduate Student Organization Independent Academy FC, Cornell (CAFC) AcademyFC Undergraduate Student Organization Independent Accounting Association, Cornell CAA Undergraduate Student Organization University ACE: The Ace/Asexual Support Group at ACE Undergraduate Student Organization University Cornell Actuarial Society, Cornell CAS Undergraduate Student Organization University Graduate/Professional Student Advancing Science And Policy ASAP Independent Organization Advent Christian Fellowship, Cornell ACF Undergraduate Student Organization Independent -

Scientometrics1
Scientometrics1 Loet Leydesdorff a and Staša Milojević b a Amsterdam School of Communication Research (ASCoR), University of Amsterdam, Kloveniersburgwal 48, 1012 CX Amsterdam, The Netherlands; [email protected] b School of Informatics and Computing, Indiana University, Bloomington 47405-1901, United States; [email protected]. Abstract The paper provides an overview of the field of scientometrics, that is: the study of science, technology, and innovation from a quantitative perspective. We cover major historical milestones in the development of this specialism from the 1960s to today and discuss its relationship with the sociology of scientific knowledge, the library and information sciences, and science policy issues such as indicator development. The disciplinary organization of scientometrics is analyzed both conceptually and empirically. A state-of-the-art review of five major research threads is provided. Keywords: scientometrics, bibliometrics, citation, indicator, impact, library, science policy, research management, sociology of science, science studies, mapping, visualization Cross References: Communication: Electronic Networks and Publications; History of Science; Libraries; Networks, Social; Merton, Robert K.; Peer Review and Quality Control; Science and Technology, Social Study of: Computers and Information Technology; Science and Technology Studies: Experts and Expertise; Social network algorithms and software; Statistical Models for Social Networks, Overview; 1 Forthcoming in: Micheal Lynch (Editor), International -

Hadronic Light-By-Light Contribution to $(G-2) \Mu $ from Lattice QCD: A
MITP/21-019 CERN-TH-2021-047 Hadronic light-by-light contribution to (g − 2)µ from lattice QCD: a complete calculation En-Hung Chao,1 Renwick J. Hudspith,1 Antoine G´erardin,2 Jeremy R. Green,3 Harvey B. Meyer,1, 4, 5 and Konstantin Ottnad1 1PRISMA+ Cluster of Excellence & Institut f¨urKernphysik, Johannes Gutenberg-Universit¨atMainz, D-55099 Mainz, Germany 2Aix Marseille Univ, Universit´ede Toulon, CNRS, CPT, Marseille, France 3Theoretical Physics Department, CERN, 1211 Geneva 23, Switzerland 4Helmholtz Institut Mainz, Staudingerweg 18, D-55128 Mainz, Germany 5GSI Helmholtzzentrum f¨urSchwerionenforschung, Darmstadt, Germany (Dated: April 7, 2021) We compute the hadronic light-by-light scattering contribution to the muon g 2 − from the up, down, and strange-quark sector directly using lattice QCD. Our calcu- lation features evaluations of all possible Wick-contractions of the relevant hadronic four-point function and incorporates several different pion masses, volumes, and lattice-spacings. We obtain a value of aHlbl = 106:8(14:7) 10−11 (adding statistical µ × and systematic errors in quadrature), which is consistent with current phenomenolog- ical estimates and a previous lattice determination. It now appears conclusive that the hadronic light-by-light contribution cannot explain the current tension between theory and experiment for the muon g 2. − I. INTRODUCTION The anomalous magnetic moment of the muon, aµ (g 2)µ=2, is one of the most precisely measured quantities of the Standard Model (SM)≡ of− particle physics. Its value is of considerable interest to the physics community as, currently, there exists a 3:7σ tension between the experimental determination of Ref. -
![Arxiv:2101.09252V2 [Math.DS] 9 Jun 2021 Eopsto,Salwwtrequation](https://docslib.b-cdn.net/cover/6269/arxiv-2101-09252v2-math-ds-9-jun-2021-eopsto-salwwtrequation-376269.webp)
Arxiv:2101.09252V2 [Math.DS] 9 Jun 2021 Eopsto,Salwwtrequation
Model and Data Reduction for Data Assimilation: Particle Filters Employing Projected Forecasts and Data with Application to a Shallow Water Model✩ Aishah Albarakatia,1, Marko Budiˇsi´ca,1, Rose Crockerb,1, Juniper Glass-Klaiberc,1, Sarah Iamsd,1, John Macleanb,1, Noah Marshalle,1, Colin Robertsf,1, Erik S. Van Vleckg,1 aDepartment of Mathematics, Clarkson University, Potsdam, NY 13699. bSchool of Mathematical Sciences, University of Adelaide, Adelaide SA 5005, Australia. cDepartment of Physics, Mount Holyoke College, South Hadley, MA 01075. dPaulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138. eDepartment of Mathematics and Statistics, McGill University, Montreal, Quebec H3A 0B9, Canada. fDepartment of Mathematics, Colorado State University, Ft. Collins, CO 80523. gDepartment of Mathematics, University of Kansas, Lawrence, KS 66045. Abstract The understanding of nonlinear, high dimensional flows, e.g, atmospheric and ocean flows, is critical to address the impacts of global climate change. Data Assimilation (DA) techniques combine physical models and observa- tional data, often in a Bayesian framework, to predict the future state of the model and the uncertainty in this prediction. Inherent in these systems are noise (Gaussian and non-Gaussian), nonlinearity, and high dimensional- ity that pose challenges to making accurate predictions. To address these issues we investigate the use of both model and data dimension reduction based on techniques including Assimilation in the Unstable Subspace (AUS), Proper Orthogonal Decomposition (POD), and Dynamic Mode Decomposition (DMD). Algorithms to take advantage of projected physical and data models may be combined with DA techniques such as Ensemble Kalman Filter (EnKF) and Particle Filter (PF) variants. -

Dice: Deep Significance Clustering
DICE: DEEP SIGNIFICANCE CLUSTERING FOR OUTCOME-AWARE STRATIFICATION Yufang Huang Kelly M. Axsom John Lee Cornell University Columbia University Irving Medical Center Weill Cornell Medicine [email protected] [email protected] [email protected] Lakshminarayanan Subramanian Yiye Zhang New York University Cornell University [email protected] [email protected] January 8, 2021 ABSTRACT We present deep significance clustering (DICE), a framework for jointly performing representation learning and clustering for “outcome-aware” stratification. DICE is intended to generate cluster membership that may be used to categorize a population by individual risk level for a targeted outcome. Following the representation learning and clustering steps, we embed the objective function in DICE with a constraint which requires a statistically significant association between the outcome and cluster membership of learned representations. DICE further includes a neural architecture search step to maximize both the likelihood of representation learning and outcome classification accuracy with cluster membership as the predictor. To demonstrate its utility in medicine for patient risk-stratification, the performance of DICE was evaluated using two datasets with different outcome ratios extracted from real-world electronic health records. Outcomes are defined as acute kidney injury (30.4%) among a cohort of COVID-19 patients, and discharge disposition (36.8%) among a cohort of heart failure patients, respectively. Extensive results demonstrate that -

Arxiv.Org | Cornell University Library, July, 2019. 1
arXiv.org | Cornell University Library, July, 2019. Extremophiles: a special or general case in the search for extra-terrestrial life? Ian von Hegner Aarhus University Abstract Since time immemorial life has been viewed as fragile, yet over the past few decades it has been found that many extreme environments are inhabited by organisms known as extremophiles. Knowledge of their emergence, adaptability, and limitations seems to provide a guideline for the search of extra-terrestrial life, since some extremophiles presumably can survive in extreme environments such as Mars, Europa, and Enceladus. Due to physico-chemical constraints, the first life necessarily came into existence at the lower limit of it‟s conceivable complexity. Thus, the first life could not have been an extremophile, furthermore, since biological evolution occurs over time, then the dual knowledge regarding what specific extremophiles are capable of, and to the analogue environment on extreme worlds, will not be sufficient as a search criterion. This is because, even though an extremophile can live in an extreme environment here-and-now, its ancestor however could not live in that very same environment in the past, which means that no contemporary extremophiles exist in that environment. Furthermore, a theoretical framework should be able to predict whether extremophiles can be considered a special or general case in the galaxy. Thus, a question is raised: does Earth‟s continuous habitability represent an extreme or average value for planets? Thus, dependent on whether it is difficult or easy for worlds to maintain the habitability, the search for extra- terrestrial life with a focus on extremophiles will either represent a search for dying worlds, or a search for special life on living worlds, focusing too narrowly on extreme values. -

Pronounced Non-Markovian Features in Multiply-Excited, Multiple-Emitter Waveguide-QED: Retardation-Induced Anomalous Population Trapping
Pronounced non-Markovian features in multiply-excited, multiple-emitter waveguide-QED: Retardation-induced anomalous population trapping Alexander Carmele,1 Nikolett Nemet,1, 2 Victor Canela,1, 2 and Scott Parkins1, 2 1Department of Physics, University of Auckland, Private Bag 92019, Auckland, New Zealand 2Dodd-Walls Centre for Photonic and Quantum Technologies, New Zealand (Dated: February 5, 2020) The Markovian approximation is widely applied in the field of quantum optics due to the weak frequency dependence of the vacuum field amplitude, and in consequence non-Markovian effects are typically regarded to play a minor role in the optical electron-photon interaction. Here, we give an example where non-Markovianity changes the qualitative behavior of a quantum optical system, rendering the Markovian approximation quantitatively and qualitatively insufficient. Namely, we study a multiple-emitter, multiple-excitation waveguide quantum-electrodynamic (waveguide-QED) system and include propagation time delay. In particular, we demonstrate anomalous population trapping as a result of the retardation in the excitation exchange between the waveguide and three initially excited emitters. Allowing for local phases in the emitter-waveguide coupling, this pop- ulation trapping cannot be recovered using a Markovian treatment, proving the essential role of non-Markovian dynamics in the process. Furthermore, this time-delayed excitation exchange allows for a novel steady state, in which one emitter decays entirely to its ground state while the other two -

Standpoints on Psychiatric Deinstitutionalization Alix Rule Submitted in Partial Fulfillment of the Requirements for the Degre
Standpoints on Psychiatric Deinstitutionalization Alix Rule Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2018 © 2018 Alix Rule All rights reserved ABSTRACT Standpoints on Psychiatric Deinstitutionalization Alix Rule Between 1955 and 1985 the United States reduced the population confined in its public mental hospitals from around 600,000 to less than 110,000. This dissertation provides a novel analysis of the movement that advocated for psychiatric deinstitutionalization. To do so, it reconstructs the unfolding setting of the movement’s activity historically, at a number of levels: namely, (1) the growth of private markets in the care of mental illness and the role of federal welfare policy; (2) the contested role of states as actors in driving the process by which these developments effected changes in the mental health system; and (3) the context of relevant events visible to contemporaries. Methods of computational text analysis help to reconstruct this social context, and thus to identify the closure of key opportunities for movement action. In so doing, the dissertation introduces an original method for compiling textual corpora, based on a word-embedding model of ledes published by The New York Times from 1945 to the present. The approach enables researchers to achieve distinct, but equally consistent, actor-oriented descriptions of the social world spanning long periods of time, the forms of which are illustrated here. Substantively, I find that by the early 1970s, the mental health system had disappeared from public view as a part of the field of general medicine — and with it a target around which the existing movement on behalf of the mentally ill might have effectively reorganized itself. -

Employee Wellbeing at Cornell Re
Your guide to resources that support all the dimensions of your wellbeing. HR.CORNELL.EDU/WELLBEING 1 2 1.6.20 Dear Colleague, During your time with Cornell, we want you to be well and THRIVE. Cornell invests in benefits, programs, and services to support employee wellbeing. This guide features a wide range of university (and many community!) resources available to support you in various dimensions of your wellbeing. As you browse this guide, which is organized around Cornell’s Seven Dimensions of Wellbeing model pictured below, you’ll find many resources cross-referenced in multiple dimensions. This illustrates the multifaceted nature of wellbeing. It is often non-linear in nature, and our most important elements shift as our work and Mary Opperman personal lives evolve. CHRO and Vice President Division of Human Resources We experience wellbeing both personally and as members of our various communities, including our work community. We each have opportunities to positively contribute to Cornell’s culture of wellbeing as we celebrate our colleagues’ life events, support one another during difficult times, share resources, and find creative approaches to how, where, and when work gets done. Behind this page is a “quick start directory” of Cornell wellbeing-related contacts. Please save this page and reach out any time you need assistance! Although some of these resources are specific to Cornell’s Ithaca campus, we recognize and are continuing to focus on expanding offerings to our employees in all locations. Thank you for all of your contributions