DOCSLIB.ORG

Appendix a Linear Algebra

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Appendix a Linear Algebra Appendix A Linear Algebra This appendix surveys some of the important basic concepts in linear algebra that often appear in computer graphics literature. It is not meant to be a complete reference for linear algebra; however, it covers the concepts required to read this book. Skilled readers may skip this appendix. A.1 Matrices A matrix is an array of numbers, entries, components, terms or elements. An n × m matrix A consists of n rows and m columns and is expressed as ⎡ ⎤ a11 a12 ... a1m ⎢ ⎥ ⎢ a21 a22 ... a2m ⎥ A = ⎢ . ⎥ . (A.1) ⎣ . .. ⎦ an1 an2 ... anm A matrix is called square if the number of rows and the number of columns are equal (i.e., if n = m); otherwise, it is called rectangular (i.e., if n = m). A square matrix is orthogonal when the dot product (Sect. A.4.3.2)ofanypair of rows or any pair of columns is zero and when the columns and the rows are unit vectors (Sect. A.4.1). Also, the inverse (Sect. A.2.2) and the transpose (Sect. A.2.3) of an orthogonal matrix are equal. A.1.1 Identity Matrix An identity matrix I is a square matrix where aij = 1 when i = j and aij = 0 otherwise. Hence, an identity matrix is expressed as R. Elias, Digital Media, DOI: 10.1007/978-3-319-05137-6, 625 © Springer International Publishing Switzerland 2014 626 Appendix A: Linear Algebra ⎡ ⎤ 10... 0 ⎢ ⎥ ⎢ 01... 0 ⎥ I = ⎢ . ⎥ . (A.2) ⎣ . .. ⎦ 00... 1 As a convention, the identity matrix is always referred to by the letter I. A.1.2 Diagonal Matrix A diagonal matrix D is a square matrix with zero entries except for those of the main diagonal (i.e., where i = j). In other words, an n × n matrix D is diagonal if aij = 0 | i = j ∀ i, j ∈{1, 2,...,n}. Hence, a diagonal matrix is expressed as ⎡ ⎤ a11 0 ... 0 ⎢ ⎥ ⎢ 0 a22 ... 0 ⎥ D = ⎢ . ⎥ . (A.3) ⎣ . .. ⎦ 00... ann The same diagonal matrix may also be denoted as D = diag(a11, a22,...,ann) where a11, a22,...,ann are the elements of the main diagonal. Matrix diagonalization is converting a square matrix into a diagonal matrix. A.1.3 Symmetric Matrix A symmetric matrix is a square matrix where aij = a ji. For an n × n, it can be expressed as ⎡ ⎤ a11 a12 ... a1n ⎢ ⎥ ⎢ a12 a22 ... a2n ⎥ A = ⎢ . ⎥ . (A.4) ⎣ . .. ⎦ a1n a2n ... ann In this case, A = AT . This implies that A−1AT = I. A.1.4 Anti-Symmetric Matrix An anti-symmetric or skew symmetric matrix is a square matrix where aij =−a ji. For an n × n, it can be expressed as Appendix A: Linear Algebra 627 ⎡ ⎤ 0 a12 ... a1n ⎢ ⎥ ⎢ −a12 0 ... a2n ⎥ A = ⎢ . ⎥ . (A.5) ⎣ . .. ⎦ −a1n −a2n ... 0 An anti-symmetric matrix must have zeros on its diagonal. In this case, A =−AT . This implies that −A−1AT = I. A.2 Matrix Operations Some matrix operations are applied to single matrices (e.g., determinant, inverse, transpose and scalar multiplication) while others are applied to pairs of matrices (e.g., addition, subtraction and multiplication). In the following sections, we will talk about some of the most important matrix operations. A.2.1 Matrix Determinant A matrix determinant is defined for a square matrix. A 2× 2 matrix determinant |A| is defined as a11 a12 a11 a12 |A|≡det ≡ a21 a22 a21 a22 (A.6) = a11a22 − a12a21. A3× 3 matrix determinant |A| is defined as ⎡ ⎤ a11 a12 a13 a11 a12 a13 ⎣ ⎦ |A|≡det a21 a22 a23 ≡ a21 a22 a23 a31 a32 a33 a31 a32 a33 a22 a23 a21 a23 a21 a22 = a11 − a12 + a13 a32 a33 a31 a33 a31 a32 = a11(a22a33 − a23a32) − a12(a21a33 − a23a31) + a13(a21a32 − a22a31). (A.7) A.2.2 Matrix Inverse − − The inverse of a square matrix A is another square matrix A 1 such that AA 1 = I. a a If A = 11 12 then the inverse A−1 is calculated as a21 a22 628 Appendix A: Linear Algebra − −1 = 1 a22 a12 A |A| −a21 a11 − (A.8) = 1 a22 a12 . a a − a a 11 22 12 21 −a21 a11 For a 3 × 3matrixA,theinverseA−1 is defined as ⎡ ⎤ a22 a23 a13 a12 a12 a13 ⎢ ⎥ ⎢ a32 a33 a33 a32 a22 a23 ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − 1 ⎢ a23 a21 a11 a13 a13 a11 ⎥ A 1 = ⎢ ⎥ . (A.9) |A| ⎢ a33 a31 a31 a33 a23 a21 ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ a21 a22 a12 a11 a11 a12 a31 a32 a32 a31 a21 a22 Example A.1 [Matrices–inverse] Compute the inverse for the following matrix: ⎡ ⎤ 111 A = ⎣ 331⎦ . 411 Solution A.1 There are two steps: 1. Get the determinant |A| by applying Eq. (A.7). Thus, |A|=1 × (3 × 1 − 1 × 1) − 1 × (3 × 1 − 4 × 1) + 1 × (3 × 1 − 3 × 4) =−6. 2. Get the inverse A−1 by applying Eq. (A.9)as ⎡ ⎤ 31 11 11 ⎢ ⎥ ⎢ 11 11 31 ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − 1 ⎢ 13 11 11 ⎥ A 1 = ⎢ ⎥ −6 ⎢ 14 41 13 ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 33 11 11 41 14 33 ⎡ ⎤ 20−2 1 = ⎣ 1 −32⎦ − 6 −93 0 Appendix A: Linear Algebra 629 ⎡ ⎤ − 1 0 1 ⎢ 3 3 ⎥ = ⎢ − 1 1 − 1 ⎥ . ⎣ 6 2 3 ⎦ 1 − 1 1 2 2 0 A.2.3 Matrix Transpose The transpose of a matrix A is the matrix obtained by replacing all elements aij with a ji (i.e., columns become rows and rows become columns). The transpose of A is denoted by AT . Thus, we can write (AT )T = A. Example A.2 [Matrices–transpose] 123 Get the transpose of A where A = . 456 Solution A.2 The inverse can be expressed as ⎡ ⎤ T 14 123 AT = = ⎣ 25⎦ . 456 36 A.2.4 Addition and Subtraction Matrices of the same size can be added together (or subtracted from each other) by adding (or subtracting) the corresponding elements. Thus, for two matrices A and B of size n × m, we may have ⎡ ⎤ ⎡ ⎤ a11 a12 ... a1m b11 b12 ... b1m ⎢ ⎥ ⎢ ⎥ ⎢ a21 a22 ... a2m ⎥ ⎢ b21 b22 ... b2m ⎥ A + B = ⎢ . ⎥ + ⎢ . ⎥ ⎣ . .. ⎦ ⎣ . .. ⎦ an1 an2 ... anm bn1 bn2 ... bnm ⎡ ⎤ (A.10) a11 + b11 a12 + b12 ... a1m + b1m ⎢ ⎥ ⎢ a21 + b21 a22 + b22 ... a2m + b2m ⎥ = ⎢ . ⎥ ⎣ . .. ⎦ an1 + bn1 an2 + bn2 ... anm + bnm or 630 Appendix A: Linear Algebra ⎡ ⎤ ⎡ ⎤ a11 a12 ... a1m b11 b12 ... b1m ⎢ ⎥ ⎢ ⎥ ⎢ a21 a22 ... a2m ⎥ ⎢ b21 b22 ... b2m ⎥ A − B = ⎢ . ⎥ − ⎢ . ⎥ ⎣ . .. ⎦ ⎣ . .. ⎦ an1 an2 ... anm bn1 bn2 ... bnm ⎡ ⎤ (A.11) a11 − b11 a12 − b12 ... a1m − b1m ⎢ ⎥ ⎢ a21 − b21 a22 − b22 ... a2m − b2m ⎥ = ⎢ . ⎥ . ⎣ . .. ⎦ an1 − bn1 an2 − bn2 ... anm − bnm Example A.3 [Matrices–addition and subtraction ] 1234 355 6 Consider two matrices A and B where A = and B = . 5677 78910 Calculate the addition A+B and the subtractions A−B and B−A. Solution A.3 The addition is performed by adding corresponding terms as 1234 355 6 A + B = + 5677 78910 + + + + = 1 32 53 54 6 5 + 76+ 87+ 97+ 10 = 47810. 12 14 16 17 The subtraction is performed by subtracting corresponding terms as 1234 355 6 A − B = − 5677 78910 − − − − = 1 32 53 54 6 5 − 76− 87− 97− 10 − − − − = 2 3 2 2 −2 −2 −2 −3 355 6 1234 B − A = − 78910 5677 − − − − = 3 15 25 36 4 7 − 58− 69− 710− 7 = 2322 . 2223 Notice that B − A =−[A − B]. Appendix A: Linear Algebra 631 Example A.4 [Matrices–addition and subtraction ] 123 35 Consider two matrices A and B where A = and B = . Calculate 567 78 the addition A+B and the subtractions A−B and B−A. Solution A.4 Since the sizes of the matrices are different, none of the operations can be performed. A.2.5 Scalar Multiplication Scalar multiplication is an operation performed by multiplying each of the elements of a matrix by a scalar value. Thus, for a n × m matrix A and a scalar value s,we can write ⎡ ⎤ ⎡ ⎤ a11 a12 ... a1m sa11 sa12 ... sa1m ⎢ ⎥ ⎢ ⎥ ⎢ a21 a22 ... a2m ⎥ ⎢ sa21 sa22 ... sa2m ⎥ sA = s ⎢ . ⎥ = ⎢ . ⎥ . (A.12) ⎣ . .. ⎦ ⎣ . .. ⎦ an1 an2 ... anm san1 san2 ... sanm Example A.5 [Matrices–scalar multiplication ] 123 If a matrix A is defined as A = , get the result of sA where s = 2.5. 456 Solution A.5 The scalar value is multiplied by each matrix term individually. Thus, 123 2.557.5 sA = 2.5 = . 456 10 12.515 Example A.6 [Matrices–scalar multiplication and addition/subtraction ] 1234 355 6 Consider two matrices A and B where A = and B = . 5677 78910 Calculate A+2B and 2A−B. Solution A.6 1234 355 6 A + 2B = + 2 5677 78910 = 1234 + 6101012 5677 14 16 18 20 + + + + = 1 62 10 3 10 4 12 5 + 14 6 + 16 7 + 18 7 + 20 = 7121316 . 19 22 25 27 632 Appendix A: Linear Algebra 1234 355 6 2A − B = 2 − 5677 78910 = 2468 − 355 6 10 12 14 14 78910 − − − − = 2 34 56 58 6 10 − 712− 814− 914− 10 − − = 1 112 . 3454 A.2.6 Matrix Multiplication In order to multiply two matrices A and B, the number of columns of the first matrix A must be equal to the number of rows of the second B. The resulting matrix has the same number of rows as the first and the same number of columns as the second. Thus, if A is of size n × m and B is of size m × k, the resulting matrix C will be of size n × k. This can be written as AB = ⎡C ⎤ c11 c12 ... c1k ⎢ ⎥ ⎢ c21 c22 ... c2k ⎥ = ⎢ . ⎥ ⎣ . .. ⎦ cn1 cn2 ... cnk ⎡ ⎤ i< =m i< =m i< =m ⎢ a i bi a i bi ... a i bik ⎥ (A.13) ⎢ 1 1 1 2 1 ⎥ ⎢ i=1 i=1 i=1 ⎥ ⎢ i< =m i< =m i< =m ⎥ ⎢ ... ⎥ ⎢ a2i bi1 a2i bi2 a2i bik ⎥ = ⎢ i=1 i=1 i=1 ⎥ , ⎢ . ⎥ ⎢ . .. ⎥ ⎢ ⎥ ⎣ i< =m i< =m i< =m ⎦ anibi1 anibi2 ..
Load more

Recommended publications
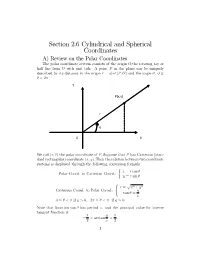
  • Section 2.6 Cylindrical and Spherical Coordinates
    Section 2.6 Cylindrical and Spherical Coordinates A) Review on the Polar Coordinates The polar coordinate system consists of the origin O,the rotating ray or half line from O with unit tick. A point P in the plane can be uniquely described by its distance to the origin r = dist (P, O) and the angle µ, 0 µ < 2¼ : · Y P(x,y) r θ O X We call (r, µ) the polar coordinate of P. Suppose that P has Cartesian (stan- dard rectangular) coordinate (x, y) .Then the relation between two coordinate systems is displayed through the following conversion formula: x = r cos µ Polar Coord. to Cartesian Coord.: y = r sin µ ½ r = x2 + y2 Cartesian Coord. to Polar Coord.: y tan µ = ( p x 0 µ < ¼ if y > 0, 2¼ µ < ¼ if y 0. · · · Note that function tan µ has period ¼, and the principal value for inverse tangent function is ¼ y ¼ < arctan < . ¡ 2 x 2 1 So the angle should be determined by y arctan , if x > 0 xy 8 arctan + ¼, if x < 0 µ = > ¼ x > > , if x = 0, y > 0 < 2 ¼ , if x = 0, y < 0 > ¡ 2 > > Example 6.1. Fin:>d (a) Cartesian Coord. of P whose Polar Coord. is ¼ 2, , and (b) Polar Coord. of Q whose Cartesian Coord. is ( 1, 1) . 3 ¡ ¡ ³ So´l. (a) ¼ x = 2 cos = 1, 3 ¼ y = 2 sin = p3. 3 (b) r = p1 + 1 = p2 1 ¼ ¼ 5¼ tan µ = ¡ = 1 = µ = or µ = + ¼ = . 1 ) 4 4 4 ¡ 5¼ Since ( 1, 1) is in the third quadrant, we choose µ = so ¡ ¡ 4 5¼ p2, is Polar Coord.
    [Show full text]
  • Designing Patterns with Polar Equations Using Maple
    Designing Patterns with Polar Equations using Maple Somasundaram Velummylum Claflin University Department of Mathematics and Computer Science 400 Magnolia St Orangeburg, South Carolina 29115 U.S.A [email protected] The Cartesian coordinates and polar coordinates can be used to identify a point in two dimensions. The polar coordinate system has a fixed point O called the origin or pole and a directed half –line called the polar axis with end point O. A point P on the plane can be described by the polar coordinates ( r, θ ), where r is the radial distance from the origin and θ is the angle made by OP with the polar axis. Several important types of graphs have equations that are simpler in polar form than in rectangular form. For example, the polar equation of a circle having radius a and centered at the origin is simply r = a. In other words , polar coordinate system is useful in describing two dimensional regions that may be difficult to describe using Cartesian coordinates. For example, graphing the circle x 2 + y 2 = a 2 in Cartesian coordinates requires two functions, one for the upper half and one for the lower half. In polar coordinate system, the same circle has the very simple representation r = a. Maple can be used to create patterns in two dimensions using polar coordinate system. When we try to analyze two dimensional patterns mathematically it will be helpful if we can draw a set of patterns in different colors using the help of technology. To investigate and compare some patterns we will go through some examples of cardioids and rose curves that are drawn using Maple.
    [Show full text]
  • Learning Geometric Algebra by Modeling Motions of the Earth and Shadows of Gnomons to Predict Solar Azimuths and Altitudes
    Learning Geometric Algebra by Modeling Motions of the Earth and Shadows of Gnomons to Predict Solar Azimuths and Altitudes April 24, 2018 James Smith [email protected] https://mx.linkedin.com/in/james-smith-1b195047 \Our first step in developing an expression for the orientation of \our" gnomon: Diagramming its location at the instant of the 2016 December solstice." Abstract Because the shortage of worked-out examples at introductory levels is an obstacle to widespread adoption of Geometric Algebra (GA), we use GA to calculate Solar azimuths and altitudes as a function of time via the heliocentric model. We begin by representing the Earth's motions in GA terms. Our representation incorporates an estimate of the time at which the Earth would have reached perihelion in 2017 if not affected by the Moon's gravity. Using the geometry of the December 2016 solstice as a starting 1 point, we then employ GA's capacities for handling rotations to determine the orientation of a gnomon at any given latitude and longitude during the period between the December solstices of 2016 and 2017. Subsequently, we derive equations for two angles: that between the Sun's rays and the gnomon's shaft, and that between the gnomon's shadow and the direction \north" as traced on the ground at the gnomon's location. To validate our equations, we convert those angles to Solar azimuths and altitudes for comparison with simulations made by the program Stellarium. As further validation, we analyze our equations algebraically to predict (for example) the precise timings and locations of sunrises, sunsets, and Solar zeniths on the solstices and equinoxes.
    [Show full text]
  • Schaum's Outline of Linear Algebra (4Th Edition)
    SCHAUM’S SCHAUM’S outlines outlines Linear Algebra Fourth Edition Seymour Lipschutz, Ph.D. Temple University Marc Lars Lipson, Ph.D. University of Virginia Schaum’s Outline Series New York Chicago San Francisco Lisbon London Madrid Mexico City Milan New Delhi San Juan Seoul Singapore Sydney Toronto Copyright © 2009, 2001, 1991, 1968 by The McGraw-Hill Companies, Inc. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior writ- ten permission of the publisher. ISBN: 978-0-07-154353-8 MHID: 0-07-154353-8 The material in this eBook also appears in the print version of this title: ISBN: 978-0-07-154352-1, MHID: 0-07-154352-X. All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark. Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in corporate training programs. To contact a representative please e-mail us at [email protected]. TERMS OF USE This is a copyrighted work and The McGraw-Hill Companies, Inc. (“McGraw-Hill”) and its licensors reserve all rights in and to the work.
    [Show full text]
  • Polar Coordinates and Calculus.Wxp
    Polar Coordinates and Calculus Recall that in the Polar coordinate system the coordinates ) represent <ß the directed distance from the pole to the point and the directed angle, counterclockwise from the polar axis to the segment from the pole to the point. A polar function would be of the form: ) . < œ 0 To find the slope of the tangent line of a polar graph we will parameterize the equation. ) ( Assume is a differentiable function of ) ) <œ0 0 ¾Bœ<cos))) œ0 cos and Cœ< sin ))) œ0 sin . .C .C .) Recall also that œ .B .B .) 1Þ Find the derivative of < œ # sin ) Remember that horizontal tangent lines occur when and that vertical tangent lines occur when page 1 2 Find the HTL and VTL for cos ) and sketch the graph. Þ < œ # " page 2 Recall our formula for the derivative of a function in polar coordinates. Since Bœ<cos))) œ0 cos and Cœ< sin ))) œ0 sin , we can conclude .C .C .) that œ.B œ .B .) Solutions obtained by setting < œ ! gives equations of tangent lines through the pole. 3Þ Find the equations of the tangent line(s) through the pole if <œ#sin #Þ) page 3 To find the arc length of a polar curve, you have two options. 1) You can use the parametrization of the polar curve: cos))) cos and sin ))) sin Bœ< œ0 Cœ< œ0 then use the arc length formula for parametric curves: " w # w # 'α ÈÐBÐ) ÑÑ ÐCÐ ) ÑÑ . ) or, 2) You can use an alternative formula for arc length in polar form: " <# Ð.< Ñ # .
    [Show full text]
  • Exercise 7.5
    IN SUMMARY Key Idea • A projection of one vector onto another can be either a scalar or a vector. The difference is the vector projection has a direction. A A a a u u O O b NB b N B Scalar projection of a on b Vector projection of a on b Need to Know ! ! ! ! a # b ! • The scalar projection of a on b ϭϭ! 0 a 0 cos u, where u is the angle @ b @ ! ! between a and b. ! ! ! ! ! ! a # b ! a # b ! • The vector projection of a on b ϭ ! b ϭ a ! ! b b @ b @ 2 b # b ! • The direction cosines for OP ϭ 1a, b, c2 are a b cos a ϭ , cos b ϭ , 2 2 2 2 2 2 Va ϩ b ϩ c Va ϩ b ϩ c c cos g ϭ , where a, b, and g are the direction angles 2 2 2 Va ϩ b ϩ c ! between the position vector OP and the positive x-axis, y-axis and z-axis, respectively. Exercise 7.5 PART A ! 1. a. The vector a ϭ 12, 32 is projected onto the x-axis. What is the scalar projection? What is the vector projection? ! b. What are the scalar and vector projections when a is projected onto the y-axis? 2. Explain why it is not possible to obtain! either a scalar! projection or a vector projection when a nonzero vector x is projected on 0. 398 7.5 SCALAR AND VECTOR PROJECTIONS NEL ! ! 3. Consider two nonzero vectors,a and b, that are perpendicular! ! to each other.! Explain why the scalar and vector projections of a on b must! be !0 and 0, respectively.
    [Show full text]
  • MATH 304 Linear Algebra Lecture 24: Scalar Product. Vectors: Geometric Approach
    MATH 304 Linear Algebra Lecture 24: Scalar product. Vectors: geometric approach B A B′ A′ A vector is represented by a directed segment. • Directed segment is drawn as an arrow. • Different arrows represent the same vector if • they are of the same length and direction. Vectors: geometric approach v B A v B′ A′ −→AB denotes the vector represented by the arrow with tip at B and tail at A. −→AA is called the zero vector and denoted 0. Vectors: geometric approach v B − A v B′ A′ If v = −→AB then −→BA is called the negative vector of v and denoted v. − Vector addition Given vectors a and b, their sum a + b is defined by the rule −→AB + −→BC = −→AC. That is, choose points A, B, C so that −→AB = a and −→BC = b. Then a + b = −→AC. B b a C a b + B′ b A a C ′ a + b A′ The difference of the two vectors is defined as a b = a + ( b). − − b a b − a Properties of vector addition: a + b = b + a (commutative law) (a + b) + c = a + (b + c) (associative law) a + 0 = 0 + a = a a + ( a) = ( a) + a = 0 − − Let −→AB = a. Then a + 0 = −→AB + −→BB = −→AB = a, a + ( a) = −→AB + −→BA = −→AA = 0. − Let −→AB = a, −→BC = b, and −→CD = c. Then (a + b) + c = (−→AB + −→BC) + −→CD = −→AC + −→CD = −→AD, a + (b + c) = −→AB + (−→BC + −→CD) = −→AB + −→BD = −→AD. Parallelogram rule Let −→AB = a, −→BC = b, −−→AB′ = b, and −−→B′C ′ = a. Then a + b = −→AC, b + a = −−→AC ′.
    [Show full text]
  • Linear Algebra - Part II Projection, Eigendecomposition, SVD
    Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Punit Shah's slides) 2019 Linear Algebra, Part II 2019 1 / 22 Brief Review from Part 1 Matrix Multiplication is a linear tranformation. Symmetric Matrix: A = AT Orthogonal Matrix: AT A = AAT = I and A−1 = AT L2 Norm: s X 2 jjxjj2 = xi i Linear Algebra, Part II 2019 2 / 22 Angle Between Vectors Dot product of two vectors can be written in terms of their L2 norms and the angle θ between them. T a b = jjajj2jjbjj2 cos(θ) Linear Algebra, Part II 2019 3 / 22 Cosine Similarity Cosine between two vectors is a measure of their similarity: a · b cos(θ) = jjajj jjbjj Orthogonal Vectors: Two vectors a and b are orthogonal to each other if a · b = 0. Linear Algebra, Part II 2019 4 / 22 Vector Projection ^ b Given two vectors a and b, let b = jjbjj be the unit vector in the direction of b. ^ Then a1 = a1 · b is the orthogonal projection of a onto a straight line parallel to b, where b a = jjajj cos(θ) = a · b^ = a · 1 jjbjj Image taken from wikipedia. Linear Algebra, Part II 2019 5 / 22 Diagonal Matrix Diagonal matrix has mostly zeros with non-zero entries only in the diagonal, e.g. identity matrix. A square diagonal matrix with diagonal elements given by entries of vector v is denoted: diag(v) Multiplying vector x by a diagonal matrix is efficient: diag(v)x = v x is the entrywise product. Inverting a square diagonal matrix is efficient: 1 1 diag(v)−1 = diag [ ;:::; ]T v1 vn Linear Algebra, Part II 2019 6 / 22 Determinant Determinant of a square matrix is a mapping to a scalar.
    [Show full text]
  • Basics of Linear Algebra
    Basics of Linear Algebra Jos and Sophia Vectors ● Linear Algebra Definition: A list of numbers with a magnitude and a direction. ○ Magnitude: a = [4,3] |a| =sqrt(4^2+3^2)= 5 ○ Direction: angle vector points ● Computer Science Definition: A list of numbers. ○ Example: Heights = [60, 68, 72, 67] Dot Product of Vectors Formula: a · b = |a| × |b| × cos(θ) ● Definition: Multiplication of two vectors which results in a scalar value ● In the diagram: ○ |a| is the magnitude (length) of vector a ○ |b| is the magnitude of vector b ○ Θ is the angle between a and b Matrix ● Definition: ● Matrix elements: ● a)Matrix is an arrangement of numbers into rows and columns. ● b) A matrix is an m × n array of scalars from a given field F. The individual values in the matrix are called entries. ● Matrix dimensions: the number of rows and columns of the matrix, in that order. Multiplication of Matrices ● The multiplication of two matrices ● Result matrix dimensions ○ Notation: (Row, Column) ○ Columns of the 1st matrix must equal the rows of the 2nd matrix ○ Result matrix is equal to the number of (1, 2, 3) • (7, 9, 11) = 1×7 +2×9 + 3×11 rows in 1st matrix and the number of = 58 columns in the 2nd matrix ○ Ex. 3 x 4 ॱ 5 x 3 ■ Dot product does not work ○ Ex. 5 x 3 ॱ 3 x 4 ■ Dot product does work ■ Result: 5 x 4 Dot Product Application ● Application: Ray tracing program ○ Quickly create an image with lower quality ○ “Refinement rendering pass” occurs ■ Removes the jagged edges ○ Dot product used to calculate ■ Intersection between a ray and a sphere ■ Measure the length to the intersection points ● Application: Forward Propagation ○ Input matrix * weighted matrix = prediction matrix http://immersivemath.com/ila/ch03_dotprodu ct/ch03.html#fig_dp_ray_tracer Projections One important use of dot products is in projections.
    [Show full text]
  • Euclidean Space - Wikipedia, the Free Encyclopedia Page 1 of 5
    Euclidean space - Wikipedia, the free encyclopedia Page 1 of 5 Euclidean space From Wikipedia, the free encyclopedia In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions. The term “Euclidean” distinguishes these spaces from the curved spaces of non-Euclidean geometry and Einstein's general theory of relativity, and is named for the Greek mathematician Euclid of Alexandria. Classical Greek geometry defined the Euclidean plane and Euclidean three-dimensional space using certain postulates, while the other properties of these spaces were deduced as theorems. In modern mathematics, it is more common to define Euclidean space using Cartesian coordinates and the ideas of analytic geometry. This approach brings the tools of algebra and calculus to bear on questions of geometry, and Every point in three-dimensional has the advantage that it generalizes easily to Euclidean Euclidean space is determined by three spaces of more than three dimensions. coordinates. From the modern viewpoint, there is essentially only one Euclidean space of each dimension. In dimension one this is the real line; in dimension two it is the Cartesian plane; and in higher dimensions it is the real coordinate space with three or more real number coordinates. Thus a point in Euclidean space is a tuple of real numbers, and distances are defined using the Euclidean distance formula. Mathematicians often denote the n-dimensional Euclidean space by , or sometimes if they wish to emphasize its Euclidean nature. Euclidean spaces have finite dimension. Contents 1 Intuitive overview 2 Real coordinate space 3 Euclidean structure 4 Topology of Euclidean space 5 Generalizations 6 See also 7 References Intuitive overview One way to think of the Euclidean plane is as a set of points satisfying certain relationships, expressible in terms of distance and angle.
    [Show full text]
  • Classical Mechanics Lecture Notes POLAR COORDINATES
    PHYS 419: Classical Mechanics Lecture Notes POLAR COORDINATES A vector in two dimensions can be written in Cartesian coordinates as r = xx^ + yy^ (1) where x^ and y^ are unit vectors in the direction of Cartesian axes and x and y are the components of the vector, see also the ¯gure. It is often convenient to use coordinate systems other than the Cartesian system, in particular we will often use polar coordinates. These coordinates are speci¯ed by r = jrj and the angle Á between r and x^, see the ¯gure. The relations between the polar and Cartesian coordinates are very simple: x = r cos Á y = r sin Á and p y r = x2 + y2 Á = arctan : x The unit vectors of polar coordinate system are denoted by r^ and Á^. The former one is de¯ned accordingly as r r^ = (2) r Since r = r cos Á x^ + r sin Á y^; r^ = cos Á x^ + sin Á y^: The simplest way to de¯ne Á^ is to require it to be orthogonal to r^, i.e., to have r^ ¢ Á^ = 0. This gives the condition cos ÁÁx + sin ÁÁy = 0: 1 The simplest solution is Áx = ¡ sin Á and Áy = cos Á or a solution with signs reversed. This gives Á^ = ¡ sin Á x^ + cos Á y^: This vector has unit length Á^ ¢ Á^ = sin2 Á + cos2 Á = 1: The unit vectors are marked on the ¯gure. With our choice of sign, Á^ points in the direc- tion of increasing angle Á. Notice that r^ and Á^ are drawn from the position of the point considered.
    [Show full text]
  • Distance Between Points on the Earth's Surface
    Distance between Points on the Earth's Surface Abstract During a casual conversation with one of my students, he asked me how one could go about computing the distance between two points on the surface of the Earth, in terms of their respective latitudes and longitudes. This is an interesting exercise in spherical coordinates, and relates to the so-called haversine. The calculation of the distance be- tween two points on the surface of the Spherical coordinates Earth proceeds in two stages: (1) to z compute the \straight-line" Euclidean x=Rcosθcos φ distance these two points (obtained by y=Rcosθsin φ R burrowing through the Earth), and (2) z=Rsinθ to convert this distance to one mea- θ y sured along the surface of the Earth. φ Figure 1 depicts the spherical coor- dinates we shall use.1 We orient this coordinate system so that x Figure 1: Spherical Coordinates (i) The origin is at the Earth's center; (ii) The x-axis passes through the Prime Meridian (0◦ longitude); (iii) The xy-plane contains the Earth's equator (and so the positive z-axis will pass through the North Pole) Note that the angle θ is the measurement of lattitude, and the angle φ is the measurement of longitude, where 0 ≤ φ < 360◦, and −90◦ ≤ θ ≤ 90◦. Negative values of θ correspond to points in the Southern Hemisphere, and positive values of θ correspond to points in the Northern Hemisphere. When one uses spherical coordinates it is typical for the radial distance R to vary; however, in our discussion we may fix it to be the average radius of the Earth: R ≈ 6; 378 km: 1What is depicted are not the usual spherical coordinates, as the angle θ is usually measure from the \zenith", or z-axis.
    [Show full text]