Fixed Point Iteration for Cholesky Factorization of a Tridiagonal Matrix
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
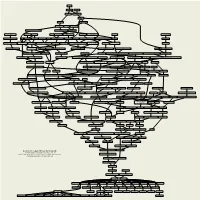
Academic Genealogy of George Em Karniadakis
Nilos Kabasilas Demetrios Kydones Elissaeus Judaeus Manuel Chrysoloras Georgios Plethon Gemistos 1380, 1393 Basilios Bessarion 1436 Mystras Guarino da Verona Johannes Argyropoulos 1408 1444 Università di Padova Vittorino da Feltre Cristoforo Landino Marsilio Ficino 1416 Università di Padova 1462 Università di Firenze Ognibene (Omnibonus Leonicenus) Bonisoli da Lonigo Theodoros Gazes Angelo Poliziano Università di Mantova 1433 Constantinople / Università di Mantova 1477 Università di Firenze Leo Outers Alessandro Sermoneta Gaetano da Thiene Moses Perez Scipione Fortiguerra Demetrios Chalcocondyles Jacob ben Jehiel Loans Rudolf Agricola Thomas à Kempis Heinrich von Langenstein 1485 Université Catholique de Louvain 1493 Università di Firenze 1452 Mystras / Accademia Romana 1478 Università degli Studi di Ferrara 1363, 1375 Université de Paris Maarten (Martinus Dorpius) van Dorp Pelope Pietro Roccabonella Nicoletto Vernia François Dubois Jean Tagault Girolamo (Hieronymus Aleander) Aleandro Janus Lascaris Matthaeus Adrianus Johann (Johannes Kapnion) Reuchlin Jan Standonck Alexander Hegius Johannes von Gmunden 1504, 1515 Université Catholique de Louvain Università di Padova Università di Padova 1516 Université de Paris 1499, 1508 Università di Padova 1472 Università di Padova 1477, 1481 Universität Basel / Université de Poitiers 1474, 1490 Collège Sainte-Barbe / Collège de Montaigu 1474 1406 Universität Wien Niccolò Leoniceno Jacobus (Jacques Masson) Latomus Desiderius Erasmus Petrus (Pieter de Corte) Curtius Pietro Pomponazzi Jacobus (Jacques -

Hilbert Constance Reid
Hilbert Constance Reid Hilbert c COPERNICUS AN IMPRINT OF SPRINGER-VERLAG © 1996 Springer Science+Business Media New York Originally published by Springer-Verlag New York, Inc in 1996 All rights reserved. No part ofthis publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Library ofCongress Cataloging·in-Publication Data Reid, Constance. Hilbert/Constance Reid. p. Ctn. Originally published: Berlin; New York: Springer-Verlag, 1970. Includes bibliographical references and index. ISBN 978-0-387-94674-0 ISBN 978-1-4612-0739-9 (eBook) DOI 10.1007/978-1-4612-0739-9 I. Hilbert, David, 1862-1943. 2. Mathematicians-Germany Biography. 1. Title. QA29.HsR4 1996 SIO'.92-dc20 [B] 96-33753 Manufactured in the United States of America. Printed on acid-free paper. 9 8 7 6 543 2 1 ISBN 978-0-387-94674-0 SPIN 10524543 Questions upon Rereading Hilbert By 1965 I had written several popular books, such as From liro to Infinity and A Long Way from Euclid, in which I had attempted to explain certain easily grasped, although often quite sophisticated, mathematical ideas for readers very much like myself-interested in mathematics but essentially untrained. At this point, with almost no mathematical training and never having done any bio graphical writing, I became determined to write the life of David Hilbert, whom many considered the profoundest mathematician of the early part of the 20th century. Now, thirty years later, rereading Hilbert, certain questions come to my mind. -
![Positional Notation Or Trigonometry [2, 13]](https://docslib.b-cdn.net/cover/6799/positional-notation-or-trigonometry-2-13-106799.webp)
Positional Notation Or Trigonometry [2, 13]
The Greatest Mathematical Discovery? David H. Bailey∗ Jonathan M. Borweiny April 24, 2011 1 Introduction Question: What mathematical discovery more than 1500 years ago: • Is one of the greatest, if not the greatest, single discovery in the field of mathematics? • Involved three subtle ideas that eluded the greatest minds of antiquity, even geniuses such as Archimedes? • Was fiercely resisted in Europe for hundreds of years after its discovery? • Even today, in historical treatments of mathematics, is often dismissed with scant mention, or else is ascribed to the wrong source? Answer: Our modern system of positional decimal notation with zero, to- gether with the basic arithmetic computational schemes, which were discov- ered in India prior to 500 CE. ∗Bailey: Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. Email: [email protected]. This work was supported by the Director, Office of Computational and Technology Research, Division of Mathematical, Information, and Computational Sciences of the U.S. Department of Energy, under contract number DE-AC02-05CH11231. yCentre for Computer Assisted Research Mathematics and its Applications (CARMA), University of Newcastle, Callaghan, NSW 2308, Australia. Email: [email protected]. 1 2 Why? As the 19th century mathematician Pierre-Simon Laplace explained: It is India that gave us the ingenious method of expressing all numbers by means of ten symbols, each symbol receiving a value of position as well as an absolute value; a profound and important idea which appears so simple to us now that we ignore its true merit. But its very sim- plicity and the great ease which it has lent to all computations put our arithmetic in the first rank of useful inventions; and we shall appre- ciate the grandeur of this achievement the more when we remember that it escaped the genius of Archimedes and Apollonius, two of the greatest men produced by antiquity. -

History of Mathematics in Mathematics Education. Recent Developments Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang
History of mathematics in mathematics education. Recent developments Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang To cite this version: Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang. History of mathematics in mathematics education. Recent developments. History and Pedagogy of Mathematics, Jul 2016, Montpellier, France. hal-01349230 HAL Id: hal-01349230 https://hal.archives-ouvertes.fr/hal-01349230 Submitted on 27 Jul 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. HISTORY OF MATHEMATICS IN MATHEMATICS EDUCATION Recent developments Kathleen CLARK, Tinne Hoff KJELDSEN, Sebastian SCHORCHT, Constantinos TZANAKIS, Xiaoqin WANG School of Teacher Education, Florida State University, Tallahassee, FL 32306-4459, USA [email protected] Department of Mathematical Sciences, University of Copenhagen, Denmark [email protected] Justus Liebig University Giessen, Germany [email protected] Department of Education, University of Crete, Rethymnon 74100, Greece [email protected] Department of Mathematics, East China Normal University, China [email protected] ABSTRACT This is a survey on the recent developments (since 2000) concerning research on the relations between History and Pedagogy of Mathematics (the HPM domain). Section 1 explains the rationale of the study and formulates the key issues. -

Pioneers of Representation Theory, by Charles W
BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY Volume 37, Number 3, Pages 359{362 S 0273-0979(00)00867-3 Article electronically published on February 16, 2000 Pioneers of representation theory, by Charles W. Curtis, Amer. Math. Soc., Prov- idence, RI, 1999, xvi + 287 pp., $49.00, ISBN 0-8218-9002-6 The theory of linear representations of finite groups emerged in a series of papers by Frobenius appearing in 1896{97. This was at first couched in the language of characters but soon evolved into the formulation now considered standard, in which characters give the traces of representing linear transformations. There were of course antecedents in the number-theoretic work of Lagrange, Gauss, and others| especially Dedekind, whose correspondence with Frobenius suggested a way to move from characters of abelian groups to characters of arbitrary finite groups. In the past century this theory has developed in many interesting directions. Besides being a natural tool in the study of the structure of finite groups, it has turned up in many branches of mathematics and has found extensive applications in chemistry and physics. Marking the end of the first century of the subject, the book under review offers a somewhat unusual blend of history, biography, and mathematical exposition. Before discussing the book itself, it may be worthwhile to pose a general question: Does one need to know anything about the history of mathematics (or the lives of individual mathematicians) in order to appreciate the subject matter? Most of us are complacent about quoting the usual sloppy misattributions of famous theorems, even if we are finicky about the details of proofs. -

Classics in Mathematics Richard Courant· Fritz John Introduction To
Classics in Mathematics Richard Courant· Fritz John Introduction to Calculus and Analysis Volume I Springer-V erlag Berlin Heidelberg GmbH Richard Courant • Fritz John Introd uction to Calculus and Analysis Volume I Reprint of the 1989 Edition Springer Originally published in 1965 by Interscience Publishers, a division of John Wiley and Sons, Inc. Reprinted in 1989 by Springer-Verlag New York, Inc. Mathematics Subject Classification (1991): 26-XX, 26-01 Cataloging in Publication Data applied for Die Deutsche Bibliothek - CIP-Einheitsaufnahme Courant, Richard: Introduction to calcu1us and analysis / Richard Courant; Fritz John.- Reprint of the 1989 ed.- Berlin; Heidelberg; New York; Barcelona; Hong Kong; London; Milan; Paris; Singapore; Tokyo: Springer (Classics in mathematics) VoL 1 (1999) ISBN 978-3-540-65058-4 ISBN 978-3-642-58604-0 (eBook) DOI 10.1007/978-3-642-58604-0 Photograph of Richard Courant from: C. Reid, Courant in Gottingen and New York. The Story of an Improbable Mathematician, Springer New York, 1976 Photograph of Fritz John by kind permission of The Courant Institute of Mathematical Sciences, New York ISSN 1431-0821 This work is subject to copyright. All rights are reserved. whether the whole or part of the material is concemed. specifically the rights of trans1ation. reprinting. reuse of illustrations. recitation. broadcasting. reproduction on microfilm or in any other way. and storage in data banks. Duplication of this publication or parts thereof is permitted onlyunder the provisions of the German Copyright Law of September 9.1965. in its current version. and permission for use must always be obtained from Springer-Verlag. Violations are Iiable for prosecution under the German Copyright Law. -

A Century of Mathematics in America, Peter Duren Et Ai., (Eds.), Vol
Garrett Birkhoff has had a lifelong connection with Harvard mathematics. He was an infant when his father, the famous mathematician G. D. Birkhoff, joined the Harvard faculty. He has had a long academic career at Harvard: A.B. in 1932, Society of Fellows in 1933-1936, and a faculty appointmentfrom 1936 until his retirement in 1981. His research has ranged widely through alge bra, lattice theory, hydrodynamics, differential equations, scientific computing, and history of mathematics. Among his many publications are books on lattice theory and hydrodynamics, and the pioneering textbook A Survey of Modern Algebra, written jointly with S. Mac Lane. He has served as president ofSIAM and is a member of the National Academy of Sciences. Mathematics at Harvard, 1836-1944 GARRETT BIRKHOFF O. OUTLINE As my contribution to the history of mathematics in America, I decided to write a connected account of mathematical activity at Harvard from 1836 (Harvard's bicentennial) to the present day. During that time, many mathe maticians at Harvard have tried to respond constructively to the challenges and opportunities confronting them in a rapidly changing world. This essay reviews what might be called the indigenous period, lasting through World War II, during which most members of the Harvard mathe matical faculty had also studied there. Indeed, as will be explained in §§ 1-3 below, mathematical activity at Harvard was dominated by Benjamin Peirce and his students in the first half of this period. Then, from 1890 until around 1920, while our country was becoming a great power economically, basic mathematical research of high quality, mostly in traditional areas of analysis and theoretical celestial mechanics, was carried on by several faculty members. -

Real Proofs of Complex Theorems (And Vice Versa)
REAL PROOFS OF COMPLEX THEOREMS (AND VICE VERSA) LAWRENCE ZALCMAN Introduction. It has become fashionable recently to argue that real and complex variables should be taught together as a unified curriculum in analysis. Now this is hardly a novel idea, as a quick perusal of Whittaker and Watson's Course of Modern Analysis or either Littlewood's or Titchmarsh's Theory of Functions (not to mention any number of cours d'analyse of the nineteenth or twentieth century) will indicate. And, while some persuasive arguments can be advanced in favor of this approach, it is by no means obvious that the advantages outweigh the disadvantages or, for that matter, that a unified treatment offers any substantial benefit to the student. What is obvious is that the two subjects do interact, and interact substantially, often in a surprising fashion. These points of tangency present an instructor the opportunity to pose (and answer) natural and important questions on basic material by applying real analysis to complex function theory, and vice versa. This article is devoted to several such applications. My own experience in teaching suggests that the subject matter discussed below is particularly well-suited for presentation in a year-long first graduate course in complex analysis. While most of this material is (perhaps by definition) well known to the experts, it is not, unfortunately, a part of the common culture of professional mathematicians. In fact, several of the examples arose in response to questions from friends and colleagues. The mathematics involved is too pretty to be the private preserve of specialists. -

Robert De Montessus De Ballore's 1902 Theorem on Algebraic
Robert de Montessus de Ballore’s 1902 theorem on algebraic continued fractions : genesis and circulation Hervé Le Ferrand ∗ October 31, 2018 Abstract Robert de Montessus de Ballore proved in 1902 his famous theorem on the convergence of Padé approximants of meromorphic functions. In this paper, we will first describe the genesis of the theorem, then investigate its circulation. A number of letters addressed to Robert de Montessus by different mathematicians will be quoted to help determining the scientific context and the steps that led to the result. In particular, excerpts of the correspondence with Henri Padé in the years 1901-1902 played a leading role. The large number of authors who mentioned the theorem soon after its derivation, for instance Nörlund and Perron among others, indicates a fast circulation due to factors that will be thoroughly explained. Key words Robert de Montessus, circulation of a theorem, algebraic continued fractions, Padé’s approximants. MSC : 01A55 ; 01A60 1 Introduction This paper aims to study the genesis and circulation of the theorem on convergence of algebraic continued fractions proven by the French mathematician Robert de Montessus de Ballore (1870-1937) in 1902. The main issue is the following : which factors played a role in the elaboration then the use of this new result ? Inspired by the study of Sturm’s theorem by Hourya Sinaceur [52], the scientific context of Robert de Montessus’ research will be described. Additionally, the correlation with the other topics on which he worked will be highlighted, -

Oral Presentation
Oral Presentation A LOOK AT OTTO TOEPLITZ’S (1927) “THE PROBLEM OF UNIVERSITY INFINITESIMAL CALCULUS COURSES AND THEIR DEMARCATION FROM INFINITESIMAL CALCULUS IN HIGH SCHOOLS”1 Michael N. Frieda & Hans Niels Jahnkeb aBen Gurion University of the Negev, bUniversität Duisburg-Essen This paper discusses Otto Toeplitz’s 1927 paper “The problem of university infinitesimal calculus courses and their demarcation from infinitesimal calculus in high schools.” The “genetic approach” presented in Toeplitz’s paper is still of interest to mathematics educators who wish to use the history of mathematics in their teaching, for it suggests a rationale for studying history that does not trivialize history of mathematics and shows how history of mathematics can supply not only content for mathematics teaching but also, as Toeplitz is at pains to emphasize, a guide for examining pedagogical problems. At the same time, as we shall discuss in our paper, an attentive reading of Toeplitz’s paper brings out tensions and assumptions about mathematics, history of mathematics and historiography. TOEPLITZ’S LIFE IN MATHEMATICS, HISTORY OF MATHEMATICS, AND MATHEMATICS TEACHING Before starting our examination of the paper which is our focus in this paper, we ought to have some sense of who its author, Otto Toeplitz, was as an intellectual and educational figure. Toeplitz was born in Breslau, Germany (now, Wrocław, Poland) in 1881 and died in Jerusalem in 1940. His doctoral dissertation, Über Systeme von Formen, deren Funktionaldeterminante identisch verschwindet (On Systems of Forms whose Functional Determinant Vanishes Identically) was written under the direction of Jacob Rosanes and Friedrich Otto Rudolf Sturm at the University of Breslau in 1905. -

Mathematicians Fleeing from Nazi Germany
Mathematicians Fleeing from Nazi Germany Mathematicians Fleeing from Nazi Germany Individual Fates and Global Impact Reinhard Siegmund-Schultze princeton university press princeton and oxford Copyright 2009 © by Princeton University Press Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540 In the United Kingdom: Princeton University Press, 6 Oxford Street, Woodstock, Oxfordshire OX20 1TW All Rights Reserved Library of Congress Cataloging-in-Publication Data Siegmund-Schultze, R. (Reinhard) Mathematicians fleeing from Nazi Germany: individual fates and global impact / Reinhard Siegmund-Schultze. p. cm. Includes bibliographical references and index. ISBN 978-0-691-12593-0 (cloth) — ISBN 978-0-691-14041-4 (pbk.) 1. Mathematicians—Germany—History—20th century. 2. Mathematicians— United States—History—20th century. 3. Mathematicians—Germany—Biography. 4. Mathematicians—United States—Biography. 5. World War, 1939–1945— Refuges—Germany. 6. Germany—Emigration and immigration—History—1933–1945. 7. Germans—United States—History—20th century. 8. Immigrants—United States—History—20th century. 9. Mathematics—Germany—History—20th century. 10. Mathematics—United States—History—20th century. I. Title. QA27.G4S53 2008 510.09'04—dc22 2008048855 British Library Cataloging-in-Publication Data is available This book has been composed in Sabon Printed on acid-free paper. ∞ press.princeton.edu Printed in the United States of America 10 987654321 Contents List of Figures and Tables xiii Preface xvii Chapter 1 The Terms “German-Speaking Mathematician,” “Forced,” and“Voluntary Emigration” 1 Chapter 2 The Notion of “Mathematician” Plus Quantitative Figures on Persecution 13 Chapter 3 Early Emigration 30 3.1. The Push-Factor 32 3.2. The Pull-Factor 36 3.D. -

From the Collections of the Seeley G. Mudd Manuscript Library, Princeton, NJ
From the collections of the Seeley G. Mudd Manuscript Library, Princeton, NJ These documents can only be used for educational and research purposes (“Fair use”) as per U.S. Copyright law (text below). By accessing this file, all users agree that their use falls within fair use as defined by the copyright law. They further agree to request permission of the Princeton University Library (and pay any fees, if applicable) if they plan to publish, broadcast, or otherwise disseminate this material. This includes all forms of electronic distribution. Inquiries about this material can be directed to: Seeley G. Mudd Manuscript Library 65 Olden Street Princeton, NJ 08540 609-258-6345 609-258-3385 (fax) [email protected] U.S. Copyright law test The copyright law of the United States (Title 17, United States Code) governs the making of photocopies or other reproductions of copyrighted material. Under certain conditions specified in the law, libraries and archives are authorized to furnish a photocopy or other reproduction. One of these specified conditions is that the photocopy or other reproduction is not to be “used for any purpose other than private study, scholarship or research.” If a user makes a request for, or later uses, a photocopy or other reproduction for purposes in excess of “fair use,” that user may be liable for copyright infringement. The Princeton Mathematics Community in the 1930s Transcript Number 11 (PMC11) © The Trustees of Princeton University, 1985 MERRILL FLOOD (with ALBERT TUCKER) This is an interview of Merrill Flood in San Francisco on 14 May 1984. The interviewer is Albert Tucker.