INCOME and SUBSTITUTION EFFECTS Two Demand Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
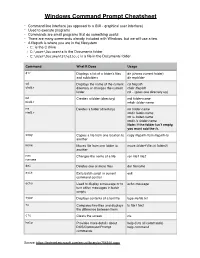
Windows Command Prompt Cheatsheet
Windows Command Prompt Cheatsheet - Command line interface (as opposed to a GUI - graphical user interface) - Used to execute programs - Commands are small programs that do something useful - There are many commands already included with Windows, but we will use a few. - A filepath is where you are in the filesystem • C: is the C drive • C:\user\Documents is the Documents folder • C:\user\Documents\hello.c is a file in the Documents folder Command What it Does Usage dir Displays a list of a folder’s files dir (shows current folder) and subfolders dir myfolder cd Displays the name of the current cd filepath chdir directory or changes the current chdir filepath folder. cd .. (goes one directory up) md Creates a folder (directory) md folder-name mkdir mkdir folder-name rm Deletes a folder (directory) rm folder-name rmdir rmdir folder-name rm /s folder-name rmdir /s folder-name Note: if the folder isn’t empty, you must add the /s. copy Copies a file from one location to copy filepath-from filepath-to another move Moves file from one folder to move folder1\file.txt folder2\ another ren Changes the name of a file ren file1 file2 rename del Deletes one or more files del filename exit Exits batch script or current exit command control echo Used to display a message or to echo message turn off/on messages in batch scripts type Displays contents of a text file type myfile.txt fc Compares two files and displays fc file1 file2 the difference between them cls Clears the screen cls help Provides more details about help (lists all commands) DOS/Command Prompt help command commands Source: https://technet.microsoft.com/en-us/library/cc754340.aspx. -

Mac Keyboard Shortcuts Cut, Copy, Paste, and Other Common Shortcuts
Mac keyboard shortcuts By pressing a combination of keys, you can do things that normally need a mouse, trackpad, or other input device. To use a keyboard shortcut, hold down one or more modifier keys while pressing the last key of the shortcut. For example, to use the shortcut Command-C (copy), hold down Command, press C, then release both keys. Mac menus and keyboards often use symbols for certain keys, including the modifier keys: Command ⌘ Option ⌥ Caps Lock ⇪ Shift ⇧ Control ⌃ Fn If you're using a keyboard made for Windows PCs, use the Alt key instead of Option, and the Windows logo key instead of Command. Some Mac keyboards and shortcuts use special keys in the top row, which include icons for volume, display brightness, and other functions. Press the icon key to perform that function, or combine it with the Fn key to use it as an F1, F2, F3, or other standard function key. To learn more shortcuts, check the menus of the app you're using. Every app can have its own shortcuts, and shortcuts that work in one app may not work in another. Cut, copy, paste, and other common shortcuts Shortcut Description Command-X Cut: Remove the selected item and copy it to the Clipboard. Command-C Copy the selected item to the Clipboard. This also works for files in the Finder. Command-V Paste the contents of the Clipboard into the current document or app. This also works for files in the Finder. Command-Z Undo the previous command. You can then press Command-Shift-Z to Redo, reversing the undo command. -
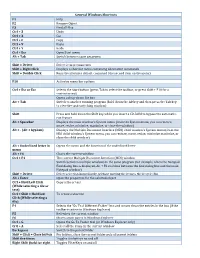
General Windows Shortcuts
General Windows Shortcuts F1 Help F2 Rename Object F3 Find all files Ctrl + Z Undo Ctrl + X Cut Ctrl + C Copy Ctrl + V Paste Ctrl + Y Redo Ctrl + Esc Open Start menu Alt + Tab Switch between open programs Alt + F4 Quit program Shift + Delete Delete item permanently Shift + Right Click Displays a shortcut menu containing alternative commands Shift + Double Click Runs the alternate default command ( the second item on the menu) Alt + Double Click Displays properties F10 Activates menu bar options Shift + F10 Opens a contex t menu ( same as righ t click) Ctrl + Esc or Esc Selects the Start button (press Tab to select the taskbar, or press Shift + F10 for a context menu) Alt + Down Arrow Opens a drop‐down list box Alt + Tab Switch to another running program (hold down the Alt key and then press the Tab key to view the task‐switching window) Alt + Shift + Tab Swit ch b ackward s b etween open appli cati ons Shift Press and hold down the Shift key while you insert a CD‐ROM to bypass the automatic‐ run feature Alt + Spacebar Displays the main window's System menu (from the System menu, you can restore, move, resize, minimize, maximize, or close the window) Alt + (Alt + hyphen) Displays the Multiple Document Interface (MDI) child window's System menu (from the MDI child window's System menu, you can restore, move, resize, minimize maximize, or close the child window) Ctrl + Tab Switch to t h e next child window o f a Multi ple D ocument Interf ace (MDI) pr ogram Alt + Underlined letter in Opens the menu and the function of the underlined letter -

Substitution and Income Effect
Intermediate Microeconomic Theory: ECON 251:21 Substitution and Income Effect Alternative to Utility Maximization We have examined how individuals maximize their welfare by maximizing their utility. Diagrammatically, it is like moderating the individual’s indifference curve until it is just tangent to the budget constraint. The individual’s choice thus selected gives us a demand for the goods in terms of their price, and income. We call such a demand function a Marhsallian Demand function. In general mathematical form, letting x be the quantity of a good demanded, we write the Marshallian Demand as x M ≡ x M (p, y) . Thinking about the process, we can reverse the intuition about how individuals maximize their utility. Consider the following, what if we fix the utility value at the above level, but instead vary the budget constraint? Would we attain the same choices? Well, we should, the demand thus achieved is however in terms of prices and utility, and not income. We call such a demand function, a Hicksian Demand, x H ≡ x H (p,u). This method means that the individual’s problem is instead framed as minimizing expenditure subject to a particular level of utility. Let’s examine briefly how the problem is framed, min p1 x1 + p2 x2 subject to u(x1 ,x2 ) = u We refer to this problem as expenditure minimization. We will however not consider this, safe to note that this problem generates a parallel demand function which we refer to as Hicksian Demand, also commonly referred to as the Compensated Demand. Decomposition of Changes in Choices induced by Price Change Let’s us examine the decomposition of a change in consumer choice as a result of a price change, something we have talked about earlier. -

Powerview Command Reference
PowerView Command Reference TRACE32 Online Help TRACE32 Directory TRACE32 Index TRACE32 Documents ...................................................................................................................... PowerView User Interface ............................................................................................................ PowerView Command Reference .............................................................................................1 History ...................................................................................................................................... 12 ABORT ...................................................................................................................................... 13 ABORT Abort driver program 13 AREA ........................................................................................................................................ 14 AREA Message windows 14 AREA.CLEAR Clear area 15 AREA.CLOSE Close output file 15 AREA.Create Create or modify message area 16 AREA.Delete Delete message area 17 AREA.List Display a detailed list off all message areas 18 AREA.OPEN Open output file 20 AREA.PIPE Redirect area to stdout 21 AREA.RESet Reset areas 21 AREA.SAVE Save AREA window contents to file 21 AREA.Select Select area 22 AREA.STDERR Redirect area to stderr 23 AREA.STDOUT Redirect area to stdout 23 AREA.view Display message area in AREA window 24 AutoSTOre .............................................................................................................................. -

S.Ha.R.K. Installation Howto Tools Knoppix Live CD Linux Fdisk HD
S.Ha.R.K. Installation Tools HowTo • Linux fdisk utility • A copy of Linux installation CD • A copy of Windows® installation CD Tullio Facchinetti University of Pavia - Italy • Some FreeDOS utilities • A copy of S.Ha.R.K. S.Ha.R.K. Workshop S.Ha.R.K. Workshop Knoppix live CD Linux fdisk Command action a toggle a bootable flag Download ISO from b edit bsd disklabel c toggle the dos compatibility flag d delete a partition http://www.knoppix.org l list known partition types m print this menu n add a new partition o create a new empty DOS partition table p print the partition table q quit without saving changes • boot from CD s create a new empty Sun disklabel t change a partition's system id • open a command shell u change display/entry units v verify the partition table • type “su” (become root ), password is empty w write table to disk and exit x extra functionality (experts only) • start fdisk (ex. fdisk /dev/hda ) Command (m for help): S.Ha.R.K. Workshop S.Ha.R.K. Workshop HD partitioning HD partitioning 1st FreeDOS FAT32 FreeDOS must be installed Primary 2nd Windows® FAT32 into the first partition of your HD or it may not boot 3rd Linux / extX Data 1 FAT32 format data partitions as ... Extended FAT32, so that you can share Data n FAT32 your data between Linux, last Linux swap swap Windows® and FreeDOS S.Ha.R.K. Workshop S.Ha.R.K. Workshop 1 HD partitioning Windows ® installation FAT32 Windows® partition type Install Windows®.. -

Principles of Economics1 3
Income and working hours across time and countries Scarcity and choice: key concepts Decision-making under scarcity Concluding remarks and summary Principles of Economics1 3. Scarcity, work, and choice Giuseppe Vittucci Marzetti2 SCOR Department of Sociology and Social Research University of Milano-Bicocca A.Y. 2018-19 1These slides are based on the material made available under Creative Commons BY-NC-ND © 4.0 by the CORE Project , https://www.core-econ.org/. 2Department of Sociology and Social Research, University of Milano-Bicocca, Via Bicocca degli Arcimboldi 8, 20126, Milan, E-mail: [email protected] Giuseppe Vittucci Marzetti Principles of Economics 1/26 Income and working hours across time and countries Scarcity and choice: key concepts Decision-making under scarcity Concluding remarks and summary Layout 1 Income and working hours across time and countries 2 Scarcity and choice: key concepts Production function, average productivity and marginal productivity Preferences and indifference curves Opportunity cost Feasible frontier 3 Decision-making under scarcity Constrained choices and optimal decision making Labor choice Income effect and substitution effect Effect of technological change on labor choices 4 Concluding remarks and summary Concluding remarks Summary Giuseppe Vittucci Marzetti Principles of Economics 2/26 Income and working hours across time and countries Scarcity and choice: key concepts Decision-making under scarcity Concluding remarks and summary Income and free time across countries Figure: Annual hours of free time per worker and income (2013) Giuseppe Vittucci Marzetti Principles of Economics 3/26 Income and working hours across time and countries Scarcity and choice: key concepts Decision-making under scarcity Concluding remarks and summary Income and working hours across time and countries Figure: Annual hours of work and income (18702000) Living standards have greatly increased since 1870. -

What Impact Does Scarcity Have on the Production, Distribution, and Consumption of Goods and Services?
Curriculum: 2009 Pequea Valley SD Curriculum PEQUEA VALLEY SD Course: Social Studies 12 Date: May 25, 2010 ET Topic: Foundations of Economics Days: 10 Subject(s): Grade(s): Key Learning: The exchange of goods and services provides choices through which people can fill their basic needs and wants. Unit Essential Question(s): What impact does scarcity have on the production, distribution, and consumption of goods and services? Concept: Concept: Concept: Scarcity Factors of Production Opportunity Cost 6.2.12.A, 6.5.12.D, 6.5.12.F 6.3.12.E 6.3.12.E, 6.3.12.B Lesson Essential Question(s): Lesson Essential Question(s): Lesson Essential Question(s): What is the problem of scarcity? (A) What are the four factors of production? (A) How does opportunity cost affect my life? (A) (A) What role do you play in the circular flow of economic activity? (ET) What choices do I make in my individual spending habits and what are the opportunity costs? (ET) Vocabulary: Vocabulary: Vocabulary: scarcity, economics, need, want, land, labor, capital, entrepreneurship, factor trade-offs, opportunity cost, production markets, product markets, economic growth possibility frontier, economic models, cost benefit analysis Concept: Concept: Concept: Economic Systems Economic and Social Goals Free Enterprise 6.1.12.A, 6.2.12.A 6.2.12.I, 6.2.12.A, 6.2.12.B, 6.1.12.A, 6.4.12.B 6.2.12.I Lesson Essential Question(s): Lesson Essential Question(s): Lesson Essential Question(s): Which ecoomic system offers you the most What is the most and least important of the To what extent -

KEYBOARD SHORTCUTS (Windows)
KEYBOARD SHORTCUTS (Windows) Note: For Mac users, please substitute the Command key for the Ctrl key. This substitution with work for the majority of commands _______________________________________________________________________ General Commands Navigation Windows key + D Desktop to foreground Context menu Right click Alt + underlined letter Menu drop down, Action selection Alt + Tab Toggle between open applications Alt, F + X or Alt + F4 Exit application Alt, Spacebar + X Maximize window Alt, Spacebar + N Minimize window Ctrl + W Closes window F2 Renames a selected file or folder Open Programs To open programs from START menu: Create a program shortcut and drop it into START menu To open programs/files on Desktop: Select first letter, and then press Enter to open Dialog Boxes Enter Selects highlighted button Tab Selects next button Arrow keys Selects next (>) or previous button (<) Shift + Tab Selects previous button _______________________________________________________________________ Microsoft Word Formatting Ctrl + P Print Ctrl + S Save Ctrl + Z Undo Ctrl + Y Redo CTRL+B Make text bold CTRL+I Italicize CTRL+U Underline Ctrl + C Copy Ctrl + V Paste Ctrl + X Copy + delete Shift + F3 Change case of letters Ctrl+Shift+> Increase font size Ctrl+Shift+< Decrease font size Highlight Text Shift + Arrow Keys Selects one letter at a time Shift + Ctrl + Arrow keys Selects one word at a time Shift + End or Home Selects lines of text Change or resize the font CTRL+SHIFT+ > Increase the font size 1 KEYBOARD SHORTCUTS (Windows) CTRL+SHIFT+ < -

AP Macroeconomics: Vocabulary 1. Aggregate Spending (GDP)
AP Macroeconomics: Vocabulary 1. Aggregate Spending (GDP): The sum of all spending from four sectors of the economy. GDP = C+I+G+Xn 2. Aggregate Income (AI) :The sum of all income earned by suppliers of resources in the economy. AI=GDP 3. Nominal GDP: the value of current production at the current prices 4. Real GDP: the value of current production, but using prices from a fixed point in time 5. Base year: the year that serves as a reference point for constructing a price index and comparing real values over time. 6. Price index: a measure of the average level of prices in a market basket for a given year, when compared to the prices in a reference (or base) year. 7. Market Basket: a collection of goods and services used to represent what is consumed in the economy 8. GDP price deflator: the price index that measures the average price level of the goods and services that make up GDP. 9. Real rate of interest: the percentage increase in purchasing power that a borrower pays a lender. 10. Expected (anticipated) inflation: the inflation expected in a future time period. This expected inflation is added to the real interest rate to compensate for lost purchasing power. 11. Nominal rate of interest: the percentage increase in money that the borrower pays the lender and is equal to the real rate plus the expected inflation. 12. Business cycle: the periodic rise and fall (in four phases) of economic activity 13. Expansion: a period where real GDP is growing. 14. Peak: the top of a business cycle where an expansion has ended. -

1 Unit 4. Consumer Choice Learning Objectives to Gain an Understanding of the Basic Postulates Underlying Consumer Choice: U
Unit 4. Consumer choice Learning objectives to gain an understanding of the basic postulates underlying consumer choice: utility, the law of diminishing marginal utility and utility- maximizing conditions, and their application in consumer decision- making and in explaining the law of demand; by examining the demand side of the product market, to learn how incomes, prices and tastes affect consumer purchases; to understand how to derive an individual’s demand curve; to understand how individual and market demand curves are related; to understand how the income and substitution effects explain the shape of the demand curve. Questions for revision: Opportunity cost; Marginal analysis; Demand schedule, own and cross-price elasticities of demand; Law of demand and Giffen good; Factors of demand: tastes and incomes; Normal and inferior goods. 4.1. Total and marginal utility. Preferences: main assumptions. Indifference curves. Marginal rate of substitution Tastes (preferences) of a consumer reveal, which of the bundles X=(x1, x2) and Y=(y1, y2) is better, or gives higher utility. Utility is a correspondence between the quantities of goods consumed and the level of satisfaction of a person: U(x1,x2). Marginal utility of a good shows an increase in total utility due to infinitesimal increase in consumption of the good, provided that consumption of other goods is kept unchanged. and are marginal utilities of the first and the second good correspondingly. Marginal utility shows the slope of a utility curve (see the figure below). The law of diminishing marginal utility (the first Gossen law) states that each extra unit of a good consumed, holding constant consumption of other goods, adds successively less to utility. -

Package 'Move'
Package ‘move’ November 26, 2020 Type Package Title Visualizing and Analyzing Animal Track Data Version 4.0.6 Description Contains functions to access movement data stored in 'movebank.org' as well as tools to visualize and statistically analyze animal movement data, among others functions to calculate dynamic Brownian Bridge Movement Models. Move helps addressing movement ecology questions. License GPL (>= 3) URL https://bartk.gitlab.io/move/ BugReports https://gitlab.com/bartk/move/-/issues LazyLoad yes LazyData yes LazyDataCompression xz Depends geosphere (>= 1.4-3), methods, sp, raster (>= 2.4-15), rgdal, R (>= 3.5.0) Suggests adehabitatHR, adehabitatLT, markdown, rmarkdown, circular, ggmap, mapproj, maptools, testthat, knitr, ggplot2, leaflet, lubridate, ctmm, amt, bcpa, EMbC Imports httr, memoise, xml2, Rcpp LinkingTo Rcpp SystemRequirements C++11 RoxygenNote 7.1.1 VignetteBuilder knitr NeedsCompilation yes Author Bart Kranstauber [aut, cre], Marco Smolla [aut], Anne K Scharf [aut] Maintainer Bart Kranstauber <[email protected]> Repository CRAN Date/Publication 2020-11-26 15:50:06 UTC 1 2 R topics documented: R topics documented: move-package . .3 .UD-class . .5 .unUsedRecords-class . .6 angle . .7 as.data.frame . .8 brownian.bridge.dyn . 10 brownian.motion.variance.dyn . 13 burst............................................. 14 burstId . 15 citations . 16 contour . 17 coordinates . 18 corridor . 18 DBBMM-class . 20 DBBMMBurstStack-class . 22 DBBMMStack-class . 23 dBGBvariance-class . 24 dBMvariance . 25 distance . 26 duplicatedDataExample . 27 dynBGB . 28 dynBGB-class . 30 dynBGBvariance . 31 emd ............................................. 33 equalProj . 35 fishers . 36 getDataRepositoryData . 36 getDuplicatedTimestamps . 37 getMotionVariance . 39 getMovebank . 40 getMovebankAnimals . 43 getMovebankData . 44 getMovebankID . 47 getMovebankLocationData . 48 getMovebankNonLocationData . 51 getMovebankReferenceTable . 53 getMovebankSensors . 54 getMovebankSensorsAttributes . 55 getMovebankStudies .