Nematic Van Der Waals Free Energy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pintu Mondal
CURRICULUM VITAE PINTU MONDAL At-Birinchibari, P.O.-Nafarganj, P.S.-Basanti, Dist.-South 24 Parganas Pin: 743312 Mobile: +919681153154 / +917908025407 E-mail: [email protected] [email protected] Objective To have innovative skills as well as I can strength and satisfy myself by continuous learning. Interest in controlling the chaotic dynamical systems, algebra, real & complex analysis, and in any kind basic mathematics. Personal Details Language Proficiency: Bengali, English. Date of Birth: 03rd February,1988 Father’s Name: Amal Krishna Mondal. Mother’s Name: Mina Rani Mondal. Nationality: Indian. Education Examination Passed University / Year of Name of the School/ College/ University Board Passing M.Sc. C.U 2O11 Ballyguenge Science College B.Sc. C.U 2009 Dinabandhu Andrews College H.S. WBCHSE 2006 Rangabelia High School (H.S) M.P. WBBSE 2004 NafarganjBaidyanathVidyapith Special Papers Differential Structures on a Manifold. Integral Equations and Boundary Value Problems. Other Qualifications Exam. Passed Co-Ordinating Authority Year of Passing Subject NET CSIR-HRDG December-2011 Mathematical Science Status of Services Name of the Institutions Date of Joining Appointing Authority Raghunathpur College, Raghunathpur, Purulia 12/02/2015 WBCSC Ista Badista High School, Chandanpur, Hooghly 06/12/2013 WBSSC Publications / Paper Presentation Title Name of Journal ISSN / ISBN Volume / Page The Integrals of Motion for International Journal of Pure and ISSN 2229 - 16(1) (2013), Modified Chua’s Circuit Applied Sciences and Technology 6107 pp. 54-60 Participation in Workshops/Seminars /RC/OP/Others Date Topics Organized By 04/ 07/ 2017 Participate in 87th Orientation Program by UGC-HRDC HRDC, Ranchi University to 31/ 07/ 2017 22/ 02/ 2017 Workshop on CBCS System (Presented by S.C. -

Kashipur Micheal Madhusudan Mahavidyalaya (Personal Profile)
KASHIPUR MICHEAL MADHUSUDAN MAHAVIDYALAYA (PERSONAL PROFILE) Name: NILKANTHA BOURI Designation: SACT II Department: HISTORY Date of Joining: 07.08.2017 e-mail: [email protected] Educational Qualification: 1. Graduation: B.A (Hons.) in History from Kashipur Michael Madhusudan Mahavidyalaya, Kashipur,Purulia Affiliated To Sidho Kanho Birsha University, 2014 2. Post-graduation: M.A in History from Sidho Kanho University, 2016 State Level / National / International Conferences /Seminars /Workshops /Webinar Attended: A) Paper Presentations in Seminars / Conferences / Webinars 1. NA B) Participation in Seminars / Conferences / Training Programmes / Workshop / Webinars 1. One Day State Level Seminar on “ Bangla Bangali Bangladesh” Organized by Department of History, SidhoKanhoBirsha University on 26thMarch 2015. 2. UGC Sponsored two days National Seminar on “ TRIBAL REBELLION AND LITERATURE IN 18TH AND 19THCENTURY ” Organized by Department of History & Santali , ManbhumMahavidyalaya , Manbazar, Purulia on 29th & 30thApril 2015. 3. State Level Seminar cum workshop on “160 YEARS OF SANTHAL REBELLION” Organized by The Department of History, Kashipur Michael Madhusudan Mahavidyalaya on 26th June 2015 4. U.G.C Sponsored two day National Level Seminar on “Anti-British Movement in South West Bengal:1799-1857 A new Phase of Indian freedom Movement” organized by department of History ,Kashipur Michael Madhusudan Mahavidyalaya, Purulia on 9th-10th dec.2016 5. One Day International Seminar On “VADU & TRADITIONAL VADRA-CULTURE” Organized by Kashipur Michael Madhusudan Mahavidyalaya, kashipur, purulia on 14th sep. 2018 6. International Webinar on “ COVID-19: CHALLENGES AND OPPORTUNITIES” Organized by IQAC Kashipur Michael Madhusudan Mahavidyalaya , Kashipur, Purulia on 5th june 2020 7. Celebration of International Day of Yoga on the topic “IMPORTANCE OF YOGA IN DAILY LIFE” Organized by Kashipur Michael Madhusudan Mahavidyalaya on 21th june 2020 8. -

SR NO First Name Middle Name Last Name Address Pincode Folio
SR NO First Name Middle Name Last Name Address Pincode Folio Amount 1 A SPRAKASH REDDY 25 A D REGIMENT C/O 56 APO AMBALA CANTT 133001 0000IN30047642435822 22.50 2 A THYAGRAJ 19 JAYA CHEDANAGAR CHEMBUR MUMBAI 400089 0000000000VQA0017773 135.00 3 A SRINIVAS FLAT NO 305 BUILDING NO 30 VSNL STAFF QTRS OSHIWARA JOGESHWARI MUMBAI 400102 0000IN30047641828243 1,800.00 4 A PURUSHOTHAM C/O SREE KRISHNA MURTY & SON MEDICAL STORES 9 10 32 D S TEMPLE STREET WARANGAL AP 506002 0000IN30102220028476 90.00 5 A VASUNDHARA 29-19-70 II FLR DORNAKAL ROAD VIJAYAWADA 520002 0000000000VQA0034395 405.00 6 A H SRINIVAS H NO 2-220, NEAR S B H, MADHURANAGAR, KAKINADA, 533004 0000IN30226910944446 112.50 7 A R BASHEER D. NO. 10-24-1038 JUMMA MASJID ROAD, BUNDER MANGALORE 575001 0000000000VQA0032687 135.00 8 A NATARAJAN ANUGRAHA 9 SUBADRAL STREET TRIPLICANE CHENNAI 600005 0000000000VQA0042317 135.00 9 A GAYATHRI BHASKARAAN 48/B16 GIRIAPPA ROAD T NAGAR CHENNAI 600017 0000000000VQA0041978 135.00 10 A VATSALA BHASKARAN 48/B16 GIRIAPPA ROAD T NAGAR CHENNAI 600017 0000000000VQA0041977 135.00 11 A DHEENADAYALAN 14 AND 15 BALASUBRAMANI STREET GAJAVINAYAGA CITY, VENKATAPURAM CHENNAI, TAMILNADU 600053 0000IN30154914678295 1,350.00 12 A AYINAN NO 34 JEEVANANDAM STREET VINAYAKAPURAM AMBATTUR CHENNAI 600053 0000000000VQA0042517 135.00 13 A RAJASHANMUGA SUNDARAM NO 5 THELUNGU STREET ORATHANADU POST AND TK THANJAVUR 614625 0000IN30177414782892 180.00 14 A PALANICHAMY 1 / 28B ANNA COLONY KONAR CHATRAM MALLIYAMPATTU POST TRICHY 620102 0000IN30108022454737 112.50 15 A Vasanthi W/o G -

A Web Lecture Series
A W E B L E C T U R E S E R I E S Studying History O R G A N I S E D B Y D E P A R T M E N T O F H I S T O R Y R A G H U N A T H P U R C O L L E G E Raghunathpur, Purulia-723133, West Bengal 25th August to 31st August 2020 11:00 am to 1:00 pm On Google Meet For more information, please contact programme coordinators Sohini Sinha (7044931430) Swadhin Sarkar (9875444304) "Studying History" is a seven days' lecture series primarily, designed for the under graduate and post graduate students of history. The intention behind this Programme is to arrange a platform for a lively exchange of ideas and initiate thought provoking discussions on diverse range of topics. These series will allow students to communicate with guest speakers and also provide them with the much needed exposure during this time of social distancing. A W E B L E C T U R E S E R I E S Studying DAY 1 (25.8.20 Tuesday) History O R G A N I S E D B Y D E P A R T M E N T O F H I S T O R Y R A G H U N A T H P U R C O L L E G E INAUGURAL SESSION Raghunathpur, Purulia-723133, West Bengal (10:30AM - 11:00 AM) Welcome Address Dr.Phalguni Mukhopadhyay (Principal, Raghunathpur college & Chief patron of lecture series program.) Inaugural Address Dr. -

ANALYSIS of GROWTH PATTERN of LAC INDUSTRY Jyoti Prakash Mandal* Jaydeb Sarkhel**
Vidyasagar University Journal of Commerce Vol. 20, 2015/ISSN 0973-5917 ANALYSIS OF GROWTH PATTERN OF LAC INDUSTRY Jyoti Prakash Mandal* Jaydeb Sarkhel** Abstract In order to study the growth pattern of the lac industry, we have measured trend rate of growth of production by taking three categories of firms namely big size firms, medium size firms and small size firms. For this, prominent five manufacturing firms under each category have been selected. During the period under consideration (i.e. 2000-01 to 2010-11) the production of five big manufacturers had an annual growth of 12.94%. The rate of profit for the big firms remained more or less stable during study period. During the period under consideration (i.e. 2000-01 to 2010-11) the production of five medium manufacturers had an annual growth rate of 2.13%. In respect of five selected small size firms for the period from 2000- 01 to 2010-11, it showed a positive but distinctly declining rate of profit. The trend rate of production over the period has been as high as 2.34%. If we consider the analysis by taking all the 15 firms together, then the analysis will give us the integrated picture of lac industry. From that we can derive the growth pattern of lac industry as a whole. The production of lac manufacturers grew at 10 percent per annum. Key words : Lac Industry of Purulia District (R); Big Size Firms, Medium Size Firms, Small Size Firms, C8); Growth Pattern (C2)Trend Rate of Production(C4) 1. Introduction Lac and its products have a hoary past in the soil of Purulia district. -

Kashipur Micheal Madhusudan Mahavidyalaya (Personal Profile)
KASHIPUR MICHEAL MADHUSUDAN MAHAVIDYALAYA (PERSONAL PROFILE) Name: SAMRAT MAL Designation: SACT Department: EDUCATION Date of Joining: 15/07/2016 E-mail: [email protected] Educational Qualification: 1. Graduation: B.A in Education (Hons) 2012 2. Post-graduation: M.A in Education 2014 3. M.Phil / Ph.D. NO 4. NET/SET: NET in education 2919 State Level / National / International Conferences /Seminars /Workshops /Webinar Attended: A) Paper Presentations in Seminars (state/ National / International level) 1. One day state level seminar on “Present Crisis in Teaching and learning: Revisiting Pedagogy and Ethics”. Organize by the department of Philosophy and Education Nistarini College purulia 28th September, 2018. 2. One day National seminar on “Restructuring Teacher Education Programe for Conjuring the Spirit of Classroom”. Organize by B.B.M B.Ed. College, Sardaha, Chash, Bokaro, Jharkhand on 19th March 2018. 3. One day National seminar on “Research in Teacher Education in the New Millennium”. Organize by Udyog College of Education in Collaboration with Uttaran College of Education, Onda Bishnupur on 8th April 2018. 4. One day National seminar on “Gandhi Legacy in the 21st Century”. Organize by IQAC and NSS units Mahatma Gandhi College Lalpur, Purulia on 3rd October 2018. 5. Two day National seminar on “Value Education in Respect of Present Education scenario”. Organize by Purnadisha Joychandi Teachers’ training College , Raghunathpur, Purulia on 10th & 11th April 2018, 6. One day International seminar on “Vadu & Traditional Vadra – Culture”. Organize by Kashipur Michael Madhusudan Mahavidyalaya, Panchakote Raj, Purulia on 14th September 2018. 7. One day international seminar on “Indigenous Knowledge and Culture: Issues, Challenges and New Directions”. -

Education General Sc St Obc(A) Obc(B) Ph/Vh Total Vacancy 37 44 19 16 17 4 137 General
EDUCATION GENERAL SC ST OBC(A) OBC(B) PH/VH TOTAL VACANCY 37 44 19 16 17 4 137 GENERAL Sl No. University College Total 1 RAJ NAGAR MAHAVIDYALAYA 1 BURDWAN UNIVERSITY 2 SWAMI DHANANJAY DAS KATHIABABA MV, BHARA 1 3 AZAD HIND FOUZ SMRITI MAHAVIDYALAYA 1 4 BARUIPUR COLLEGE 1 5 DHOLA MAHAVIDYALAYA 1 6 HERAMBA CHANDRA COLLEGE 1 7 CALCUTTA UNIVERSITY MAHARAJA SRIS CHANDRA COLLEGE 1 8 SERAMPORE GIRLS' COLLEGE 1 9 SIBANI MANDAL MAHAVIDYALAYA 1 10 SONARPUR MAHAVIDYALAYA 1 11 SUNDARBAN HAZI DESARAT COLLEGE 1 12 GANGARAMPUR COLLEGE 1 13 GOURBANGA UNIVERSITY NATHANIEL MURMU COLLEGE 1 14 SOUTH MALDA COLLEGE 1 15 DUKHULAL NIBARAN CHANDRA COLLEGE 1 16 HAZI A. K. KHAN COLLEGE 1 17 KALYANI UNIVERSITY NUR MOHAMMAD SMRITI MAHAVIDYALAYA 1 18 PLASSEY COLLEGE 1 19 SUBHAS CHADRA BOSE CENTENARY COLLEGE 1 20 CLUNY WOMENS COLLEGE 1 21 LILABATI MAHAVIDYALAYA 1 NORTH BENGAL UNIVERSITY 22 NAKSHALBARI COLLEGE 1 23 RAJGANJ MAHAVIDYALAYA, RAJGANJ 1 24 ARSHA COLLEGE 1 SIDHO KANHO BIRSA UNIVERSITY 25 KOTSHILA MAHAVIDYALAYA 1 26 BHATTER COLLEGE 1 27 GOURAV GUIN MEMORIAL COLLEGE 1 28 PANSKURA BANAMALI COLLEGE 1 VIDYASAGAR UNIVERSITY 29 RABINDRA BHARATI MAHAVIDYALAYA 1 30 SIDDHINATH MAHAVIDYALAYA 1 31 SUKUMAR SENGUPTA MAHAVIDYALAYA 1 32 BARRAKPORE RASHTRAGURU SURENDRANATH COLLEGE 1 33 KALINAGAR MV 1 34 MAHADEVANANDA MAHAVIDYALAYA 1 WEST BENGAL STATE UNIVERSITY 35 NETAJI SATABARSHIKI MAHABIDYALAYA 1 36 P.N.DAS COLLEGE 1 37 RISHI BANKIM CHANDRA COLLEGE FOR WOMEN 1 OBC(A) 1 HOOGHLY WOMEN'S COLLEGE 1 BURDWAN UNIVERSITY 2 KABI JOYDEB MAHAVIDYALAYA 1 3 GANGADHARPUR MAHAVIDYALAYA -

Edited Form for Upload 2
Name Title and Affiliation 1 Jinee Lokaneeta Professor, Drew University 2 Bhavani Raman Associate Professor, University of Toronto 3 Gopal Guru Former Professor, JNU, Editor, EPW 4 Arjun Appadurai Professor, New York University and Hertie School (Berlin) 5 Veena Das Professor, Johns Hopkins University 6 David Harvey Distinguished Professor, The Graduate Center of the City University of New York 7 G N Devy Chairman, People’s Linguistic Survey of India 8 Faisal Devji Professor of Indian History, University of Oxford 9 Chandra Talpade Mohanty Distinguished Professor, Syracuse University 10 Joan Scott Professor Emerita School of Social Science Institute for Advanced Study, Princeton 11 Natalie Zemon Davis Professor of History Emeritus, Princeton University 12 Rajeswari Sunder Rajan Professor, New York University 13 Chayanika Shah Member, LABIA - A Queer Feminist LBT Collective Mumbai 14 Geeta Seshu Joint Founder-Editor, Free Speech Collective 15 Nandita Haksar Advocate and Writer 16 Romila Thapar Professor Emerita, Jawaharlal Nehru University 17 Akeel Bilgrami Professor of Philosophy, Columbia University 18 Alladi Sitaram Professor (Retd.), Indian Statistical Institute 19 Soni Sori Activist, Bastar 20 Nirjhari Sinha Chairperson Jan Sangharsh Manch, Ahmedabad 21 Rajesh Mahapatra Journalist 22 Shabnam Hashmi Founding Trustee, Anhad 23 Ali Kazimi Filmmaker and Associate Professor, York University, Canada 24 V. Geetha Independent Scholar 25 Sugata Bose Gardiner Professor of Oceanic History and Affairs, Harvard University 26 Prof. C. Lakshmanan Dalit Intellectual Collective 27 Saheli- Women's Resource Centre Autonomous Women's Group 28 Anand Patwardhan Filmmaker 29 Rinaldo Walcott Professor, University of Toronto 30 Utsa Patnaik Professor Emeritus, JNU 31 Dolly Kikon Faculty. The University of Melbourne 32 Anjali Monteiro Professor, Tata Institute of Social Sciences 33 Tarun Bhartiya Raiot Collective 34 Partha Chatterjee Professor of Anthropology, Columbia University 35 Jodi Dean Professor, Hobart-William Smith 36 Prabhat Patnaik Professor Emeritus, JNU. -
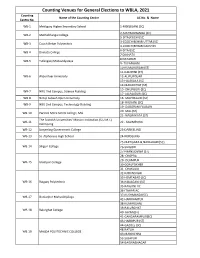
Counting Arrangements WBLA2021.Xlsx
Counting Venues for General Elections to WBLA, 2021 Counting Name of the Counting Centre AC No. & Name Centre No. WB-1 Mekliganj Higher Secondary School 1-MEKLIGANJ (SC) 2-MATHABHANGA (SC) WB-2 Mathabhanga College 5-SITALKUCHI (SC) 3-COOCH BEHAR UTTAR (SC) WB-3 Cooch Behar Polytechnic 4-COOCH BEHAR DAKSHIN 6-SITAI (SC) WB-4 Dinhata College 7 DINHATA 8 NATABARI WB-5 Tufanganj Mahavidyalaya 9- TUFANGANJ 10-KUMARGRAM (ST) 11-KALCHINI (ST) WB-6 Alipurduar University 12-ALIPURDUAR 13-FALAKATA (SC) 14-MADARIHAT (ST) 15- DHUPGURI (SC) WB-7 NBU 2nd Campus, Science Building 17- JALPAIGURI (SC) WB-8 Netaji Subash Open University 16- MAYNAGURI (SC) 18- RAJGANJ (SC) WB-9 NBU 2nd Campus, Technology Building 19- DABGRAM FULBARI 20- MAL (ST) WB-10 Parimal Mitra Smriti College, Mal 21- NAGRAKATA (ST) The Scottish Universities’ Mission Institution (S.U.M.I.), WB-11 22 - KALIMPONG Kalimpong WB-12 Darjeeling Government College 23-DARJEELING WB-13 St. Alphonsus High School 24-KURSEONG 25-MATIGARA & NAXALBARI (SC) WB-14 Siliguri College 26-SILIGURI 27-PHANSIDEWA (ST) 28- CHOPRA 29- ISLAMPUR WB-15 Islampur College 30-GOALPOKHER 31- CHAKULIA 32-KARANDIGHI 33-HEMTABAD (SC) WB-16 Raiganj Polytechnic 34-KALIAGANJ (SC) 35-RAIGANJ AC 36-ITAHAR AC 37-KUSHMANDI (SC) WB-17 Buniadpur Mahavidyalaya 42-HARIRAMPUR 38-KUMARGANJ 39-BALURGHAT WB-18 Balurghat College 40-TAPAN(ST) 41-GANGARAMPUR(SC) 43-HABIBPUR (ST) 44-GAZOLE (SC) 48-RATUA WB-19 MALDA POLYTECHNIC COLLEGE 49-MANIKCHAK 53-SUJAPUR 54-BAISNABNAGAR Counting Name of the Counting Centre AC No. & Name Centre No. -

THE WEST BENGAL COLLEGE SERVICE COMMISSION Vacancy Status (Tentative) for the Posts of Assistant Professor in Government-Aided Colleges of West Bengal (Advt
THE WEST BENGAL COLLEGE SERVICE COMMISSION Vacancy Status (Tentative) for the Posts of Assistant Professor in Government-aided Colleges of West Bengal (Advt. No. 1/2018) English UR OBC-A OBC-B SC ST PWD 46 15 20 25 36 16 Sl No College University UR 1 Birsa Munda Memorial College 2 Gobinda Prasad Mahavidyalaya 3 Jamini Roy College BANKURA UNIVERSITY 4 Patrasayer Mahavidyalaya 5 Raipur Block Mahavidyalaya 6 Ramananda College. (Day+ Evening) 7 Kandra Radhakanta Kundu Mahavidyalaya 8 Memari College 9 Purbasthali College BURDWAN UNIVERSITY 10 Sailajananda Falguni Smriti Mahavidyalaya 11 Syamsundar College 12 Gokhale Memorial Girls' College 13 Naba Ballygunge Mahavidyalaya CALCUTTA UNIVERSITY 14 Rammohan College 15 Udaynarayanpur Madhabilata Mahavidyalaya 16 Baneswar Sarathibala Mahavidyalaya CPB UNIVERSITY 17 Tufangunj College 18 Balurghat College 19 Dewan Abdul Gani College 20 Dr. Meghnad Saha College GOUR BANGA UNIVERSITY 21 Harishchandrapur College 22 Malda College 23 Berhampur College 24 Domkal Girls' College KALYANI UNIVERSITY 25 Nagar College 26 Prof. Syed Nurul Hasan College 27 Deshbandhu Mahavidyalaya KAZI NAZRUL UNIVERSITY (ASANSOL) 28 Falakata College 29 Falakata College 30 Ghoshpukur College 31 Kalimpong College NORTH BENGAL UNIVERSITY 32 Nani Bhattacharya Smarak Mahavidyalaya 33 Rajganj College 34 Sukanta Mahavidyalaya 35 University B.T. and Evening College 36 Bikramjeet Goswami Memorial College 37 Chitta Mahato Memorial College SIDHO KANHO BIRSHA UNIVERSITY 38 Panchakot Mahavidyalaya 39 Belda College 40 Chaipat Saheed Pradyot -

THE WEST BENGAL COLLEGE SERVICE COMMISSION Vacancy Status (Tentative) for the Posts of Assistant Professor in Government-Aided Colleges of West Bengal (Advt
THE WEST BENGAL COLLEGE SERVICE COMMISSION Vacancy Status (Tentative) for the Posts of Assistant Professor in Government-aided Colleges of West Bengal (Advt. No. 1/2018) CHEMISTRY UR OBC-A OBC-B SC ST PWD 36 8 6 26 21 6 Sl No College University UR 1 Abhedananda Mahavidyalaya 2 Kalna College BURDWAN UNIVERSITY 3 Polba Mahavidyalaya 4 Rampurhat College 5 Gour Mohan Sachin Mandal Mahavidyalaya CALCUTTA UNIVERSITY 6 Coochbehar College CPB UNIVERSITY 7 Dinhata College 8 Kaliachak College GOUR BANGA UNIVERSITY 9 Malda College 10 Dukhulal Nibaran Chandra College 11 Dukhulal Nibaran Chandra College 12 Dumkal College 13 Krishnath College KALYANI UNIVERSITY 14 Santipur College 15 Srikrishna College 16 Sripat Singh College 17 Kulti College KAZI NAZRUL UNIVERSITY (ASANSOL) 18 Triveni Devi Bhalotia College 19 Alipurduar College 20 Ananda Chandra College 21 Kalimpong College NORTH BENGAL UNIVERSITY 22 Kurseong College 23 Parimal mitra smriti mahavidyalaya 24 Sukanta Mahavidyalaya 25 Manbhum Mahavidyalaya 26 Raghunathpur College SIDHO KANHO BIRSHA UNIVERSITY 27 Raghunathpur College 28 Belda College 29 Belda College 30 Kharagpur College VIDYASAGAR UNIVERSITY 31 Midnapore College 32 Panskura Banamali College 33 Silda Chandra Sekhar College 34 Gobardanga Hindu College 35 Mrinalini Datta Mahavidyapith WEST BENGAL STATE UNIVERSITY 36 Saheed Nurul Islam Mahavidyalaya Sl No College University OBC-A 1 Saldiha College BANKURA UNIVERSITY 2 Harimohan Ghosh College CALCUTTA UNIVERSITY 3 Ramsaday College 4 Krishnagar Women's College KALYANI UNIVERSITY 5 Alipurduar -

Sukanta Mondal CURRICULUM VITAE Assistant Professor in Chemistry Email: [email protected] Department of Education [email protected] A
Sukanta Mondal CURRICULUM VITAE Assistant Professor in Chemistry Email: [email protected] Department of Education [email protected] A. M. School of Educational Sciences Assam University (A Central University) Silchar 788011, Assam, India Web: sites.google.com/site/sukantamondalaus/ Experience Assistant Professor in Chemistry Oct. 2017 – till date Department of Education Assam, India A. M. School of Educational Sciences Assam University (A Central University), Silchar National Postdoctoral Fellow Feb. 2017 – Oct. 2017 Postdoctoral Research with Prof. Swapan K Pati Bengaluru, Karnataka Theoretical Sciences Unit Jawaharlal Nehru Centre for Advanced Scientific Research CTS Research Visitor Nov. 2016 Department of Chemistry & Center for Theoretical Studies Kharagpur, India Indian Institute of Technology Kharagpur Postdoctoral Research with Prof. Gabriel Merino Sept. 2015 – Aug. 2016 Departamento de Fisica Aplicada, CINVESTAV Merida Merida, Mexico Research Assistant Jun. – Jul. 2015 Department of Chemistry & Center for Theoretical Studies Kharagpur, India Indian Institute of Technology Kharagpur Education Ph.D., Indian Institute of Technology Kharagpur 2009 – 2015 Department of Chemistry Kharagpur, India Supervisor: Prof. P. K. Chattaraj Thesis: All-metal and nonmetal clusters and their gas storage potential M.Sc., University of Pune 2009 Centre for Advanced Studies in Chemistry Pune, India Department of Chemistry Supervisor: Prof. A. S. Kumbhar Project: Synthesis and characterization of different Cu(I) and Cu(II) Polypyridyl complexes B.Sc., University of Burdwan 2006 Department of Chemistry, Raghunathpur College, Purulia WB, India Page | 1 Journal Publications During Assistant Professorship: 1. G. G. Nnabuike, Sukanta Mondal, S. Salunke-Gawali, A. S. Patil, R. J. Butcher, J. A. Obaleye, “Structural features of nickel (II) mixed ligand complexes with mefenamic acid and nitrogen donor ligands” J.