Ballot Order Effect Is Huge: Evidence from Texas1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Kesha Rogers: Independent 'Classical' Candidate for Congress From
INTERVIEW Kesha Rogers: Independent ‘Classical’ Candidate for Congress from Texas’ 9th C.D. Oct. 23—In an interview today, less than two weeks before the November 6 Midterm elections, independent candidate Kesha Rogers stressed that her campaign is finding an absolute thirst for big ideas and the types of crash-program problem solving that is characteristic of the space pro- gram. Rogers, who is spearheading the LaRouche PAC’s Campaign to Secure the Future’s intervention into the Midterms, is running as an inde- pendent in Texas’ 9th C.D. against in- cumbent Democrat Al Green. Green positioned himself to lead the insane impeachment drive for the Democrats against Donald Trump in grandstanding Congressional speeches in 2017 and early 2018. In those speeches, Green proclaimed, contrary to the explicit words of the Constitution, that impeachment was Cartoons lampooning Rogers’ opponent, Democrat incumbent Greedy Al Green, who a matter of partisan whim, that the has introduced legislation to impeach President Trump. Multi-millionaire Green Constitution did not require that the presides over one of the poorest districts in Texas. President commit any crime to be im- peached. As a result, Green received a flood of dona- type of partisan and identity politics which have failed tions from Democratic organizations nationally, while us and turned statecraft into a small-minded spectator doing virtually nothing for his district, which is one of sport, resulting in whole sections of our population the poorest districts in Texas. being stuck in place, going nowhere, or far worse. Al The 9th C.D. was gerrymandered by former House Green presides over this district like an entitled slum Speaker Tom Delay to dump significant minority popu- lord, doling out small favors and small programs to lations into one district, in order to protect Republican make abject poverty somehow more comfortable. -

WHEREAS, Congressional Candidate Kesha Rogers Describes and Defines Herself As a Larouche Democrat, and WHEREAS, Ms. Rogers' C
WHEREAS, congressional candidate Kesha Rogers describes and defines herself as a LaRouche Democrat, and WHEREAS, Ms. Rogers’ campaign rhetoric, literature, platform positions and website confirm that she is a dedicated follower of Lyndon LaRouche and is an associate of and messenger for the LaRouche Movement, and WHEREAS, prior actions by Lyndon LaRouche and the LaRouche Movement include instances of illegal activities, discriminatory proclamations and thuggish behavior, and WHEREAS, the historical record of documentation, both produced by and relating to Lyndon LaRouche and the LaRouche Movement contains clear, convincing and overwhelming evidence of discrimination based on race, religion, sexual orientation and ethnic origin, and WHEREAS, the rules of the Texas Democratic Party (Art. I, B, 1.) require that no test of membership, nor oaths of loyalty, to the Texas Democratic Party shall be used if those oaths or tests would have the effect of requiring members of the Democratic Party to acquiesce in, condone or support discrimination based on race, religion, sexual orientation, and ethnic origin, now therefore be it RESOLVED, that no Rules or Declarations of the Texas Democratic Party that require support for Party nominees shall be enforced or have any application as they relate to the candidacy of any person identifying him or herself as aligned with the LaRouche Movement or Lyndon LaRouche, and, be it further RESOLVED, that Members, Officers and Candidates of the Texas Democratic Party are neither required nor encouraged to support -

Judge – Criminal District Court
NONPARTISAN ELECTION MATERIAL VOTERS GUIDE LEAGUE OF WOMEN VOTERS OF HOUSTON EDUCATION FUND NOVEMBER 6, 2018 • GENERAL ELECTION • POLLS OPEN 7AM TO 7PM INDEX THINGS VOTERS United States Senator . 5. SHOULD NOW United States Representative . .5 K PHOTO ID IS REQUIRED TO VOTE IN PERSON IN ALL TEXAS ELECTIONS Governor . .13 Those voting in person, whether voting early or on Election Day, will be required to present a photo Lieutenant Governor . .14 identification or an alternative identification allowed by law. Please see page 2 of this Voters Guide for additional information. Attorney General . 14. LWV/TEXAS EDUCATION FUND EARLY VOTING PROVIDES INFORMATION ON Comptroller of Public Accounts . 15. Early voting will begin on Monday, October 22 and end on Friday, November 2. See page 12 of this Voters CANDIDATES FOR U.S. SENATE Guide for locations and times. Any registered Harris County voter may cast an early ballot at any early voting Commissioner of General Land Office . .15 AND STATEWIDE CANDIDATES location in Harris County. Our thanks to our state organization, Commissioner of Agriculture . 16. the League of Women Voters of VOTING BY MAIL Texas, for contacting all opposed Railroad Commissioner . 16. Voters may cast mail ballots if they are at least 65 years old, if they will be out of Harris County during the candidates for U.S. Senator, Supreme Court . .17 Early Voting period and on Election Day, if they are sick or disabled or if they are incarcerated but eligible to Governor, Lieutenant Governor, vote. Mail ballots may be requested by visiting harrisvotes.com or by phoning 713-755-6965. -

Download Report
July 15th Campaign Finance Reports Covering January 1 – June 30, 2021 STATEWIDE OFFICEHOLDERS July 18, 2021 GOVERNOR – Governor Greg Abbott – Texans for Greg Abbott - listed: Contributions: $20,872,440.43 Expenditures: $3,123,072.88 Cash-on-Hand: $55,097,867.45 Debt: $0 LT. GOVERNOR – Texans for Dan Patrick listed: Contributions: $5,025,855.00 Expenditures: $827,206.29 Cash-on-Hand: $23,619,464.15 Debt: $0 ATTORNEY GENERAL – Attorney General Ken Paxton reported: Contributions: $1,819,468.91 Expenditures: $264,065.35 Cash-on-Hand: $6,839,399.65 Debt: $125,000.00 COMPTROLLER – Comptroller Glenn Hegar reported: Contributions: $853,050.00 Expenditures: $163,827.80 Cash-on-Hand: $8,567,261.96 Debt: $0 AGRICULTURE COMMISSIONER – Agriculture Commissioner Sid Miller listed: Contributions: $71,695.00 Expenditures: $110,228.00 Cash-on-Hand: $107,967.40 The information contained in this publication is the property of Texas Candidates and is considered confidential and may contain proprietary information. It is meant solely for the intended recipient. Access to this published information by anyone else is unauthorized unless Texas Candidates grants permission. If you are not the intended recipient, any disclosure, copying, distribution or any action taken or omitted in reliance on this is prohibited. The views expressed in this publication are, unless otherwise stated, those of the author and not those of Texas Candidates or its management. STATEWIDES Debt: $0 LAND COMMISSIONER – Land Commissioner George P. Bush reported: Contributions: $2,264,137.95 -

Vladimir Vernadsky's
st SCIENCE21 CENTURY & TECHNOLOGY SPRING 2013 www.21stcenturysciencetech.com $10.00 CELEBRATING Vladimir Vernadsky’s 150th Year Anniversary st SCIENCE21 CENTURY & TECHNOLOGY Vol. 26, No. 1 Spring 2013 Features News 150 YEARS OF VERNADSKY 4 NEWS BRIEFS Introduction 6 SPACE William Jones 66 Curiosity Discovers Mars Could V.I. Vernadsky and the Contemporary World Have Supported Life 8 Academician Erik Galimov Marsha Freeman 13 The Science of the Biosphere and Astrobiology 68 Strategic Defense of Earth: Academician M. Ya. Marov Unanswered Questions Kesha Rogers, Jason Ross, 16 The Vernadsky Strategy Benjamin Deniston Colonel Alexander A. Ignatenko GREAT PROJECTS 22 Biospheric Energy-Flux Density 73 NAWAPA Update: Economic Benjamin Deniston Development or ‘Back to Nature’? 42 A.I. Oparin: Fraud, Fallacy, or Both? VERNADSKY Meghan Rouillard 75 Russia and Ukraine Celebrate Vernadsky’s Anniversary 57 Getting the Dose-Response Wrong: A Costly Marsha Freeman Environmental Problem Edward J. Calabrese, Ph.D. Departments 2 EDITORIAL Jason Ross BOOKS 77 Search for the Ultimate Energy Source by Stephen O. Dean reviewed by Marsha Freeman 78 Maps of the Ancient Sea Kings: Evidence of Advanced Civilization in the Ice Age by Charles H. Hapgood reviewed by Charles Hughes On the Cover: Vladimir I. Vernadsky. Painting by A.E. Yeletsky, 1949, Vernadsky Institute of Geochemistry and Analytical Chemistry. st EDITORIAL SCIENCE21 CENTURY & TECHNOLOGY EDITORIAL STAFF Editor-in-Chief Vernadsky Was Not Jason Ross Managing Editor Marsha Freeman An Environmentalist Associate Editors Elijah C. Boyd s we celebrate the 150th birth- coming a mighty geological force. David Cherry Christine Craig day of the great scientist Vladi- There arises the problem of the recon- Liona Fan-Chiang Amir Vernadsky, it is of utmost struction of the biosphere in the inter- Colin M. -

The Evolution of the Digital Political Advertising Network
PLATFORMS AND OUTSIDERS IN PARTY NETWORKS: THE EVOLUTION OF THE DIGITAL POLITICAL ADVERTISING NETWORK Bridget Barrett A thesis submitted to the faculty at the University of North Carolina at Chapel Hill in partial fulfillment of the requirements for the degree of Master of Arts at the Hussman School of Journalism and Media. Chapel Hill 2020 Approved by: Daniel Kreiss Adam Saffer Adam Sheingate © 2020 Bridget Barrett ALL RIGHTS RESERVED ii ABSTRACT Bridget Barrett: Platforms and Outsiders in Party Networks: The Evolution of the Digital Political Advertising Network (Under the direction of Daniel Kreiss) Scholars seldom examine the companies that campaigns hire to run digital advertising. This thesis presents the first network analysis of relationships between federal political committees (n = 2,077) and the companies they hired for electoral digital political advertising services (n = 1,034) across 13 years (2003–2016) and three election cycles (2008, 2012, and 2016). The network expanded from 333 nodes in 2008 to 2,202 nodes in 2016. In 2012 and 2016, Facebook and Google had the highest normalized betweenness centrality (.34 and .27 in 2012 and .55 and .24 in 2016 respectively). Given their positions in the network, Facebook and Google should be considered consequential members of party networks. Of advertising agencies hired in the 2016 electoral cycle, 23% had no declared political specialization and were hired disproportionately by non-incumbents. The thesis argues their motivations may not be as well-aligned with party goals as those of established political professionals. iii TABLE OF CONTENTS LIST OF TABLES AND FIGURES .................................................................................................................... V POLITICAL CONSULTING AND PARTY NETWORKS ............................................................................... -

Crowdsourcing Applications of Voting Theory Daniel Hughart
Crowdsourcing Applications of Voting Theory Daniel Hughart 5/17/2013 Most large scale marketing campaigns which involve consumer participation through voting makes use of plurality voting. In this work, it is questioned whether firms may have incentive to utilize alternative voting systems. Through an analysis of voting criteria, as well as a series of voting systems themselves, it is suggested that though there are no necessarily superior voting systems there are likely enough benefits to alternative systems to encourage their use over plurality voting. Contents Introduction .................................................................................................................................... 3 Assumptions ............................................................................................................................... 6 Voting Criteria .............................................................................................................................. 10 Condorcet ................................................................................................................................. 11 Smith ......................................................................................................................................... 14 Condorcet Loser ........................................................................................................................ 15 Majority ................................................................................................................................... -

TEXAS MUNICIPAL COURTS EDUCATION CENTER FACULTY ROSTER Prosecutors Conference
TEXAS MUNICIPAL COURTS EDUCATION CENTER FACULTY ROSTER Prosecutors Conference Michael Acuña Mark Goodner Judge Deputy Counsel and Director of City of Dallas Judicial Education 2014 Main Street Suite 227 TMCEC Ned Minevitz Dallas, TX 75201 2210 Hancock Drive TxDOT Grant Administrator & 214.647.9934 Austin, TX 78756 Program Attorney [email protected] 512.320.8274 TMCEC [email protected] 2210 Hancock Drive Jaime Brew Austin, TX 78756 Court Administrator Ryan Henry 512.320.8274 130 Town Center Blvd Law Office of Ryan Henry [email protected] Coppell, TX 75019 Law Office of Ryan Henry 1380 972.301.3651 Pantheon Way, #110 David Newell [email protected] San Antonio, TX 78232 Judge 210.257.6357 Texas Court of Criminal Appeals Robby Chapman [email protected] 201 West 14th Street, Rom 106 Director of Clerk Education & Austin, TX 78701 Program Attorney Brian Holman 512.463.1551 TMCEC Presiding Judge [email protected] 2210 Hancock Drive Lewisville Austin, TX 78756 PO Box 299002 Ryan Kellus Turner [email protected] Lewisville, TX 75029 General Counsel & Director of 972.219.3419 Education Peter De Leef [email protected] TMCEC Associate Judge 2210 Hancock Drive City of El Lago Timothy Kirwin Austin, TX 78756 98 Lakeshore Drive Alternate Judge 512.320.8274 El Lago, TX 77586 City of Hedwig Village [email protected] 713.807.1100 955 Piney Point [email protected] Houston, TX 77024 281.657.2000 Chase Gomillion [email protected] Prosecutor City of Austin Adam Litchtenberger 700 E. 7th St. Prosecutor Austin, TX 78701 City of Austin 512.974.2586 700 E. -

TEXAS MUNICIPAL COURTS EDUCATION CENTER FACULTY ROSTER Prosecutors Conference
TEXAS MUNICIPAL COURTS EDUCATION CENTER FACULTY ROSTER Prosecutors Conference Michael Acuña Chase Gomillion Timothy Kirwin Judge Prosecutor Alternate Judge City of Dallas City of Austin City of Hedwig Village 2014 Main Street Suite 227 700 E. 7th St. 955 Piney Point Dallas, TX 75201 Austin, TX 78701 Houston, TX 77024 214.647.9934 512.974.2586 281.657.2000 [email protected] [email protected] [email protected] Jaime Brew Mark Goodner Adam Litchtenberger Court Administrator Deputy Counsel and Director of Prosecutor 130 Town Center Blvd Judicial Education City of Austin Coppell, TX 75019 TMCEC 700 E. 7th St. 972.301.3651 2210 Hancock Drive Austin, TX 78701 [email protected] Austin, TX 78756 512.974.4804 512.320.8274 [email protected] Cass Callaway [email protected] Presiding Judge Ned Minevitz Hutchins Ryan Henry TxDOT Grant Administrator & PO Box 500 Law Office of Ryan Henry Program Attorney Hutchins, TX 75141-0500 Law Office of Ryan Henry 1380 TMCEC 214.360.9787 Pantheon Way, #110 2210 Hancock Drive [email protected] San Antonio, TX 78232 Austin, TX 78756 210.257.6357 512.320.8274 Robby Chapman [email protected] [email protected] Director of Clerk Education & Program Attorney Brian Holman David Newell TMCEC Presiding Judge Judge 2210 Hancock Drive Lewisville Texas Court of Criminal Appeals Austin, TX 78756 PO Box 299002 201 West 14th Street, Rom 106 [email protected] Lewisville, TX 75029 Austin, TX 78701 972.219.3419 512.463.1551 Peter De Leef [email protected] [email protected] Associate Judge City of El Lago Ryan Kellus Turner 98 Lakeshore Drive General Counsel & Director of El Lago, TX 77586 Education 713.807.1100 TMCEC [email protected] 2210 Hancock Drive Austin, TX 78756 512.320.8274 [email protected] 2210 Hancock Drive Austin, Texas 78756 512.320.8274 800.252.3718 fax 512.435.6118 MICHAEL ACUÑA Michael Acuña received his J.D. -

Salsa2hjournal 1..24
HOUSE JOURNAL EIGHTY-SECOND LEGISLATURE, REGULAR SESSION PROCEEDINGS FIRST DAY Ð TUESDAY, JANUARY 11, 2011 In accordance with the laws and Constitution of the State of Texas, the members-elect of the house of representatives assembled this day in the hall of the house of representatives in the city of Austin at 12 noon. The Honorable Hope Andrade, secretary of state of the State of Texas, called the House of Representatives of the Eighty-Second Legislature of the State of Texas to order. The invocation was offered by Archbishop Daniel Nicholas Cardinal DiNardo of Galveston-Houston, as follows: Almighty and compassionate Lord, you have revealed your glory to all nations and have care for all. We humbly thank you for this land, our state, a land rich in resources but above all rich in its many people. May we be a people mindful of your love, justice, and kindness. Save us from violence, discord, and confusion, from pride and arrogance, and from every evil way. God of wisdom and justice, through you authority is rightly administered, laws are enacted, and judgement is decreed. Let the light of your divine wisdom direct the deliberations of this legislature and shine forth in all its proceedings and laws, framed for our rules and governance. May this house of representatives seek to preserve the common good and continue to bring us the blessings of liberty and equality. Assist with your spirit of council and fortitude the speaker and all the representatives, that their administration be conducted in good judgement and be eminently useful to the citizens of this state. -

Texas Fact Book
LEGISLATIVE BUDGET BOARD Texas Fact Book LEGISLATIVE BUDGET BOARD 2014 YELLOW (PMS 7403C): C5, M15, Y57 .25” BLEED ON ALL 4 SIDES Texas Fact Book LEGISLATIVE BUDGET BOARD 2014 LEGISLATIVE BUDGET BOARD EIGHTY-THIRD TEXAS LEGISLATURE DAVID DEWHURST, CO-CHAIR Lieutenant Governor, Austin JOE STRAUS, CO-CHAIR Representative District 121, San Antonio Speaker of the House of Representatives TOMMY WILLIAMS* Senatorial District 5, Th e Woodlands Chair, Senate Committee on Finance ROBERT DUNCAN Senatorial District 28, Lubbock JUAN “CHUY” HINOJOSA Senatorial District 20, McAllen JUDITH ZAFFIRINI Senatorial District 21, Laredo JIM PITTS Representative District 10, Waxahachie Chair, House Committee on Appropriations HARVEY HILDERBRAN Representative District 53, Kerrville Chair, House Committee on Ways and Means DAN BRANCH Representative District 108, Dallas SYLVESTER TURNER Representative District 139, Houston *Chairman Williams resigned from the Texas Senate on October 26, 2013 CONTENTS STATE GOVERNMENT Statewide Elected Officials.................................................................... 1 Members of the Eighty-third Texas Legislature ............................................ 3 The Senate ........................................................................................ 3 The House of Representatives .......................................................... 4 Senate Standing Committees................................................................ 9 House of Representatives Standing Committees.......................................11 -
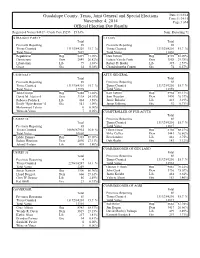
Gems Election Summary Report
Guadalupe County, Texas, Joint General and Special Elections Date:11/12/14 Time:11:34:15 November 4, 2014 Page:1 of 4 Official Election Day Results Registered Voters 84817 - Cards Cast 13253 15.63% Num. Reporting 71 STRAIGHT PARTY LT GOV Total Total Precincts Reporting 69 Precincts Reporting 69 Times Counted 13192/84201 15.7 % Times Counted 13192/84201 15.7 % Total Votes 7639 Total Votes 13056 Republican Rep 5497 71.96% Dan Patrick Rep 8759 67.09% Democratic Dem 2049 26.82% Leticia Van de Putte Dem 3888 29.78% Libertarian Lib 79 1.03% Robert D. Butler Lib 335 2.57% Green Gre 14 0.18% Chandrakantha Courtn Gre 74 0.57% US SENATE ATTY GENERAL Total Total Precincts Reporting 69 Precincts Reporting 69 Times Counted 13192/84201 15.7 % Times Counted 13192/84201 15.7 % Total Votes 12978 Total Votes 12959 John Cornyn Rep 9248 71.26% Ken Paxton Rep 8964 69.17% David M. Alameel Dem 3118 24.03% Sam Houston Dem 3490 26.93% Rebecca Paddock Lib 464 3.58% Jamie Balagia Lib 413 3.19% Emily "Spicybrown" S Gre 141 1.09% Jamar Osborne Gre 92 0.71% Mohammed Tahiro 0 0.00% Write-in Votes 7 0.05% COMPTROLLER OF PUB ACCTS Total US REP 15 Precincts Reporting 69 Total Times Counted 13192/84201 15.7 % Precincts Reporting 65 Total Votes 12817 Times Counted 10896/67954 16.0 % Glenn Hegar Rep 8750 68.27% Total Votes 10660 Mike Collier Dem 3443 26.86% Eddie Zamora Rep 7365 69.09% Ben Sanders Lib 481 3.75% Ruben Hinojosa Dem 2890 27.11% Deb Shafto Gre 143 1.12% Johnny Partain Lib 405 3.80% COMMISSIONER OF GEN LAND US REP 35 Total Total Precincts Reporting 69 Precincts Reporting 4 Times Counted 13192/84201 15.7 % Times Counted 2296/16247 14.1 % Total Votes 12932 Total Votes 2249 George P.