Complex Numbers and Complex Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Refresher Course Content
Calculus I Refresher Course Content 4. Exponential and Logarithmic Functions Section 4.1: Exponential Functions Section 4.2: Logarithmic Functions Section 4.3: Properties of Logarithms Section 4.4: Exponential and Logarithmic Equations Section 4.5: Exponential Growth and Decay; Modeling Data 5. Trigonometric Functions Section 5.1: Angles and Radian Measure Section 5.2: Right Triangle Trigonometry Section 5.3: Trigonometric Functions of Any Angle Section 5.4: Trigonometric Functions of Real Numbers; Periodic Functions Section 5.5: Graphs of Sine and Cosine Functions Section 5.6: Graphs of Other Trigonometric Functions Section 5.7: Inverse Trigonometric Functions Section 5.8: Applications of Trigonometric Functions 6. Analytic Trigonometry Section 6.1: Verifying Trigonometric Identities Section 6.2: Sum and Difference Formulas Section 6.3: Double-Angle, Power-Reducing, and Half-Angle Formulas Section 6.4: Product-to-Sum and Sum-to-Product Formulas Section 6.5: Trigonometric Equations 7. Additional Topics in Trigonometry Section 7.1: The Law of Sines Section 7.2: The Law of Cosines Section 7.3: Polar Coordinates Section 7.4: Graphs of Polar Equations Section 7.5: Complex Numbers in Polar Form; DeMoivre’s Theorem Section 7.6: Vectors Section 7.7: The Dot Product 8. Systems of Equations and Inequalities (partially included) Section 8.1: Systems of Linear Equations in Two Variables Section 8.2: Systems of Linear Equations in Three Variables Section 8.3: Partial Fractions Section 8.4: Systems of Nonlinear Equations in Two Variables Section 8.5: Systems of Inequalities Section 8.6: Linear Programming 10. Conic Sections and Analytic Geometry (partially included) Section 10.1: The Ellipse Section 10.2: The Hyperbola Section 10.3: The Parabola Section 10.4: Rotation of Axes Section 10.5: Parametric Equations Section 10.6: Conic Sections in Polar Coordinates 11. -
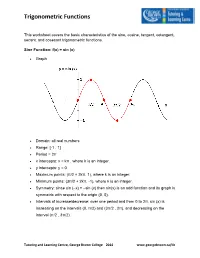
Trigonometric Functions
Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer. -

Lecture 5: Complex Logarithm and Trigonometric Functions
LECTURE 5: COMPLEX LOGARITHM AND TRIGONOMETRIC FUNCTIONS Let C∗ = C \{0}. Recall that exp : C → C∗ is surjective (onto), that is, given w ∈ C∗ with w = ρ(cos φ + i sin φ), ρ = |w|, φ = Arg w we have ez = w where z = ln ρ + iφ (ln stands for the real log) Since exponential is not injective (one one) it does not make sense to talk about the inverse of this function. However, we also know that exp : H → C∗ is bijective. So, what is the inverse of this function? Well, that is the logarithm. We start with a general definition Definition 1. For z ∈ C∗ we define log z = ln |z| + i argz. Here ln |z| stands for the real logarithm of |z|. Since argz = Argz + 2kπ, k ∈ Z it follows that log z is not well defined as a function (it is multivalued), which is something we find difficult to handle. It is time for another definition. Definition 2. For z ∈ C∗ the principal value of the logarithm is defined as Log z = ln |z| + i Argz. Thus the connection between the two definitions is Log z + 2kπ = log z for some k ∈ Z. Also note that Log : C∗ → H is well defined (now it is single valued). Remark: We have the following observations to make, (1) If z 6= 0 then eLog z = eln |z|+i Argz = z (What about Log (ez)?). (2) Suppose x is a positive real number then Log x = ln x + i Argx = ln x (for positive real numbers we do not get anything new). -

An Appreciation of Euler's Formula
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 1 Article 17 An Appreciation of Euler's Formula Caleb Larson North Dakota State University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Larson, Caleb (2017) "An Appreciation of Euler's Formula," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 1 , Article 17. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss1/17 Rose- Hulman Undergraduate Mathematics Journal an appreciation of euler's formula Caleb Larson a Volume 18, No. 1, Spring 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 [email protected] a scholar.rose-hulman.edu/rhumj North Dakota State University Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 1, Spring 2017 an appreciation of euler's formula Caleb Larson Abstract. For many mathematicians, a certain characteristic about an area of mathematics will lure him/her to study that area further. That characteristic might be an interesting conclusion, an intricate implication, or an appreciation of the impact that the area has upon mathematics. The particular area that we will be exploring is Euler's Formula, eix = cos x + i sin x, and as a result, Euler's Identity, eiπ + 1 = 0. Throughout this paper, we will develop an appreciation for Euler's Formula as it combines the seemingly unrelated exponential functions, imaginary numbers, and trigonometric functions into a single formula. To appreciate and further understand Euler's Formula, we will give attention to the individual aspects of the formula, and develop the necessary tools to prove it. -

Think Python
Think Python How to Think Like a Computer Scientist 2nd Edition, Version 2.2.18 Think Python How to Think Like a Computer Scientist 2nd Edition, Version 2.2.18 Allen Downey Green Tea Press Needham, Massachusetts Copyright © 2015 Allen Downey. Green Tea Press 9 Washburn Ave Needham MA 02492 Permission is granted to copy, distribute, and/or modify this document under the terms of the Creative Commons Attribution-NonCommercial 3.0 Unported License, which is available at http: //creativecommons.org/licenses/by-nc/3.0/. The original form of this book is LATEX source code. Compiling this LATEX source has the effect of gen- erating a device-independent representation of a textbook, which can be converted to other formats and printed. http://www.thinkpython2.com The LATEX source for this book is available from Preface The strange history of this book In January 1999 I was preparing to teach an introductory programming class in Java. I had taught it three times and I was getting frustrated. The failure rate in the class was too high and, even for students who succeeded, the overall level of achievement was too low. One of the problems I saw was the books. They were too big, with too much unnecessary detail about Java, and not enough high-level guidance about how to program. And they all suffered from the trap door effect: they would start out easy, proceed gradually, and then somewhere around Chapter 5 the bottom would fall out. The students would get too much new material, too fast, and I would spend the rest of the semester picking up the pieces. -

Natural Domain of a Function • Range Calculations Table of Contents (Continued)
~ THE UNIVERSITY OF AKRON w Mathematics and Computer Science calculus Article: Functions menu Directory • Table of Contents • Begin tutorial on Functions • Index Copyright c 1995{1998 D. P. Story Last Revision Date: 11/6/1998 Functions Table of Contents 1. Introduction 2. The Concept of a Function 2.1. Constructing Functions • The Use of Algebraic Expressions • Piecewise Definitions • Descriptive or Conceptual Methods 2.2. Evaluation Issues • Numerical Evaluation • Symbolic Evalulation 2.3. What's in a Name • The \Standard" Way • Functions Named by the Depen- dent Variable • Descriptive Naming • Famous Functions 2.4. Models for Functions • A Function as a Mapping • Venn Diagram of a Function • A Function as a Black Box 2.5. Calculating the Domain and Range • The Natural Domain of a Function • Range Calculations Table of Contents (continued) 2.6. Recognizing Functions • Interpreting the Terminology • The Vertical Line Test 3. Graphing: First Principles 4. Methods of Combining Functions 4.1. The Algebra of Functions 4.2. The Composition of Functions 4.3. Shifting and Rescaling • Horizontal Shifting • Vertical Shifting • Rescaling 5. Classification of Functions • Polynomial Functions • Rational Functions • Algebraic Functions 1. Introduction In the world of Mathematics one of the most common creatures en- countered is the function. It is important to understand the idea of a function if you want to gain a thorough understanding of Calculus. Science concerns itself with the discovery of physical or scientific truth. In a portion of these investigations, researchers (or engineers) attempt to discern relationships between physical quantities of interest. There are many ways of interpreting the meaning of the word \relation- ships," but in Calculus we are most often concerned with functional relationships. -

False Dilemma Wikipedia Contents
False dilemma Wikipedia Contents 1 False dilemma 1 1.1 Examples ............................................... 1 1.1.1 Morton's fork ......................................... 1 1.1.2 False choice .......................................... 2 1.1.3 Black-and-white thinking ................................... 2 1.2 See also ................................................ 2 1.3 References ............................................... 3 1.4 External links ............................................. 3 2 Affirmative action 4 2.1 Origins ................................................. 4 2.2 Women ................................................ 4 2.3 Quotas ................................................. 5 2.4 National approaches .......................................... 5 2.4.1 Africa ............................................ 5 2.4.2 Asia .............................................. 7 2.4.3 Europe ............................................ 8 2.4.4 North America ........................................ 10 2.4.5 Oceania ............................................ 11 2.4.6 South America ........................................ 11 2.5 International organizations ...................................... 11 2.5.1 United Nations ........................................ 12 2.6 Support ................................................ 12 2.6.1 Polls .............................................. 12 2.7 Criticism ............................................... 12 2.7.1 Mismatching ......................................... 13 2.8 See also -

Pivotal Decompositions of Functions
PIVOTAL DECOMPOSITIONS OF FUNCTIONS JEAN-LUC MARICHAL AND BRUNO TEHEUX Abstract. We extend the well-known Shannon decomposition of Boolean functions to more general classes of functions. Such decompositions, which we call pivotal decompositions, express the fact that every unary section of a function only depends upon its values at two given elements. Pivotal decom- positions appear to hold for various function classes, such as the class of lattice polynomial functions or the class of multilinear polynomial functions. We also define function classes characterized by pivotal decompositions and function classes characterized by their unary members and investigate links between these two concepts. 1. Introduction A remarkable (though immediate) property of Boolean functions is the so-called Shannon decomposition, or Shannon expansion (see [20]), also called pivotal decom- position [2]. This property states that, for every Boolean function f : {0, 1}n → {0, 1} and every k ∈ [n]= {1,...,n}, the following decomposition formula holds: 1 0 n (1) f(x) = xk f(xk)+ xk f(xk) , x = (x1,...,xn) ∈{0, 1} , a where xk = 1 − xk and xk is the n-tuple whose i-th coordinate is a, if i = k, and xi, otherwise. Here the ‘+’ sign represents the classical addition for real numbers. Decomposition formula (1) means that we can precompute the function values for xk = 0 and xk = 1 and then select the appropriate value depending on the value of xk. By analogy with the cofactor expansion formula for determinants, here 1 0 f(xk) (resp. f(xk)) is called the cofactor of xk (resp. xk) for f and is derived by setting xk = 1 (resp. -

Functional C
Functional C Pieter Hartel Henk Muller January 3, 1999 i Functional C Pieter Hartel Henk Muller University of Southampton University of Bristol Revision: 6.7 ii To Marijke Pieter To my family and other sources of inspiration Henk Revision: 6.7 c 1995,1996 Pieter Hartel & Henk Muller, all rights reserved. Preface The Computer Science Departments of many universities teach a functional lan- guage as the first programming language. Using a functional language with its high level of abstraction helps to emphasize the principles of programming. Func- tional programming is only one of the paradigms with which a student should be acquainted. Imperative, Concurrent, Object-Oriented, and Logic programming are also important. Depending on the problem to be solved, one of the paradigms will be chosen as the most natural paradigm for that problem. This book is the course material to teach a second paradigm: imperative pro- gramming, using C as the programming language. The book has been written so that it builds on the knowledge that the students have acquired during their first course on functional programming, using SML. The prerequisite of this book is that the principles of programming are already understood; this book does not specifically aim to teach `problem solving' or `programming'. This book aims to: ¡ Familiarise the reader with imperative programming as another way of imple- menting programs. The aim is to preserve the programming style, that is, the programmer thinks functionally while implementing an imperative pro- gram. ¡ Provide understanding of the differences between functional and imperative pro- gramming. Functional programming is a high level activity. -

Notes on Functional Programming with Haskell
Notes on Functional Programming with Haskell H. Conrad Cunningham [email protected] Multiparadigm Software Architecture Group Department of Computer and Information Science University of Mississippi 201 Weir Hall University, Mississippi 38677 USA Fall Semester 2014 Copyright c 1994, 1995, 1997, 2003, 2007, 2010, 2014 by H. Conrad Cunningham Permission to copy and use this document for educational or research purposes of a non-commercial nature is hereby granted provided that this copyright notice is retained on all copies. All other rights are reserved by the author. H. Conrad Cunningham, D.Sc. Professor and Chair Department of Computer and Information Science University of Mississippi 201 Weir Hall University, Mississippi 38677 USA [email protected] PREFACE TO 1995 EDITION I wrote this set of lecture notes for use in the course Functional Programming (CSCI 555) that I teach in the Department of Computer and Information Science at the Uni- versity of Mississippi. The course is open to advanced undergraduates and beginning graduate students. The first version of these notes were written as a part of my preparation for the fall semester 1993 offering of the course. This version reflects some restructuring and revision done for the fall 1994 offering of the course|or after completion of the class. For these classes, I used the following resources: Textbook { Richard Bird and Philip Wadler. Introduction to Functional Program- ming, Prentice Hall International, 1988 [2]. These notes more or less cover the material from chapters 1 through 6 plus selected material from chapters 7 through 9. Software { Gofer interpreter version 2.30 (2.28 in 1993) written by Mark P. -

Using Differentials to Differentiate Trigonometric and Exponential Functions Tevian Dray
Using Differentials to Differentiate Trigonometric and Exponential Functions Tevian Dray Tevian Dray ([email protected]) received his B.S. in mathematics from MIT in 1976, his Ph.D. in mathematics from Berkeley in 1981, spent several years as a physics postdoc, and is now a professor of mathematics at Oregon State University. A Fellow of the American Physical Society for his early work in general relativity, his current research interests include the octonions as well as science education. He directs the Vector Calculus Bridge Project. (http://www.math.oregonstate.edu/bridge) Differentiating a polynomial is easy. To differentiate u2 with respect to u, start by computing d.u2/ D .u C du/2 − u2 D 2u du C du2; and then dropping the last term, an operation that can be justified in terms of limits. Differential notation, in general, can be regarded as a shorthand for a formal limit argument. Still more informally, one can argue that du is small compared to u, so that the last term can be ignored at the level of approximation needed. After dropping du2 and dividing by du, one obtains the derivative, namely d.u2/=du D 2u. Even if one regards this process as merely a heuristic procedure, it is a good one, as it always gives the correct answer for a polynomial. (Physicists are particularly good at knowing what approximations are appropriate in a given physical context. A physicist might describe du as being much smaller than the scale imposed by the physical situation, but not so small that quantum mechanics matters.) However, this procedure does not suffice for trigonometric functions. -

Leonhard Euler - Wikipedia, the Free Encyclopedia Page 1 of 14
Leonhard Euler - Wikipedia, the free encyclopedia Page 1 of 14 Leonhard Euler From Wikipedia, the free encyclopedia Leonhard Euler ( German pronunciation: [l]; English Leonhard Euler approximation, "Oiler" [1] 15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.[2] He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy. Euler spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He is considered to be the preeminent mathematician of the 18th century, and one of the greatest of all time. He is also one of the most prolific mathematicians ever; his collected works fill 60–80 quarto volumes. [3] A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is our teacher in all things," which has also been translated as "Read Portrait by Emanuel Handmann 1756(?) Euler, read Euler, he is the master of us all." [4] Born 15 April 1707 Euler was featured on the sixth series of the Swiss 10- Basel, Switzerland franc banknote and on numerous Swiss, German, and Died Russian postage stamps. The asteroid 2002 Euler was 18 September 1783 (aged 76) named in his honor. He is also commemorated by the [OS: 7 September 1783] Lutheran Church on their Calendar of Saints on 24 St. Petersburg, Russia May – he was a devout Christian (and believer in Residence Prussia, Russia biblical inerrancy) who wrote apologetics and argued Switzerland [5] forcefully against the prominent atheists of his time.