Numerical Methods
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Fast and Efficient Algorithms for Evaluating Uniform and Nonuniform
World Academy of Science, Engineering and Technology International Journal of Computer and Information Engineering Vol:13, No:8, 2019 Fast and Efficient Algorithms for Evaluating Uniform and Nonuniform Lagrange and Newton Curves Taweechai Nuntawisuttiwong, Natasha Dejdumrong Abstract—Newton-Lagrange Interpolations are widely used in quadratic computation time, which is slower than the others. numerical analysis. However, it requires a quadratic computational However, there are some curves in CAGD, Wang-Ball, DP time for their constructions. In computer aided geometric design and Dejdumrong curves with linear complexity. In order to (CAGD), there are some polynomial curves: Wang-Ball, DP and Dejdumrong curves, which have linear time complexity algorithms. reduce their computational time, Bezier´ curve is converted Thus, the computational time for Newton-Lagrange Interpolations into any of Wang-Ball, DP and Dejdumrong curves. Hence, can be reduced by applying the algorithms of Wang-Ball, DP and the computational time for Newton-Lagrange interpolations Dejdumrong curves. In order to use Wang-Ball, DP and Dejdumrong can be reduced by converting them into Wang-Ball, DP and algorithms, first, it is necessary to convert Newton-Lagrange Dejdumrong algorithms. Thus, it is necessary to investigate polynomials into Wang-Ball, DP or Dejdumrong polynomials. In this work, the algorithms for converting from both uniform and the conversion from Newton-Lagrange interpolation into non-uniform Newton-Lagrange polynomials into Wang-Ball, DP and the curves with linear complexity, Wang-Ball, DP and Dejdumrong polynomials are investigated. Thus, the computational Dejdumrong curves. An application of this work is to modify time for representing Newton-Lagrange polynomials can be reduced sketched image in CAD application with the computational into linear complexity. -

Mials P
Euclid's Algorithm 171 Euclid's Algorithm Horner’s method is a special case of Euclid's Algorithm which constructs, for given polyno- mials p and h =6 0, (unique) polynomials q and r with deg r<deg h so that p = hq + r: For variety, here is a nonstandard discussion of this algorithm, in terms of elimination. Assume that d h(t)=a0 + a1t + ···+ adt ;ad =06 ; and n p(t)=b0 + b1t + ···+ bnt : Then we seek a polynomial n−d q(t)=c0 + c1t + ···+ cn−dt for which r := p − hq has degree <d. This amounts to the square upper triangular linear system adc0 + ad−1c1 + ···+ a0cd = bd adc1 + ad−1c2 + ···+ a0cd+1 = bd+1 . adcn−d−1 + ad−1cn−d = bn−1 adcn−d = bn for the unknown coefficients c0;:::;cn−d which can be uniquely solved by back substitution since its diagonal entries all equal ad =0.6 19aug02 c 2002 Carl de Boor 172 18. Index Rough index for these notes 1-1:-5,2,8,40 cartesian product: 2 1-norm: 79 Cauchy(-Bunyakovski-Schwarz) 2-norm: 79 Inequality: 69 A-invariance: 125 Cauchy-Binet formula: -9, 166 A-invariant: 113 Cayley-Hamilton Theorem: 133 absolute value: 167 CBS Inequality: 69 absolutely homogeneous: 70, 79 Chaikin algorithm: 139 additive: 20 chain rule: 153 adjugate: 164 change of basis: -6 affine: 151 characteristic function: 7 affine combination: 148, 150 characteristic polynomial: -8, 130, 132, 134 affine hull: 150 circulant: 140 affine map: 149 codimension: 50, 53 affine polynomial: 152 coefficient vector: 21 affine space: 149 cofactor: 163 affinely independent: 151 column map: -6, 23 agrees with y at Λt:59 column space: 29 algebraic dual: 95 column -

CS321-001 Introduction to Numerical Methods
CS321-001 Introduction to Numerical Methods Lecture 3 Interpolation and Numerical Differentiation Professor Jun Zhang Department of Computer Science University of Kentucky Lexington, KY 40506-0633 Polynomial Interpolation Given a set of discrete values, how can we estimate other values between these data The method that we will use is called polynomial interpolation. We assume the data we had are from the evaluation of a smooth function. We may be able to use a polynomial p(x) to approximate this function, at least locally. A condition: the polynomial p(x) takes the given values at the given points (nodes), i.e., p(xi) = yi with 0 ≤ i ≤ n. The polynomial is said to interpolate the table, since we do not know the function. 2 Polynomial Interpolation Note that all the points are passed through by the curve 3 Polynomial Interpolation We do not know the original function, the interpolation may not be accurate 4 Order of Interpolating Polynomial A polynomial of degree 0, a constant function, interpolates one set of data If we have two sets of data, we can have an interpolating polynomial of degree 1, a linear function x x1 x x0 p(x) y0 y1 x0 x1 x1 x0 y1 y0 y0 (x x0 ) x1 x0 Review carefully if the interpolation condition is satisfied Interpolating polynomials can be written in several forms, the most well known ones are the Lagrange form and Newton form. Each has some advantages 5 Lagrange Form For a set of fixed nodes x0, x1, …, xn, the cardinal functions, l0, l1,…, ln, are defined as 0 if i j li (x j ) ij -

Lagrange & Newton Interpolation
Lagrange & Newton interpolation In this section, we shall study the polynomial interpolation in the form of Lagrange and Newton. Given a se- quence of (n +1) data points and a function f, the aim is to determine an n-th degree polynomial which interpol- ates f at these points. We shall resort to the notion of divided differences. Interpolation Given (n+1) points {(x0, y0), (x1, y1), …, (xn, yn)}, the points defined by (xi)0≤i≤n are called points of interpolation. The points defined by (yi)0≤i≤n are the values of interpolation. To interpolate a function f, the values of interpolation are defined as follows: yi = f(xi), i = 0, …, n. Lagrange interpolation polynomial The purpose here is to determine the unique polynomial of degree n, Pn which verifies Pn(xi) = f(xi), i = 0, …, n. The polynomial which meets this equality is Lagrange interpolation polynomial n Pnx=∑ l j x f x j j=0 where the lj ’s are polynomials of degree n forming a basis of Pn n x−xi x−x0 x−x j−1 x−x j 1 x−xn l j x= ∏ = ⋯ ⋯ i=0,i≠ j x j −xi x j−x0 x j−x j−1 x j−x j1 x j−xn Properties of Lagrange interpolation polynomial and Lagrange basis They are the lj polynomials which verify the following property: l x = = 1 i= j , ∀ i=0,...,n. j i ji {0 i≠ j They form a basis of the vector space Pn of polynomials of degree at most equal to n n ∑ j l j x=0 j=0 By setting: x = xi, we obtain: n n ∑ j l j xi =∑ j ji=0 ⇒ i =0 j=0 j=0 The set (lj)0≤j≤n is linearly independent and consists of n + 1 vectors. -

Mathematical Topics
A Mathematical Topics This chapter discusses most of the mathematical background needed for a thor ough understanding of the material presented in the book. It has been mentioned in the Preface, however, that math concepts which are only used once (such as the mediation operator and points vs. vectors) are discussed right where they are introduced. Do not worry too much about your difficulties in mathematics, I can assure you that mine a.re still greater. - Albert Einstein. A.I Fourier Transforms Our curves are functions of an arbitrary parameter t. For functions used in science and engineering, time is often the parameter (or the independent variable). We, therefore, say that a function g( t) is represented in the time domain. Since a typical function oscillates, we can think of it as being similar to a wave and we may try to represent it as a wave (or as a combination of waves). When this is done, we have the function G(f), where f stands for the frequency of the wave, and we say that the function is represented in the frequency domain. This turns out to be a useful concept, since many operations on functions are easy to carry out in the frequency domain. Transforming a function between the time and frequency domains is easy when the function is periodic, but it can also be done for certain non periodic functions. The present discussion is restricted to periodic functions. 1IIIt Definition: A function g( t) is periodic if (and only if) there exists a constant P such that g(t+P) = g(t) for all values of t (Figure A.la). -

A Low‐Cost Solution to Motion Tracking Using an Array of Sonar Sensors and An
A Low‐cost Solution to Motion Tracking Using an Array of Sonar Sensors and an Inertial Measurement Unit A thesis presented to the faculty of the Russ College of Engineering and Technology of Ohio University In partial fulfillment of the requirements for the degree Master of Science Jason S. Maxwell August 2009 © 2009 Jason S. Maxwell. All Rights Reserved. 2 This thesis titled A Low‐cost Solution to Motion Tracking Using an Array of Sonar Sensors and an Inertial Measurement Unit by JASON S. MAXWELL has been approved for the School of Electrical Engineering Computer Science and the Russ College of Engineering and Technology by Maarten Uijt de Haag Associate Professor School of Electrical Engineering and Computer Science Dennis Irwin Dean, Russ College of Engineering and Technology 3 ABSTRACT MAXWELL, JASON S., M.S., August 2009, Electrical Engineering A Low‐cost Solution to Motion Tracking Using an Array of Sonar Sensors and an Inertial Measurement Unit (91 pp.) Director of Thesis: Maarten Uijt de Haag As the desire and need for unmanned aerial vehicles (UAV) increases, so to do the navigation and system demands for the vehicles. While there are a multitude of systems currently offering solutions, each also possess inherent problems. The Global Positioning System (GPS), for instance, is potentially unable to meet the demands of vehicles that operate indoors, in heavy foliage, or in urban canyons, due to the lack of signal strength. Laser‐based systems have proven to be rather costly, and can potentially fail in areas in which the surface absorbs light, and in urban environments with glass or mirrored surfaces. -

The AMATYC Review, Fall 1992-Spring 1993. INSTITUTION American Mathematical Association of Two-Year Colleges
DOCUMENT RESUME ED 354 956 JC 930 126 AUTHOR Cohen, Don, Ed.; Browne, Joseph, Ed. TITLE The AMATYC Review, Fall 1992-Spring 1993. INSTITUTION American Mathematical Association of Two-Year Colleges. REPORT NO ISSN-0740-8404 PUB DATE 93 NOTE 203p. AVAILABLE FROMAMATYC Treasurer, State Technical Institute at Memphis, 5983 Macon Cove, Memphis, TN 38134 (for libraries 2 issues free with $25 annual membership). PUB TYPE Collected Works Serials (022) JOURNAL CIT AMATYC Review; v14 n1-2 Fall 1992-Spr 1993 EDRS PRICE MF01/PC09 Plus Postage. DESCRIPTORS *College Mathematics; Community Colleges; Computer Simulation; Functions (Mathematics); Linear Programing; *Mathematical Applications; *Mathematical Concepts; Mathematical Formulas; *Mathematics Instruction; Mathematics Teachers; Technical Mathematics; Two Year Colleges ABSTRACT Designed as an avenue of communication for mathematics educators concerned with the views, ideas, and experiences of two-year collage students and teachers, this journal contains articles on mathematics expoition and education,as well as regular features presenting book and software reviews and math problems. The first of two issues of volume 14 contains the following major articles: "Technology in the Mathematics Classroom," by Mike Davidson; "Reflections on Arithmetic-Progression Factorials," by William E. Rosentl,e1; "The Investigation of Tangent Polynomials with a Computer Algebra System," by John H. Mathews and Russell W. Howell; "On Finding the General Term of a Sequence Using Lagrange Interpolation," by Sheldon Gordon and Robert Decker; "The Floating Leaf Problem," by Richard L. Francis; "Approximations to the Hypergeometric Distribution," by Chltra Gunawardena and K. L. D. Gunawardena; aid "Generating 'JE(3)' with Some Elementary Applications," by John J. Edgeli, Jr. The second issue contains: "Strategies for Making Mathematics Work for Minorities," by Beverly J. -
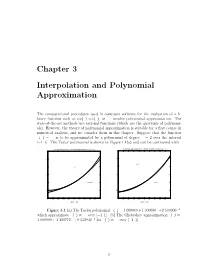
Chapter 3 Interpolation and Polynomial Approximation
Chapter 3 Interpolation and Polynomial Approximation The computational procedures used in computer software for the evaluation of a li- brary function such as sin(x); cos(x), or ex, involve polynomial approximation. The state-of-the-art methods use rational functions (which are the quotients of polynomi- als). However, the theory of polynomial approximation is suitable for a first course in numerical analysis, and we consider them in this chapter. Suppose that the function f(x) = ex is to be approximated by a polynomial of degree n = 2 over the interval [¡1; 1]. The Taylor polynomial is shown in Figure 1.1(a) and can be contrasted with 2 x The Taylor polynomial p(x)=1+x+0.5x2 which approximates f(x)=ex over [−1,1] The Chebyshev approximation q(x)=1+1.129772x+0.532042x for f(x)=e over [−1,1] 3 3 2.5 2.5 y=ex 2 2 y=ex 1.5 1.5 2 1 y=1+x+0.5x 1 y=q(x) 0.5 0.5 0 0 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Figure 1.1(a) Figure 1.1(b) Figure 3.1 (a) The Taylor polynomial p(x) = 1:000000+ 1:000000x +0:500000x2 which approximate f(x) = ex over [¡1; 1]. (b) The Chebyshev approximation q(x) = 1:000000 + 1:129772x + 0:532042x2 for f(x) = ex over [¡1; 1]. -

Anl-7826 Chinese Remainder Ind Interpolation
ANL-7826 CHINESE REMAINDER IND INTERPOLATION ALGORITHMS John D. Lipson UolC-AUA-USAEC- ARGONNE NATIONAL LABORATORY, ARGONNE, ILLINOIS Prepared for the U.S. ATOMIC ENERGY COMMISSION under contract W-31-109-Eng-38 The facilities of Argonne National Laboratory are owned by the United States Govern ment. Under the terms of a contract (W-31 -109-Eng-38) between the U. S. Atomic Energy 1 Commission. Argonne Universities Association and The University of Chicago, the University employs the staff and operates the Laboratory in accordance with policies and programs formu lated, approved and reviewed by the Association. MEMBERS OF ARGONNE UNIVERSITIES ASSOCIATION The University of Arizona Kansas State University The Ohio State University Carnegie-Mellon University The University of Kansas Ohio University Case Western Reserve University Loyola University The Pennsylvania State University The University of Chicago Marquette University Purdue University University of Cincinnati Michigan State University Saint Louis University Illinois Institute of Technology The University of Michigan Southern Illinois University University of Illinois University of Minnesota The University of Texas at Austin Indiana University University of Missouri Washington University Iowa State University Northwestern University Wayne State University The University of Iowa University of Notre Dame The University of Wisconsin NOTICE This report was prepared as an account of work sponsored by the United States Government. Neither the United States nor the United States Atomic Energy Commission, nor any of their employees, nor any of their contractors, subcontrac tors, or their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately-owned rights. -

Mathematics for IT Engineers
Mathematics for IT Engineers Pál Burai Copyright c 2019 Pál Burai UNIVERSITY OF DEBRECEN WWW.UNIDEB.HU Licensed under the Creative Commons Attribution-NonCommercial 3.0 Unported License (the “License”). You may not use this file except in compliance with the License. You may obtain a copy of the License at http://creativecommons.org/licenses/by-nc/3.0. Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an “AS IS” BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License. This work was supported by the construction EFOP-3.4.3-16-2016-00021. The project was sup- ported by the European Union, co-financed by the European Social Fund. Contents 1 Complex numbers .............................................5 1.1 A possible motivation introducing complex numbers5 1.2 Operations with complex numbers in algebraic form6 1.2.1 Algebraic form, real part, imaginary part..............................6 1.2.2 Graphical representation of complex numbers on the complex plane.......7 1.2.3 Addition of complex numbers in algebraic form........................8 1.2.4 Multiplication of complex numbers in algebraic form.....................9 1.2.5 Conjugate of complex numbers.................................... 12 1.3 Polar form and exponential form of complex numbers 13 1.3.1 Length and angle of complex numbers.............................. 13 1.3.2 Calculation with complex numbers in polar form....................... 18 1.3.3 Euler’s formula.................................................. 26 1.3.4 Calculation with complex numbers in exponential form................ -

Math 375: Lecture Notes
Math 375: Lecture notes Professor Monika Nitsche September 21, 2011 Contents 1 MATLAB Basics 8 1.1 Example:Plottingafunction . ... 8 1.2 Scripts....................................... 9 1.3 Settingupvectors................................ 10 1.4 VectorandMatrixoperations . 11 1.5 Plotting ...................................... 14 1.6 Printingdata ................................... 15 1.7 Forloops...................................... 15 1.8 Whileloops .................................... 16 1.9 Timingcode.................................... 17 1.10Functions ..................................... 17 2 Computing Fundamentals 20 2.1 Vectorizing, timing, operation counts, memory allocation........... 20 2.1.1 Vectorizing for legibility and speed . 20 1 2.1.2 Memoryallocation ............................ 21 2.1.3 Counting operations: Horner’s algorithm . 21 2.1.4 Counting operations: evaluating series . 22 2.2 Machine Representation of real numbers, Roundoff errors . ......... 23 2.2.1 Decimal and binary representation of reals . ..... 23 2.2.2 Floating point representation of reals . ..... 24 2.2.3 Machine precision, IEEE rounding, roundoff error . ...... 25 2.2.4 Loss of significant digits during subtraction . 27 2.3 Approximating derivatives, Taylor’s Theorem, plotting y = hp ........ 29 2.4 Big-ONotation .................................. 30 3 Solving nonlinear equations f(x) = 0 31 3.1 Bisection method to solve f(x)=0( 1.1).................... 32 § 3.2 Fixed point iteration to solve x = g(x) (FPI, 1.2)............... 34 § 3.2.1 Examples ................................. 34 3.2.2 TheFPI.................................. 34 3.2.3 ImplementingFPIinMatlab. 35 3.2.4 TheoreticalResults ............................ 35 3.2.5 Definitions................................. 37 3.2.6 Stoppingcriterion. 37 3.3 Newton’s method to solve f(x)=0( 1.4) ................... 38 § 3.3.1 Thealgorithm............................... 38 3.3.2 Matlabimplementation. 38 2 3.3.3 Theoreticalresults ............................ 39 3.4 Secant method ( 1.5).............................. -

Piecewise Polynomial Taylor Expansions – the Generalization of Fa`A Di Bruno's Formula
Takustr. 7 Zuse Institute Berlin 14195 Berlin Germany TOM STREUBEL1,CAREN TISCHENDORF,ANDREAS GRIEWANK2 Piecewise Polynomial Taylor Expansions – The Generalization of Faa` di Bruno’s Formula 1 0000-0003-4917-7977 2 0000-0001-9839-1473 ZIB Report 18-24 (May 2018) Zuse Institute Berlin Takustr. 7 14195 Berlin Germany Telephone: +49 30-84185-0 Telefax: +49 30-84185-125 E-mail: [email protected] URL: http://www.zib.de ZIB-Report (Print) ISSN 1438-0064 ZIB-Report (Internet) ISSN 2192-7782 Piecewise Polynomial Taylor Expansions – The Generalization of Faa` di Bruno’s Formula Tom Streubel and Caren Tischendorf and Andreas Griewank Abstract We present an extension of Taylor’s theorem towards nonsmooth evalua- tion procedures incorporating absolute value operaions. Evaluations procedures are computer programs of mathematical functions in closed form expression and al- low a different treatment of smooth operations and calls to the absolute value value function. The well known classical Theorem of Taylor defines polynomial approx- imation of sufficiently smooth functions and is widely used for the derivation and analysis of numerical integrators for systems of ordinary differential or differential algebraic equations, for the construction of solvers for the continuous nonlinear op- timization of finite dimensional objective functions and for root solving of nonlinear systems of equations. The herein provided proof is construtive and allow efficiently designed algorithms for the execution and computation of generalized piecewise polynomial expansions.