DOCSLIB.ORG

Lunar and Planetary Science XXX 1504.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lunar and Planetary Science XXX 1504.Pdf Lunar and Planetary Science XXX 1504.pdf DELIVERY OF METEOROIDS FROM 6 HEBE VIA YARKOVSKY THERMAL DRAG. W. F. Bottke, Jr., CRSR, Cornell University, Ithaca NY 14853-6801, USA, [email protected],D.P.Rubincam,NASA Goddard Space Flight Center, Greenbelt MD 20771, USA,J.A.Burns,CRSR, Cornell University, Ithaca NY 14853-6801, USA. Introduction after 9 Myr of integration (i.e., just before some particles hai =2:401 0:03 Yarkovsky thermal drag is a radiation effect which can begin to fall into the 6 resonance), AU, 3 1 da=dti 2:7 10 modify the semimajor axes of objects between 0.1 m to 10 a h drift rate of AU Myr . km in the main belt [1, 2]. It occurs when solar radiation is absorbed by a body orbiting the Sun. The absorbed light Single Case heats the body, but a delay takes place before the energy is An representative example of our results is provided by re-radiated. When this energy departs, it provides a small Fig. 1, which shows a meteoroid evolving under the combined ``kick'' to the body which can modify its orbit. The diurnal influence of the seasonal and diurnal Yarkovsky effects, col- component of this force is dependent on the body's spin lisions, distant perturbations, and planetary close encounters. rate and longitudinal temperature distribution. It causes the The open circles show the 9 spin axis reorientation events pro- body to spiral outward for prograde rotations and inward for duced over 42.32 Myr. The starting z -component for the spin b retrograde rotations. The ``seasonal'' component of this force axis ( z ) is -.790, which causes the object to evolve inward is dependent on the body's mean motion around the Sun and under the predominant influence of the diurnal Yarkovsky b ;b y its latitudinal temperature distribution. It causes the body to effect. The first spin axis change modifies x , but leaves b spiral inward, It is important to note that these forces have been the z strongly negative, such that evolution continues inward, empirically verified, and have already been used to explain though at a slightly faster rate. All this time, secular pertur- the orbital motion of the LAGEOS artificial satellite. bations continue to grow stronger, increasing the amplitude of e Yarkovsky thermal drag can be used to understand the the forced component as the object draws closer to the 6 res- delivery of meteoroids from the main belt to the Earth. Moti- onance. Then, at 12.20 Myr, the meteoroid, whose perihelion vation for this project comes from the fact that most meteorite is low enough to cross Mars's orbit, undergoes an encounter cosmic ray exposure (CRE) ages are 10-100 times longer than with Mars. This gravitational ``kick'' causes the meteoroid's the most probable dynamical paths carrying these bodies from a to increase, which pushing the object slightly outward. Since ^ resonant main belt orbits to the Earth [3]. Thus, meteoroids b hasn't changed, however, the inward drift continues at the have to reside in the main belt for millions of years before same rate for another 0.33 Myr. Then, at 12.53 Myr, another b spin axis re-orientation event occurs, giving z a strongly pos- reaching the 3:1 or 6 resonances. Since Yarkovsky thermal drag works over just the right timescales to explain both stony itive value (0.868). This causes the meteoroid to slow spiral and iron meteorite CRE ages, we believe it is the leading outward under the diurnal Yarkovsky effect. Enduring a few candidate to solve this problem. more Mars encounters (and a kicks), the body evolves away e from the 6 resonance, reducing the forced amplitude all the Meteoroids from 6 Hebe way back to its starting value. Finally, at 25.74 Myr, another Our formulation of the diurnal and seasonal Yarkovsky collision gets the meteoroid moving inward again. Several drag accelerations, and their inclusion into the symplectic b more spin axis flips occur, but they result in z values which integration routine ``swift-rmvs3'', was discussed last year are either strongly negative (diurnal drag dominates) or near 40 [4]. We now apply the code to study the evolution of 50 zero (seasonal drag dominates). Eventually, after Myr, R =1m e meteoroids evolving from asteroid 6 Hebe, a 200 km the object drifts deeply into the 6 resonance, causing its =2:425 S-type asteroid with osculating orbital elements a values to get pumped up to an Earth-crossing value. At this =0:169 i =15:05 AU, e ,and . Note that this places Hebe point, the code records the data and ends the run. a 0:084 close enough to the 6 resonance ( ) that its We can use Fig. 1 to make a few interesting observations. ejecta has a relatively high probability of being perturbed First of all, the 6 resonance does not appear to have a onto chaotic orbits which quickly become Earth-crossing. sharp boundary. Particles spiraling inward see their forced e Our simulations included perturbations from planets Venus amplitudes increase to Mars-crossing values well before the through Neptune. Each meteoroid was tracked for 50 Myr cross the nominal 6 boundary. Second, encounters with Mars of integration time. Thermal and material properties were before entering deeply into the 6 resonance are common, chosen to be consistent S class asteroids with porous or dusty though it only appears to delay the inward evolution of the surfaces. Each meteoroid was started with a random spin axis meteoroid's by a few Myr at best. Third, we find that only orientation; collisions were included to ``flip'' their spin axis the particles that survive long enough to pass deeply into the e from time to time. 6 resonance undergo large jumps. By the time this occurs, The maximum seasonal and diurnal da=dt rates for our many of the bodies have already reached Earth-crossing orbits. 3 1 2 1 10 2 10 meteoroids were AU Myr and 1 AU Myr . Since the diurnal drift rate is larger than the Evolution of Distribution seasonal drift rate, particles move inward and outward in a. Snapshots from the orbital evolution of all our Hebe-like a; e Collisions and the non-negligible seasonal drift rate, however, meteoroids in space are shown in Fig. 2. Solid lines ai cause h for the distribution to drift inward. For example, show the approximate values needed to reach Mars-crossing Lunar and Planetary Science XXX 1504.pdf YARKOVSKY THERMAL DRAG: W. F. Bottke et al. orbits, Earth-crossing orbits, the 3:1 resonance, and the 6 resonance, the latter assuming the meteoroids have a mean i 2.4 14 15 between - . Frame 2a and 2b show the meteoroids after 1 Myr and 2 Myr of evolution. Note how the Yarkovsky effect is causing the bodies to spread in a, while secular 2.35 υ Approximate 6 boundary perturbations are spreading the objects in e. After 5 Myr of evolution (Frame 2c), the bodies are now spread over a large Collision / Spin axis change part of the inner main belt. After 10 Myr of evolution (Frame 2.3 0 10203040 2d), one object has entered the 6 resonance, while a different object can be seen on a Mars-crossing orbit. Actually, at this time in the integration, at least 15 bodies (30%) have achieved 0.6 Mars-crossing orbits, though none have yet been removed from their main belt orbits. After 20 Myr of evolution (Frame 0.4 2e), objects can now be seen in the 3:1 resonance, the 6 resonance, and on Mars-crossing orbits. At this point, 9 0.2 particles have reached Earth-crossing orbits and have been removed from the run. The last frame shows the meteoroid distribution at the end of the integration (50 Myr). Only 17 0 0 10203040 particles remain, with two more working their way into the 6 resonance. In terms of overall statistical results, we found that 44 Figure 1: Evolution of single meteoroid from 6 Hebe. Note of the meteoroids became Mars-crossers (88%), while 34 how spin axis changes can change the sign of da=dt, and how became Earth-crossers (68%). The shortest interval needed encounters with Mars both push the object away from the 6 for a particle to reach a crossing orbit with Mars and Earth resonance and pull it inwards. was 5.53 Myr and 10.88 Myr, respectively. The median planet-crossing times for meteoroids with Mars and Earth were 11.92 Myr and 23.33 Myr, respectively. Note that most particles become Mars-crossing before well before they cross the derived ``boundary'' for the 6 resonance, implying the boundary itself is difficult to qualify. A related trend, though not readily apparent from Fig. 2, is that the meteoroids' forced e amplitude grows as the distribution nears the 6 resonance. (a) (b) This gives the overall distribution an almost triangular shape, with the point of the triangle near the 3:1 resonance and the base of the triangle near the 6 resonance. Finally, some bodies appear to reach Mars-crossing orbits well away from the 3:1 or 6 resonances; we suspect that higher-order mean-motion resonances with Mars are the cause. Conclusions (i) Delivery times of Hebe-like meteoroids to Earth- crossing orbits are consistent with stony meteorite CRE ages (c) (d) of tens of Myrs. (ii) Mars plays a bigger role in the evolution of material into the 6 resonance than previously thought. (iii) The 6 resonance is an efficient means of delivering material to Earth-crossing orbits.
Load more

Recommended publications
  • The Hamburg Meteorite Fall: Fireball Trajectory, Orbit and Dynamics
    The Hamburg Meteorite Fall: Fireball trajectory, orbit and dynamics P.G. Brown1,2*, D. Vida3, D.E. Moser4, M. Granvik5,6, W.J. Koshak7, D. Chu8, J. Steckloff9,10, A. Licata11, S. Hariri12, J. Mason13, M. Mazur3, W. Cooke14, and Z. Krzeminski1 *Corresponding author email: [email protected] ORCID ID: https://orcid.org/0000-0001-6130-7039 1Department of Physics and Astronomy, University of Western Ontario, London, Ontario, N6A 3K7, Canada 2Centre for Planetary Science and Exploration, University of Western Ontario, London, Ontario, N6A 5B7, Canada 3Department of Earth Sciences, University of Western Ontario, London, Ontario, N6A 3K7, Canada ( 4Jacobs Space Exploration Group, EV44/Meteoroid Environment Office, NASA Marshall Space Flight Center, Huntsville, AL 35812 USA 5Department of Physics, P.O. Box 64, 00014 University of Helsinki, Finland 6 Division of Space Technology, Luleå University of Technology, Kiruna, Box 848, S-98128, Sweden 7NASA Marshall Space Flight Center, ST11, Robert Cramer Research Hall, 320 Sparkman Drive, Huntsville, AL 35805, USA 8Chesapeake Aerospace LLC, Grasonville, MD 21638, USA 9Planetary Science Institute, Tucson, AZ, USA 10Department of Aerospace Engineering and Engineering Mechanics, University of Texas at Austin, Austin, TX, USA 11Farmington Community Stargazers, Farmington Hills, MI, USA 12Department of Physics and Astronomy, Eastern Michigan University, Ypsilanti, MI, USA 13Orchard Ridge Campus, Oakland Community College, Farmington Hills, MI, USA 14NASA Meteoroid Environment Office, Marshall Space Flight Center, Huntsville, Alabama 35812, USA Accepted to Meteoritics and Planetary Science, June 19, 2019 85 pages, 4 tables, 15 figures, 1 appendix. Original submission September, 2018. 1 Abstract The Hamburg (H4) meteorite fell on January 17, 2018 at 01:08 UT approximately 10km North of Ann Arbor, Michigan.
    [Show full text]
  • Lunar Occultations 2021
    Milky Way, Whiteside, MO July 7, 2018 References: http://www.seasky.org/astronomy/astronomy-calendar-2021.html http://www.asteroidoccultation.com/2021-BestEvents.htm https://in-the-sky.org/newscalyear.php?year=2021&maxdiff=7 https://www.go-astronomy.com/solar-system/event-calendar.htm https://www.photopills.com/articles/astronomical-events-photography- guide#step1 https://www.timeanddate.com/eclipse/ All Photos by Mark Jones Unless noted Southern Cross May 6, 2018 Tulum, MX Full Moon Events 2021 Largest Apr 27 2021: diameter: 33.7’; 345,572km May 26, 2021: diameter: 33.4’; 358,014km; Eclipse Smallest Oct 20, 2021: diameter: 29.7’; 402,517km; Eclipse Image below shows the apparent size difference between largest and smallest dates Canon DSLR FL=300mm Full Moon Events 2021 May 26 – Lunar Eclipse- partial from STL Partial Start 4:23am, Alt=9 deg moon set 5:43am, 80% covered Aug 22 - Blue Moon Nov 19 – Lunar Eclipse – Almost total from STL Partial Start 1:19am, Alt=61 deg Max Partial 3:05am, Alt=42 deg Partial End 4:49am, Alt=23 deg Total Lunar Eclipse, Oct 8 2014 Canon DSLR, Celestron C-8 Other Moon Events 2021 V Lunar-X on the Moon (Start Times) • Mar 20 – 16:01 Alt=54° • May 18 – 17:34 Alt=65° • Jul 16 – 17:00 Alt=42° • Sep 13 – 16:09 Alt=15° X • Nov 11 – 18:03 Alt=32° Lunar V also seen at same Sun angles Yellow=Favorable Moon Conditions Other Moon Events 2021 Lunar V - Visible at the same time just north of the X.
    [Show full text]
  • Hydrated Minerals on Asteroids: the Astronomical Record
    Hydrated Minerals on Asteroids: The Astronomical Record A. S. Rivkin, E. S. Howell, F. Vilas, and L. A. Lebofsky March 28, 2002 Corresponding Author: Andrew Rivkin MIT 54-418 77 Massachusetts Ave. Cambridge MA, 02139 [email protected] 1 1 Abstract Knowledge of the hydrated mineral inventory on the asteroids is important for deducing the origin of Earth’s water, interpreting the meteorite record, and unraveling the processes occurring during the earliest times in solar system history. Reflectance spectroscopy shows absorption features in both the 0.6-0.8 and 2.5-3.5 pm regions, which are diagnostic of or associated with hydrated minerals. Observations in those regions show that hydrated minerals are common in the mid-asteroid belt, and can be found in unex- pected spectral groupings, as well. Asteroid groups formerly associated with mineralogies assumed to have high temperature formation, such as MAand E-class asteroids, have been observed to have hydration features in their reflectance spectra. Some asteroids have apparently been heated to several hundred degrees Celsius, enough to destroy some fraction of their phyllosili- cates. Others have rotational variation suggesting that heating was uneven. We summarize this work, and present the astronomical evidence for water- and hydroxyl-bearing minerals on asteroids. 2 Introduction Extraterrestrial water and water-bearing minerals are of great importance both for understanding the formation and evolution of the solar system and for supporting future human activities in space. The presence of water is thought to be one of the necessary conditions for the formation of life as 2 we know it.
    [Show full text]
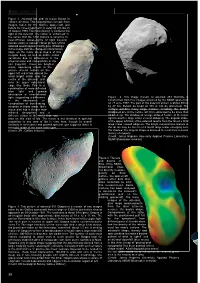
  • Iso and Asteroids
    r bulletin 108 Figure 1. Asteroid Ida and its moon Dactyl in enhanced colour. This colour picture is made from images taken by the Galileo spacecraft just before its closest approach to asteroid 243 Ida on 28 August 1993. The moon Dactyl is visible to the right of the asteroid. The colour is ‘enhanced’ in the sense that the CCD camera is sensitive to near-infrared wavelengths of light beyond human vision; a ‘natural’ colour picture of this asteroid would appear mostly grey. Shadings in the image indicate changes in illumination angle on the many steep slopes of this irregular body, as well as subtle colour variations due to differences in the physical state and composition of the soil (regolith). There are brighter areas, appearing bluish in the picture, around craters on the upper left end of Ida, around the small bright crater near the centre of the asteroid, and near the upper right-hand edge (the limb). This is a combination of more reflected blue light and greater absorption of near-infrared light, suggesting a difference Figure 2. This image mosaic of asteroid 253 Mathilde is in the abundance or constructed from four images acquired by the NEAR spacecraft composition of iron-bearing on 27 June 1997. The part of the asteroid shown is about 59 km minerals in these areas. Ida’s by 47 km. Details as small as 380 m can be discerned. The moon also has a deeper near- surface exhibits many large craters, including the deeply infrared absorption and a shadowed one at the centre, which is estimated to be more than different colour in the violet than any 10 km deep.
    [Show full text]
  • 3D Shape of Asteroid (6) Hebe from VLT/SPHERE Imaging: Implications for the Origin of Ordinary H Chondrites?
    A&A 604, A64 (2017) Astronomy DOI: 10.1051/0004-6361/201731021 & c ESO 2017 Astrophysics 3D shape of asteroid (6) Hebe from VLT/SPHERE imaging: Implications for the origin of ordinary H chondrites? M. Marsset1, B. Carry2; 3, C. Dumas4, J. Hanuš5, M. Viikinkoski6, P. Vernazza7, T. G. Müller8, M. Delbo2, E. Jehin9, M. Gillon9, J. Grice2; 10, B. Yang11, T. Fusco7; 12, J. Berthier3, S. Sonnett13, F. Kugel14, J. Caron14, and R. Behrend14 1 Astrophysics Research Centre, Queen’s University Belfast, BT7 1NN, UK e-mail: [email protected] 2 Université Côte d’Azur, Observatoire de la Côte d’Azur, 06304 Lagrange, CNRS, France 3 IMCCE, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ Paris 06, Univ. Lille, France 4 TMT Observatory, 100 W. Walnut Street, Suite 300, Pasadena, CA 91124, USA 5 Astronomical Institute, Faculty of Mathematics and Physics, Charles University, V Holešovickáchˇ 2, 18000 Prague, Czech Republic 6 Department of Mathematics, Tampere University of Technology, PO Box 553, 33101 Tampere, Finland 7 Aix Marseille Univ, CNRS, LAM, Laboratoire d’Astrophysique de Marseille, 13013 Marseille, France 8 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse, 85748 Garching, Germany 9 Space sciences, Technologies and Astrophysics Research Institute, Université de Liège, Allée du 6 Août 17, 4000 Liège, Belgium 10 Open University, School of Physical Sciences, The Open University, MK7 6AA, UK 11 European Southern Observatory (ESO), Alonso de Córdova 3107, 1900 Casilla Vitacura, Santiago, Chile 12 ONERA – the French Aerospace Lab, 92322 Châtillon, France 13 Planetary Science Institute, 1700 East Fort Lowell, Suite 106, Tucson, AZ 85719, USA 14 CdR & CdL Group: Lightcurves of Minor Planets and Variable Stars, Observatoire de Genève, 1290 Sauverny, Switzerland Received 22 April 2017 / Accepted 19 May 2017 ABSTRACT Context.
    [Show full text]
  • Thermal Evolution Models of Asteroids 559
    McSween et al.: Thermal Evolution Models of Asteroids 559 Thermal Evolution Models of Asteroids Harry Y. McSween Jr. University of Tennessee Amitabha Ghosh University of Tennessee Robert E. Grimm Blackhawk Geoservices Lionel Wilson Lancaster University Edward D. Young University of California at Los Angeles Thermal evolution models for asteroids that experienced metamorphism (ordinary chon- drites), aqueous alteration (carbonaceous chondrites), and melting and differentiation (HED achondrites) are compared. These models, based on decay of 26Al, can be used to study a va- riety of asteroidal processes such as the insulating effect of regolith, the buffering effect of ice and fluid flow, and the complications arising from redistribution of heat sources during differ- entiation. Thermal models can also account for an apparent relationship between peak tem- perature and heliocentric distance of asteroids in the main belt. Thermal evolution models using other heat sources (electromagnetic induction, collisions) are poorly constrained at this point and have been used primarily for simple plausibility calculations. 1. INTRODUCTION (LaTourrette and Wasserburg, 1997; Ghosh and McSween, 1998). This heat source appears capable of explaining the Many asteroids and the meteorites derived from them full range of temperature excursions of asteroids within the have been heated, as manifested in metamorphism, aque- main belt (Grimm and McSween, 1993). Although nebular ous alteration, melting, and differentiation. Almost half a heterogeneity of 26Al has
    [Show full text]
  • The Family of Asteroid (6) Hebe: Initial Results
    50th Lunar and Planetary Science Conference 2019 (LPI Contrib. No. 2132) 1047.pdf THE FAMILY OF ASTEROID (6) HEBE: INITIAL RESULTS. S. K. Fieber-Beyer1,2 and M. J. Gaffey,1,2 1Dept. of Space Studies, Box 9008, Univ. of North Dakota, Grand Forks, ND 58202. 2Visiting astronomer at the IRTF under contract from the NASA, which is operated by the Univ. of Hawai’i Mauna Kea, HI 97620. sherry- [email protected] Introduction: Focusing on asteroids identified as If this small group is part of a Hebe genetic family, strong meteorite sources based on dynamical criteria then logic implies that there should be Hebe-derived [1-3], led to the identification of asteroid (6) Hebe, objects nearer Hebe itself, which is the focus of the located near the intersection of the 3:1 and ѵ6 reso- proposed research effort. If this hypothesis cannot be nances, as the probable parent body of an abundant verified and there are no H-chondrite bodies on the meteorite type. Based on spectral data, [4] identified short side of the gap, then the alternate scenario would Hebe as an H-type chondrite. [Based on isotopic and suggest that the asteroids located on the far side of the chemical criteria, meteorite investigators have con- gap condensed from the same nebular compositional cluded that the ordinary chondrite groups (the abun- reservoir inferring several H-chondrite parents, a con- dant H, L, LL and the rarer HH, H/L & L/LL types) clusion which is at odds with the meteorite isotope each derive from a single original parent body.] The data, which point to a single H-chondrite parent body Portales Valley meteorite [5-7] and subsequent dynam- [26].
    [Show full text]
  • Hydrated Minerals on Asteroids 235
    Rivkin et al.: Hydrated Minerals on Asteroids 235 Hydrated Minerals on Asteroids: The Astronomical Record A. S. Rivkin Massachusetts Institute of Technology E. S. Howell Arecibo Observatory F. Vilas NASA Johnson Space Center L. A. Lebofsky University of Arizona Knowledge of the hydrated mineral inventory on the asteroids is important for deducing the origin of Earth’s water, interpreting the meteorite record, and unraveling the processes occurring during the earliest times in solar system history. Reflectance spectroscopy shows absorption features in both the 0.6–0.8 and 2.5–3.5-µm regions, which are diagnostic of or associated with hydrated minerals. Observations in those regions show that hydrated minerals are common in the mid-asteroid belt, and can be found in unexpected spectral groupings as well. Asteroid groups formerly associated with mineralogies assumed to have high-temperature formation, such as M- and E-class asteroids, have been observed to have hydration features in their reflectance spectra. Some asteroids have apparently been heated to several hundred degrees Celsius, enough to destroy some fraction of their phyllosilicates. Others have rotational variation suggesting that heating was uneven. We summarize this work, and present the astronomical evidence for water- and hydroxyl-bearing minerals on asteroids. 1. INTRODUCTION to be common. Indeed, water is found throughout the outer solar system on satellites (Clark and McCord, 1980; Clark Extraterrestrial water and water-bearing minerals are of et al., 1984), Kuiper Belt Objects (KBOs) (Brown et al., great importance both for understanding the formation and 1997), and comets (Bregman et al., 1988; Brooke et al., 1989) evolution of the solar system and for supporting future as ice, and on the planets as vapor (Larson et al., 1975; human activities in space.
    [Show full text]
  • SPIRE Measurements of Calibration Stars and Asteroids
    350μm SPIRE Observaons of Asteroids and Stars 25-27/03/2013 1 Photometer Rou+ne Calibra+on Programme Main Elements: • Observe Neptune and Uranus wHen visible • Observe Gamma Dra every .me pHotometer is used • Observe dark sky every .me pHotometer is used • Observe 2-3 stars per week • Observe 2-3 asteroids per week On a less frequent basis • Load curves of planets and brigHt asteroids • PHase ups • JFET noise tests • BSM calibraon cHeck 25-27/03/2013 2 Photometer Rou+ne Calibra+on "PHotometer 18 16 14 12 10 Cal % of SPIRE Time 8 6 4 2 0 82 81 80 79 78 77 76 75 74 73 72 71 70 69 68 67 66 65 64 63 62 61 60 59 58 57 56 55 54 53 52 51 50 49 Cycle Number 25-27/03/2013 3 Stars • Before launcH 8 stars selected with very good models • SPIRE observaons include these 8 stars plus some addi.onal stars taken from a secondary list establisHed before launcH • It was quickly establisHed that small map mode sHould be the default mode for making rou.ne observaons • Typically 4 scans were taken with eacH observaon taking about 6 minutes • 16 stars were observed in total: – One star, Delta Dra was too faint to Have a reliable detec.on so was dropped aer one observaon – Gamma Dra is always visible so was observed almost every pHotometer pair of days - but it is relavely faint • About 280 observaons made over rou.ne pHase 25-27/03/2013 4 Stars Star No. Obsrvaons Star No.
    [Show full text]
  • Asteroids: Their Composition and Impact Threat
    Bulletin of the Czech Geological Survey, Vol. 77, No. 4, 243–252, 2002 © Czech Geological Survey, ISSN 1210-3527 Asteroids: Their composition and impact threat THOMAS H. BURBINE Department of Mineral Sciences, National Museum of Natural History, Smithsonian Institution, Washington, DC 20560-0119, USA; e-mail: [email protected] Abstract. Impacts by near-Earth asteroids are serious threats to life as we know it. The energy of the impact will be a function of the mass of the asteroid and its impact velocity. The mass of an asteroid is very difficult to determine from Earth. One way to derive a near-Earth object’s mass is by estimating the object’s density from its surface composition. Reflectance spectra are the best way to determine an object’s composition since many minerals (e.g. olivine, pyroxene, hydrated silicates) have characteristic absorption features. However, metallic iron does not have characteristic ab- sorption bands and is very hard to identify from Earth. For a particular size, asteroids with compositions similar to iron meteorites pose the biggest impact threat since they have the highest densities, but they are expected to be only a few percent of the impacting population. Knowing an asteroid’s composition is also vital for understanding how best to divert an incoming asteroid. Key words: Earth, asteroids, impact features, meteorites, mineral composition, geologic hazards Introduction Impact threat As we enter a new millennium, we are constantly being I will first briefly review what we know about the num- bombarded with news of close encounters with near-Earth ber of near-Earth objects and the energy and effects of im- objects (NEOs).
    [Show full text]
  • Asteroid Masses and Improvement with Gaia
    A&A 472, 1017–1027 (2007) Astronomy DOI: 10.1051/0004-6361:20077479 & c ESO 2007 Astrophysics Asteroid masses and improvement with Gaia S. Mouret1,D.Hestroffer1, and F. Mignard2 1 IMCCE, UMR CNRS 8028, Paris observatory, 77 Av. Denfert-Rochereau, 75014 Paris, France e-mail: [mouret;hestroffer]@imcce.fr 2 OCA/Cassiopée, UMR CNRS 6062, Nice observatory, Le Mont Gros, BP 4229, 06304 Nice Cedex 4, France e-mail: [email protected] Received 14 March 2007 / Accepted 18 May 2007 ABSTRACT Context. The ESA astrometric mission Gaia, due for launch in late 2011, will observe a very large number of asteroids (∼350 000 brighter than V = 20) with an unprecedented positional precision (at the sub-milliarcsecond level). Aims. Gaia will yield masses of the hundred largest asteroids from gravitational perturbations during close approaches with target asteroids. The objective is to develop a global method to obtain these masses which will use simultaneously all perturbers together with their target asteroids. In this paper, we outline the numerical and statistical methodology and show how to estimate the accuracy. Methods. The method that we use is the variance analysis from the formulation of observed minus calculated position (O−C). We as- sume a linear relationship between the (O−C) and the fitted parameters which are the initial position and velocity of the asteroids and the masses of perturbers. The matrix giving the partial derivatives with respect to the positions and masses is computed by numerical integration of the variational equations. Results. We show that with Gaia it will be possible to derive more than 100 masses of minor planets 42 of which with a precision better than 10%.
    [Show full text]
  • Interesting Objects Near (6) Hebe. S. K. Fieber-Beyer1,2 1Dept. of Space Studies, Box 9008, Univ. North Dakota, Grand Forks, ND 58202
    52nd Lunar and Planetary Science Conference 2021 (LPI Contrib. No. 2548) 1233.pdf Interesting Objects Near (6) Hebe. S. K. Fieber-Beyer1,2 1Dept. of Space Studies, Box 9008, Univ. North Dakota, Grand Forks, ND 58202. 2Visitiing Astronomer at the IRTF under contract from the NASA, which is operated by the Univ. of Hawaii Mauna Kea, HI 97620. [email protected] Introduction: The Kirkwood Gaps are severely depleted zones in the asteroid belt located at proper motion resonances with Jupiter. The secular resonances are orbital resonances between two bodies with synchronized precessional frequencies, which helps to move objects in/out of the resonances. For example, objects near either of these resonances are subjected to excited eccentricities (e) and repeated planetary encounters, which ultimately remove asteroids and asteroidal fragments from these resonances. As such, theoretical models indicate the majority of main belt material delivered to the inner solar system, particularly to the Earth, originates from the 3:1 Kirkwood Gap and the ν6 secular resonance [1-8]. Changes in (e), (i), and (a) due to gravitational encounters with planets, as well as non-gravitational forces such as collisions with other asteroids and Yarkovsky effects can deliver nearby meter-kilometers scale objects into the chaotic zones of Figure 1: Spectra of the 1-μm absorption band asteroids discussed in this paper. The spectra were normalized the 3:1 Kirkwood Gap and the ν6 secular resonance [9- 18]. These objects are rapidly transferred to Earth- and and offset for clarity. Mars-crossing orbits making these particular resonances perfect hunting grounds for the source of meteorites and NEAs [19-23].
    [Show full text]