A Service-Points-Elo System for Beating the Tennis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
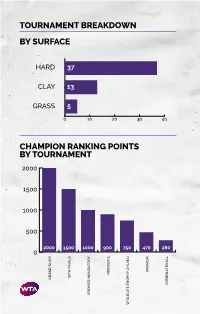
Tournament Breakdown by Surface Champion Ranking Points By
TOURNAMENT BREAKDOWN BY SURFACE HAR 37 CLAY 13 GRASS 5 0 10 20 30 40 CHAMPION RANKING POINTS BY TOURNAMENT 2000 1500 1000 500 2000 1500 1000 900 750 470 280 0 PREMIER PREMIER TA FINALS TA GRAN SLAM INTERNATIONAL PREMIER MANATORY TA ELITE TROPHY HUHAI TROPHY ELITE TA 55 WTA TOURNAMENTS BY REGION BY COUNTRY 8 CHINA 2 SPAIN 1 MOROCCO UNITED STATES 2 SWITZERLAND 7 OF AMERICA 1 NETHERLANDS 3 AUSTRALIA 1 AUSTRIA 1 NEW ZEALAND 3 GREAT BRITAIN 1 COLOMBIA 1 QATAR 3 RUSSIA 1 CZECH REPUBLIC 1 ROMANIA 2 CANADA 1 FRANCE 1 THAILAND 2 GERMANY 1 HONG KONG 1 TURKEY UNITED ARAB 2 ITALY 1 HUNGARY 1 EMIRATES 2 JAPAN 1 SOUTH KOREA 1 UZBEKISTAN 2 MEXICO 1 LUXEMBOURG TOURNAMENTS TOURNAMENTS International Tennis Federation As the world governing body of tennis, the Davis Cup by BNP Paribas and women’s Fed Cup by International Tennis Federation (ITF) is responsible for BNP Paribas are the largest annual international team every level of the sport including the regulation of competitions in sport and most prized in the ITF’s rules and the future development of the game. Based event portfolio. Both have a rich history and have in London, the ITF currently has 210 member nations consistently attracted the best players from each and six regional associations, which administer the passing generation. Further information is available at game in their respective areas, in close consultation www.daviscup.com and www.fedcup.com. with the ITF. The Olympic and Paralympic Tennis Events are also an The ITF is committed to promoting tennis around the important part of the ITF’s responsibilities, with the world and encouraging as many people as possible to 2020 events being held in Tokyo. -

Copy of DRAFT 2015 ATP Calendar As of 06
2015 Season Week Week Starting City Current Tournament Name Surface 1 Jan 5 Brisbane Brisbane International presented by Suncorp H Chennai Aircel Chennai Open H Doha Qatar ExxonMobil Open H 2 Jan 12 Auckland Heineken Open H Sydney Apia International Sydney H 3Jan 19 Melbourne Australian Open* H 4 5 Feb 2 Montpellier Open Sud de France IH Viña del Mar Royal Guard Open Chile CL Zagreb PBZ Zagreb Indoors IH 6 Feb 9 Rotterdam ABN AMRO World Tennis Tournament IH Memphis U.S. National Indoor Tennis Championships IH Buenos Aires/São Paulo -- TBD 7 Feb 16 Rio de Janiero Rio Open presented by Claro hdtv CL Delray Beach Delray Beach Open by The Venetian® Las Vegas H Marseille Open 13 IH 8 Feb 23 Acapulco Abierto Mexicano Telcel H Dubai Dubai Duty Free Tennis Championships H Buenos Aires/São Paulo -- TBD 9 Mar 2 10 Mar 9 Indian Wells BNP Paribas Open H 11 12 Mar 23 Miami Sony Open Tennis H 13 14Apr 6 Casablanca Grand Prix Hassan II CL Houston Fayez Sarofim & Co. US Men’s Clay Court Championship CL 15 Apr 13 Monte-Carlo Monte-Carlo Rolex Masters CL 16 Apr 20 Barcelona Barcelona Open BancSabadell CL Bucharest BRD Nastase Tiriac Trophy CL 17 Apr 27 Munich BMW Open CL Oeiras Portugal Open CL TBD 18 May 4 Madrid Mutua Madrid Open CL 19 May 11 Rome Internazionali BNL d’Italia CL 20 May 18 Düsseldorf Düsseldorf Open CL Nice Open de Nice Côte d’Azur CL 21May 25 Paris Roland Garros* CL 22 23 Jun 8 ’s-Hertogenbosch Topshelf Open G Stuttgart MercedesCup G 24 Jun 15 Halle Gerry Weber Open G London Aegon Championships G 25 Jun 22 Nottingham Aegon 250 G 26Jun 29 London Wimbledon* G 27 28 Jul 13 Newport Hall of Fame Tennis Championships G 29 Jul 20 Båstad SkiStar Swedish Open CL Bogota Claro Open Colombia H Umag Vegeta Croatia Open Umag CL 30 Jul 27 Hamburg bet-at-home Open CL Atlanta BB&T Atlanta Open H Gstaad Crédit Agricole Suisse Open Gstaad CL 31 Aug 3 Washington D.C. -

Florida Women's Tennis
2013-14 Gators (back row, left-to-right): Head Coach Roland Thornqvist, Brianna Morgan, Kourtney Keegan, Stefani Stojic, Belinda Woolcock and Associate Head Coach Dave Balogh; (front row) Program Coordinator Kate Harte, Olivia Janowicz, Sofie Oyen, Alexandra Cercone and Graduate Assistant Athletic Trainer Kelly Needs FLORIDA WOMEN’S TENNIS 2013-14 MEDIA SUPPLEMENT FLORIDA WOMEN’S TENNIS 2013-14 MEDIA SUPPLEMENT CONTENTS / QUICK FACTS 2013-14 SEASON PREVIEW 2013-14 Gator Roster ......................................................3 FLORIDA TENNIS QUICK FACTS (as of Jan. 1, 2014) 2013-14 Gator Schedule ..................................................2 Perry Indoor Facility ........................................................93 G eneral Information SEC Academic Honor Roll (5): .... Alexandra Cercone, Lauren Embree, Caroline Hitimana, Olivia Janowicz, Sofie Oyen Ring Tennis Complex ......................................................91 Location: ......................... Gainesville, Florida UF Quick Facts ................................................................1 SEC Freshman Academic Honor Roll (1): .....Brianna Morgan Est. Population: .............................124,491 ITA Scholar-Athlete (min. 3.5 GPA): ...... Alexandra Cercone MEDIA INFORMATION Founded: ....................................1853 ITA All-Academic Team (minimum 3.2 team GPA): .......yes! Communications Directory, UF ..........................................4 Enrollment: ................................49,785 Directions to Tennis Complex ............................................6 -

ATP World Tour 2019
ATP World Tour 2019 Note: Grand Slams are listed in red and bold text. STARTING DATE TOURNAMENT SURFACE VENUE 31 December Hopman Cup Hard Perth, Australia Qatar Open Hard Doha, Qatar Maharashtra Open Hard Pune, India Brisbane International Hard Brisbane, Australia 7 January Auckland Open Hard Auckland, New Zealand Sydney International Hard Sydney, Australia 14 January Australian Open Hard Melbourne, Australia 28 January Davis Cup First Round Hard - 4 February Open Sud de France Hard Montpellier, France Sofia Open Hard Sofia, Bulgaria Ecuador Open Clay Quito, Ecuador 11 February Rotterdam Open Hard Rotterdam, Netherlands New York Open Hard Uniondale, United States Argentina Open Clay Buenos Aires, Argentina 18 February Rio Open Clay Rio de Janeiro, Brazil Open 13 Hard Marseille, France Delray Beach Open Hard Delray Beach, USA 25 February Dubai Tennis Championships Hard Dubai, UAE Mexican Open Hard Acapulco, Mexico Brasil Open Clay Sao Paulo, Brazil 4 March Indian Wells Masters Hard Indian Wells, United States 18 March Miami Open Hard Miami, USA 1 April Davis Cup Quarterfinals - - 8 April U.S. Men's Clay Court Championships Clay Houston, USA Grand Prix Hassan II Clay Marrakesh, Morocco 15 April Monte-Carlo Masters Clay Monte Carlo, Monaco 22 April Barcelona Open Clay Barcelona, Spain Hungarian Open Clay Budapest, Hungary 29 April Estoril Open Clay Estoril, Portugal Bavarian International Tennis Clay Munich, Germany Championships 6 May Madrid Open Clay Madrid, Spain 13 May Italian Open Clay Rome, Italy 20 May Geneva Open Clay Geneva, Switzerland -

Roland Garros September 26 – October 11, 2020 Women’S Tennis Association Match Notes
ROLAND GARROS SEPTEMBER 26 – OCTOBER 11, 2020 WOMEN’S TENNIS ASSOCIATION MATCH NOTES ROLAND, GARROS, PARIS | SEPTEMBER 27 - OCTOBER 11, 2020 | €38,000,000 GRAND SLAM TOURNAMENT wtatennis.com | facebook.com/WTA | twitter.com/WTA | youtube.com/WTA Tournament Website: www.rolandgarros.com | @rolandgarros | facebook.com/RolandGarros WTA Communications: Adam Lincoln, Estelle LaPorte, Ellie Emerson ROLAND GARROS - ROUND OF 16 (BOTTOM HALF) FIONA FERRO (FRA #49) vs. [4] SOFIA KENIN (USA #6) Kenin leads 1-0 Ferro is in the midst of an 18-match winning streak - 8 at tour level (all on clay)...Kenin is one of two players (also Kvitova) to reach R16 at the three Slams this year [7] PETRA KVITOVA (CZE #11) vs. ZHANG SHUAI (CHN #39) Kvitova leads 3-2 Kvitova is one win away from returning to the Top 10 - she needs to reach QFs which would push her to No.9...A win today would make Zhang just the second Chinese player to post at least three QF runs at majors (also Li Na) [30] ONS JABEUR (TUN #35) vs. DANIELLE COLLINS (USA #57) First meeting With Jabeur’s advancement to the R16, ensures players from five different continents are competing in the fourth round...This is the ninth consecutive year at least one American has reached R16 in Paris LAURA SIEGEMUND (GER #66) vs. PAULA BADOSA (ESP #87) Series tied 1-1 (played in ITFs) Today’s match ensures an unseeded quarterfinalist in Paris for the ninth year in a row...At 32 years old, Siegemund is the fourth oldest player to make her R16 debut in the Open Era THE LAST 16 (BOTTOM HALF) PLAYER RG YTD CAREER -

Match Notes Internationaux De Strasbourg - Strasbourg, France 2021-05-23 - 2021-05-29 | $ 235,238
26/05/2021 SAP Tennis Analytics 1.4.9 MATCH NOTES INTERNATIONAUX DE STRASBOURG - STRASBOURG, FRANCE 2021-05-23 - 2021-05-29 | $ 235,238 1 0 win win 1 matches played 61 Sorana Shuai Cirstea (6) Zhang 45 ROMANIA CHINA 1990-04-07 Date of Birth 1989-01-21 Targoviste, Romania Residence Tianjin, China Right-handed (two-handed backhand) Plays Right-handed (two-handed backhand) 5' 9" (1.76 m) Height 5' 10" (1.77 m) 21 Career-High Ranking 23 $6,064,123 Career Prize Money $6,952,466 $233,024 Season Prize Money $160,240 1 / 2 Singles Titles YTD / Career 0 / 2 47-48 (QF: 2009 Roland Garros) Grand Slam W-L (best) 28-34 (QF: 2019 Wimbledon; 2016 Australian Open) 1-0 / 1-1 (Second round: 2021) YTD / Career STRASBOURG W-L 1-0 / 4-4 (Quarter-Finalist: 2020) (best) 12-6 / 242-252 YTD / Career W-L 1-7 / 178-200 6-1 / 83-77 YTD / Career Clay W-L 1-5 / 31-49 2-1 / 90-75 YTD / Career 3-Set W-L 0-1 / 51-49 3-1 / 56-46 YTD / Career TB W-L 0-1 / 42-45 Champion: Istanbul YTD Best Result Second round: Strasbourg https://dev.saptennis.com/media/mediaportal/#season/2021/events/0406/matches/LS009/apps/post-match-insights/match-notes/snapshots/58b5f… 1/8 26/05/2021 SAP Tennis Analytics 1.4.9 MATCH NOTES INTERNATIONAUX DE STRASBOURG - STRASBOURG, FRANCE 2021-05-23 - 2021-05-29 | $ 235,238 Sorana Shuai Cirstea Zhang Head To Head Record YEAR TOURNAMENT SURFACE ROUND WINNER SCORE/ RESULT TIME 2008 CUNEO CLAY 1r Sorana Cirstea 6-3 4-6 6-3 0m Ranking History TOP RANK YEAR-END YEAR TOP RANK YEAR-END 58 - 2021 35 - 69 86 2020 30 35 72 72 2019 31 46 33 86 2018 27 35 37 37 2017 23 36 81 81 2016 24 24 90 244 2015 61 186 21 93 2014 30 62 21 22 2013 51 51 26 27 2012 120 122 https://dev.saptennis.com/media/mediaportal/#season/2021/events/0406/matches/LS009/apps/post-match-insights/match-notes/snapshots/58b5f… 2/8 26/05/2021 SAP Tennis Analytics 1.4.9 MATCH NOTES INTERNATIONAUX DE STRASBOURG - STRASBOURG, FRANCE 2021-05-23 - 2021-05-29 | $ 235,238 Sorana Shuai Cirstea Zhang Tournament History CURRENT TOURNAMENT CURRENT TOURNAMENT 1r: d. -

Yearbook Yearbook
2010 USTA NORTHERN YEARBOOK Cindy Lim – Girls 12-13 Rapid Rally 4.5 Adult Men’s USTA League Tennis National Champions National Champion Ellie Kantar Brandon Tennis Association Arthur Ashe Essay Contest USTA CTA of the Year National Winner Baseline Tennis Center USTA Organization Member of the Year Elizabeth Walsh www.northern.usta.com Elliott Sprecher Arthur Ashe Essay Contest Nike National 14s Masters Series National Winner Champion 2 2010 USTA Northern Yearbook 2010 YEARBOOK TABLE OF CONTENTS Executive Director Statement/Mission Statement....................................4 President’s Message.................................................................................................5 Councils and Committees........................................................................................5 Board of Directors/Executive Committee....................................................6 USTA Northern Staff.................................................................................................7 USTA Northern Organizational Structure.......................................................8 USTA Northern Diversity Statement.................................................................9 Sponsor Appreciation.............................................................................................11 2009 Organizational Members.......................................................................12 2009 Award Winners............................................................................................14 2009 USTA -

Annual Report 2013 201 3 年
Annual Report 2013 201 3 年 3 月期 アニュアルレポート 2013年 3月期 ソニー株式会社 Annual Report 2013 Business and CSR Review Contents For further information, including video content, please visit Sony’s IR and CSR websites. Letter to Stakeholders: 2 A Message from Kazuo Hirai, President and CEO 16 Special Feature: Sony Mobile 22 Special Feature: CSR at Sony Business Highlights Annual Report 26 http://www.sony.net/SonyInfo/IR/financial/ar/2013/ 28 Sony Products, Services and Content 37 CSR Highlights 55 Financial Section 62 Stock Information CSR/Environment http://www.sony.net/csr/ 63 Investor Information Investor Relations http://www.sony.net/SonyInfo/IR/ Annual Report 2013 on Form 20-F Effective from 2012, Sony has integrated its printed annual http://www.sony.net/SonyInfo/IR/library/sec.html and corporate social responsibility (CSR) reports into Financial Services Business one report that provides essential information on related (Sony Financial Holdings Inc.) developments and initiatives. http://www.sonyfh.co.jp/index_en.html 1 Letter to Stakeholders: A Message from Kazuo Hirai, President and CEO 2 BE MOVED Sony is a company that inspires and fulfills the curiosity of people from around the world, using our unlimited passion for technology, services and content to deliver groundbreaking new excitement and entertainment to move people emotionally, as only Sony can. 3 Fiscal year 2012, ended March 31, 2013, was my first year as President and CEO of Sony. It was a year full of change that enabled us to build positive momentum across the Sony Group. Since becoming President, I visited 45 different Sony Group sites in 16 countries, ranging from electronics sales offices to manufacturing facilities, R&D labs, and entertainment and financial services locations. -

Venus Williams Bio 2016-8-17
Venus Williams On October 31, 1994, a 14-year-old girl, with her hair styled in beads and full of confidence, strode onto the court at Bank of the West Classic in California and transformed tennis. Today, Venus Williams is one of the most accomplished women in the history of the sport. Having been called "the best athlete in the history of women's tennis" by Sports Illustrated, Venus has been ranked number one in the world in singles three times in her career, and has captured seven Grand Slam titles, five Wimbledon championships and five Olympic medals -- and counting. Along the way, Venus has also distinguished herself as a student who has pursued higher education, an entrepreneur who has launched and helms two businesses, a designer who creates fashion and interior designs, an investor whose ventures include becoming with her sister the first African-American women to buy shares of an NFL team, an author who has written a best-selling book, and an advocate for gender and pay equality. The most amazing part is that Venus Williams is just getting started. Venus’ Early Years: Family Values Venus Ebony Starr Williams was born in the Watts area of Los Angeles, California, into a tight-knit family helmed by her parents, Richard Williams and Oracene Price. Born on June 17, 1980, Venus was the fourth of Richard and Oracene’s five daughters. Her birth was followed fifteen months later by the arrival of her youngest sister, Serena. From a young age, Venus’ father, Richard, who himself was self-taught in the sport, began training his daughters on the public tennis courts in Compton, California. -

Veranstaltungskalender 2007 (Änderungen Vorbehalten)
Wettkampf Biel, 5. Dezember 2014 sk Veranstaltungskalender 2015 (Änderungen vorbehalten) Nationale Meisterschaften 06.12. – 07.12.2014 Qualifikationsturniere Junior Champion Trophy Winter 2015 09.01. – 11.01.2015 Junior Champion Trophy (Winter), Kriens (Junioren CH-Hallenmeisterschaften) 05.03. – 08.03.2015 Schroders Senior Champion Trophy (Winter), Birrhard 04.07. – 05.07.2015 Qualifikationsturniere Junior Champion Trophy Sommer 07.07. – 12.07.2015 Junior Champion Trophy (Sommer), Uster (Junioren CH-Meisterschaften) 12.08. – 16.08.2015 Schroders Senior Champion Trophy (Sommer), Scheuren 05.12. – 06.12.2015 Qualifikationsturniere Junior Champion Trophy Winter 2016, Bern 12.12. – 13.12.2015 Qualifikation Swiss Champion Trophy, Biel 17.12. – 20.12.2015 Swiss Champion Trophy, Biel (Schweizer Hallenmeisterschaften der Aktiven) Swiss Tennis-Masters-Turniere 05.09. – 06.09.2015 Nationales Masters Syntax Junior Cup, Biel 07.11. – 08.11.2015 Tour of Champions Schweizer Fleisch Trophy R5-R9 21.11. – 22.11.2015 Tour of Champions Schweizer Fleisch Trophy R4+ 18.12. – 20.12.2015 Nationales Masters Schweizer Fleisch Trophy, Biel Schweizer Fleisch Interclub Finalrunden 15.08. – 16.08.2015 Schweizer Fleisch Interclub Nationalliga A, LTC Winterthur 20.06.2015 Zentraler Finaltag ab 30+, Burgdorf 24.10. – 25.10.2015 Junioren Interclub Finalrunde, Winterthur Tennis Europe und ITF Juniors Turniere in der Schweiz 02.02. – 07.02.2015 Swiss Junior Trophy Winter, Oberentfelden ITF U18 14.02. – 22.02.2015 Stork International TE U14 Trophy, Oetwil am See TE U14 14.02. – 21.02.2015 Scuola Tennis Taverne Junior Cup, Taverne TE U16 13.07. – 19.07.2015 Stork International TE U16 Trophy, Oetwil am See TE U16 20.07. -

Federer, Mike Bryan Seek Milestone Wins on Friday
MERCEDES CUP: DAY 5 MEDIA NOTES Friday, June 10, 2016 TC Weissenhof, Stuttgart, Germany | June 6-12, 2016 Draw: S-28, D-16 | Prize Money: €606,525 | Surface: Grass ATP Info Tournament Info ATP PR & Marketing www.ATPWorldTour.com www.mercedescup.de Martin Dagahs: [email protected] @ATPWorldTour @MercedesCup Press Room: +49 711 32095705 facebook.com/ATPWorldTour facebook.com/MercedesCup FEDERER, MIKE BRYAN SEEK MILESTONE WINS ON FRIDAY QUARTER-FINAL PREVIEW: No. 1 seed Roger Federer could pass Hall-of-Famer Ivan Lendl on Friday and move into second place in the Open Era with 1,072 victories. Federer faces Florian Mayer in the Mercedes Cup quarter-finals, and with a win would trail only Jimmy Connors among the winningest players since the spring of 1968. Federer has a 6-0 FedEx ATP Head 2 Head record against Mayer, including straight-set wins on German grass at the Gerry Weber Open in 2005, 2012 and 2015. Federer is not the only man with a milestone on the line in Stuttgart. Mike Bryan seeks his 1,000th doubles win when he and twin brother Bob face Oliver Marach and Fabrice Martin in a semi-final match on Court 1. Only Federer, Lendl, Connors and Daniel Nestor have earned at least 1,000 victories in singles or doubles. Bob Bryan has 985 doubles wins individually. As a team, the Bryans are 984-300. Also in action are a pair of players who won their first ATP World Tour title in Stuttgart: 2002 champion Mikhail Youzhny and 2008 champion Juan Martin del Potro. -

Spanish Open Dictionary by Jimeno Álvarez VOL12
SPANISH DICTIONARY Jimeno Álvarez Dictionary of meanings generated by www.wordmeaning.org INTRODUCTION www.wordmeaning.org is an open and collaborative dictionary project that, apart from being able to consult meanings of words, also offers its users the possibility of including new words or nuancing the meaning of existing words in it. As is understandable, this project would be impossible to carry out without the esteemed collaboration of the people who follow us around the world. This e-Book, therefore, was born with the intention of paying a small tribute to all our collaborators. Jimeno Álvarez has contributed to the dictionary with 6245 meanings that we have approved and collected in this small book. We hope that the reader is very valuable and if you find it useful or want to be part of the project, do not hesitate to visit our website, we will be delighted to receive you. Working Group www.wordmeaning.org Dictionary of meanings generated by www.wordmeaning.org veña vein in gallegoVenir in Spanish ver alegóricamente see allegorically = Alegoriaalegoria, from the Greek allegorein 'figuratively speaking', is a literary figure or artistic theme that aims to represent an idea by making shapes human, animals or everyday objects.Allegory seeks to give an image that has no image so that it can be better understood by the Government. Draw the abstract, "visible" do what only conceptual, obeys a didactic intention. Thus, a blind woman with a balance, is an allegory of Justice, and a fitted with forgery skeleton is an allegory of death. The creator of allegories usually strive to explain them so that everyone can understand them.