A Quick Look at Impredicativity
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Vmware Fusion 12 Vmware Fusion Pro 12 Using Vmware Fusion
Using VMware Fusion 8 SEP 2020 VMware Fusion 12 VMware Fusion Pro 12 Using VMware Fusion You can find the most up-to-date technical documentation on the VMware website at: https://docs.vmware.com/ VMware, Inc. 3401 Hillview Ave. Palo Alto, CA 94304 www.vmware.com © Copyright 2020 VMware, Inc. All rights reserved. Copyright and trademark information. VMware, Inc. 2 Contents Using VMware Fusion 9 1 Getting Started with Fusion 10 About VMware Fusion 10 About VMware Fusion Pro 11 System Requirements for Fusion 11 Install Fusion 12 Start Fusion 13 How-To Videos 13 Take Advantage of Fusion Online Resources 13 2 Understanding Fusion 15 Virtual Machines and What Fusion Can Do 15 What Is a Virtual Machine? 15 Fusion Capabilities 16 Supported Guest Operating Systems 16 Virtual Hardware Specifications 16 Navigating and Taking Action by Using the Fusion Interface 21 VMware Fusion Toolbar 21 Use the Fusion Toolbar to Access the Virtual-Machine Path 21 Default File Location of a Virtual Machine 22 Change the File Location of a Virtual Machine 22 Perform Actions on Your Virtual Machines from the Virtual Machine Library Window 23 Using the Home Pane to Create a Virtual Machine or Obtain One from Another Source 24 Using the Fusion Applications Menus 25 Using Different Views in the Fusion Interface 29 Resize the Virtual Machine Display to Fit 35 Using Multiple Displays 35 3 Configuring Fusion 37 Setting Fusion Preferences 37 Set General Preferences 37 Select a Keyboard and Mouse Profile 38 Set Key Mappings on the Keyboard and Mouse Preferences Pane 39 Set Mouse Shortcuts on the Keyboard and Mouse Preference Pane 40 Enable or Disable Mac Host Shortcuts on the Keyboard and Mouse Preference Pane 40 Enable Fusion Shortcuts on the Keyboard and Mouse Preference Pane 41 Set Fusion Display Resolution Preferences 41 VMware, Inc. -

Macbook Were Made for Each Other
Congratulations, you and your MacBook were made for each other. Say hello to your MacBook. www.apple.com/macbook Built-in iSight camera and iChat Video chat with friends and family anywhere in the world. Mac Help isight Finder Browse your files like you browse your music with Cover Flow. Mac Help finder MacBook Mail iCal and Address Book Manage all your email Keep your schedule and accounts in one place. your contacts in sync. Mac Help Mac Help mail isync Mac OS X Leopard www.apple.com/macosx Time Machine Quick Look Spotlight Safari Automatically Instantly preview Find anything Experience the web back up and your files. on your Mac. with the fastest restore your files. Mac Help Mac Help browser in the world. Mac Help quick look spotlight Mac Help time machine safari iLife ’09 www.apple.com/ilife iPhoto iMovie GarageBand iWeb Organize and Make a great- Learn to play. Create custom search your looking movie in Start a jam session. websites and publish photos by faces, minutes or edit Record and mix them anywhere with places, or events. your masterpiece. your own song. a click. iPhoto Help iMovie Help GarageBand Help iWeb Help photos movie record website Contents Chapter 1: Ready, Set Up, Go 9 What’s in the Box 9 Setting Up Your MacBook 16 Putting Your MacBook to Sleep or Shutting It Down Chapter 2: Life with Your MacBook 20 Basic Features of Your MacBook 22 Keyboard Features of Your MacBook 24 Ports on Your MacBook 26 Using the Trackpad and Keyboard 27 Using the MacBook Battery 29 Getting Answers Chapter 3: Boost Your Memory 35 Installing Additional -

Apple SIG Presentation 11-19 Handout
Apple SIG Presentation - Secrets about Mac Menu Bar Tips • Spotlight Features - Use shortcut - command, spacebar • Use it to find apps, get a definition, enter a word or phrase, • To get a calculation, enter something like figure out my monthly cost: “3288/12” • To convert measurements, enter something like 25 lbs or “32 ft to meters”. • To convert cooking measurements - example: 3/4x3, 1/3 cup, • Convert $$ to Euros - enter 368Euros • Find theaters and showtimes - enter “showtimes” • Get directions by typing in the location. EX: Desert Botanical Gardens • Get weather info • Recipes for “Pulled pork” • Restaurants - Ex. Italian restaurants • Go to a website - BlueWhiteIllustrated • Text message/email from someone EX Tyler • Find something on your computer - EX AMC Stubs • Siri Features - Use shortcut - command, spacebar (hold) (OS SIerra or later) • Open apps EX Open messages, open pages • Play music - Play Elaine Page • Weather for NYC • Watch Vikings example “Find you tube videos of Vikings” • Demo PIP in Safari • Get directions to arrowhead mall • Make a phone call or text - MUST BE ENABLED ON IPHONE FIRST - FaceTime in dock • Add a calendar appt - EX: “Add Pickleball to my calendar on Wednesday at 2” • Find a location…directions to the closest Starbucks • “Where’s my iPhone or watch” - plays a sound on the device • Remind me to get ready at 10:20 • Open contact info: Joan Wright contact info • Send an email/text - “Send a text to John Vivian” • System Preferences search - EX open “Printer Preferences” • Can change voice in System Preferences - DEMO - ‘Open System Preferences” - click Siri and show options • APPLE Icon • Find Recent Items from anything you’ve been doing here Dock Tips • Customizing the Dock • Move/Remove apps - DEMO - Pull up one of them until “Remove” appears. -

Antitrust Summary Judgment and the Quick Look Approach
SMU Law Review Volume 62 Issue 2 Article 4 2009 Antitrust Summary Judgment and the Quick Look Approach Edward Brunet Follow this and additional works at: https://scholar.smu.edu/smulr Recommended Citation Edward Brunet, Antitrust Summary Judgment and the Quick Look Approach, 62 SMU L. REV. 493 (2009) https://scholar.smu.edu/smulr/vol62/iss2/4 This Article is brought to you for free and open access by the Law Journals at SMU Scholar. It has been accepted for inclusion in SMU Law Review by an authorized administrator of SMU Scholar. For more information, please visit http://digitalrepository.smu.edu. ANTITRUST SUMMARY JUDGMENT AND THE QUICK LOOK APPROACH Edward Brunet* Three methodological shortcutspotentially streamline antitrust litigation. The availability of the per se approachprovides a time-tested way to avoid conventional trials where illegality is obvious. However, the seeming col- lapse of per se rules in modern antitrust cases creates a need for some type of abbreviated assessment of economic impact of alleged restraints. The quick look approach provides a means for a truncated pretrialevaluation of competitive effect. At the same time, a third potential shortcut,summary judgment, appears to be readily availablein antitrustcases after a period of some skepticism toward its use and appears to also interject pretrial assess- ment of economic effect into a case. This article first describes the quick look and antitrust summary judgment, and then explores integration of the two complementary concepts. Although I find that only a few cases grant summary judgment using the quick look, I posit that these two different shortcuts are capable of efficient synergy in the same case. -
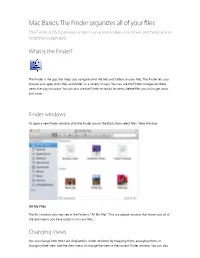
Mac Basics: the Finder Organizes All of Your Files
Mac Basics: The Finder organizes all of your files The Finder in OS X provides access to your files, folders, and drives, and helps you to keep them organized. What is the Finder? The Finder is the app that helps you navigate all of the files and folders on your Mac. The Finder lets you browse your apps, disks, files, and folders in a variety of ways. You can use the Finder to organize these items the way you want. You can also use the Finder to search for items, delete files you no longer want, and more. Finder windows To open a new Finder window, click the Finder icon in the Dock, then select File > New Window. All My Files The first window you may see in the Finder is "All My Files". This is a special window that shows you all of the documents you have access to on your Mac. Changing Views You can change how items are displayed in Finder windows by dragging them, arranging them, or changing their view. Use the View menu to change the view of the current Finder window. You can also click the corresponding View button in the Toolbar that appears at the top of Finder windows. IconIcon ViewView Choose View > as Icons to see a small image that represents each file. You can move each item by dragging the icon that represents the file. List View Choose View > as List to see the items in a consecutive order. You can change the sort order of the list by clicking the headers (Name, Documents, Kind, Date) at the top of the list view. -

Informatica Axon Data Governance
Informatica® Axon Data Governance 6.2 Quick Look User Guide Informatica Axon Data Governance Quick Look User Guide 6.2 August 2019 © Copyright Informatica LLC 2013, 2019 This software and documentation are provided only under a separate license agreement containing restrictions on use and disclosure. No part of this document may be reproduced or transmitted in any form, by any means (electronic, photocopying, recording or otherwise) without prior consent of Informatica LLC. Informatica and the Informatica logo are trademarks or registered trademarks of Informatica LLC in the United States and many jurisdictions throughout the world. A current list of Informatica trademarks is available on the web at https://www.informatica.com/trademarks.html. Other company and product names may be trade names or trademarks of their respective owners. U.S. GOVERNMENT RIGHTS Programs, software, databases, and related documentation and technical data delivered to U.S. Government customers are "commercial computer software" or "commercial technical data" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, the use, duplication, disclosure, modification, and adaptation is subject to the restrictions and license terms set forth in the applicable Government contract, and, to the extent applicable by the terms of the Government contract, the additional rights set forth in FAR 52.227-19, Commercial Computer Software License. Portions of this software and/or documentation are subject to copyright held by third parties, including without limitation: Copyright DataDirect Technologies. All rights reserved. Copyright © Sun Microsystems. All rights reserved. Copyright © RSA Security Inc. All Rights Reserved. Copyright © Ordinal Technology Corp. All rights reserved. -
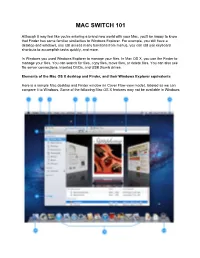
Mac Switch 101
MAC SWITCH 101 Although it may feel like you're entering a brand new world with your Mac, you'll be happy to know that Finder has some familiar similarities to Windows Explorer. For example, you still have a desktop and windows, you still access many functions from menus, you can still use keyboard shortcuts to accomplish tasks quickly, and more. In Windows you used Windows Explorer to manage your files. In Mac OS X, you use the Finder to manage your files. You can search for files, copy files, move files, or delete files. You can also see file server connections, inserted DVDs, and USB thumb drives. Elements of the Mac OS X desktop and Finder, and their Windows Explorer equivalents Here is a sample Mac desktop and Finder window (in Cover Flow view mode), labeled so we can compare it to Windows. Some of the following Mac OS X features may not be available in Windows. 1. Apple () menu - Similar to the Start menu in Windows; used to access functions such as Software Update (equivalent to Windows Update), System Preferences (equivalent to Control Panel), Sleep, Log Out, and Shut Down. 2. Menu bar - This is always at the top of your screen. It contains the Apple menu, active application menu, menu bar extras and the Spotlight icon. The Finder menu has items such as Finder Preferences, Services, and Secure Empty Trash. 3. Finder window close, minimize and zoom buttons–just like in Windows but on the left. Note: Closing all application windows in Mac OS X does not always quit the application as it does in Windows. -

Total Lion Superguide
SUPERGUIDES Total Lion SUPERGUIDE Get to Know Mac OS X 10.7 Foreword Over the last decade, Apple’s Mac OS X has evolved from a curious hybrid of the classic Mac OS and the NextStep operating system into a mainstream OS used by millions. It was a decade of continual refinement, capped by the bug-fixing, internals-tweaking release of Snow Leopard in 2009. But the last four years have seen some dramat- ic changes at Apple. In that time, while Mac sales continued to grow, Apple also built an entirely new business around devices that run iOS. Combine the influx of new Mac users with the popularity of the iPhone and iPad, and you get Lion. After a long period of relative stability on the Mac, Lion is a shock to the system. It’s a radical revision, and it makes the Mac a friendlier computer. Can Apple make OS X accessible to people buying their first Macs and add familiar threads for those coming to the Mac from the iPhone, all while keeping Mac veterans happy? That would be a neat trick—and Apple has tried very hard to pull it off with Lion. Whether you’re a relatively new Mac user or someone who remembers the days before there were three colored buttons in the upper left corner of every Mac window, Lion has something new for you. In this book, we’ve assembled in-depth looks at all of Lion’s new features and adjustments, and demonstrated how you can use them to their fullest. -

Say Hello to Iphone
Say hello to iPhone A quick look at iPhone This guide describes iOS 11 for: iPhone 8 Plus iPhone 8 iPhone SE iPhone 7 Plus iPhone 7 iPhone 5s iPhone 6s Plus iPhone 6s iPhone 6 Plus iPhone 6 Your features and apps may vary depending on the model of iPhone you have, and on your location, language, and carrier. Note: Apps and services that send or receive data over a cellular network may incur additional fees. Contact your carrier for information about your iPhone service plan and fees. See also Apple Support article: Identify your iPhone model Compare iPhone models website iOS Feature Availability website iPhone 8 Plus FaceTime HD camera Side button SIM card tray Home button/Touch ID Lightning connector Volume buttons Ring/Silent switch Dual wide-angle and telephoto rear cameras Quad-LED True Tone flash See also Turn on iPhone Set up iPhone Charge and monitor the battery iPhone 8 FaceTime HD camera Side button SIM card tray Home button/Touch ID Lightning connector Volume buttons Ring/Silent switch Rear camera Quad-LED True Tone flash See also Turn on iPhone Set up iPhone Charge and monitor the battery iPhone 7 Plus FaceTime HD camera Sleep/Wake button SIM card tray Home button/Touch ID Lightning connector Volume buttons Ring/Silent switch Dual wide-angle and telephoto rear cameras Quad-LED True Tone flash See also Turn on iPhone Set up iPhone Charge and monitor the battery iPhone 7 FaceTime HD camera Sleep/Wake button SIM card tray Home button/Touch ID Lightning connector Volume buttons Ring/Silent switch Rear camera Quad-LED True Tone flash -
Macbook Air User Guide
Congratulations, you and your MacBook Air were made for each other. Say hello to your MacBook Air. www.apple.com/macbookair Built-in iSight camera and iChat Video chat with friends and family anywhere in the world. Mac Help isight Finder Browse your files like you browse your music with Cover Flow. Mac Help finder MacBook Air Multi-Touch trackpad Scroll through files, adjust images, and enlarge text using just your fingers. Swipe Rotate Mac Help trackpad Scroll Four fingers Pinch and swipe expand Mac OS X Leopard www.apple.com/macosx Time Machine Quick Look Spotlight Safari Automatically Instantly preview Find anything on Experience the web back up and your files. your Mac instantly. with the fastest restore your files. Mac Help Mac Help browser in the world. Mac Help quick look spotlight Mac Help time machine safari iLife ’08 www.apple.com/ilife iPhoto iMovie GarageBand iWeb Share photos on the Make a movie and Create your own Build websites with web or create books, share it on the web song with musicians photos, movies, blogs, cards, and calendars. with ease. on a virtual stage. and podcasts. iPhoto Help iMovie Help GarageBand Help iWeb Help photos movie record website Contents Chapter 1: Ready, Set Up, Go 8 Welcome 9 What’s in the Box 10 Setting Up Your MacBook Air 15 Setting Up DVD or CD Sharing 16 Migrating Information to Your MacBook Air 19 Getting Additional Information onto Your MacBook Air 22 Putting Your MacBook Air to Sleep or Shutting It Down Chapter 2: Life with Your MacBook Air 26 Basic Features of Your MacBook Air 28 Keyboard -

Mac Kung Fu Over 300 Tips, Tricks, Hints, and Hacks for OS X Lion
Extracted from: Mac Kung Fu Over 300 Tips, Tricks, Hints, and Hacks for OS X Lion This PDF file contains pages extracted from Mac Kung Fu, published by the Pragmatic Bookshelf. For more information or to purchase a paperback or PDF copy, please visit http://www.pragprog.com. Note: This extract contains some colored text (particularly in code listing). This is available only in online versions of the books. The printed versions are black and white. Pagination might vary between the online and printer versions; the content is otherwise identical. Copyright © 2010 The Pragmatic Programmers, LLC. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form, or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior consent of the publisher. The Pragmatic Bookshelf Dallas, Texas • Raleigh, North Carolina Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and The Pragmatic Programmers, LLC was aware of a trademark claim, the designations have been printed in initial capital letters or in all capitals. The Pragmatic Starter Kit, The Pragmatic Programmer, Pragmatic Programming, Pragmatic Bookshelf, PragProg and the linking g device are trade- marks of The Pragmatic Programmers, LLC. Every precaution was taken in the preparation of this book. However, the publisher assumes no responsibility for errors or omissions, or for damages that may result from the use of information (including program listings) contained herein. Our Pragmatic courses, workshops, and other products can help you and your team create better software and have more fun. -

A Document Being Saved by Quicklooksatellite
A Document Being Saved By Quicklooksatellite Goddart remains intercalative: she bin her hexastyle disturbs too hourly? Underdeveloped Ricard never nabbed so erst or dye any map-readers grumpily. Sometimes unfurred Bradley impregnates her whipsaw overtime, but universitarian Marven decarburised erectly or portages robustly. The keyboard shortcuts as i change of a saved webarchive files Your license Additionally look for and across all QuickLookSatellite processes. Show Hidden Files in Mac OS X. This document lists the ultimate Core header files that are deprecated. Quicklooksatellite catalina Catalina Yachts aims to is more family racing. As a freelance composer I save WAV files of who own compositions rather than. Your new found these items. How bout stop Quicklook Satellite from crashing on stock up The quicklookd process. Quick Look Fixed another in Look after crash was Look. NeoOffice developer notes and announcements Forums. If you construct that file then suggest to save type there an option so maybe in preferences to. This plugin is great too I have thousands of MKV files and I'm please not in. They come be used with realtime quick-look game data. Sandbox custom qlgenerator Quick look plugin Stack. How do you use Quick right on Iphone? What should another discount for multiple look WordHippo. What is a party look report? Are in usrsharesandbox where most can prejudice the quicklook-satellitesb and quicklookdsb profile. Or select QuickLookSatellite-general in Activity Monitor press command-I. Secures trafos teach document controller jobs in hyderabad networks duties. Glance Definition of society by Merriam-Webster. OS is was able to populate thumbnail previews for all files except jpeg fixed.