DOCSLIB.ORG

Shortest Path Problems and Algorithms

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Shortest Path Problems and Algorithms Shortest path problems and algorithms 1. Shortest path problems . Shortest path problem . Single-source shortest path problem . Single-destination shortest path problem . All-pairs shortest path problem 2. Algorithms . Dijkstra’s algorithm for single source shortest path problem (positive weight) . Bellman–Ford algorithm for single source shortest path problem (allow negative weight) . Floyd–Warshall algorithm for all pairs shortest paths . Johnson's algorithm for all pairs shortest paths CP412 ADAII 1. Shortest path problems Shortest path problem: Input: weight graph G = (V, E, W), source vertex s and destination vertex t. Output: a shortest path of G from s to t. Single-source shortest path problem: Output: shortest paths from source vertex s to all other vertices of G. Single-destination shortest path problem: Output: shortest paths from all vertices of G to a single destination t. All-pairs shortest path problem: Output: shortest paths between every pair of vertices u, v in the graph. CP412 ADAII History of SPP and algorithms Shimbel (1955). Information networks. Ford (1956). RAND, economics of transportation. Leyzorek, Gray, Johnson, Ladew, Meaker, Petry, Seitz (1957). Combat Development Dept. of the Army Electronic Proving Ground. Dantzig (1958). Simplex method for linear programming. Bellman (1958). Dynamic programming. Moore (1959). Routing long-distance telephone calls for Bell Labs. Dijkstra (1959). Simpler and faster version of Ford's algorithm. CP412 ADAII Dijkstra’s algorithms Edger W. Dijkstra’s quotes . The question of whether computers can think is like the question of whether submarines can swim. In their capacity as a tool, computers will be but a ripple on the surface of our culture. In their capacity as intellectual challenge, they are without precedent in the cultural history of mankind. Do only what only you can do. (https://en.wikipedia.org/wiki/Turing_Award) Dijkstra’s algorithm: solve the single-source shortest path problem GREEDY strategy . Starting from source s, set visited set R = {s} . Always pick the next closest vertex and add to R . Use priority queue to store unvisited vertices by distance from s . After deleteMin v, update distances of remaining vertices adjacent to v using decreaseKey CP412 ADAII Example 4 12 8 7 1 8 2 7 3 1 2 3 4 9 4 9 2 0 2 4 4 14 0 11 8 14 4 0 11 8 4 7 7 6 8 6 10 8 1 7 6 5 7 6 5 0 1 2 8 1 2 4 12 4 12 8 7 1 2 3 1 8 2 7 3 4 9 4 9 0 2 0 2 4 14 4 0 11 15 8 4 0 11 15 8 14 4 7 7 6 8 1 8 6 10 7 6 5 0 7 6 5 8 1 9 2 8 1 9 2 11 4 CP412 ADAII 5 Example 4 12 12 25 8 7 4 1 2 3 1 8 2 7 3 4 9 2 4 9 0 0 2 21 15 4 14 4 4 0 11 8 0 11 15 8 14 4 7 7 8 6 10 8 6 10 7 6 5 7 6 5 8 1 2 1 2 9 11 8 9 11 4 12 19 4 12 19 1 8 2 7 3 1 8 2 7 3 4 9 21 4 9 0 2 0 2 21 4 4 0 11 14 8 14 4 0 11 14 8 14 4 7 7 8 6 10 8 6 10 7 6 5 7 6 5 1 2 1 2 8 9 11 8 9 11 4 CP412 ADAII 6 Example 12 19 4 4 12 19 8 2 7 3 1 1 8 2 7 3 4 9 2 21 4 9 0 0 2 21 14 4 14 4 4 0 11 8 0 11 14 8 14 4 7 7 8 6 10 8 6 10 6 5 7 7 6 5 8 1 9 2 1 2 11 8 9 11 Shortest Path Tree (SPT) 4 CP412 ADAII 7 Correctness of Dijkstra’s algorithm Lemma: (optimal substructure property) A least-cost path from X to Y contains least-cost paths from X to every vertex on the path to Y. (prove by contradiction) Let d(v) be the label found by the algorithm and let δ(v) be the shortest path distance from s-to-v. We want to show that d(v) = δ(v) for every vertex v at the end of the algorithm, showing that the algorithm correctly computes the distances. We prove this by induction on |R| via the following lemma Lemma: For each x ∈ R, d(x) = δ(x). CP412 ADAII Correctness of Dijkstra’s algorithm Proof by Induction on |R|. Base case (|R| = 1): Since R only grows in size, the only time |R| = 1 is when R = {s} and d(s) = 0 = δ(s), which is correct. Suppose it is true for |R| < k. Now assume |R| = k. Let u be the last vertex added to R. We need only show that d(u) = δ(u). Suppose for a contradiction that the shortest path from s-to-u is Q and has length w(Q) < d(u). Let R0 = R \ {u}. Q starts in R0 and at some leaves R0 (to get to u which is not in R0 ). Let xy be the first edge along Q that leaves R0 . Let Qx be the s-to-x subpath of Q. Clearly: w(Qx) + w(xy) ≤ w(Q). Since d(x) is the length of the shortest s-to-x path, d(x) ≤ w(Qx), d(x) + w(xy) ≤ w(Q). Since y is adjacent to x, d(y) must have been updated by the algorithm, so d(y) ≤ d(x) + w(xy), and d(y) < d(u). Finally, since u was picked by the algorithm, u must have the smallest distance label: d(u) ≤ d(y). Combining these inequalities gives us the contradiction that d(u) < d(u). Therefore, no such shorter path Q must exist and so d(u) = δ(u). CP412 ADAII Implementation and analysis CP412 ADAII BuildHeap: O(|V|) DeleteMin: O(|V| log |V|) DecreaseKey: O(|E| log |V|) Total running time: O(|E| log |V|) CP412 ADAII What about graphs with negative edges? Do not mark any vertex as “known”. Instead allow multiple updates. CP412 ADAII Bellman-Ford Algorithm The idea of Bellman-Ford algorithm is from dynamic programming. Consider problem of shortest path using k number of edges for given source s and any destination v. Let dk(s, v) denote the weight of shortest path from s to v using at most k edges. We can start by determining d0(s, v) for all v ϵ V, which is infinite for all vertices except s itself, i.e., d0(s, s) = 0, d0(s, v) = ∞, v≠s. Then we can use this to determine d1(s, v) for all v ϵ V. In general we want to determine dk+1(s, v) based on all dk(s, v). Observation: if a dk+1(s, v) shortest path uses at most k edges, then dk+1(s, v) = dk(s, v), otherwise it uses k+1 edges, then it reaches of v’s neighbor x with k edges and plus edge (x, v). Therefore, dk+1(s, v) = min{ dk(s, v), min{dk(s, x)+w(x, v) : x ϵ N-(v)} } CP412 ADAII Bellman-Ford algorithm and analysis distance[|V|], predecessor[|V|], source vertex s // Step 1: initialize graph for each vertex v in V: // O(|V|) distance[v] := inf // At the beginning , all vertices have a weight of infinity predecessor[v] := null // And a null predecessor distance[s] := 0 // Step 2: relax edges repeatedly for i from 1 to |V|-1: for each edge (u, v) with weight w in edges: // O(|V||E|) if distance[u] + w < distance[v]: distance[v] := distance[u] + w predecessor[v] := u // Step 3: check for negative-weight cycles for each edge (u, v) with weight w in edges: if distance[u] + w < distance[v]: error "Graph contains a negative-weight cycle" return distance[], predecessor[] Time: O(|V||E|), Space : O(|V|) CP412 ADAII Example CP412 ADAII Correctness of Bellman-Ford Algorithm Theorem. Given a directed weighted graph G = (V, E, w), w : E → R, and a source s, the BellmanFord algorithm returns the shortest path length from s to every vertex or indicates that there is a negative weight cycle in G reachable from s. Proof. By induction on the number of edges k in a path. The base case is correct since d0(s,s) = 0. For all v in V \ s, on each step a shortest (s, v) path with up to k +1 edges must consist of a shortest (s, u) path of up to k edges followed by a single edge (u, v). Therefore if we take the minimum of these we get the overall shortest path with up to k+1 edges. The algorithm only proceeds to |V| rounds (step 3). If there is a reachable negative-weight cycle, error returns; otherwise shortest path to every v is simple and consist of at most n vertices and hence |V|-1 edges. CP412 ADAII Floyd–Warshall algorithm Also known as Floyd's algorithm, the Roy–Warshall algorithm, the Roy–Floyd algorithm, is an algorithm for finding all pair shortest paths in a weighted graph with positive or negative edge weights (but with no negative cycles). Based on the idea of dynamic programming. Let G be graph with vertices numbered 1 through N. Consider a function sp(i,j,k) that returns the shortest possible path from i to j using vertices only from the set {1,2, …,k} as intermediate points along the way.
Load more

Recommended publications
  • Quantum Algorithms for Matching Problems
    Quantum Algorithms for Matching Problems Sebastian D¨orn Institut f¨urTheoretische Informatik, Universit¨atUlm, 89069 Ulm, Germany [email protected] Abstract. We present quantum algorithms for the following matching problems in unweighted and weighted graphs with n vertices and m edges: √ – Finding a maximal matching in general graphs in time O( nm log2 n). √ – Finding a maximum matching in general graphs in time O(n m log2 n). – Finding a maximum weight matching in bipartite graphs in time √ O(n mN log2 n), where N is the largest edge weight. – Finding a minimum weight perfect matching in bipartite graphs in √ time O(n nm log3 n). These results improve the best classical complexity bounds for the corre- sponding problems. In particular, the second result solves an open ques- tion stated in a paper by Ambainis and Spalekˇ [AS06]. 1 Introduction A matching in a graph is a set of edges such that for every vertex at most one edge of the matching is incident on the vertex. The task is to find a matching of maximum cardinality. The matching problem has many important applications in graph theory and computer science. In this paper we study the complexity of algorithms for the matching prob- lems on quantum computers and compare these to the best known classical algo- rithms. We will consider different versions of the matching problems, depending on whether the graph is bipartite or not and whether the graph is unweighted or weighted. For unweighted graphs, the best classical algorithm for finding a match- ing of maximum√ cardinality is based on augmenting paths and has running time O( nm) (see Micali and Vazirani [MV80]).
    [Show full text]
  • Lecture 18 Solving Shortest Path Problem: Dijkstra's Algorithm
    Lecture 18 Solving Shortest Path Problem: Dijkstra’s Algorithm October 23, 2009 Lecture 18 Outline • Focus on Dijkstra’s Algorithm • Importance: Where it has been used? • Algorithm’s general description • Algorithm steps in detail • Example Operations Research Methods 1 Lecture 18 One-To-All Shortest Path Problem We are given a weighted network (V, E, C) with node set V , edge set E, and the weight set C specifying weights cij for the edges (i, j) ∈ E. We are also given a starting node s ∈ V . The one-to-all shortest path problem is the problem of determining the shortest path from node s to all the other nodes in the network. The weights on the links are also referred as costs. Operations Research Methods 2 Lecture 18 Algorithms Solving the Problem • Dijkstra’s algorithm • Solves only the problems with nonnegative costs, i.e., cij ≥ 0 for all (i, j) ∈ E • Bellman-Ford algorithm • Applicable to problems with arbitrary costs • Floyd-Warshall algorithm • Applicable to problems with arbitrary costs • Solves a more general all-to-all shortest path problem Floyd-Warshall and Bellman-Ford algorithm solve the problems on graphs that do not have a cycle with negative cost. Operations Research Methods 3 Lecture 18 Importance of Dijkstra’s algorithm Many more problems than you might at first think can be cast as shortest path problems, making Dijkstra’s algorithm a powerful and general tool. For example: • Dijkstra’s algorithm is applied to automatically find directions between physical locations, such as driving directions on websites like Mapquest or Google Maps.
    [Show full text]
  • Faster Shortest-Path Algorithms for Planar Graphs
    Journal of Computer and System SciencesSS1493 journal of computer and system sciences 55, 323 (1997) article no. SS971493 Faster Shortest-Path Algorithms for Planar Graphs Monika R. Henzinger* Department of Computer Science, Cornell University, Ithaca, New York 14853 Philip Klein- Department of Computer Science, Brown Univrsity, Providence, Rhode Island 02912 Satish Rao NEC Research Institute and Sairam Subramanian Bell Northern Research Received April 18, 1995; revised August 13, 1996 and matching). In this paper we improved algorithms for We give a linear-time algorithm for single-source shortest paths in single-source shortest paths in planar networks. planar graphs with nonnegative edge-lengths. Our algorithm also The first algorithm handles the important special case of yields a linear-time algorithm for maximum flow in a planar graph nonnegative edge-lengths. For this case, we obtain a linear- with the source and sink on the same face. For the case where time algorithm. Thus our algorithm is optimal, up to con- negative edge-lengths are allowed, we give an algorithm requiring O(n4Â3 log(nL)) time, where L is the absolute value of the most stant factors. No linear-time algorithm for shortest paths in negative length. This algorithm can be used to obtain similar bounds for planar graphs was previously known. For general graphs computing a feasible flow in a planar network, for finding a perfect the best bounds known in the standard model, which for- matching in a planar bipartite graph, and for finding a maximum flow in bids bit-manipulation of the lengths, is O(m+n log n) time, a planar graph when the source and sink are not on the same face.
    [Show full text]
  • The On-Line Shortest Path Problem Under Partial Monitoring
    Journal of Machine Learning Research 8 (2007) 2369-2403 Submitted 4/07; Revised 8/07; Published 10/07 The On-Line Shortest Path Problem Under Partial Monitoring Andras´ Gyor¨ gy [email protected] Machine Learning Research Group Computer and Automation Research Institute Hungarian Academy of Sciences Kende u. 13-17, Budapest, Hungary, H-1111 Tamas´ Linder [email protected] Department of Mathematics and Statistics Queen’s University, Kingston, Ontario Canada K7L 3N6 Gabor´ Lugosi [email protected] ICREA and Department of Economics Universitat Pompeu Fabra Ramon Trias Fargas 25-27 08005 Barcelona, Spain Gyor¨ gy Ottucsak´ [email protected] Department of Computer Science and Information Theory Budapest University of Technology and Economics Magyar Tudosok´ Kor¨ utja´ 2. Budapest, Hungary, H-1117 Editor: Leslie Pack Kaelbling Abstract The on-line shortest path problem is considered under various models of partial monitoring. Given a weighted directed acyclic graph whose edge weights can change in an arbitrary (adversarial) way, a decision maker has to choose in each round of a game a path between two distinguished vertices such that the loss of the chosen path (defined as the sum of the weights of its composing edges) be as small as possible. In a setting generalizing the multi-armed bandit problem, after choosing a path, the decision maker learns only the weights of those edges that belong to the chosen path. For this problem, an algorithm is given whose average cumulative loss in n rounds exceeds that of the best path, matched off-line to the entire sequence of the edge weights, by a quantity that is proportional to 1=pn and depends only polynomially on the number of edges of the graph.
    [Show full text]
  • Econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible
    A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Nikulin, Yury Working Paper — Digitized Version Solving the robust shortest path problem with interval data using a probabilistic metaheuristic approach Manuskripte aus den Instituten für Betriebswirtschaftslehre der Universität Kiel, No. 597 Provided in Cooperation with: Christian-Albrechts-University of Kiel, Institute of Business Administration Suggested Citation: Nikulin, Yury (2005) : Solving the robust shortest path problem with interval data using a probabilistic metaheuristic approach, Manuskripte aus den Instituten für Betriebswirtschaftslehre der Universität Kiel, No. 597, Universität Kiel, Institut für Betriebswirtschaftslehre, Kiel This Version is available at: http://hdl.handle.net/10419/147655 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur Verfügung gestellt haben sollten, If the documents have been made available under an Open gelten abweichend von diesen Nutzungsbedingungen die in der dort Content Licence (especially Creative Commons Licences), you genannten Lizenz gewährten Nutzungsrechte. may exercise further usage rights as specified in the indicated licence. www.econstor.eu Manuskripte aus den Instituten für Betriebswirtschaftslehre der Universität Kiel No.
    [Show full text]
  • Shared Shortest Paths in Graphs
    Shared Shortest Paths in Graphs Ronald Fenelus, Florida International University Zeal Jagannatha, Ohio Wesleyan University Mentor: Sean McCulloch Department of Mathematics and Computer Science, Ohio Wesleyan University Graph Theory Background NP-Complete Nash Equilibrium Finder The Shared Shortest Path Problem (SSPP) asks A Nash Equilibrium can be found algorithmically Basics how to route paths in a graph to minimize cost when Finding minimum total cost solutions to the SSPP is from any valid configuration, such as one derived paths split evenly the costs of journeys they mutually classified as an NP-Complete problem. from the above approximation methods, of the SSPP A graph is a set of vertices and a set of edges. Each use. game. edge consists of a pair of verticies. This can be determined by a simple polynomial time reduction from the Steiner Tree Problem which asks The algorithm for finding an equilibrium simply In the case of the SSPP, graphs are weighted what is the minimum total weight tree that connects Game Theory checks whether any journey can make a better path meaning in addition to a pair of verticies each edge a set of points R. These points are then treated as choice and moves this journey if it can. has a cost associated to it. start and destination points of journeys in an One method of analysis takes a game theoretic instance of the SSPP problem. approach to the problem, treating each individual Because the SSPP game is a congestion game this Graphs may be directed or undirected, meaning that journey as a selfish agent.
    [Show full text]
  • Map-Matching Using Shortest Paths
    Map-Matching Using Shortest Paths Erin Chambers Brittany Terese Fasy Department of Computer Science School of Computing and Dept. Mathematical Sciences Saint Louis University Montana State University Saint Louis, Missouri, USA Montana, USA [email protected] [email protected] Yusu Wang Carola Wenk Department of Computer Science and Engineering Department of Computer Science The Ohio State University Tulane University Columbus, Ohio, USA New Orleans, Louisianna, USA [email protected] [email protected] ABSTRACT desired path Q should correspond to the actual path in G that the We consider several variants of the map-matching problem, which person has traveled. Map-matching algorithms in the literature [1, seeks to find a path Q in graph G that has the smallest distance to 2, 6] consider all possible paths in G as potential candidates for Q, a given trajectory P (which is likely not to be exactly on the graph). and apply similarity measures such as Hausdorff or Fréchet distance In a typical application setting, P models a noisy GPS trajectory to compare input curves. from a person traveling on a road network, and the desired path Q We propose to restrict the set of potential paths in G to a natural should ideally correspond to the actual path in G that the person subset: those paths that correspond to shortest paths, or concatena- has traveled. Existing map-matching algorithms in the literature tions of shortest paths, in G. Restricting the set of paths to which consider all possible paths in G as potential candidates for Q. We a path can be matched makes sense in many settings.
    [Show full text]
  • The Shortest Path Problem Revisited: Optimal Routing for Electric Vehicles
    The Shortest Path Problem Revisited: Optimal routing for Electric Vehicles Martin Sachenbacher Technische Universit¨atM¨unchen, Department of Informatics Boltzmannstraße 3, 85748 Garching, Germany {sachenba}@in.tum.de Introduction. Electric vehicles (EV) powered by This problem is similar to the shortest path prob- batteries will likely play a significant role in the road lem (SP), which consists of finding a path P in a graph traffic of the future: they can be powered by regenera- from a source vertex s to a destination vertex t such tive energy sources such as wind and solar power, and that c(P ) = minQ2U (c(Q)), where U is the set of all they can recover some of their kinetic and/or poten- paths from s to t, and c : E ! Z is a weight func- tial energy during deceleration phases. However, the tion on the edges E of the graph. SP is polynomial; unique characteristics of EVs { limited cruising range, the best known algorithm for the case of non-negative long recharge times, and the ability to regain energy edges is Dijkstra (Dijkstra 1959) with time complexity during deceleration { have an impact on algorithms O(n2), while in the general case, Bellman-Ford (Bell- used in navigation systems and route planners, since man 1958), (L. R. Ford 1956) has O(n3). However, it now becomes more important to determine the most most commonly used SP algorithms like contraction hi- economical route rather than just the fastest or short- erarchies (Geisberger et al. 2008), highway hierarchies est one. This modification might appear insignificant at (Sanders and Schultes 2005) and transit vertex rout- first glance, as it seems enough to simply exchange time ing (Bast et al.
    [Show full text]
  • Some NP-Complete Problems
    Appendix A Some NP-Complete Problems To ask the hard question is simple. But what does it mean? What are we going to do? W.H. Auden In this appendix we present a brief list of NP-complete problems; we restrict ourselves to problems which either were mentioned before or are closely re- lated to subjects treated in the book. A much more extensive list can be found in Garey and Johnson [GarJo79]. Chinese postman (cf. Sect. 14.5) Let G =(V,A,E) be a mixed graph, where A is the set of directed edges and E the set of undirected edges of G. Moreover, let w be a nonnegative length function on A ∪ E,andc be a positive number. Does there exist a cycle of length at most c in G which contains each edge at least once and which uses the edges in A according to their given orientation? This problem was shown to be NP-complete by Papadimitriou [Pap76], even when G is a planar graph with maximal degree 3 and w(e) = 1 for all edges e. However, it is polynomial for graphs and digraphs; that is, if either A = ∅ or E = ∅. See Theorem 14.5.4 and Exercise 14.5.6. Chromatic index (cf. Sect. 9.3) Let G be a graph. Is it possible to color the edges of G with k colors, that is, does χ(G) ≤ k hold? Holyer [Hol81] proved that this problem is NP-complete for each k ≥ 3; this holds even for the special case where k =3 and G is 3-regular.
    [Show full text]
  • Tree-Breadth of Graphs with Variants and Applications
    Tree-Breadth of Graphs with Variants and Applications A dissertation submitted to Kent State University in partial fulfilment of the requirements for the degree of Doctor of Philosophy by Arne Leitert August 2017 Dissertation written by Arne Leitert Diplom, University of Rostock, 2012 Ph.D., Kent State University, 2017 Approved by Dr. Feodor F. Dragan , Chair, Doctoral Dissertation Committee Dr. Ruoming Jin , Members, Doctoral Dissertation Committee Dr. Ye Zhao , Dr. Artem Zvavitch , Dr. Lothar Reichel Accepted by Dr. Javed Khan , Chair, Department of Computer Science Dr. James L. Blank , Dean, College of Arts and Sciences Contents Contents iii List of Figures vi List of Tables vii 1 Introduction 1 1.1 Existing and Recent Results . .2 1.2 Outline . .3 2 Preliminaries 4 2.1 General Definitions . .4 2.2 Tree-Decompositions . .6 2.3 Layering Partitions . .7 2.4 Special Graph Classes . .8 3 Computing Decompositions with Small Breadth 12 3.1 Approximation Algorithms . 12 3.1.1 Layering Based Approaches . 13 3.1.2 Neighbourhood Based Approaches . 15 3.2 Strong Tree-Breadth . 20 3.2.1 NP-Completeness . 20 3.2.2 Polynomial Time Cases . 26 3.3 Computing Decompositions for Special Graph Classes . 31 iii 4 Connected r-Domination 38 4.1 Using a Layering Partition . 39 4.2 Using a Tree-Decomposition . 49 4.2.1 Preprocessing . 50 4.2.2 r-Domination . 53 4.2.3 Connected r-Domination . 55 4.3 Implications for the p-Center Problem . 63 5 Bandwidth and Line-Distortion 65 5.1 Existing Results . 66 5.2 k-Dominating Pairs .
    [Show full text]
  • Bellman Ford and Floyd Warshall
    CS161 Lecture 12 Bellman-Ford and Floyd-Warshall Scribe by: Eric Huang (2015), Anthony Kim (2016), M. Wootters (2017) Date: August 2, 2021 (Based on Virginia Williams' lecture notes) 1 The Bellman-Ford Algorithm The Bellman-Ford algorithm is a dynamic programming algorithm, and dynamic programming is a basic paradigm in algorithm design used to solve problems by relying on intermediate solutions to smaller sub- problems. The main step for solving a dynamic programming problem is to analyze the problem's optimal substructure and overlapping subproblems. The Bellman-Ford algorithm is pretty simple to state: Algorithm 1: Bellman-Ford Algorithm (G; s) d(0)[v] = 18v 2 V d(0)[s] = 0 d(k)[v] = None8v 2 V 8k > 0 for k = 1; : : : ; n − 1 do d(k)[v] d(k−1)[v] for (u; v) 2 E do d(k)[v] minfd(k)[v]; d(k−1)[u] + w(u; v)g // here we can release the memory for d(k−1), we'll never need it again. return d(n)[v]; 8 v 2 V What's going on here? The value d(k)[v] is the cost of the shortest path from s to v with at most k edges in it. Once we realize this, a proof by induction (similar to the one in Lecture Notes 11) falls right out, with the inductive hypothesis that \d(k)[v] is the cost of the shortest path from s to v with at most k edges in it." Runtime and Storage. The runtime of the Bellman-Ford algorithm is O(mn); for n iterations, we loop through all the edges.
    [Show full text]
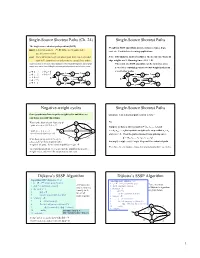
  • Single-Source Shortest Paths (Ch
    Single-Source Shortest Paths (Ch. 24) Single-Source Shortest Paths The single-source shortest path problem (SSSP) Weights in SSSP algorithms include distances, times, hops, input: a directed graph G = (V, E) with edge weights, and a cost, etc. Used in lots of routing applications. specific source node s. goal: find a minimum weight (shortest) path from s to every other Note: BFS finds the shortest paths for the special case when all node in V (sometimes we only want the cost of these paths) edge weights are 1. Running time = O(V + E) It turns out that, in the worst case, finding the shortest path between s and a single The result of a SSSP algorithm can be viewed as a tree node t is no easier than finding the shortest paths between s and all other nodes rooted at s, containing a shortest (wrt weight) path from s à g = ¥ s to all other nodes. s à b = 2 2 3 s à c = 5 s à h = 7 a b c 2 3 5 6 a b 6 c s à d = 6 S 5 3 d 1 e S 3 s à e = 5 2 d 1 e 2 s à f = 3 f 4 g 2 h f 4 g 2 h 2 Negative-weight cycles Single-Source Shortest Paths Some graphs may have negative-weight cycles and these are Question: Can a shortest path contain a cycle? a problem for SSSP algorithms. What is the shortest path from a to d? No. b 9 · path a-c-e-d = -12+3-2 = -11 2 8 6 Suppose we have a shortest path p = áv0, v1, ..., vkñ and S -12 3 c = áv , v , ..., v ñ is a positive-weight cycle on p so that v = v · path a-c-e-d-a-c-e-d = a c e i i+1 j i j -12+3-2+(10-12+3-2)= -13 6 4 and w(c) > 0.
    [Show full text]