DOCSLIB.ORG

Object-Oriented Programming in Smalltalk

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Object-Oriented Programming in Smalltalk Object-Oriented Programming in Smalltalk COMP 105 Assignment Due Tuesday, April 30, 2019 at 11:59PM Contents Overview 2 Setup 2 Getting to know 휇Smalltalk interactively ........................... 2 Analyzing your code for potential faults ............................ 3 Assembling documentation for the assignment ........................ 5 Reading comprehension (10 percent) 5 Individual Problem 9 Pair Problems: Bignum arithmetic 10 Big picture of the solution ................................... 10 How to prepare your code for our testing ........................... 10 Unit testing bignums in Smalltalk ............................... 10 Using check-expect .................................. 11 Using check-print ................................... 11 Our unit tests ....................................... 11 Details of all the problems ................................... 12 Two simple sanity checks for multiplication .......................... 17 More advice about testing natural numbers .......................... 19 Hints and guidelines from past students ............................ 20 Other hints and guidelines ................................... 21 The whole story about division ................................ 21 Avoid common mistakes .................................... 22 Extra credit 23 What and how to submit: Individual problem 24 What and how to submit: Pair problems 24 How your work will be evaluated 25 1 Overview Object-oriented programming has been popular since the 1990s, and like lambdas, object-oriented fea- tures are found everywhere. But these features are not always easy to tease out: many object-oriented languages, such as Java and C++, are hybrids, which mix objects with abstract data types or other no- tions of encapsulation and modularity. When you don’t already know how to program with objects, hybrid designs are more confusing than helpful. For that reason, we study pure objects, as popularized by Smalltalk: even simple algorithms send lots of messages back and forth among a cluster of cooper- ating, communicating objects. Popular languages that use similar models include Ruby, JavaScript, and Objective C. The assignment is divided into three parts. • You begin with reading comprehension. • You do a small warmup problem, which acquaints you with pure object-oriented style and with 휇Smalltalk’s large initial basis. • You implement bignums in 휇Smalltalk. As in the SML assignment, you will implement both natural numbers and signed integers. You will also use object-oriented dispatch to implement “mixed arithmetic” of large and small integers—a useful abstraction that demonstrates the “open” nature of true object-oriented systems. This assignment is time-consuming. Many students have experience in languages called “object- oriented,” but few students have experience with the extensive inheritance and pervasive dynamic dispatch that characterize idiomatic Smalltalk programs. Setup The 휇Smalltalk interpreter is in /comp/105/bin/usmalltalk. Many useful 휇Smalltalk sources are in- cluded the book’s git repository, which you can clone by git clone homework.cs.tufts.edu:/comp/105/build-prove-compare Sources that can be found in the examples directory includes copies of predefined classes, collection classes, shape classes, and other examples from the textbook. Getting to know 휇Smalltalk interactively Smalltalk is a little language with a big initial basis; there are lots of predefined classes and methods. To help you work with the big basis, as well as to debug your own code, we recommend two tools: • Every class understands the messages protocol and localProtocol. These methods are shown in Figure 10.8 on page 826. They provide a quick way to remind yourself what messages an object understands and how the message names are spelled. To learn a protocol the lazy person’s way, send an object every message in its protocol, just to see what happens. You might get a stack trace, but that will help you learn. • The interpreter can help you debug by emitting a call trace of up to n message sends and answers. Just enter the definition (val &trace n) 2 at the read-eval-print loop. To turn tracing off, (set &trace 0). Here is an (abbreviated) example trace of message new sent to class List, which is the subject of one of the reading-comprehension questions: -> (new List) standard input, line 3: Sending message (new) to class List predefined, line 478: Sending message (new) to class SequenceableCollection predefined, line 478: (new <class List>) = <List> predefined, line 478: Sending message (new) to class ListSentinel predefined, line 469: Sending message (new) to class Cons predefined, line 469: (new <class ListSentinel>) = <ListSentinel> predefined, line 470: Sending message (pred: <ListSentinel>) to an object of class ListSentinel predefined, line 470: (pred: <ListSentinel> <ListSentinel>) = <ListSentinel> predefined, line 471: Sending message (cdr: <ListSentinel>) to an object of class ListSentinel predefined, line 471: (cdr: <ListSentinel> <ListSentinel>) = <ListSentinel> predefined, line 478: (new <class ListSentinel>) = <ListSentinel> predefined, line 478: Sending message (sentinel: <ListSentinel>) to an object of class List predefined, line 478: (sentinel: <List> <ListSentinel>) = <List> standard input, line 3: (new <class List>) = <List> <trace ends> List( ) One warning: as usual, the interpreter responds to an expression evaluation by printing the re- sult. But in Smalltalk, printing is achieved by sending the println message to the result object. This interaction is also traced, and the results can be startling. Here, for example, is the result of evaluating the literal integer 3: -> 3 internally generated SEND node, line 1: Sending message (println) to object of class SmallInteger internal expression ”(begin (print self) (print newline) self)”, line 1: Sending message (print) to object of class SmallInteger 3 internal expression ”(begin (print self) (print newline) self)”, line 1: (print 3<SmallInteger>) = 3<SmallInteger> internal expression ”(begin (print self) (print newline) self)”, line 1: Sending message (print) to object of class Char predefined classes, line 229: Sending message (printu) to object of class SmallInteger predefined classes, line 229: (printu 10<SmallInteger>) = 10<SmallInteger> internal expression ”(begin (print self) (print newline) self)”, line 1: (print <Char>) = 10<SmallInteger> internally generated SEND node, line 1: (println 3<SmallInteger>) = 3<SmallInteger> As you see, even a simple operation like printing a number involves four message sends. Don’t let them confuse you. Analyzing your code for potential faults Smalltalk has no type system. But you can still check some properties of your code. • A “wrong number of arguments” check is built into the language. A symbolic message like + or != expects exactly one argument, plus the receiver. An alphanumeric message like println or ifTrue:ifFalse: expects a number of arguments equal to the number of colons in the message’s name—plus the receiver. If these expectations aren’t met, the offending code is flagged with a syntax error. 3 • We provide a simple static-analysis tool called lint-usmalltalk. It checks each message send to be sure a method with that name is defined somewhere. If no such method is defined, the message name is misspelled. Normally, lint-usmalltalk also checks for unused methods. An unused method might be mis- spelled, or it might just be one that isn’t used in any code or test. Here’s an example run: % lint-usmalltalk bignum.smt instance method compare: of class Natural is never used anywhere instance method smod: of class Natural is never used anywhere • There is a static analysis you can do yourself called call-graph analysis. It can help you understand how classes work together, and it’s the best tool for diagnosing problems with infinite loops and recursions. Call-graph analysis works by identifying what methods transfer control to what other methods. Every node in the call graph is a combination of class name and message name. For example, Boolean/ifTrue: or List/select:. Each node has outgoing edges that illustrate what happens if the node’s message is sent to an instance of the node’s class:1 1. If the message is implemented by a primitive method, like + on SmallInteger, it has no outgoing edges. 2. If the method is inherited from the superclass, the node has a dotted edge to the same message on the superclass. For example, node True/ifTrue: has a dotted edge to Boolean/ifTrue:. 3. If the method is a subclass responsibility, the node has a dotted edge to each subclass. 4. If the method is defined on the class, the node has a solid outgoing edge for each message that could be sent during the method’s execution. You have to look at each message send and figure out what class of object it might be sent to. This part can’t easily be determined by looking at the code; you have to know the protocol. For example, if message & is sent to a Boolean, we know the argument is also a Boolean. As another example, if message + is sent to a natural number, the protocol says the argument obeys the Natural protocol. Usually all the possibilities are covered by a superclass. For example, even though message size could be sent to a List or an Array, you can just draw a single edge to node Col- lection/size. Sometimes you might have more then one outgoing edge per message—for example, if a message could be sent to an Integer or a Fraction, but not to any Number. 5. If the method is not defined and not inherited from a superclass, the message is not under- stood, and your program is broken. Here are some tips about call graphs: – If you have a cycle in the graph, it represents a potential recursion. Be sure that on every trip through the cycle, some argument or some receiver is getting smaller, or that the algo- rithm is making progress in some other way. For example, my code for * on class Natural can sometimes send the * message to a natural number, but on every trip through this cycle, the receiver of * gets smaller (by a factor of 푏). 1If you encounter a class method, just call the message something like “class method new,” and proceed as you would otherwise. 4 – Have a goal in mind, and ignore messages that are unrelated to the goal.
Load more

Recommended publications
  • Understanding Integer Overflow in C/C++
    Appeared in Proceedings of the 34th International Conference on Software Engineering (ICSE), Zurich, Switzerland, June 2012. Understanding Integer Overflow in C/C++ Will Dietz,∗ Peng Li,y John Regehr,y and Vikram Adve∗ ∗Department of Computer Science University of Illinois at Urbana-Champaign fwdietz2,[email protected] ySchool of Computing University of Utah fpeterlee,[email protected] Abstract—Integer overflow bugs in C and C++ programs Detecting integer overflows is relatively straightforward are difficult to track down and may lead to fatal errors or by using a modified compiler to insert runtime checks. exploitable vulnerabilities. Although a number of tools for However, reliable detection of overflow errors is surprisingly finding these bugs exist, the situation is complicated because not all overflows are bugs. Better tools need to be constructed— difficult because overflow behaviors are not always bugs. but a thorough understanding of the issues behind these errors The low-level nature of C and C++ means that bit- and does not yet exist. We developed IOC, a dynamic checking tool byte-level manipulation of objects is commonplace; the line for integer overflows, and used it to conduct the first detailed between mathematical and bit-level operations can often be empirical study of the prevalence and patterns of occurrence quite blurry. Wraparound behavior using unsigned integers of integer overflows in C and C++ code. Our results show that intentional uses of wraparound behaviors are more common is legal and well-defined, and there are code idioms that than is widely believed; for example, there are over 200 deliberately use it.
    [Show full text]
  • Collecting Vulnerable Source Code from Open-Source Repositories for Dataset Generation
    applied sciences Article Collecting Vulnerable Source Code from Open-Source Repositories for Dataset Generation Razvan Raducu * , Gonzalo Esteban , Francisco J. Rodríguez Lera and Camino Fernández Grupo de Robótica, Universidad de León. Avenida Jesuitas, s/n, 24007 León, Spain; [email protected] (G.E.); [email protected] (F.J.R.L.); [email protected] (C.F.) * Correspondence: [email protected] Received:29 December 2019; Accepted: 7 February 2020; Published: 13 February 2020 Abstract: Different Machine Learning techniques to detect software vulnerabilities have emerged in scientific and industrial scenarios. Different actors in these scenarios aim to develop algorithms for predicting security threats without requiring human intervention. However, these algorithms require data-driven engines based on the processing of huge amounts of data, known as datasets. This paper introduces the SonarCloud Vulnerable Code Prospector for C (SVCP4C). This tool aims to collect vulnerable source code from open source repositories linked to SonarCloud, an online tool that performs static analysis and tags the potentially vulnerable code. The tool provides a set of tagged files suitable for extracting features and creating training datasets for Machine Learning algorithms. This study presents a descriptive analysis of these files and overviews current status of C vulnerabilities, specifically buffer overflow, in the reviewed public repositories. Keywords: vulnerability; sonarcloud; bot; source code; repository; buffer overflow 1. Introduction In November 1988 the Internet suffered what is publicly known as “the first successful buffer overflow exploitation”. The exploit took advantage of the absence of buffer range-checking in one of the functions implemented in the fingerd daemon [1,2]. Even though it is considered to be the first exploited buffer overflow, different researchers had been working on buffer overflow for years.
    [Show full text]
  • Dynamic Operator Overloading in a Statically Typed Language Olivier L
    Dynamic Operator Overloading in a Statically Typed Language Olivier L. Clerc and Felix O. Friedrich Computer Systems Institute, ETH Z¨urich, Switzerland [email protected], [email protected] October 31, 2011 Abstract Dynamic operator overloading provides a means to declare operators that are dispatched according to the runtime types of the operands. It allows to formulate abstract algorithms operating on user-defined data types using an algebraic notation, as it is typically found in mathematical languages. We present the design and implementation of a dynamic operator over- loading mechanism in a statically-typed object-oriented programming lan- guage. Our approach allows operator declarations to be loaded dynam- ically into a running system, at any time. We provide semantical rules that not only ensure compile-time type safety, but also facilitate the im- plementation. The spatial requirements of our approach scale well with a large number of types, because we use an adaptive runtime system that only stores dispatch information for type combinations that were encoun- tered previously at runtime. On average, dispatching can be performed in constant time. 1 Introduction Almost all programming languages have a built-in set of operators, such as +, -, * or /, that perform primitive arithmetic operations on basic data types. Operator overloading is a feature that allows the programmer to redefine the semantics of such operators in the context of custom data types. For that purpose, a set of operator implementations distinguished by their signatures has to be declared. Accordingly, each operator call on one or more custom-typed arguments will be dispatched to one of the implementations whose signature matches the operator's name and actual operand types.
    [Show full text]
  • RICH: Automatically Protecting Against Integer-Based Vulnerabilities
    RICH: Automatically Protecting Against Integer-Based Vulnerabilities David Brumley, Tzi-cker Chiueh, Robert Johnson [email protected], [email protected], [email protected] Huijia Lin, Dawn Song [email protected], [email protected] Abstract against integer-based attacks. Integer bugs appear because programmers do not antici- We present the design and implementation of RICH pate the semantics of C operations. The C99 standard [16] (Run-time Integer CHecking), a tool for efficiently detecting defines about a dozen rules governinghow integer types can integer-based attacks against C programs at run time. C be cast or promoted. The standard allows several common integer bugs, a popular avenue of attack and frequent pro- cases, such as many types of down-casting, to be compiler- gramming error [1–15], occur when a variable value goes implementation specific. In addition, the written rules are out of the range of the machine word used to materialize it, not accompanied by an unambiguous set of formal rules, e.g. when assigning a large 32-bit int to a 16-bit short. making it difficult for a programmer to verify that he un- We show that safe and unsafe integer operations in C can derstands C99 correctly. Integer bugs are not exclusive to be captured by well-known sub-typing theory. The RICH C. Similar languages such as C++, and even type-safe lan- compiler extension compiles C programs to object code that guages such as Java and OCaml, do not raise exceptions on monitors its own execution to detect integer-based attacks.
    [Show full text]
  • Secure Coding Frameworks for the Development of Safe, Secure and Reliable Code
    Building Cybersecurity from the Ground Up Secure Coding Frameworks For the Development of Safe, Secure and Reliable Code Tim Kertis October 2015 The 27 th Annual IEEE Software Technology Conference Copyright © 2015 Raytheon Company. All rights reserved. Customer Success Is Our Mission is a registered trademark of Raytheon Company. Who Am I? Tim Kertis, Software Engineer/Software Architect Chief Software Architect, Raytheon IIS, Indianapolis Master of Science, Computer & Information Science, Purdue Software Architecture Professional through the Software Engineering Institute (SEI), Carnegie-Mellon University (CMU) 30 years of diverse Software Engineering Experience Advocate for Secure Coding Frameworks (SCFs) Author of the JAVA Secure Coding Framework (JSCF) Inventor of Cybersecurity thru Lexical And Symbolic Proxy (CLaSP) technology (patent pending) Secure Coding Frameworks 10/22/2015 2 Top 5 Cybersecurity Concerns … 1 - Application According to the 2015 ISC(2) Vulnerabilities Global Information Security 2 - Malware Workforce Study (Paresh 3 - Configuration Mistakes Rathod) 4 - Mobile Devices 5 - Hackers Secure Coding Frameworks 10/22/2015 3 Worldwide Market Indicators 2014 … Number of Software Total Cost of Cyber Crime: Developers: $500B (McCafee) 18,000,000+ (www.infoq.com) Cost of Cyber Incidents: Number of Java Software Low $1.6M Developers: Average $12.7M 9,000,000+ (www.infoq.com) High $61.0M (Ponemon Institute) Software with Vulnerabilities: 96% (www.cenzic.com) Secure Coding Frameworks 10/22/2015 4 Research
    [Show full text]
  • Integer Overflow
    Lecture 05 – Integer overflow Stephen Checkoway University of Illinois at Chicago Unsafe functions in libc • strcpy • strcat • gets • scanf family (fscanf, sscanf, etc.) (rare) • printf family (more about these later) • memcpy (need to control two of the three parameters) • memmove (same as memcpy) Replacements • Not actually safe; doesn’t do what you think • strncpy • strncat • Available on Windows in C11 Annex K (the optional part of C11) • strcpy_s • strcat_s • BSD-derived, moderately widely available, including Linux kernel but not glibc • strlcpy • strlcat Buffer overflow vulnerability-finding strategy 1. Look for the use of unsafe functions 2. Trace attacker-controlled input to these functions Real-world examples from my own research • Voting machine: SeQuoia AVC Advantage • About a dozen uses of strcpy, most checked the length first • One did not. It appeared in infreQuently used code • Configuration file with fixed-width fields containing NUL-terminated strings, one of which was strcpy’d to the stack • Remote compromise of cars • Lots of strcpy of attacker-controlled Bluetooth data, first one examined was vulnerable • memcpy of attacker-controlled data from cellular modem Reminder: Think like an attacker • I skimmed some source code for a client/server protocol • The server code was full of trivial buffer overflows resulting from the attacker not following the protocol • I told the developer about the issue, but he wasn’t concerned because the client software he wrote wouldn’t send too much data • Most people don’t think like attackers. Three flavors of integer overflows 1. Truncation: Assigning larger types to smaller types int i = 0x12345678; short s = i; char c = i; Truncation example struct s { int main(int argc, char *argv[]) { unsigned short len; size_t len = strlen(argv[0]); char buf[]; }; struct s *p = malloc(len + 3); p->len = len; void foo(struct s *p) { strcpy(p->buf, argv[0]); char buffer[100]; if (p->len < sizeof buffer) foo(p); strcpy(buffer, p->buf); return 0; // Use buffer } } Three flavors of integer overflows 2.
    [Show full text]
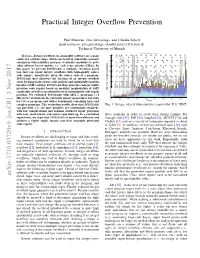
  • Practical Integer Overflow Prevention
    Practical Integer Overflow Prevention Paul Muntean, Jens Grossklags, and Claudia Eckert {paul.muntean, jens.grossklags, claudia.eckert}@in.tum.de Technical University of Munich Memory error vulnerabilities categorized 160 Abstract—Integer overflows in commodity software are a main Other Format source for software bugs, which can result in exploitable memory Pointer 140 Integer Heap corruption vulnerabilities and may eventually contribute to pow- Stack erful software based exploits, i.e., code reuse attacks (CRAs). In 120 this paper, we present INTGUARD, a symbolic execution based tool that can repair integer overflows with high-quality source 100 code repairs. Specifically, given the source code of a program, 80 INTGUARD first discovers the location of an integer overflow error by using static source code analysis and satisfiability modulo 60 theories (SMT) solving. INTGUARD then generates integer multi- precision code repairs based on modular manipulation of SMT 40 Number of VulnerabilitiesNumber of constraints as well as an extensible set of customizable code repair 20 patterns. We evaluated INTGUARD with 2052 C programs (≈1 0 Mil. LOC) available in the currently largest open-source test suite 2000 2002 2004 2006 2008 2010 2012 2014 2016 for C/C++ programs and with a benchmark containing large and Year complex programs. The evaluation results show that INTGUARD Fig. 1: Integer related vulnerabilities reported by U.S. NIST. can precisely (i.e., no false positives are accidentally repaired), with low computational and runtime overhead repair programs with very small binary and source code blow-up. In a controlled flows statically in order to avoid them during runtime. For experiment, we show that INTGUARD is more time-effective and example, Sift [35], TAP [56], SoupInt [63], AIC/CIT [74], and achieves a higher repair success rate than manually generated CIntFix [11] rely on a variety of techniques depicted in detail code repairs.
    [Show full text]
  • Ada for the C++ Or Java Developer
    Quentin Ochem Ada for the C++ or Java Developer Release 1.0 Courtesy of July 23, 2013 This work is licensed under a Creative Commons Attribution- NonCommercial-ShareAlike 3.0 Unported License. CONTENTS 1 Preface 1 2 Basics 3 3 Compilation Unit Structure 5 4 Statements, Declarations, and Control Structures 7 4.1 Statements and Declarations ....................................... 7 4.2 Conditions ................................................ 9 4.3 Loops ................................................... 10 5 Type System 13 5.1 Strong Typing .............................................. 13 5.2 Language-Defined Types ......................................... 14 5.3 Application-Defined Types ........................................ 14 5.4 Type Ranges ............................................... 16 5.5 Generalized Type Contracts: Subtype Predicates ............................ 17 5.6 Attributes ................................................. 17 5.7 Arrays and Strings ............................................ 18 5.8 Heterogeneous Data Structures ..................................... 21 5.9 Pointers .................................................. 22 6 Functions and Procedures 25 6.1 General Form ............................................... 25 6.2 Overloading ............................................... 26 6.3 Subprogram Contracts .......................................... 27 7 Packages 29 7.1 Declaration Protection .......................................... 29 7.2 Hierarchical Packages .........................................
    [Show full text]
  • Security Analysis Methods on Ethereum Smart Contract Vulnerabilities — a Survey
    1 Security Analysis Methods on Ethereum Smart Contract Vulnerabilities — A Survey Purathani Praitheeshan?, Lei Pan?, Jiangshan Yuy, Joseph Liuy, and Robin Doss? Abstract—Smart contracts are software programs featuring user [4]. In consequence of these issues of the traditional both traditional applications and distributed data storage on financial systems, the technology advances in peer to peer blockchains. Ethereum is a prominent blockchain platform with network and decentralized data management were headed up the support of smart contracts. The smart contracts act as autonomous agents in critical decentralized applications and as the way of mitigation. In recent years, the blockchain hold a significant amount of cryptocurrency to perform trusted technology is being the prominent mechanism which uses transactions and agreements. Millions of dollars as part of the distributed ledger technology (DLT) to implement digitalized assets held by the smart contracts were stolen or frozen through and decentralized public ledger to keep all cryptocurrency the notorious attacks just between 2016 and 2018, such as the transactions [1], [5], [6], [7], [8]. Blockchain is a public DAO attack, Parity Multi-Sig Wallet attack, and the integer underflow/overflow attacks. These attacks were caused by a electronic ledger equivalent to a distributed database. It can combination of technical flaws in designing and implementing be openly shared among the disparate users to create an software codes. However, many more vulnerabilities of less sever- immutable record of their transactions [7], [9], [10], [11], ity are to be discovered because of the scripting natures of the [12], [13]. Since all the committed records and transactions Solidity language and the non-updateable feature of blockchains.
    [Show full text]
  • Security Coding Module Integer Error – “You Can’T Count That High” – CS1
    Security Coding Module Integer Error – “You Can’t Count That High” – CS1 Summary: Integer values that are too large or too small may fall outside the allowable range for their data type, leading to undefined behavior that can both reduce the robustness of your code and lead to security vulnerabilities. Description: Declaring a variable as type int allocates a fixed amount of space in memory. Most languages include several integer types, including short, int, long, etc. , to allow for less or more storage. The amount of space allocated limits the range of values that can be stored. For example, a 32-bit int variable can hold values from -231 through 231-1. Input or mathematical operations such as addition, subtraction, and multiplication may lead to values that are outside of this range. This results in an integer error or overflow, which causes undefined behavior and the resulting value will likely not be what the programmer intended. Integer overflow is a common cause of software errors and vulnerabilities. Risk – How Can It Happen? An integer error can lead to unexpected behavior or may be exploited to cause a program crash, corrupt data, or allow the execution of malicious software. Example of Occurrence: 1. There is a Facebook group called “If this group reaches 4,294,967,296 it might cause an integer overflow.” This value is the largest number that can fit in a 32 bit unsigned integer. If the number of members of the group exceeded this number, it might cause an overflow. Whether it will cause an overflow or not depends upon how Facebook is implemented and which language is used – they might use data types that can hold larger numbers.
    [Show full text]
  • Teaching Security Stealthily
    Education Editors: Matt Bishop, [email protected] Cynthia Irvine, [email protected] Teaching Security Stealthily Matt Bishop University of California, Davis Many people and institutions are considering how to make students who aren’t taking computer security classes aware of the issues and make them think about how to improve the state of software and systems. Elementary programming classes teach problem-solving skills as well as programming-language syntax and semantics. Database classes focus on the theory and practice of storing, viewing, and extracting data. Algorithm classes emphasize algorithm design and analysis. Their teaching objectives might not even mention security. A class’s topic constrains its content, and any information or practice of security is strictly incidental to the students’ understanding and internalization of the material relevant to the topic. However, information assurance and computer security are cross-disciplinary topics. They arise in all computer science disciplines. Thus, their material can and should be integrated into existing classes—but doing so presents a conundrum. Already, computer science classes’ curriculum covers more material than can be comfortably taught in each class. So, rather than remove material about the class’s primary topic, classes can introduce security-related concepts in homework exercises, thereby emphasizing those concepts in the context of that topic. Here, I present four exercises: one from a class introducing nonmajors to computers and programming, and three from a beginning programming class for majors. We focus on introductory classes because they form the basis for students’ computing experiences. Introducing concepts of information assurance and computer security early makes the students more aware of these issues.
    [Show full text]
  • Multimethods
    11-A1568 01/23/2001 12:39 PM Page 263 11 Multimethods This chapter defines, discusses, and implements multimethods in the context of Cϩϩ . The Cϩϩ virtual function mechanism allows dispatching a call depending on the dynamic type of one object. The multimethods feature allows dispatching a function call depending on the types of multiple objects. A universally good implementation requires language support, which is the route that languages such as CLOS, ML, Haskell, and Dylan have taken. Cϩϩ lacks such support, so its emulation is left to library writers. This chapter discusses some typical solutions and some generic implementations of each. The solutions feature various trade-offs in terms of speed, flexibility, and dependency management. To describe the technique of dispatching a function call depending on mul- tiple objects, this book uses the terms multimethod (borrowed from CLOS) and multiple dis- patch. A particularization of multiple dispatch for two objects is known as double dispatch. Implementing multimethods is a problem as fascinating as dreaded, one that has stolen lots of hours of good, healthy sleep from designers and programmers.1 The topics of this chapter include • Defining multimethods • Identifying situations in which the need for multiobject polymorphism appears • Discussing and implementing three double dispatchers that foster different trade-offs • Enhancing double-dispatch engines After reading this chapter, you will have a firm grasp of the typical situations for which multimethods are the way to go. In addition, you will be able to use and extend several ro- bust generic components implementing multimethods, provided by Loki. This chapter limits discussion to multimethods for two objects (double dispatch).
    [Show full text]