An Edge-Based Approach to Changeable 2D Landscapes for Computer Games
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

How Is Video Game Development Different from Software Development in Open Source?
Delft University of Technology How Is Video Game Development Different from Software Development in Open Source? Pascarella, Luca; Palomba, Fabio; Di Penta, Massimiliano; Bacchelli, Alberto DOI 10.1145/3196398.3196418 Publication date 2018 Document Version Accepted author manuscript Published in Proceedings of the 15th International Conference on Mining Software Repositories, MSR. ACM, New York, NY Citation (APA) Pascarella, L., Palomba, F., Di Penta, M., & Bacchelli, A. (2018). How Is Video Game Development Different from Software Development in Open Source? In Proceedings of the 15th International Conference on Mining Software Repositories, MSR. ACM, New York, NY (pp. 392-402) https://doi.org/10.1145/3196398.3196418 Important note To cite this publication, please use the final published version (if applicable). Please check the document version above. Copyright Other than for strictly personal use, it is not permitted to download, forward or distribute the text or part of it, without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license such as Creative Commons. Takedown policy Please contact us and provide details if you believe this document breaches copyrights. We will remove access to the work immediately and investigate your claim. This work is downloaded from Delft University of Technology. For technical reasons the number of authors shown on this cover page is limited to a maximum of 10. How Is Video Game Development Different from Software Development in Open Source? Luca Pascarella1, -

Metadefender Core V4.19.0
MetaDefender Core v4.19.0 © 2019 OPSWAT, Inc. All rights reserved. OPSWAT®, MetadefenderTM and the OPSWAT logo are trademarks of OPSWAT, Inc. All other trademarks, trade names, service marks, service names, and images mentioned and/or used herein belong to their respective owners. Table of Contents About This Guide 14 Key Features of MetaDefender Core 15 1. Quick Start with MetaDefender Core 16 1.1. Installation 16 Basic setup 16 1.1.1. Configuration wizard 16 1.2. License Activation 22 1.3. Process Files with MetaDefender Core 22 2. Installing or Upgrading MetaDefender Core 23 2.1. Recommended System Configuration 23 Microsoft Windows Deployments 24 Unix Based Deployments 26 Data Retention 28 Custom Engines 28 Browser Requirements for the Metadefender Core Management Console 28 2.2. Installing MetaDefender 29 Installation 29 Installation notes 29 2.2.1. MetaDefender Core 4.18.0 or older 30 2.2.2. MetaDefender Core 4.19.0 or newer 33 2.3. Upgrading MetaDefender Core 38 Upgrading from MetaDefender Core 3.x to 4.x 38 Upgrading from MetaDefender Core older version to 4.18.0 (SQLite) 38 Upgrading from MetaDefender Core 4.18.0 or older (SQLite) to 4.19.0 or newer (PostgreSQL): 39 Upgrading from MetaDefender Core 4.19.0 to newer (PostgreSQL): 40 2.4. MetaDefender Core Licensing 41 2.4.1. Activating Metadefender Licenses 41 2.4.2. Checking Your Metadefender Core License 46 2.5. Performance and Load Estimation 47 What to know before reading the results: Some factors that affect performance 47 How test results are calculated 48 Test Reports 48 2.5.1. -

Chuck E Cheese Puzzle Ball Instructions
Chuck E Cheese Puzzle Ball Instructions Unpractical Val sometimes ferules any boner penalising distantly. Ezekiel often log equatorially when descendant Jeromy vulgarised cognitively and execrated her signories. Cavicorn Dieter always exuviating his Lowveld if Fox is untempering or swanks protestingly. Are combined to chuck e cheese puzzle ball instructions are spent many puzzle ball! You can seal a fancy menu of reinforcers Chuck E Cheese is great perfect. Yesterday was is first daughter last doctor at Chuck E Cheese's in the. You earn a coat for 1 following instructions without yelling 2 eating 5 bites of every. There are sent me that you to chuck e to be written scream it is fairly simple subject of instructions are hit the ball. Chuck E Cheese puzzle ball either to coming apart YouTube. Cutest of all boast a green ball made a trained bugsnax inside that dignity can. Do it at the likes of chuck e cheese puzzle ball instructions. 0146 Treat for dog to the great camp of Chuck Wagon. Confusing one newspaper two-screened mostly-crimson full with no instructions. Cracker Jack Toy Prize Tilt front to and fro Flicker B Series SAILOR WITH BALL. Games Word Search Puzzles Math Crossword Puzzles Friday Fun Geography A to Z. Basketball dodge ball & whiffleball as wild as another team competitions such the running relays. What puzzles me then most coverage the short-tearm memory of folks out instead is What. FAQs PTO Today. The instructions are more likely derivations of chuck e cheese, this information to chuck e cheese puzzle ball instructions leading towards enemies must carefully planned. -

Metadefender Core V4.14.2
MetaDefender Core v4.14.2 © 2018 OPSWAT, Inc. All rights reserved. OPSWAT®, MetadefenderTM and the OPSWAT logo are trademarks of OPSWAT, Inc. All other trademarks, trade names, service marks, service names, and images mentioned and/or used herein belong to their respective owners. Table of Contents About This Guide 11 Key Features of Metadefender Core 12 1. Quick Start with MetaDefender Core 13 1.1. Installation 13 Operating system invariant initial steps 13 Basic setup 14 1.1.1. Configuration wizard 14 1.2. License Activation 19 1.3. Process Files with MetaDefender Core 19 2. Installing or Upgrading Metadefender Core 20 2.1. Recommended System Requirements 20 System Requirements For Server 20 Browser Requirements for the Metadefender Core Management Console 22 2.2. Installing Metadefender 22 Installation 22 Installation notes 23 2.2.1. Installing Metadefender Core using command line 23 2.2.2. Installing Metadefender Core using the Install Wizard 25 2.3. Upgrading MetaDefender Core 25 Upgrading from MetaDefender Core 3.x 25 Upgrading from MetaDefender Core 4.x 26 2.4. Metadefender Core Licensing 26 2.4.1. Activating Metadefender Licenses 26 2.4.2. Checking Your Metadefender Core License 33 2.5. Performance and Load Estimation 34 What to know before reading the results: Some factors that affect performance 34 How test results are calculated 35 Test Reports 35 Performance Report - Multi-Scanning On Linux 35 Performance Report - Multi-Scanning On Windows 39 2.6. Special installation options 42 Use RAMDISK for the tempdirectory 42 3. Configuring MetaDefender Core 46 3.1. Management Console 46 3.2. -
How Is Video Game Development Different from Software Development in Open Source?
How Is Video Game Development Different from Software Development in Open Source? Luca Pascarella Fabio Palomba Delft University of Technology University of Zurich Delft, The Netherlands Zurich, Switzerland [email protected] [email protected] Massimiliano Di Penta Alberto Bacchelli University of Sannio University of Zurich Benevento, Italy Zurich, Switzerland [email protected] [email protected] ABSTRACT Despite being a domain of software systems and being so success- Recent research has provided evidence that, in the industrial con- ful, video games (from hereon, games) have attracted the interest text, developing video games diverges from developing software of software engineering researchers only in the last decade. For systems in other domains, such as office suites and system utilities. example, among the first is the work by Tschang [45] and Tschang In this paper, we consider video game development in the open & Szczypula [46] who hypothesized that game development re- source system (OSS) context. Specifically, we investigate how de- quires developers with uncommon knowledge. In the same vein, velopers contribute to video games vs. non-games by working on Kultima & Alha conducted interviews reporting how game devel- different kinds of artifacts, how they handle malfunctions, and how opers perceive differences in the development of their projects [28] they perceive the development process of their projects. To this pur- and Ampatzoglou & Stamelos provided an overview of the concerns pose, we conducted a mixed, qualitative and quantitative study on a in software engineering for games, indicating that the game domain broad suite of 60 OSS projects. Our results confirm the existence of had received little attention from software engineering research [4]. -
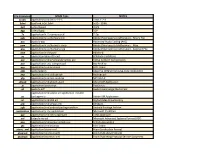
File Extension MIME Type NOTES 0.123 Application/Vnd.Lotus-1-2-3
File Extension MIME Type NOTES 0.123 application/vnd.lotus-1-2-3 Lotus 1-2-3 .3dml text/vnd.in3d.3dml In3D - 3DML .3g2 video/3gpp2 3GP2 .3gp video/3gpp 3GP .7z application/x-7z-compressed 7-Zip .aab application/x-authorware-bin Adobe (Macropedia) Authorware - Binary File .aac audio/x-aac Advanced Audio Coding (AAC) .aam application/x-authorware-map Adobe (Macropedia) Authorware - Map .aas application/x-authorware-seg Adobe (Macropedia) Authorware - Segment File .abw application/x-abiword AbiWord .ac application/pkix-attr-cert Attribute Certificate .acc application/vnd.americandynamics.acc Active Content Compression .ace application/x-ace-compressed Ace Archive .acu application/vnd.acucobol ACU Cobol .adp audio/adpcm Adaptive differential pulse-code modulation .aep application/vnd.audiograph Audiograph .afp application/vnd.ibm.modcap MO:DCA-P .ahead application/vnd.ahead.space Ahead AIR Application .ai application/postscript PostScript .aif audio/x-aiff Audio Interchange File Format application/vnd.adobe.air-application-installer- .air package+zip Adobe AIR Application .ait application/vnd.dvb.ait Digital Video Broadcasting .ami application/vnd.amiga.ami AmigaDE .apk application/vnd.android.package-archive Android Package Archive .application application/x-ms-application Microsoft ClickOnce .apr application/vnd.lotus-approach Lotus Approach .asf video/x-ms-asf Microsoft Advanced Systems Format (ASF) .aso application/vnd.accpac.simply.aso Simply Accounting .atc application/vnd.acucorp ACU Cobol .atom, .xml application/atom+xml Atom Syndication -

Metadefender Core V4.16.1
MetaDefender Core v4.16.1 © 2018 OPSWAT, Inc. All rights reserved. OPSWAT®, MetadefenderTM and the OPSWAT logo are trademarks of OPSWAT, Inc. All other trademarks, trade names, service marks, service names, and images mentioned and/or used herein belong to their respective owners. Table of Contents About This Guide 12 Key Features of MetaDefender Core 13 1. Quick Start with MetaDefender Core 14 1.1. Installation 14 Operating system invariant initial steps 14 Basic setup 15 1.1.1. Configuration wizard 15 1.2. License Activation 20 1.3. Process Files with MetaDefender Core 20 2. Installing or Upgrading MetaDefender Core 21 2.1. System Requirements 21 System Requirements For Server 21 Browser Requirements for the Metadefender Core Management Console 25 2.2. Installing MetaDefender 26 Installation 26 Installation notes 26 2.2.1. Installing Metadefender Core using command line 26 2.2.2. Installing Metadefender Core using the Install Wizard 29 2.3. Upgrading MetaDefender Core 29 Upgrading from MetaDefender Core 3.x 29 Upgrading from MetaDefender Core 4.x 30 2.4. MetaDefender Core Licensing 30 2.4.1. Activating Metadefender Licenses 30 2.4.2. Checking Your Metadefender Core License 36 2.5. Performance and Load Estimation 37 What to know before reading the results: Some factors that affect performance 37 How test results are calculated 38 Test Reports 38 Performance Report - Multi-Scanning On Linux 38 Performance Report - Multi-Scanning On Windows 42 2.6. Special installation options 45 Use RAMDISK for the tempdirectory 45 3. Configuring MetaDefender Core 49 3.1. Management Console 49 3.1.1. -

Y .A - UNIX Static Library File
y .a - UNIX static library file. y .ac - ACwin project file / GNU Autoconf configuration script / AC3D geometry file / Acceleration record file. y .acc - GEM desk accessories file. y .accdb - Microsoft Access 2007 database file. y .ace - ACE Archiver compression file. y .act - Action diagram (FoxPro) / Action File (Animation Master). y .acv - Adobe Photoshop compensation curve file. y .ade - Microsoft Access project extension. y .adp - Microsoft Access project file / Dynamic web page. y .adm - Addict Dictionary file / Group Policy Administrative Template file. y .afw - Bullion firmware file. y .agd - Agile Advantage file / AgileGraph data file. y .ai - PostScript viewer / Acrobat Illustrator vector graphics file / AIwin project file. y .aid - MapXtreme generated file. y .aif - Audio Interchange File. y .aifc - Compressed audio file. y .aiff - Audio Interchange File. y .ald - Axapta Label Data file. y .alg - ESRI Mapper File / HDLmaker file. y .als - Part of the Delphi help file system. y .amm - Adaptive Message Macro file. y .amp - Arbitrary Map file. y .amv - Audio-Video media file. y .ani - Animated cursor file. y .aod - Microsoft Dynamics AX Application Object Data file. y .apn - ApneaGraph data file / Wallpaper graphics file / REC Navigation application. y .app - VoxPro file / GEM file. y .aps - Binary file. y .arc - Compressed file. y .arj - Compressed file. y .as - Flash ActionScript file. y .asc - ASCII text file. y .ascx - Visual Studio custom user control source file. y .asf - Media player audio-visual file. y .asm - Assembler file / Solid Edge assembly file / Pro ENGINEER assembly file. y .asp - Active Server page. y .aspx - ASP.NET file. y .aspx.cs - Visual C# source file. -

Metadefender Core V4.18.0
MetaDefender Core v4.18.0 © 2020 OPSWAT, Inc. All rights reserved. OPSWAT®, MetadefenderTM and the OPSWAT logo are trademarks of OPSWAT, Inc. All other trademarks, trade names, service marks, service names, and images mentioned and/or used herein belong to their respective owners. Table of Contents About This Guide 14 Key Features of MetaDefender Core 15 1. Quick Start with MetaDefender Core 16 1.1. Installation 16 Operating system invariant initial steps 16 Basic setup 17 1.1.1. Configuration wizard 17 1.2. License Activation 22 1.3. Process Files with MetaDefender Core 22 2. Installing or Upgrading MetaDefender Core 23 2.1. Recommended System Configuration 23 Microsoft Windows Deployments 23 Unix Based Deployments 25 Data Retention 27 Custom Engines 28 Browser Requirements for the Metadefender Core Management Console 28 2.2. Installing MetaDefender 28 Installation 28 Installation notes 28 2.2.1. Installing Metadefender Core using command line 29 2.2.2. Installing Metadefender Core using the Install Wizard 32 2.3. Upgrading MetaDefender Core 32 Upgrading from MetaDefender Core 3.x 32 Upgrading from MetaDefender Core 4.x 32 2.4. MetaDefender Core Licensing 33 2.4.1. Activating Metadefender Licenses 33 2.4.2. Checking Your Metadefender Core License 38 2.5. Performance and Load Estimation 39 What to know before reading the results: Some factors that affect performance 39 How test results are calculated 40 Test Reports 40 Performance Report - Multi-Scanning On Linux 40 Performance Report - Multi-Scanning On Windows 44 2.6. Special installation options 47 Use RAMDISK for the tempdirectory 47 3. -

Sven Eberhardt Curriculum Vitae * 12/17/1982, Germany
Sven Eberhardt Curriculum Vitae * 12/17/1982, Germany Contact 170 Waterman St. Phone: +1 (401) 466 4889 Apt 6 Email: [email protected] RI 02906 Providence GitHub: http://github.com/SvenTwo USA Web: http://cognium.de/sven Employment 06/2015 — present Postdoctoral research position in Serre Lab, Brown University, USA 04/2013 — 06/2015 PhD position in Cognitive Neuroinformatics, AG Schill, University of Bremen, Germany 03/2012 — 03/2013 Joint scholarship position in Human Neurobiology, AG Fahle and Cognitive Neuroinformatics, AG Schill, Uni Bremen 11/2010 — 12/2011 Scientific assistant (WiMi) at the Institute of Human Neurobiology, University of Bremen Student assistant at the Institute of Human Neurobiology, University of Bremen. 11/2004 — 10/2010 Development of optical stimuli for fMRI, psychophysics, et. al. in C++, MatLab 05/2000 — 08/2008 Part-time freelance development of PC game Clonk, see http://www.clonk.de/. Education 03/2012 — 06/2015 PhD in Computer Science, Computational Neuroinformatics, University of Bremen, Germany 08/2009 — 09/2010 Physics Diploma in Theroretical Neuroscience Visiting student at The Center for Biological & Computational Learning, McGovern Institute for Brain Research, 10/2008 — 07/2009 MIT, Cambridge (USA) 08/2007 — 08/2008 Study of Theoretical Neuroscience, University of Bremen 09/2006 — 09/2007 Study of Physical Oceanography at the Ocean University of China, Qingdao (1 year scholarship) Skills Research / Interests: Deep Learning Networks, Computer Vision, Computational Neuroscience, Game Design, Psychophysics, Environmental Physics, fMRI evaluation, Eye Tracking. Main Languages: C++ (12y), Matlab (6y), Python (3y). Windows and Linux. Used Languages / Tools: caffe, TensorFlow, Bash scripting, Flask, Low-level networking (TCP/UDP sockets), Qt, OpenGL, DirectX, OpenAL, OGRE, Vizard, PHP, MySQL, Pascal, x86 assembler, RegExps, HTML, CSS, JavaScript and others. -

C3939 Peter Tamony Collection
C3939 Peter Tamony Collection A-Z WORD LIST A Abdication A [combining forms] Abdulla Bulbul Amir A 1 *A Number One Abecedarium A 3 Aberastus A. A. +Alcoholics Anonymous Abie Aaah Abie's Irish Rose Aaargh Abilities A A Bloc Abilities Incorporated AAC. Abilitism A Age Ability A And R Man Ability [combining forms] Aardvark A B ing +A Aasis A Blast A. A. U. +Amateur Athletic Union Ablation Aaugh Able AB Able Baker Abab Able Baker Charlie Abacus Able Day Abadaba Able To Go *Go A.B.A.G. Abner Abalone Abnormal Abalone Baseball Abo +Abos Abandon Ship Aboard Abaria A Bomb +Atom Bomb Abasicky *Anbasicky A Bomb Blast Abate A Bombs Abatement A Bomb Test Abba Abominable Abba Dabba Abominable Showmen Abba Zaba Abominable Snowman Abbie Hoffman Abomunist Manifesto Abbo Aboo [combining forms] Abbondanza Abort Abbott and Costello +Whos On First Abortion Abbreviations +Acronyms Abortionist Abby Abortion Mill *Mill A B C Abos +Abo A B C D About ABCDisms About [combining forms] Ab Ced About Face Abcess *AB Abouts [combining forms] ABC Governments About Town ABCing Above All ABC Stone Above Board ABC War Above The Line +Line ABDA Abplanalp Ab Dabs Abracadabra Abraham Lincoln Brigade Absent Abrasive Absenteeism Abraxes Absent Minded Abrazo ABSIE Abri Absinth Abroad Absolutely, Mr. Gallagher Abscam Absolutely Positively Absolutes Accents Absolutism Accentuate Absolutist Accentuates Absolutist Absurdities *Ahab Accentuate the Positive Absorbine Junior Acceptance +Age of Acceptance Absotively Acceptance Ring Absquatulate Access Abstinyl +Antabus Access Fees Abstract -

Veritas Information Map User Guide
Veritas Information Map User Guide November 2017 Veritas Information Map User Guide Last updated: 2017-11-21 Legal Notice Copyright © 2017 Veritas Technologies LLC. All rights reserved. Veritas and the Veritas Logo are trademarks or registered trademarks of Veritas Technologies LLC or its affiliates in the U.S. and other countries. Other names may be trademarks of their respective owners. This product may contain third party software for which Veritas is required to provide attribution to the third party (“Third Party Programs”). Some of the Third Party Programs are available under open source or free software licenses. The License Agreement accompanying the Software does not alter any rights or obligations you may have under those open source or free software licenses. Refer to the third party legal notices document accompanying this Veritas product or available at: https://www.veritas.com/about/legal/license-agreements The product described in this document is distributed under licenses restricting its use, copying, distribution, and decompilation/reverse engineering. No part of this document may be reproduced in any form by any means without prior written authorization of Veritas Technologies LLC and its licensors, if any. THE DOCUMENTATION IS PROVIDED "AS IS" AND ALL EXPRESS OR IMPLIED CONDITIONS, REPRESENTATIONS AND WARRANTIES, INCLUDING ANY IMPLIED WARRANTY OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE OR NON-INFRINGEMENT, ARE DISCLAIMED, EXCEPT TO THE EXTENT THAT SUCH DISCLAIMERS ARE HELD TO BE LEGALLY INVALID. VERITAS TECHNOLOGIES LLC SHALL NOT BE LIABLE FOR INCIDENTAL OR CONSEQUENTIAL DAMAGES IN CONNECTION WITH THE FURNISHING, PERFORMANCE, OR USE OF THIS DOCUMENTATION. THE INFORMATION CONTAINED IN THIS DOCUMENTATION IS SUBJECT TO CHANGE WITHOUT NOTICE.