New Empirical Equations for Calculating Sound Pressure Levels in Rooms
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

6. Units and Levels
NOISE CONTROL Units and Levels 6.1 6. UNITS AND LEVELS 6.1 LEVELS AND DECIBELS Human response to sound is roughly proportional to the logarithm of sound intensity. A logarithmic level (measured in decibels or dB), in Acoustics, Electrical Engineering, wherever, is always: Figure 6.1 Bell’s 1876 é power ù patent drawing of the 10log ê ú telephone 10 ëreference power û (dB) An increase in 1 dB is the minimum increment necessary for a noticeably louder sound. The decibel is 1/10 of a Bel, and was named by Bell Labs engineers in honor of Alexander Graham Bell, who in addition to inventing the telephone in 1876, was a speech therapist and elocution teacher. = W = −12 Sound power level: LW 101og10 Wref 10 watts Wref Sound intensity level: = I = −12 2 LI 10log10 I ref 10 watts / m I ref Sound pressure level (SPL): P 2 P = rms = rms = µ = 2 L p 10log10 2 20log10 Pref 20 Pa .00002 N / m Pref Pref Some important numbers and unit conversions: 1 Pa = SI unit for pressure = 1 N/m2 = 10µBar 1 psi = antiquated unit for the metricly challenged = 6894Pa kg ρc = characteristic impedance of air = 415 = 415 mks rayls (@20°C) s ⋅ m2 c= speed of sound in air = 343 m/sec (@20°C, 1 atm) J. S. Lamancusa Penn State 12/4/2000 NOISE CONTROL Units and Levels 6.2 How do dB’s relate to reality? Table 6.1 Sound pressure levels of various sources Sound Pressure Description of sound source Subjective Level (dB re 20 µPa) description 140 moon launch at 100m, artillery fire at gunner’s intolerable, position hazardous 120 ship’s engine room, rock concert in front and close to speakers 100 textile mill, press room with presses running, very noise punch press and wood planers at operator’s position 80 next to busy highway, shouting noisy 60 department store, restaurant, speech levels 40 quiet residential neighborhood, ambient level quiet 20 recording studio, ambient level very quiet 0 threshold of hearing for normal young people 6.2 COMBINING DECIBEL LEVELS Incoherent Sources Sound at a receiver is often the combination from two or more discrete sources. -

Sony F3 Operating Manual
4-276-626-11(1) Solid-State Memory Camcorder PMW-F3K PMW-F3L Operating Instructions Before operating the unit, please read this manual thoroughly and retain it for future reference. © 2011 Sony Corporation WARNING apparatus has been exposed to rain or moisture, does not operate normally, or has To reduce the risk of fire or electric shock, been dropped. do not expose this apparatus to rain or moisture. IMPORTANT To avoid electrical shock, do not open the The nameplate is located on the bottom. cabinet. Refer servicing to qualified personnel only. WARNING Excessive sound pressure from earphones Important Safety Instructions and headphones can cause hearing loss. In order to use this product safely, avoid • Read these instructions. prolonged listening at excessive sound • Keep these instructions. pressure levels. • Heed all warnings. • Follow all instructions. For the customers in the U.S.A. • Do not use this apparatus near water. This equipment has been tested and found to • Clean only with dry cloth. comply with the limits for a Class A digital • Do not block any ventilation openings. device, pursuant to Part 15 of the FCC Rules. Install in accordance with the These limits are designed to provide manufacturer's instructions. reasonable protection against harmful • Do not install near any heat sources such interference when the equipment is operated as radiators, heat registers, stoves, or other in a commercial environment. This apparatus (including amplifiers) that equipment generates, uses, and can radiate produce heat. radio frequency energy and, if not installed • Do not defeat the safety purpose of the and used in accordance with the instruction polarized or grounding-type plug. -

Sound Power Measurement What Is Sound, Sound Pressure and Sound Pressure Level?
www.dewesoft.com - Copyright © 2000 - 2021 Dewesoft d.o.o., all rights reserved. Sound power measurement What is Sound, Sound Pressure and Sound Pressure Level? Sound is actually a pressure wave - a vibration that propagates as a mechanical wave of pressure and displacement. Sound propagates through compressible media such as air, water, and solids as longitudinal waves and also as transverse waves in solids. The sound waves are generated by a sound source (vibrating diaphragm or a stereo speaker). The sound source creates vibrations in the surrounding medium. As the source continues to vibrate the medium, the vibrations propagate away from the source at the speed of sound and are forming the sound wave. At a fixed distance from the sound source, the pressure, velocity, and displacement of the medium vary in time. Compression Refraction Direction of travel Wavelength, λ Movement of air molecules Sound pressure Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average, or equilibrium) atmospheric pressure, caused by a sound wave. In air the sound pressure can be measured using a microphone, and in water with a hydrophone. The SI unit for sound pressure p is the pascal (symbol: Pa). 1 Sound pressure level Sound pressure level (SPL) or sound level is a logarithmic measure of the effective sound pressure of a sound relative to a reference value. It is measured in decibels (dB) above a standard reference level. The standard reference sound pressure in the air or other gases is 20 µPa, which is usually considered the threshold of human hearing (at 1 kHz). -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Lumens and Loudness: Projector Noise in a Nutshell
Lumens and loudness: Projector noise in a nutshell Jackhammers tearing up the street outside; the In this white paper, we’re going to take a closer look at projector noise: what causes neighbor’s dog barking at squirrels; the hum of it, how to measure it, and how to keep it to a minimum. the refrigerator: noise is a fixture in our daily Why do projectors make noise? lives, and projectors are no exception. Like many high-tech devices, they depend on cooling There’s more than one source of projector noise, of course, but cooling fans are by systems that remove excess heat before it can far the major offender—and there’s no way around them. Especially projector bulbs cause permanent damage, and these systems give off a lot of heat. This warmth must be continuously removed or the projector will overheat, resulting in serious damage to the system. The fans that keep air unavoidably produce noise. flowing through the projector, removing heat before it can build to dangerous levels, make noise. Fans can’t help but make noise: they are designed to move air, and the movement of air is what makes sound. How much sound they make depends on their construction: the angle of the blades, their size, number and spacing, their surface quality, and the fan’s rotational speed. Moreover, for projector manufacturers it’s also key not to place a fan too close to an air vent or any kind of mesh, or they’ll end up with the siren effect: very annoying high-frequency, pure-tone noise caused by the sudden interruption of the air flow by the vent bars or the mesh wires. -

Solid-State Memory Camcorder
4-425-717-13(3) Solid-State Memory Camcorder PMW-200 PMW-100 Operating Instructions Before operating the unit, please read this manual thoroughly and retain it for future reference. © 2012 Sony Corporation WARNING • Refer all servicing to qualified service personnel. Servicing is required when the To reduce the risk of fire or electric shock, apparatus has been damaged in any way, do not expose this apparatus to rain or such as power-supply cord or plug is moisture. damaged, liquid has been spilled or objects To avoid electrical shock, do not open the have fallen into the apparatus, the apparatus cabinet. Refer servicing to qualified has been exposed to rain or moisture, does personnel only. not operate normally, or has been dropped. WARNING Do not install the appliance in a confined When installing the unit, incorporate a readily space, such as book case or built-in cabinet. accessible disconnect device in the fixed wiring, or connect the power plug to an easily IMPORTANT accessible socket-outlet near the unit. If a fault The nameplate is located on the bottom. should occur during operation of the unit, WARNING operate the disconnect device to switch the Excessive sound pressure from earphones power supply off, or disconnect the power plug. and headphones can cause hearing loss. In order to use this product safely, avoid Important Safety Instructions prolonged listening at excessive sound • Read these instructions. pressure levels. • Keep these instructions. • Heed all warnings. For the customers in the U.S.A. • Follow all instructions. This equipment has been tested and found to • Do not use this apparatus near water. -

The Human Ear Hearing, Sound Intensity and Loudness Levels
UIUC Physics 406 Acoustical Physics of Music The Human Ear Hearing, Sound Intensity and Loudness Levels We’ve been discussing the generation of sounds, so now we’ll discuss the perception of sounds. Human Senses: The astounding ~ 4 billion year evolution of living organisms on this planet, from the earliest single-cell life form(s) to the present day, with our current abilities to hear / see / smell / taste / feel / etc. – all are the result of the evolutionary forces of nature associated with “survival of the fittest” – i.e. it is evolutionarily{very} beneficial for us to be able to hear/perceive the natural sounds that do exist in the environment – it helps us to locate/find food/keep from becoming food, etc., just as vision/sight enables us to perceive objects in our 3-D environment, the ability to move /locomote through the environment enhances our ability to find food/keep from becoming food; Our sense of balance, via a stereo-pair (!) of semi-circular canals (= inertial guidance system!) helps us respond to 3-D inertial forces (e.g. gravity) and maintain our balance/avoid injury, etc. Our sense of taste & smell warn us of things that are bad to eat and/or breathe… Human Perception of Sound: * The human ear responds to disturbances/temporal variations in pressure. Amazingly sensitive! It has more than 6 orders of magnitude in dynamic range of pressure sensitivity (12 orders of magnitude in sound intensity, I p2) and 3 orders of magnitude in frequency (20 Hz – 20 KHz)! * Existence of 2 ears (stereo!) greatly enhances 3-D localization of sounds, and also the determination of pitch (i.e. -

Introduction to Noise
CHICAGO DEPARTMENT OF AVIATION INTRODUCTION TO NOISE This document provides the background reference material on the principles of noise, noise analysis, and modeling, as well as the preparation of airport noise exposure contours and how the estimates of noise impacts inside a 65 Day-Night Average Sound Level (DNL) noise contour are determined. The data is derived from a variety of sources including, but not limited to, records maintained by airport management and the Federal Aviation Administration (FAA), and mapping available from the airport, and local planning agencies. 1 SOUND AND NOISE Sound is created by a vibrating source that induces vibrations in the air. The vibration produces relatively dense and sparse alternating bands of particles of air, spreading outward from the source like ripples on a pond. Sound waves dissipate with increasing distance from the source. Sound waves can also be reflected, diffracted, refracted, or scattered. When the source stops vibrating, the sound waves disappear almost instantly and the sound ceases. Sound conveys information to listeners. It can be instructional, alarming, pleasant and relaxing, or annoying. Identical sounds can be characterized by different people or even by the same person at different times, as desirable or unwanted. Unwanted sound is commonly referred to as “noise.” Sound can be defined in terms of three components: Level (amplitude) Pitch (frequency) Duration (time pattern) 1.1 SOUND LEVEL The level of sound is measured by the difference between atmospheric pressure (without the sound) and the total pressure (with the sound). Amplitude of sound is like the relative height of the ripples caused by the stone thrown into the water. -

Lecture 1-2: Sound Pressure Level Scale
Lecture 1-2: Sound Pressure Level Scale Overview 1. Psychology of Sound. We can define sound objectively in terms of its physical form as pressure variations in a medium such as air, or we can define it subjectively in terms of the sensations generated by our hearing mechanism. Of course the sensation we perceive from a sound is linked to the physical properties of the sound wave through our hearing mechanism, whereby some aspects of the pressure variations are converted into firings in the auditory nerve. The study of how the objective physical character of sound gives rise to subjective auditory sensation is called psychoacoustics. The three dimensions of our psychological sensation of sound are called Loudness , Pitch and Timbre . 2. How can we measure the quantity of sound? The amplitude of a sound is a measure of the average variation in pressure, measured in pascals (Pa). Since the mean amplitude of a sound is zero, we need to measure amplitude either as the distance between the most negative peak and the most positive peak or in terms of the root-mean-square ( rms ) amplitude (i.e. the square root of the average squared amplitude). The power of a sound source is a measure of how much energy it radiates per second in watts (W). It turns out that the power in a sound is proportional to the square of its amplitude. The intensity of a sound is a measure of how much power can be collected per unit area in watts per square metre (Wm -2). For a sound source of constant power radiating equally in all directions, the sound intensity must fall with the square of the distance to the source (since the radiated energy is spread out through the surface of a sphere centred on the source, and the surface area of the sphere increases with the square of its radius). -
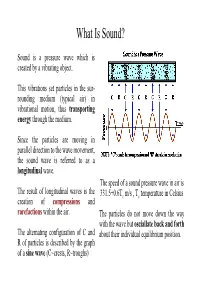
What Is Sound?
What Is Sound? Sound is a pressure wave which is created by a vibrating object. This vibrations set particles in the sur- rounding medium (typical air) in vibrational motion, thus transporting energy through the medium. Since the particles are moving in parallel direction to the wave movement, the sound wave is referred to as a longitudinal wave. The speed of a sound pressure wave in air is The result of longitudinal waves is the 331.5+0.6Tc m/s , Tc temperature in Celsius creation of compressions and rarefactions within the air. The particles do not move down the way with the wave but osciallate back and forth The alternating configuration of C and about their individual equilibrium position. R of particles is described by the graph of a sine wave (C~crests, R~troughs) Wavelength, Amplitude, Frequency of a Wave The amount of work done to generate the energy that sets the particles in motion is reflected in the degree of displacement which is measured as the amplitude of a sound. The frequency f of a wave is measured as the number of complete back-and-forth vibrations of a particle of the medium per unit of time. 1 Hertz = 1 vibration/second f = 1/Time Depending on the medium, sound travels at some speed c which defines the wavelength l: l = c/f Measuring the Intensity of Sound • The softest audible sound modulates the air pressure by around 10-6 Pascal (Pa). The loudest (pain inflicting) audible sound does it by 102 Pa. • Because of this wide range it is convenient to measure sound amplitude on a logarithmic scale in Decibel [dB]. -

Appendix 4.10-A: Basics of Noise and Vibration
APPENDIX 4.10-A: BASICS OF NOISE AND VIBRATION A. Noise and Vibration Terminology 1. Noise Noise is unwanted sound. Several noise measurement scales are used to describe noise in a specific location. A decibel (dB) is a unit of measurement that indicates the relative amplitude of a sound. The zero on the decibel scale is based on the lowest sound pressure that the healthy, unimpaired human ear can detect under controlled conditions. Sound levels in decibels are calculated on a logarithmic basis using the ratio of the assumed or measured sound pressure divided by a standardized, reference pressure (for sound, the reference pressure is 20 µPascals). Each 10 dB increase in sound level is perceived as an approximate doubling of loudness over a fairly wide range of amplitudes. There are several methods of characterizing sound. The A-scale is a filter system that closely approximates the way the human ear perceives sound at different frequencies. Noise levels using A-weighted measurements are denoted with the abbreviation of “dB(A)” or “dBA.” The A-weighting filter system is very commonly used in the measurement and reporting of community noise, as well as in nearly all regulations and ordinances. All sound levels in this report are A-weighted, unless noted otherwise. Because sound levels can vary markedly over a short period of time, a method for describing either the average character of the sound or the statistical behavior of the variations must be utilized. Most commonly, environmental sounds are described in terms of an average level that has the same acoustical energy as the summation of all the time-varying events. -

Sound Level Measurement and Analysis Sound Pressure and Sound Pressure Level
www.dewesoft.com - Copyright © 2000 - 2021 Dewesoft d.o.o., all rights reserved. Sound Level Measurement and Analysis Sound Pressure and Sound Pressure Level The sound is a mechanical wave which is an oscillation of pressure transmitted through a medium (like air or water), composed of frequencies within the hearing range. The human ear covers a range of around 20 to 20 000 Hz, depending on age. Frequencies below we call sub-sonic, frequencies above ultra- sonic. Sound needs a medium to distribute and the speed of sound depends on the media: in air/gases: 343 m/s (1230 km/h) in water: 1482 m/s (5335 km/h) in steel: 5960 m/s (21460 km/h) If an air particle is displaced from its original position, elastic forces of the air tend to restore it to its original position. Because of the inertia of the particle, it overshoots the resting position, bringing into play elastic forces in the opposite direction, and so on. To understand the proportions, we have to know that we are surrounded by constant atmospheric pressure while our ear only picks up very small pressure changes on top of that. The atmospheric (constant) pressure depending on height above sea level is 1013,25 hPa = 101325 Pa = 1013,25 mbar = 1,01325 bar. So, a sound pressure change of 1 Pa RMS (equals 94 dB) would only change the overall pressure between 101323.6 and 101326.4 Pa. Sound cannot propagate without a medium - it propagates through compressible media such as air, water and solids as longitudinal waves and also as transverse waves in solids.