Physics Handbook 2020-21
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PHYSICS Glossary
Glossary High School Level PHYSICS Glossary English/Haitian TRANSLATION OF PHYSICS TERMS BASED ON THE COURSEWORK FOR REGENTS EXAMINATIONS IN PHYSICS WORD-FOR-WORD GLOSSARIES ARE USED FOR INSTRUCTION AND TESTING ACCOMMODATIONS FOR ELL/LEP STUDENTS THE STATE EDUCATION DEPARTMENT / THE UNIVERSITY OF THE STATE OF NEW YORK, ALBANY, NY 12234 NYS Language RBERN | English - Haitian PHYSICS Glossary | 2016 1 This Glossary belongs to (Student’s Name) High School / Class / Year __________________________________________________________ __________________________________________________________ __________________________________________________________ NYS Language RBERN | English - Haitian PHYSICS Glossary | 2016 2 Physics Glossary High School Level English / Haitian English Haitian A A aberration aberasyon ability kapasite absence absans absolute scale echèl absoli absolute zero zewo absoli absorption absòpsyon absorption spectrum espèk absòpsyon accelerate akselere acceleration akselerasyon acceleration of gravity akselerasyon pezantè accentuate aksantye, mete aksan sou accompany akonpaye accomplish akonpli, reyalize accordance akòdans, konkòdans account jistifye, eksplike accumulate akimile accuracy egzatitid accurate egzat, presi, fidèl achieve akonpli, reyalize acoustics akoustik action aksyon activity aktivite actual reyèl, vre addition adisyon adhesive adezif adjacent adjasan advantage avantaj NYS Language RBERN | English - Haitian PHYSICS Glossary | 2016 3 English Haitian aerodynamics ayewodinamik air pollution polisyon lè air resistance -

Physics Courses Short Descriptions
Physics Courses Short Descriptions College of Sciences -Al Zulfi Department of Physics Physics Program Physics Courses Short Description 1Page Physics Courses Short Descriptions Physics Courses Short Descriptions College of Sciences -Al Zulfi Department of Physics Physics Program Contents PHYS201: General Physics I .......................................................................................... 4 PHYS202: General Physics II......................................................................................... 4 PHYS211: Classical Mechanics ...................................................................................... 5 PHYS231: Vibrations and Waves ................................................................................... 5 PHYS241: Thermodynamics .......................................................................................... 6 PHYS291: Thermal physics lab. ..................................................................................... 6 PHYS303: Mathematical Physics I ................................................................................. 6 PHYS221: Electromagnetism I ....................................................................................... 6 PHYS332: Optics ......................................................................................................... 7 PHYS351: Modern Physics ............................................................................................ 7 PHYS304: Mathematical Physics................................................................................... -

Physics 103/105 Lab Manual
Princeton University Physics Department Physics 103/105 Lab Manual Fall 2009 Physics 103/105 labs start Monday September 21, 2008. It's important that you go to the lab section that you signed up for. We will be expecting you! You should have a lab book and a scientific calculator when you come to your first lab. (See details in the Orientation section following.) Each week, before you come to lab: Read the procedure for that week's lab, and any additional reading required. The Prelab problems are optional, but please work them if it appears that they will be of help to you. Also, for the first week: Read the “Orientation to Physics 103/105 Lab” and “Error Analysis – Guidance and Reference Text” sections of this packet, and the assigned sections in Taylor. Physics 103 Course Director: Jim Olsen, [email protected], 258-4910 Physics 105 Course Director: David Huse, [email protected], 258-4407 Physics 103/105 Lab Manager: Kirk McDonald, [email protected], 258-6608 Technical Support: Jim Ewart, [email protected], 258-4381 Physics 103/105 Course Associate: Karen Kelly, [email protected], 258-54418 PHYSICS 103/105 LAB MANUAL Table of Contents Title Page Lab Schedule iii Orientation to Physics 103/105 lab v Error Analysis – Guidance and Reference Text xi Lab #1: Encountering the Equipment; Bouncing Balls, etc. 1 Lab #2: Describing Measurement Variability 17 Lab #3: Free Fall, Terminal Velocity 31 Lab #4: Collisions and Conservations 37 Lab #5: Inclined Planes and Energy Conservation 45 Lab #6: Two Nice Experiments in Rotational Motion 51 Lab #7: Fluids 57 Lab #8: Coupled Pendulums and Normal Modes 65 Lab #9: Precision Measurement of g 75 Lab #10: The Speed of Sound and Specific Heats of Gases 87 Appendix A: Data Analysis with Excel 97 ii Princeton University Physics 103/105 Lab, Fall 2008 Physics Department LAB SCHEDULE Remember: Always read the writeup and any reference material before coming to lab. -
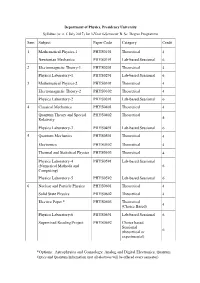
Sem Subject Paper Code Category Credit 1 Mathematical Physics-1
Department of Physics, Presidency University Syllabus (w. e. f. July 2017) for 3-Year 6-Semester B. Sc. Degree Programme Sem Subject Paper Code Category Credit 1 Mathematical Physics-1 PHYS0101 Theoretical 4 Newtonian Mechanics PHYS0191 Lab-based Sessional 6 2 Electromagnetic Theory-1 PHYS0201 Theoretical 4 Physics Laboratory-1 PHYS0291 Lab-based Sessional 6 3 Mathematical Physics-2 PHYS0301 Theoretical 4 Electromagnetic Theory-2 PHYS0302 Theoretical 4 Physics Laboratory-2 PHYS0391 Lab-based Sessional 6 4 Classical Mechanics PHYS0401 Theoretical 4 Quantum Theory and Special PHYS0402 Theoretical 4 Relativity Physics Laboratory-3 PHYS0491 Lab-based Sessional 6 5 Quantum Mechanics PHYS0501 Theoretical 4 Electronics PHYS0502 Theoretical 4 Thermal and Statistical Physics PHYS0503 Theoretical 4 Physics Laboratory-4 PHYS0591 Lab-based Sessional (Numerical Methods and 6 Computing) Physics Laboratory-5 PHYS0592 Lab-based Sessional 6 6 Nuclear and Particle Physics PHYS0601 Theoretical 4 Solid State Physics PHYS0602 Theoretical 4 Elective Paper * PHYS0603 Theoretical 4 (Choice Based) Physics Laboratory-6 PHYS0691 Lab-based Sessional 6 Supervised Reading/Project PHYS0692 Choice based Sessional (theoretical or 6 experimental) *Options: Astrophysics and Cosmology, Analog and Digital Electronics, Quantum Optics and Quantum Information (not all electives will be offered every semester) Semester-1 PHYS0101: Mathematical Physics-1 [50 Lectures] Vector Algebra, Matrices and Vector Spaces [7] Fundamental operations: Scalars, vectors and equality, base vectors, Basic operations in vector space, scalar triple product, vector triple product, differentiation of vectors. Cartesian reference frames. Matrices: Functions of matrices transpose of matrices, the complex and Hermitian conjugates of a matrix, inverse of matrix. Special types of square matrix: Diagonal, triangular, symmetric, orthogonal, Hermitian, unitary. -

영어 우리말 a Balloon Satellite 기구 위성 a Posteriori Probability 후시
영어 우리말 a balloon satellite 기구 위성 a posteriori probability 후시(적) 확률, 사후 확률 a priori 선험- a priori distribution 선험 분포 a priori probability 선험 확률 Abbe prism 아베 프리즘, 아베 각기둥 Abbe's refractometer 아베 굴절계, 아베 꺾임 재개 Abelian group 아벨군, 아벨 무리, 가환군 aberration (1)수차 (2)광행차 abnormal birefringence 비정상 복굴절, 비정상 겹꺾임 abnormal glow discharge 비정상 글로 방전 abnormal liquid 비정상 액체 abnormal reflection 비정상 반사, 비정상 되비침 abnormal scattering 비정상 산란, 비정상 흩뜨림 A-bomb 원자 폭탄 [= atomic bomb] abrasion 마멸, 벗겨짐 abscissa 가로축, 횡축 absolute 절대- absolute ampere 절대 암페어「단위」 absolute convergence 절대 수렴 absolute counting 절대 수셈 absolute counting method 절대 수셈법 absolute differential calculus (1)절대 미분 (2)절대미분학 absolute electromagnetic unit 절대 전자기 단위 absolute electrometer 절대 전위계 absolute error 절대 오차 absolute galvanometer 절대 검류계 absolute humidity 절대 습도 absolute hygrometer 절대습도계 absolute luminosity 절대 광도 absolute magnetic well 절대 자기 우물 absolute magnitude 절대 크기 absolute measurement 절대 측정 absolute motion 절대 운동 absolute parallax 절대 시차 absolute pressure 절대 압력 absolute refractive index 절대 굴절률, 절대 꺾임률 absolute rest 절대 정지 absolute space 절대 공간 absolute system of units 절대 단위계 absolute temperature 절대 온도 absolute temperature scale 절대 온도 눈금 absolute time 절대 시간 absolute unit 절대 단위 absolute vacuum 절대 진공 absolute value 절대값 absolute viscosity 절대 점(성)도 absolute zero 절대 영도 absolute zero point 절대 영(도)점 absolute zero potential 절대 영퍼텐셜 absolutely convergent series 절대 수렴 급수 absorbance (1)흡수도 (2)흡광도 absorbancy (1)흡수도 (2)흡광도 absorbent (1)흡수제 (2)흡광제 absorber (1)흡수체, 흡수기 (2)흡광체 absorptance 흡수율 absorption (1)흡수 (2)흡광 (3)흡음 -

Pivot Library
Pivot Interactives by Subject Tag Biology • Mitosis in Onion Root Tips • Cell Size and Diffusion • Introduction to Acids and Bases • Environmental Effects on Hatching Brine Shrimp • Osmosis and Diffusion: Concentration, Membranes and Motion • Population Dynamics of Algae • Garden of Splendor • Transpiration Rates • Osmosis and Water Potential in Vegetables and Fruits • Plant Genetics – Single Trait Crosses • Animal Behavior: Brine Shrimp and Light • Exploring Respiration Rates • Introduction to Cellular Respiration • Introduction to Cellular Respiration – In Class Collaboration • Introduction to Photosynthesis • Colored Lights and Photosynthesis • Catalase Activity Investigation • Natural Selection of Yeas in Ethanol Environments • Heat of Combustion of Carbon Chains and Food • Gene Regulation: Yeast and Galactose • Comparing Human Respiration Before and After Running • Fruit Fly Genetics – Sex-linked Genes • Introduction to Fermentation • Measuring the Output of the Sun • TorQue and the Human Knee Joint Chemistry • Properties of Ionic and Covalent Bonded Substances • Solubility Rules • Masses of Gases • Stoichiometry Practice: Magnesium and Hydrochloric Acid Reaction • Introduction to Acids and Bases • Introduction to Reversible Reactions • Introduction to Acid-Base Titrations • Enthalpy of Reaction: Acids and Bases with Limiting Reagents • Will it Float? (Calculating the Density of Gases) • Penny Isotopes: Determine the Percent Composition of Copper and Zinc Pennies • Introduction to Measurement • Buoyancy Problem • Temperature During -

DOCUMENT RESUME AUTHOR Gottlieb, Herbert H. Physics Lab Experiments and Correlated Computer Aids. REPORT NO ISBN-0-940850-01-X A
DOCUMENT RESUME EDI 219 228 SE 860 a AUTHOR Gottlieb, Herbert H. TITLE Physics Lab Experiments and Correlated Computer Aids. Teacher Edition. REPORT NO ISBN-0-940850-01-X PUB DATE 81 NOTE 224p. AVAILABLE FROMMetrologic Publications, 143 Harding Ave., Bell Mawr, NJ 08031 $10.50 qer copy,,$6. in clas sets. EDRS PRICE MF01/PC09 Plus Postage. DESCRIPTORS Computer Oriented Programs; High Schools; Laboratory Manuals;.*Physics; *Science'Activitieg; Science Educatibn; *Science Experiments; *Secondary Schaol Science; Teaching Guides ABSTRACT Forty-nine physics experiments are.included in the ' teacher's edition of this ' aboratory rnrvual. Suggestions, are given in margins for preparing apparatus, organizing students, and anticipating difficulties likely,to be encountered. Sample data, graphs, calculations, and sample answers to leading questions are also given for each experiment. it is suggested that data obtained be verified with microcomputers. Subjects of experiments include among others measuring with precision; vector addition of forces; torques; resolution of a force into components; forces caused by weights on an incline, timer calibration; recording motion with strobe photographs; 41 straight-line motion at constant speed; constant acceleration using a water clock; acceleration'of a spinning disc; acceleration using a linear air track;..,pendulum; acceleration of free fall; mass/weight; Newton's second law; trajectories; Newton's third law;conseivation( of energy in a pendulum; energy changes on a tilted air track; simple harmohic motion of a linear air tract; oscillating mass hanging from a spring; mechanical resonance; Boyle's la*;calibrating a mercury thermometer; linear expansion of a solid; calorimetry; thinge of state; waves on a coiled spring and in a:ripple tank; reflection/refraction; diffraction/interface; images and converging/diverging lenses; standing waves; electric fields and electron charge; Ohm's Law; seriesAparallel circuits; Magnetic ,fields; electron beam deflection;_ and half:71ife. -

Acceleration
Team:___________________ _______________ Acceleration Part I. Uniformly Accelerated Motion: Kinematics & Geometry Acceleration is the rate of change of velocity with respect to time: a ≡ dv/dt. In this experiment, you will study a very important class of motion called uniformly-accelerated motion. Uniform acceleration means that the acceleration is constant − independent of time − and thus the velocity changes at a constant rate. The motion of an object (near the earth’s surface) due to gravity is the classic example of uniformly accelerated motion. If you drop any object, then its velocity will increase by the same amount (9.8 m/s) during each one-second interval of time. Galileo figured out the physics of uniformly-accelerated motion by studying the motion of a bronze ball rolling down a wooden ramp. You will study the motion of a glider coasting down a tilted air track. You will discover the deep connection between kinematic concepts (position, velocity, acceleration) and geometric concepts (curvature, slope, area). A. The Big Four: t , x , v , a The subject of kinematics is concerned with the description of how matter moves through space and time . The four quantities, time t, position x, velocity v, and acceleration a, are the basic descriptors of any kind of motion of a particle moving in one spatial dimension. They are the “stars of the kinema”. The variables describing space (x) and time (t) are the fundamental kinematic entities. The other two (v and a) are derived from these spatial and temporal properties via the relations v ≡ dx/dt and a ≡ dv/dt. -

PHYSICS DEPARTMENT November 21, 2016
HARVEY MUDD COLLEGE PHYSICS DEPARTMENT November 21, 2016 LIST OF DEMONSTRATIONS USING THE PIRA SCHEME The PIRA Demonstration Classification Scheme The goal of the PIRA Demonstration Classification Scheme is to create a logically organized and universally inclusive taxonomy giving a unique number to every lecture demonstration. The structure of the classification system is as follows: Example: 1C10.25 – Glider on Air Track 1 Area (mechanics) C Topic (motion in one dimensions) 10 Concept (velocity) .25 Demonstration (Glider on Air Track) PIRA CLASSIFICATION SCHEME Mechanics 1A - Measurement 1C - Motion in One Dimension 1D - Motion in Two Dimensions 1E - Relative Motion 1F - Newton's First Law 1G - Newton's Second Law 1H - Newton's Third Law 1J - Statics of Rigid Bodies 1K - Applications of Newton's Laws 1L - Gravity 1M - Work and Energy 1N - Linear Momentum and Collisions 1Q - Rotational Dynamics 1R - Properties of Matter 1T – Theoretical Physics Fluid Mechanics 2A - Surface Tension 2B - Statics of Fluids 2C - Dynamics of Fluids Oscillations and Waves 3A - Oscillations 3B - Wave Motion 3C - Acoustics 3D - Instruments 3E – Sound Reproduction Thermodynamics 4A - Thermal Properties of Matter 4B - Heat and the First Law 4C - Change of State 4D - Kinetic Theory 4E - Gas Law 4F - Entropy and the Second Law Electricity and Magnetism 5A - Electrostatics 5B - Electric Fields and Potential 5C - Capacitance 5D - Resistance 5E - Electromotive Force and Current 5F - DC Circuits 5G - Magnetic Materials 5H - Magnetic Fields and Forces 5J - Inductance -

Experiments in Physics Physics 1291 General Physics I
Experiments in Physics Physics 1291 General Physics I Lab Columbia University Department of Physics Fall 2019 Contents 1-0 General Instructions 5 1-1 Intro to Labs and Uncertainty 13 1-2 Uncertainty and Error 29 1-3 Velocity, Acceleration, and g 39 1-4 Forces 49 1-5 Projectile Motion and Conservation of Energy 61 1-6 Conservation of Momentum 69 1-7 Torque and Rotational Inertia 81 1-8 Centripetal Force and Angular Momentum Conservation 91 1-9 Waves I: Standing Waves 99 1-10 Waves II: The Oscilloscope and Function Generator 111 1-11 Ideal Gas and Thermal Conductivity 123 Appendices 136 1-A Advanced Error Analysis 139 3 4 Experiment 1-0 General Instructions 1 Purpose of the Laboratory The laboratory experiments described in this manual are an important part of your physics course. Most of the experiments are designed to illustrate important concepts described in the lectures. Whenever possible, the material will have been discussed in lecture before you come to the laboratory. But some of the material, like the first experiment on measurement and errors, is not discussed at length in the lecture. The sections headed Applications and Lab Preparation Exercises, which are in- cluded in some of the manual sections, are not required reading unless your laboratory instructor specifically assigns some part. The Applications are intended to be motiva- tional and so should indicate the importance of the laboratory material in medical and other applications. The Lab Preparation Exercises are designed to help you prepare for the lab. The individual laboratory instructors may require you to prepare answers to these problems. -

Physics 101 Lab Manual
Princeton University Physics 101 Lab Manual (Revised August 1, 2014) m1 Contents 1 Newton’s Laws: Motion in One Dimension 1 2 Motion in Two Dimensions 11 3 The Pendulum 19 4 Collisions in Two Dimensions 25 5 Rotational Motion 33 6 Springs and Simple Harmonic Motion 41 7 Fluids 45 8 Speed of Sound and Specific Heats 51 A Data Analysis with Excel 55 B Estimation of Errors 59 C Standard Deviation of the Mean of g 65 D Polynomial Fits in WPtools 69 3 Lab 1: Newton’s Laws: Motion in One Dimension 1.1 Background In this lab you will study the motion of bodies moving in one dimension. To minimize unwanted forces on the test object, you will use an air track (see Fig. 1.1). The glider floats on a cushion of air above the track, eliminating most of the friction between the glider and the track. The glider can move freely with no horizontal force, or under the influence of a constant horizontal force when attached via a tape to a weight suspended off one end of the air track (see Fig. 1.2). By measuring the time, t, at which the glider passes several positions, x, you can test Newton’s laws and measure g. Figure 1.1: An air track with two photogates. M a g a m Figure 1.2: Glider of mass m on the horizontal air track, connected by a tape to mass M that falls vertically under the influence of gravity. 1 2 Princeton University PHY101 Lab 1 Motion in One Dimension 1.1.1 Newton’s First Law Newton’s first law states that an object will move at constant velocity if no forces are imposed on it. -

2010, Volume 4 Progress in Physics
2010, VOLUME 4 PROGRESS IN PHYSICS “All scientists shall have the right to present their scien- tific research results, in whole or in part, at relevant sci- entific conferences, and to publish the same in printed scientific journals, electronic archives, and any other media.” — Declaration of Academic Freedom, Article 8 ISSN 1555-5534 The Journal on Advanced Studies in Theoretical and Experimental Physics, including Related Themes from Mathematics PROGRESS IN PHYSICS A quarterly issue scientific journal, registered with the Library of Congress (DC, USA). This journal is peer reviewed and included in the ab- stracting and indexing coverage of: Mathematical Reviews and MathSciNet (AMS, USA), DOAJ of Lund University (Sweden), Zentralblatt MATH (Germany), Scientific Commons of the University of St. Gallen (Switzerland), Open-J-Gate (India), Referativnyi Zhurnal VINITI (Russia), etc. To order printed issues of this journal, con- OCTOBER 2010 VOLUME 4 tact the Editors. Electronic version of this journal can be downloaded free of charge: http://www.ptep-online.com CONTENTS Editorial Board Minasyan V. and Samoilov V. Formation of Singlet Fermion Pairs in the Dilute Gas of Dmitri Rabounski, Editor-in-Chief Boson-Fermion Mixture . 3 [email protected] Minasyan V. and Samoilov V. Dispersion of Own Frequency of Ion-Dipole by Super- Florentin Smarandache, Assoc. Editor sonic Transverse Wave in Solid . 10 [email protected] Larissa Borissova, Assoc. Editor Comay E. Predictions of High Energy Experimental Results . 13 [email protected] Smarandache F. Neutrosophic Diagram and Classes of Neutrosophic Paradoxes or to Editorial Team the Outer-Limits of Science . 18 Gunn Quznetsov Smarandache F.