DOCSLIB.ORG

Computational Mechanics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Computational Mechanics 1 Overview 1–1 Chapter 1: OVERVIEW 1–2 TABLE OF CONTENTS Page §1.1. Where this Material Fits 1–3 §1.1.1. Computational Mechanics ............. 1–3 §1.1.2. Statics vs. Dynamics .............. 1–4 §1.1.3. Linear vs. Nonlinear ............... 1–4 §1.1.4. Discretization methods .............. 1–4 §1.1.5.FEMVariants................. 1–5 §1.2. What Does a Finite Element Look Like? 1–5 §1.3. The FEM Analysis Process 1–7 §1.3.1.ThePhysicalFEM............... 1–7 §1.3.2. The Mathematical FEM .............. 1–8 §1.3.3. Synergy of Physical and Mathematical FEM ...... 1–9 §1.4. Interpretations of the Finite Element Method 1–10 §1.4.1.PhysicalInterpretation.............. 1–11 §1.4.2. Mathematical Interpretation ............ 1–11 §1.5. Keeping the Course 1–12 §1.6. *What is Not Covered 1–12 §1.7. *Historical Sketch and Bibliography 1–13 §1.7.1. Who Invented Finite Elements? ........... 1–13 §1.7.2. G1: The Pioneers ............... 1–13 §1.7.3.G2:TheGoldenAge............... 1–14 §1.7.4. G3: Consolidation ............... 1–14 §1.7.5. G4: Back to Basics ............... 1–14 §1.7.6. Recommended Books for Linear FEM ........ 1–15 §1.7.7. Hasta la Vista, Fortran .............. 1–15 §1. References...................... 1–16 §1. Exercises ...................... 1–17 1–2 1–3 §1.1 WHERE THIS MATERIAL FITS This book is an introduction to the analysis of linear elastic structures by the Finite Element Method (FEM). This Chapter presents an overview of where the book fits, and what finite elements are. §1.1. Where this Material Fits The field of Mechanics can be subdivided into three major areas: Theoretical Mechanics Applied (1.1) Computational Theoretical mechanics deals with fundamental laws and principles of mechanics studied for their intrinsic scientific value. Applied mechanics transfers this theoretical knowledge to scientific and engineering applications, especially as regards the construction of mathematical models of physical phenomena. Computational mechanics solves specific problems by simulation through numerical methods implemented on digital computers. Remark 1.1. Paraphrasing an old joke about mathematicians, one may define a computational mechanician as a person who searches for solutions to given problems, an applied mechanician as a person who searches for problems that fit given solutions, and a theoretical mechanician as a person who can prove the existence of problems and solutions. §1.1.1. Computational Mechanics Several branches of computational mechanics can be distinguished according to the physical scale of the focus of attention: Nanomechanics and micromechanics Solids and Structures Computational Mechanics Continuum mechanics Fluids (1.2) Multiphysics Systems Nanomechanics deals with phenomena at the molecular and atomic levels of matter. As such it is closely linked to particle physics and chemistry. Micromechanics looks primarily at the crystallo- graphic and granular levels of matter. Its main technological application is the design and fabrication of materials and microdevices. Continuum mechanics studies bodies at the macroscopic level, using continuum models in which the microstructure is homogenized by phenomenological averages. The two traditional areas of application are solid and fluid mechanics. The former includes structures which, for obvious reasons, are fabricated with solids. Computational solid mechanics takes an applied sciences approach, whereas computational structural mechanics emphasizes technological applications to the analysis and design of structures. Computational fluid mechanics deals with problems that involve the equilibrium and motion of liquid and gases. Well developed subsidiaries are hydrodynamics, aerodynamics, acoustics, atmospheric physics, shock and combustion. 1–3 Chapter 1: OVERVIEW 1–4 Multiphysics is a more recent newcomer. This area is meant to include mechanical systems that transcend the classical boundaries of solid and fluid mechanics, as in interacting fluids and structures. Phase change problems such as ice melting and metal solidification fit into this category, as do the interaction of control, mechanical and electromagnetic systems. Finally, system identifies mechanical objects, whether natural or artificial, that perform a distin- guishable function. Examples of man-made systems are airplanes, buildings, bridges, engines, cars, microchips, radio telescopes, robots, roller skates and garden sprinklers. Biological systems, such as a whale, amoeba, inner ear, or pine tree are included if studied from the viewpoint of biomechanics. Ecological, astronomical and cosmological entities also form systems.1 In the progression of (1.2) the system is the most general concept. A system is studied by decompo- sition: its behavior is that of its components plus the interaction between components. Components are broken down into subcomponents and so on. As this hierarchical breakdown process continues, individual components become simple enough to be treated by individual disciplines, but component interactions get more complex. Consequently there is a tradeoff art in deciding where to stop.2 §1.1.2. Statics vs. Dynamics Continuum mechanics problems may be subdivided according to whether inertial effects are taken into account or not: Statics Continuum mechanics (1.3) Dynamics In dynamics actual time dependence must be explicitly considered, because the calculation of inertial (and/or damping) forces requires derivatives respect to actual time to be taken. Problems in statics may also be time dependent but with inertial forces ignored or neglected. Accord- ingly static problems may be classed into strictly static and quasi-static. For the former time need not be considered explicitly; any historical time-like response-ordering parameter, if one is needed, will do. In quasi-static problems such as foundation settlement, metal creep, rate-dependent plasticity or fatigue cycling, a realistic measure of time is required but inertial forces are still neglected. §1.1.3. Linear vs. Nonlinear A classification of static problems that is particularly relevant to this book is Linear Statics (1.4) Nonlinear Linear static analysis deals with static problems in which the response is linear in the cause-and- effect sense. For example: if the applied forces are doubled, the displacements and internal stresses also double. Problems outside this domain are classified as nonlinear. 1 Except that their function may not be clear to us. “The usual approach of science of constructing a mathematical model cannot answer the questions of why there should be a universe for the model to describe. Why does the universe go to all the bother of existing? Is the unified theory so compelling that it brings about its own existence? Or does it need a creator, and, if so, does he have any other effect on the universe? And who created him?” (Stephen Hawking). 2 Thus in breaking down a car engine for engineering analysis, say, the decomposition does not usually proceed beyond the components you can buy at a parts shop. 1–4 1–5 §1.2 WHAT DOES A FINITE ELEMENT LOOK LIKE? §1.1.4. Discretization methods A final classification of CSM static analysis is based on the discretization method by which the continuum mathematical model is discretized in space, i.e., converted to a discrete model with a finite number of degrees of freedom: Finite Element (FEM) Boundary Element (BEM) Finite Difference (FDM) Spatial discretization method (1.5) Finite Volume (FVM) Spectral Meshfree In CSM linear problems finite element methods currently dominate the scene as regards space discretization.3 Boundary element methods post a strong second choice in specific application areas. For nonlinear problems the dominance of finite element methods is overwhelming. Space finite difference methods in solid and structural mechanics have virtually disappeared from practical use. This statement is not true, however, for fluid mechanics, where finite difference discretization methods are still important. Finite-volume methods, which directly address the dis- cretization of conservation laws, are important in difficult problems of fluid mechanics, for example high-Re gas dynamics. Spectral methods are based on transforms that map space and/or time dimensions to spaces (for example, the frequency domain) where the problem is easier to solve. A recent newcomer to the scene are the meshfree methods. These combine techniques and tools of finite element methods such as variational formulation and interpolation, with finite difference features such as non-local support. §1.1.5. FEM Variants The term Finite Element Method actually identifies a broad spectrum of techniques that share com- mon features outlined in §1.3 and §1.4. Two subclassifications that fit well applications to structural mechanics are4 Displacement Stiffness Equilibrium FEM Formulation FEM Solution Flexibility (1.6) Mixed Mixed (a.k.a. Combined) Hybrid Using the foregoing classification, we can state the topic of this book more precisely: the computa- tional analysis of linear static structural problems by the Finite Element Method. Of the variants listed in (1.6), emphasis is placed on the displacement formulation and stiffness solution. This combination is called the Direct Stiffness Method or DSM. 3 There are finite element discretizations in time, but they are not so widely used as finite differences. 4 The distinction between these subclasses require advanced technical concepts, which cannot be covered in an introductory treatment such as this book. 1–5 Chapter 1: OVERVIEW 1–6 (a) (b) 3 (c) (d) 4 2 4 r 2r sin(π/n) d 5 1 5 i j 2π/n r 6 8 7 Figure 1.1. The “find π” problem treated with FEM concepts: (a) continuum object, (b) a discrete approximation by inscribed regular polygons, (c) disconnected element, (d) generic element. §1.2. What Does a Finite Element Look Like? The subject of this book is FEM. But what is a finite element? The concept will be partly illustrated through a truly ancient problem: find the perimeter L of a circle of diameter d. Since L = π d,this is equivalent to obtaining a numerical value for π. Draw a circle of radius r and diameter d = 2r as in Figure 1.1(a). Inscribe a regular polygon of n sides, where n = 8 in Figure 1.1(b).
Load more

Recommended publications
  • Africa Centre of Excellence on Technology Enhanced Learning (ACETEL)
    CIT 215: INTRODUCTION TO PROGRAMMING LANGUAGE Africa Centre of Excellence on Technology Enhanced Learning (ACETEL) Course Guide 1 NATIONAL OPEN UNIVERSITY OF NIGERIA FACULTY OF SCIENCE COURSE CODE: CIT 215 COURSE TITLE: INTRODUCTION TO PROGRAMMING LANGUAGE 2 Introduction CIT 215 Introduction to Programming Languages is a three [3] credit unit course of twenty units. It deals with Introduction to Programming languages. Programming languages are not very different from spoken languages. Learning any language requires an understanding of the building blocks and the grammar that govern the construction of statements in that language. This book will serve as an introduction to programming languages, taking you through the history of programming languages. We will also learn about the various universal properties of all programming languages and identify distinct design features of each programming language. By the end of this book, you will have a deeper understanding of what a programming language is and the ability to recognize the properties of programming languages. You will also take overview of some programming languages such as to Basic, Fortran, Pascal, C++ , HTML and Visual Basic. Module 1 provides a foundation for the course. In this module we introduce the art of computer programming; explained computer programming languages, and introductory theory of algorithms. Also covered in the module are Flowcharting Techniques and structured programming Module 2: In this module, we provide introductions to the rudiments of BASIC and FORTRAN programming language. In this module we introduce BASIC Programming; explained more programming statements in BASIC, and introduce you to FORTRAN Language. Also covered in the module are FORTRAN Keywords and Library Functions.
    [Show full text]
  • 1 Portraits Leonhard Euler Daniel Bernoulli Johann-Heinrich Lambert
    Portraits Leonhard Euler Daniel Bernoulli Johann-Heinrich Lambert Compiled and translated by Oscar Sheynin Berlin, 2010 Copyright Sheynin 2010 www.sheynin.de ISBN 3-938417-01-3 1 Contents Foreword I. Nicolaus Fuss, Eulogy on Leonhard Euler, 1786. Translated from German II. M. J. A. N. Condorcet, Eulogy on Euler, 1786. Translated from French III. Daniel Bernoulli, Autobiography. Translated from Russian; Latin original received in Petersburg in 1776 IV. M. J. A. N. Condorcet, Eulogy on [Daniel] Bernoulli, 1785. In French. Translated by Daniel II Bernoulli in German, 1787. This translation considers both versions V. R. Wolf, Daniel Bernoulli from Basel, 1700 – 1782, 1860. Translated from German VI. Gleb K. Michajlov, The Life and Work of Daniel Bernoullli, 2005. Translated from German VII. Daniel Bernoulli, List of Contributions, 2002 VIII. J. H. S. Formey, Eulogy on Lambert, 1780. Translated from French IX. R. Wolf, Joh. Heinrich Lambert from Mühlhausen, 1728 – 1777, 1860. Translated from German X. J.-H. Lambert, List of Publications, 1970 XI. Oscar Sheynin, Supplement: Daniel Bernoulli’s Instructions for Meteorological Stations 2 Foreword Along with the main eulogies and biographies [i, ii, iv, v, viii, ix], I have included a recent biography of Daniel Bernoulli [vi], his autobiography [iii], for the first time translated from the Russian translation of the Latin original but regrettably incomplete, and lists of published works by Daniel Bernoulli [vii] and Lambert [x]. The first of these lists is readily available, but there are so many references to the works of these scientists in the main texts, that I had no other reasonable alternative.
    [Show full text]
  • New General Principle of Mechanics and Its Application to General Nonideal Nonholonomic Systems
    New General Principle of Mechanics and Its Application to General Nonideal Nonholonomic Systems Firdaus E. Udwadia1 Abstract: In this paper we develop a general minimum principle of analytical dynamics that is applicable to nonideal constraints. The new principle encompasses Gauss’s Principle of Least Constraint. We use this principle to obtain the general, explicit, equations of motion for holonomically and/or nonholonomically constrained systems with non-ideal constraints. Examples of a nonholonomically constrained system where the constraints are nonideal, and of a system with sliding friction, are presented. DOI: 10.1061/͑ASCE͒0733-9399͑2005͒131:4͑444͒ CE Database subject headings: Constraints; Equations of motion; Mechanical systems; Friction. Introduction ments. Such systems have, to date, been left outside the perview of the Lagrangian framework. As stated by Goldstein ͑1981, p. The motion of complex mechanical systems is often mathemati- 14͒ “This ͓total work done by forces of constraint equal to zero͔ cally modeled by what we call their equations of motion. Several is no longer true if sliding friction is present, and we must exclude formalisms ͓Lagrange’s equations ͑Lagrange 1787͒, Gibbs– such systems from our ͓Lagrangian͔ formulation.” And Pars Appell equations ͑Gibbs 1879, Appell 1899͒, generalized inverse ͑1979͒ in his treatise on analytical dynamics writes, “There are in equations ͑Udwadia and Kalaba 1992͔͒ have been developed for fact systems for which the principle enunciated ͓D’Alembert’s obtaining the equations of motion for such structural and me- principle͔… does not hold. But such systems will not be consid- chanical systems. Though these formalisms do not all afford the ered in this book.” Newtonian approaches are usually used to deal same ease of use in any given practical situation, they are equiva- with the problem of sliding friction ͑Goldstein 1981͒.
    [Show full text]
  • On Stability Problem of a Top Rendiconti Del Seminario Matematico Della Università Di Padova, Tome 68 (1982), P
    RENDICONTI del SEMINARIO MATEMATICO della UNIVERSITÀ DI PADOVA V. V. RUMJANTSEV On stability problem of a top Rendiconti del Seminario Matematico della Università di Padova, tome 68 (1982), p. 119-128 <http://www.numdam.org/item?id=RSMUP_1982__68__119_0> © Rendiconti del Seminario Matematico della Università di Padova, 1982, tous droits réservés. L’accès aux archives de la revue « Rendiconti del Seminario Matematico della Università di Padova » (http://rendiconti.math.unipd.it/) implique l’accord avec les conditions générales d’utilisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte- nir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ On Stability Problem of a Top. V. V. RUMJANTSEV (*) This paper deals with the stability of a heavy gyrostate [1] on a horizontal plane. The gyrostate is considered as a rigid body with a rotor rotating freely (without friction) about an axis invariably con- nected with the body leaning on a plane by a convex surface, i.e. the top in a broad sence of this word. For mechanician the top is a symple and principal object of study [2] attracting investigators’ attention. 1. Let $ql be the fixed coordinate system with the origin in some point of a horizontal plane and vertically up directed axis I with unit vector y; OXIX2Xa is the coordinate system rigidly connected with the body with the origin in centre of mass of gyrostate and axis ~3 coincided with one of its principal central axes of inertia.
    [Show full text]
  • On the Foundations of Analytical Dynamics F.E
    International Journal of Non-Linear Mechanics 37 (2002) 1079–1090 On the foundations of analytical dynamics F.E. Udwadiaa; ∗, R.E. Kalabab aAerospace and Mechanical Engineering, Civil Engineering, Mathematics, and Information and Operations Management, 430K Olin Hall, University of Southern California, Los Angeles, CA 90089-1453, USA bBiomedical Engineering and Economics, University of Southern California, Los Angeles, CA 90089, USA Abstract In this paper, we present the general structure for the explicit equations of motion for general mechanical systems subjected to holonomic and non-holonomic equality constraints. The constraints considered here need not satisfy D’Alembert’s principle, and our derivation is not based on the principle of virtual work. Therefore, the equations obtained here have general applicability. They show that in the presence of such constraints, the constraint force acting on the systemcan always be viewed as madeup of the sumof two components.The explicit formfor each of the two components is provided. The ÿrst of these components is the constraint force that would have existed, were all the constraints ideal; the second is caused by the non-ideal nature of the constraints, and though it needs speciÿcation by the mechanician and depends on the particular situation at hand, this component nonetheless has a speciÿc form. The paper also provides a generalized formof D’Alembert’sprinciple which is then used to obtain the explicit equations of motion for constrained mechanical systems where the constraints may be non-ideal. We show an example where the new general, explicit equations of motion obtained in this paper are used to directly write the equations of motion for describing a non-holonomically constrained system with non-ideal constraints.
    [Show full text]
  • BASIC Programming with Unix Introduction
    LinuxFocus article number 277 http://linuxfocus.org BASIC programming with Unix by John Perr <johnperr(at)Linuxfocus.org> Abstract: About the author: Developing with Linux or another Unix system in BASIC ? Why not ? Linux user since 1994, he is Various free solutions allows us to use the BASIC language to develop one of the French editors of interpreted or compiled applications. LinuxFocus. _________________ _________________ _________________ Translated to English by: Georges Tarbouriech <gt(at)Linuxfocus.org> Introduction Even if it appeared later than other languages on the computing scene, BASIC quickly became widespread on many non Unix systems as a replacement for the scripting languages natively found on Unix. This is probably the main reason why this language is rarely used by Unix people. Unix had a more powerful scripting language from the first day on. Like other scripting languages, BASIC is mostly an interpreted one and uses a rather simple syntax, without data types, apart from a distinction between strings and numbers. Historically, the name of the language comes from its simplicity and from the fact it allows to easily teach programming to students. Unfortunately, the lack of standardization lead to many different versions mostly incompatible with each other. We can even say there are as many versions as interpreters what makes BASIC hardly portable. Despite these drawbacks and many others that the "true programmers" will remind us, BASIC stays an option to be taken into account to quickly develop small programs. This has been especially true for many years because of the Integrated Development Environment found in Windows versions allowing graphical interface design in a few mouse clicks.
    [Show full text]
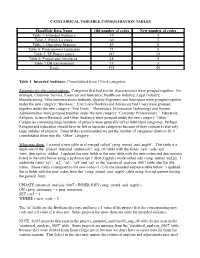
  • Categorical Variable Consolidation Tables
    CATEGORICAL VARIABLE CONSOLIDATION TABLES FlossMole Data Name Old number of codes New number of codes Table 1: Intended Audience 19 5 Table 2: FOSS Licenses 60 7 Table 3: Operating Systems 59 8 Table 4: Programming languages 73 8 Table 5: SF Project topics 243 19 Table 6: Project user interfaces 48 9 Table 7 DB Environment 33 3 Totals 535 59 Table 1: Intended Audience: Consolidated from 19 to 4 categories Rationale for this consolidation: Categories that had similar characteristics were grouped together. For example, Customer Service, Financial and Insurance, Healthcare Industry, Legal Industry, Manufacturing, Telecommunications Industry, Quality Engineers and Aerospace were grouped together under the new category “Business.” End Users/Desktop and Advanced End Users were grouped together under the new category “End Users.” Developers, Information Technology and System Administrators were grouped together under the new category “Computer Professionals.” Education, Religion, Science/Research and Other Audience were grouped under the new category “Other.” Categories containing large numbers of projects were generally left as individual categories. Perhaps Religion and Education should have be left as separate categories because of they contain a relatively large number of projects. Since Mike recommended we get the number of categories down to 50, I consolidated them into the “Other” category. What was done: I created a new table in sf merged called ‘categ_intend_aud_aug06’. This table is a duplicate of the ‘project_intended_audience01_aug_06’ table with the fields ‘new_code’ and ‘new_description’ added. I updated the new fields in the new table with the new codes and descriptions listed in the table below using a python script I (Bob English) wrote called add_categ_intend_aud.py.
    [Show full text]
  • Verification and Validation in Computational Fluid Dynamics1
    SAND2002 - 0529 Unlimited Release Printed March 2002 Verification and Validation in Computational Fluid Dynamics1 William L. Oberkampf Validation and Uncertainty Estimation Department Timothy G. Trucano Optimization and Uncertainty Estimation Department Sandia National Laboratories P. O. Box 5800 Albuquerque, New Mexico 87185 Abstract Verification and validation (V&V) are the primary means to assess accuracy and reliability in computational simulations. This paper presents an extensive review of the literature in V&V in computational fluid dynamics (CFD), discusses methods and procedures for assessing V&V, and develops a number of extensions to existing ideas. The review of the development of V&V terminology and methodology points out the contributions from members of the operations research, statistics, and CFD communities. Fundamental issues in V&V are addressed, such as code verification versus solution verification, model validation versus solution validation, the distinction between error and uncertainty, conceptual sources of error and uncertainty, and the relationship between validation and prediction. The fundamental strategy of verification is the identification and quantification of errors in the computational model and its solution. In verification activities, the accuracy of a computational solution is primarily measured relative to two types of highly accurate solutions: analytical solutions and highly accurate numerical solutions. Methods for determining the accuracy of numerical solutions are presented and the importance of software testing during verification activities is emphasized. The fundamental strategy of 1Accepted for publication in the review journal Progress in Aerospace Sciences. 3 validation is to assess how accurately the computational results compare with the experimental data, with quantified error and uncertainty estimates for both.
    [Show full text]
  • Recent Advances in Multi-Body Dynamics and Nonlinear Control
    Recent Advances in Multi-body Dynamics and Nonlinear Control Recent Advances in Multi-body Firdaus E. Udwadia Dynamics and Nonlinear Control Aerospace and Mechanical Engineering This paper presents some recent advances in the dynamics and control of constrained Civil Engineering,, Mathematics multi-body systems. The constraints considered need not satisfy D’Alembert’s principle Systems Architecture Engineering and therefore the results are of general applicability. They show that in the presence of and Information and Operations Management constraints, the constraint force acting on the multi-body system can always be viewed as University of Southern California, Los Angeles made up of the sum of two components whose explicit form is provided. The first of these CA 90089-1453 components consists of the constraint force that would have existed were all the [email protected] constraints ideal; the second is caused by the non-ideal nature of the constraints, and though it needs specification by the mechanician who is modeling the specific system at hand, it nonetheless has a specific form. The general equations of motion obtained herein provide new insights into the simplicity with which Nature seems to operate. They are shown to provide new and exact methods for the tracking control of highly nonlinear mechanical and structural systems without recourse to the usual and approximate methods of linearization that are commonly in use. Keywords : Constrained motion, multi-body dynamics, explicit equations of motion, exact tracking control of nonlinear systems In this paper we extend these results along two directions. First, Introduction we extend D’Alembert’s Principle to include constraints that may be, in general, non-ideal so that the forces of constraint may The general problem of obtaining the equations of motion of a therefore do positive, negative, or zero work under virtual constrained discrete mechanical system is one of the central issues displacements at any given instant of time during the motion of the in multi-body dynamics.
    [Show full text]
  • Explicit Equations of Motion for Constrained
    Explicit equations of motion for constrained mechanical systems with singular mass matrices and applications to multi-body dynamics Firdaus Udwadia, Phailaung Phohomsiri To cite this version: Firdaus Udwadia, Phailaung Phohomsiri. Explicit equations of motion for constrained mechanical systems with singular mass matrices and applications to multi-body dynamics. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, Royal Society, The, 2006, 462 (2071), pp.2097 - 2117. 10.1098/rspa.2006.1662. hal-01395968 HAL Id: hal-01395968 https://hal.archives-ouvertes.fr/hal-01395968 Submitted on 13 Nov 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Distributed under a Creative Commons Attribution| 4.0 International License Explicit equations of motion for constrained mechanical systems with singular mass matrices and applications to multi-body dynamics 1 2 FIRDAUS E. UDWADIA AND PHAILAUNG PHOHOMSIRI 1Civil Engineering, Aerospace and Mechanical Engineering, Mathematics, and Information and Operations Management, and 2Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA We present the new, general, explicit form of the equations of motion for constrained mechanical systems applicable to systems with singular mass matrices. The systems may have holonomic and/or non holonomic constraints, which may or may not satisfy D’Alembert’s principle at each instant of time.
    [Show full text]
  • DEALING with DATA EDITOR’S NOTE Does Your Program Smell Passive Authentication for ASP.NET with WIF Like Bacon? Michele Leroux Bustamante
    THE MICROSOFT JOURNAL FOR DEVELOPERS AUGUST 2010 VOL 25 NO 8 COLUMNS DEALING WITH DATA EDITOR’S NOTE Does Your Program Smell Passive Authentication for ASP.NET with WIF Like Bacon? Michele Leroux Bustamante . 20 Keith Ward page 4 CUTTING EDGE Tips for Migrating Your Applications to the Cloud Don’t Worry, Be Lazy George Huey and Wade Wegner . 36 Dino Esposito page 6 Creating Synchronization Providers DATA POINTS Deny Table Access to the with the Sync Framework Entity Framework Without Joydip Kanjilal . 46 Causing a Mutiny Julie Lerman page 14 Building an AtomPub Server Using WCF Data Services TEST RUN Chris Sells . 54 Fault Injection Testing with TestApi James McCaffrey page 84 Tuning Your Database Calls THE WORKING PROGRAMMER with Tier Interaction Profi ling Inside SQLite Mark Friedman . 62 Ted Neward page 88 UI FRONTIERS Building Distributed Apps with NHibernate Multi-Touch Manipulation Events in WPF and Rhino Service Bus, Part 2 Charles Petzold page 92 Oren Eini . 72 DON’T GET ME STARTED Windows Phone and the Cloud: an Introduction Mars and Venus David Platt page 96 Ramon Arjona . 78 Untitled-5 2 3/5/10 10:16 AM Sure, Visual Studio 2010 has a lot of great functionality— we’re excited that it’s only making our User Interface components even better! We’re here to help you go beyond what Visual Studio 2010 gives you so you can create Killer Apps quickly, easily and without breaking a sweat! Go to infragistics.com/beyondthebox today to expand your toolbox with the fastest, best-performing and most powerful UI controls available.
    [Show full text]
  • Catalogue 176
    C A T A L O G U E – 1 7 6 JEFF WEBER RARE BOOKS Catalogue 176 Revolutions in Science THE CURRENT catalogue continues the alphabet started with cat. #174. Lots of new books are being offered here, including books on astronomy, mathematics, and related fields. While there are many inexpensive books offered there are also a few special pieces, highlighted with the extraordinary LUBIENIECKI, this copy being entirely handcolored in a contemporary hand. Among the books are the mathematic libraries of Dr. Harold Levine of Stanford University and Father Barnabas Hughes of the Franciscan order in California. Additional material is offered from the libraries of David Lindberg and L. Pearce Williams. Normally I highlight the books being offered, but today’s bookselling world is changing rapidly. Many books are only sold on-line and thus many retailers have become abscent from city streets. If they stay in the trade, they deal on-line. I have come from a tradition of old style bookselling and hope to continue binging fine books available at reasonable prices as I have in the past. I have been blessed with being able to represent many collections over the years. No one could predict where we are all now today. What is your view of today’s book world? How can I serve you better? Let me know. www.WeberRareBooks.com On the site are more than 10,000 antiquarian books in the fields of science, medicine, Americana, classics, books on books and fore-edge paintings. The books in current catalogues are not listed on-line until mail-order clients have priority.
    [Show full text]