Defining and Model Checking Abstractions of Complex Railway
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Dccconcepts “Modelling Advice” Publication
A DCCconcepts “Modelling advice” publication DCC Advice #11 Page 1 Wiring Point-work & Special track conditions for DC or DCC Wiring the track… In plain English, with diagrams! If we had a $ or £ or € for every time we’ve been asked how to wire track and point-work, we’d be writing this on a beach somewhere while sipping a cold beer! A great layout needs good trackwork, so first - a word about trackwork and getting good performance. Choose carefully! DO think about making your own turnouts if you have even moderate skills. It is not as hard as you think, needs only basic skills and tools... and we do our best to make it easy with our top quality gauges, trackwork frets and templates. PLUS we will soon provide a detailed “How to make track” tutorial too. Interested? Then call or email us and we will do our best to help you. No matter what scale you will model in, DO NOT even consider using insulated frogs! Yes, lazy retailers who do not understand what they sell - and modellers who have never done a proper job of laying track so it runs well may well recommend it to you… but do NOT be tempted. No matter which brand makes the turnouts, if you use insulated frogs, you WILL have small locos stalling or also suffer from wider wheels bridging the frog tip and creating momentary shorts that are hard to fix and really are a source of constant frustration. Use more realistic rail sizes please: Usually this will be code 55 in N, or Code 75 and 83 in OO or HO Scale. -

Appendix J Haddington Branch Line Survey
Appendix J Haddington Branch Line Survey AllanRail East Lothian Access STAG Physical feasibility of re-opening the Haddington Rail Branch Line Background The reopening of the Haddington Railway branch line from the East Coast Main Line (ECML) at Longniddry to Haddington is one of the options that are required to be considered in the East Lothian Access STAG. This initial report informs the appraisal work of the feasibility of re-opening the railway, some of the issues and problems that would need to be resolved, choices that are available and suggests an order of magnitude cost. Because the rest of the railway is electrified it is assumed that the Haddington branch will also be equipped with standard 25Kv overhead electrification equipment. The report is based on a physical site walk-over on 21 February 2019, carried out by David Prescott of AllanRail who has considerable experience in the initial development of re-opened railways in Scotland including walk-overs on the Stirling – Alloa – Kincardine, Airdrie- Bathgate and Borders Railway routes in the inception and pre-construction stages. This is not an engineering assessment, but an initial view based on observation and experience. The route is considered in the Longniddry to Haddington direction and the report is broken down into key route sections. Connecting to the ECML The ideal connection to the main line has several desirable operating and engineering requirements: · It should be on the Edinburgh side of Longniddry to minimise the occupation of the ECML; · It should provide as -
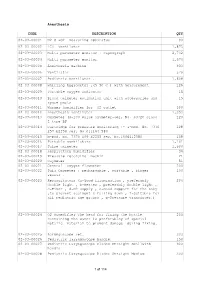
Anesthesia CODE DESCRIPTION QTY 02-03-00001 N2 O +O2
Anesthesia CODE DESCRIPTION QTY 02-03-00001 N2 O +O2 measuring apparatus 90 02-03-00002 ICU Ventilator 1,875 02-03-00003 Multi parameter monitor + capnograph 2,742 02-03-00004 Multi parameter monitor 1,674 02-03-00005 Anesthesia machine 933 02-03-00006 Ventilator 579 02-03-00007 Pediatric ventilator . 1,608 02-03-00008 Whirling hygrometer ,(5-50 C ) with measurement 129 ruler . 02-03-00009 Portable oxygen indicator 15 02-03-00010 Blood oximeter estimation unit with accessories and 15 spare parts 02-03-00011 Warmer humidifier for O2 outlet 300 02-03-00012 Anesthesia Ventilator 1,353 02-03-00013 Oxymeter (S-100 pulse oxymeter-ser, No. S0720 class 120 I type BF 02-03-00014 Cartridge for pressure monitoring :- a-mod. No. 7370 108 257 E2258 ser, No.011164 580 02-03-00015 b-mod. No. 7370 109 E2255 ser, No.1006412580 108 02-03-00016 Portable ventilators 1,101 02-03-00017 Pulse oximeter 1,500 02-03-00018 Respiratory humidifier 36 02-03-00019 Pressure recording machin 21 02-03-00020 Oxymeter 51 02-03-00021 Central oxygen flowmeter 200 02-03-00022 Puls Oxymeter : rechargable , portable , finger 100 sensor . 02-03-00023 Resuscitators (a-Good illumination , preferably 204 double light , b-Heater , preferably double light , c-Timer , d-O2 supply , e-Good support for the baby ,to prevent accident & falling down , f-Suitable for all pediatric age groups , g-Pressure transducer.) 02-03-00024 O2 Humedifier The head for fixing the bottle 200 containing the water is preferabley of special metalic material to prevent damage during fixing. -
8. Portishead to Portbury Dock Junction Overview 17 9
Ref: GS2/140569 Version: 1.00 Date: July 2014 Contents 1. Executive Summary 1 2. Introduction 3 3. Business Objective 6 4. Business Case 9 5. Project Scope 11 6. Deliverables 12 7. Options Considered 13 8. Portishead to Portbury Dock Junction Overview 17 9. Engineering Options 19 10. Bathampton Turnback 52 11. Constructability and Access Strategy 53 12. Cost Estimates 56 13. Project Risks and Assumptions 57 14. High level business case appraisal against whole life costings 58 15. Project Schedule 59 16. Capacity/Route Runner Modelling 60 17. Interface with other Projects 61 18. Impact on Existing Customers, Operators and Maintenance Practice 62 19. Consents Strategy 63 20. Environmental Appraisal 64 21. Common Safety Method for Risk Evaluation Assessment (CSM) 65 22. Contracting Strategy 66 23. Concept Design Deliverables 67 24. Conclusion and Recommendations 68 References 70 Formal Acceptance of Selected Option by Client, Funders and Stakeholders 71 GRIP Stage 2 Governance for Railway Investment Projects Ref: GS2/140569 Version: 1.00 Date: July 2014 Appendices A Drawings B Cost Estimate C Qualitative Cost Risk Analysis D Capacity Modelling E Environmental Appraisal F Signalling Appraisal G Photograph Gallery H Track Bed Investigation (Factual, Interpretative and Hazardous Classification) I Visualisations (Galingaleway and Sheepway Gate Farm) J Interdisciplinary Design Certificate K Portishead Station Options Appraisal Report (produced by North Somerset Council) GRIP Stage 2 Governance for Railway Investment Projects Ref: GS2/140569 Version: 1.00 Date: July 2014 Issue Record Issue No Brief History Of Amendment Date of Issue 0.01 First Draft 30 May 2014 0.02 Second Draft updated to include comments 13 June 2014 1.00 Report Issued 18 July 2014 Distribution List Name Organisation Issue No. -

210116 Update Sheet 01 Amendments to UTE.Indd
UPDATE SHEET 01 Understanding Track Engineering APRIL 2016 The following two sheets have been omitted from: This book is an essential introduction to the theory and practice of railway track engineering in the UK. ChapterIt gives the 9 reader Switches the historical perspective & of how Crossings railway track developed and new forms were designed following Section extensive9.2 researchCrossing and practical experience. Design & The book is aimed at people new to the rail industry and also a guide for the more experienced track engineers who need to Manufacturerefresh their knowledge. The PWI is the professional body in the UK and internationally that is solely dedicated to the advancement of the knowledge of railway infrastructure and promoting the sharing of best In the editionspractice worldwide.of: UPDATE SHEET 01 Understanding Track Engineering Understanding Track Engineering first published in 2014, including APRIL 2016 the e-book, reference PWI 20150414. These pages have been formatted to A5 and are to follow page 330. www.thepwi.org WWW.THEPWI.ORG PWI Knowledge Advice Support Education UPDATE SHEET 01 Understanding Track Engineering - APRIL 2016 Page 1 of 2 UPDATE SHEET 01 Understanding Track Engineering - APRIL 2016 Page 2 of 2 vertical S&C is the need to provide twist rails at each leg of the junction, normally one sleeper bed long. Some layouts occur so frequently that they have acquired their own names. Probably the commonest of these is the CROSSOVER, in which two turnouts are laid crossing Fig 9.3 (a) to crossing in adjoining tracks to enable trains to change tracks, as in Figure 9.3(a). -

Report 04/2018
Rail Accident Report Freight train derailment at Lewisham, south- east London 24 January 2017 Report 04/2018 February 2018 This investigation was carried out in accordance with: l the Railway Safety Directive 2004/49/EC; l the Railways and Transport Safety Act 2003; and l the Railways (Accident Investigation and Reporting) Regulations 2005. © Crown copyright 2018 You may re-use this document/publication (not including departmental or agency logos) free of charge in any format or medium. You must re-use it accurately and not in a misleading context. The material must be acknowledged as Crown copyright and you must give the title of the source publication. Where we have identified any third party copyright material you will need to obtain permission from the copyright holders concerned. This document/publication is also available at www.gov.uk/raib. Any enquiries about this publication should be sent to: RAIB Email: [email protected] The Wharf Telephone: 01332 253300 Stores Road Fax: 01332 253301 Derby UK Website: www.gov.uk/raib DE21 4BA This report is published by the Rail Accident Investigation Branch, Department for Transport. Preface Preface The purpose of a Rail Accident Investigation Branch (RAIB) investigation is to improve railway safety by preventing future railway accidents or by mitigating their consequences. It is not the purpose of such an investigation to establish blame or liability. Accordingly, it is inappropriate that RAIB reports should be used to assign fault or blame, or determine liability, since neither the investigation nor the reporting process has been undertaken for that purpose. The RAIB’s findings are based on its own evaluation of the evidence that was available at the time of the investigation and are intended to explain what happened, and why, in a fair and unbiased manner. -

Network Rail Track Engineering Conference
TECHNICAL ARTICLE AS PUBLISHED IN The Journal January 2019 Volume 137 Part 1 If you would like to reproduce this article, please contact: Alison Stansfield MARKETING DIRECTOR Permanent Way Institution [email protected] PLEASE NOTE THE OPINIONS EXPRESSED IN THIS JOURNAL ARE NOT NECESSARILY THOSE OF THE EDITOR OR OF THE INSTITUTION AS A BODY. TECHNICAL NETWORK RAIL TRACK ENGINEERING CONFERENCE IMechE LONDON NOVEMBER 2018 This year’s Network Rail/PWI Track Croydon is not just East Croydon station, but a Engineering Conference took place at the network around Croydon. There is a collection IMechE in Westminster. Delegates were of stations, and eight key junctions that play welcomed by Pablo Forteza, Project Director, crucial roles in “sorting” train services in Engineering & Innovation, IP, Network Rail. and out of London. The present layout has a confused mix between pairing lines by use and PRESENTATION 1 pairing them by direction of traffic. Together with a lack of grade separation at junctions, this switching about wastes time and increases CROYDON the risks of disruption. Improving performance means attacking PROJECT primary delays by improving the assets (design and quality) and maintaining them better. In OVERVIEW addition, secondary delays must be reduced by having better planning rules and reducing PETER FAGG timetable interactions through grade separation SENIOR PROJECT ENGINEER at junctions. Peter Fagg NETWORK RAIL The BMUP (BM Upgrade Plan) involves more trains, more station capacity, grade separation, In a site only 4km from end to end there will Peter gave a detailed presentation about the optimised layouts, more stabling facilities and be approximately 25km of new track, 100 s&c huge project that he and his colleagues are higher line-speeds. -

How Can Forecast Growth and Partners' Aspirations
FINAL / OFFICIAL Continuous Modular Strategic Planning How can forecast growth and partners’ aspirations be accommodated in the Trent Junctions Area? Strategic Question April 2019 OFFICIAL Trent Junctions / FINAL A. Foreword As part of the railway industry’s Continuous Modular Strategic Planning (CMSP) approach adopted for the Long Term Planning Process (LTPP) we are pleased to present the response to the Trent Junctions area Strategic Question. By 2043, there will have been significant investment in the railway in the East Midlands, firstly through the Midlands Rail Hub scheme which will deliver new services between the key cities of the East Midlands, and the High Speed 2 East Midlands Hub station between Derby and Nottingham. As these new services are introduced, they need to be integrated into the wider rail network, providing a punctual, reliable and valuable service to passengers. One of the major challenges to the introduction of new services around the East Midlands is the Trent Junctions area. Partners from across the rail industry and government identified this as a priority for a CMSP Strategic Question because of the large number of capacity and feasibility studies which have looked at this area. Each of these studies has worked with varied train service and infrastructure assumptions. This study takes an holistic view of these studies, combining them to identify specific locations which will be capacity constraints in the future. Since the Midland Railway Company built Trent Junctions in the mid-nineteenth century, the layout of this area has evolved to deliver different services as the different flows across the junctions have changed. -

The Freight Solution to the Castlefield Problem
The Freight Solution to the Castlefield Problem Including The Business Case for a new route and western access to Trafford Park April 2020 (Revised August 2020) Contents Part 1. The Castlefield Problem – Freight’s Great Opportunity .................................................................................... 2 The Problem ............................................................................................................................................................... 2 A more fundamental question ................................................................................................................................... 5 Carrington Park .......................................................................................................................................................... 6 The search for a route to the south ........................................................................................................................... 7 Connecting to the West Coast Main Line .................................................................................................................. 9 Benefits of the proposed interventions ................................................................................................................... 14 Part 2. The Business Case for a Western Route to Trafford Park ................................................................................ 15 Assumptions ............................................................................................................................................................ -

Railway Modelling in CSP||B:The Double Junction Case Study
Electronic Communications of the EASST Volume 53 (2012) Proceedings of the 12th International Workshop on Automated Verification of Critical Systems (AVoCS 2012) Railway modelling in CSPjjB: the double junction case study Faron Moller, Hoang Nga Nguyen, Markus Roggenbach, Steve Schneider and Helen Treharne 15 pages Guest Editors: Gerald Luttgen,¨ Stephan Merz Managing Editors: Tiziana Margaria, Julia Padberg, Gabriele Taentzer ECEASST Home Page: http://www.easst.org/eceasst/ ISSN 1863-2122 ECEASST Railway modelling in CSPjjB: the double junction case study Faron Moller1, Hoang Nga Nguyen1, Markus Roggenbach1, Steve Schneider2 and Helen Treharne2 1 Swansea University, Wales 2 University of Surrey, England Abstract: This paper reports on recent work in verifying railway systems through CSPjjB modelling and analysis. Our motivation is to develop a modelling and ver- ification approach accessible to railway engineers: it is vital that they can validate the models and verification conditions, and — in the case of design errors — obtain comprehendable feedback. In this paper we run through a full production cycle on a real double junction case study, supplied by our industrial partner, who contributed at every stage. As our formalization is, by design, near to their way of thinking, they are comfortable with it and trust it. Without putting much effort on optimization for verification, the scale of the models analyzed is comparable with the work of other groups. Keywords: Railway verification, CSPjjB, modelling and analysis, ProB. 1 Introduction Formal verification of railway control software has been identified as one of the “Grand Chal- lenges” of Computer Science [Jac04]. But in respect of this challenge, a question has been asked by the community: “Where do the axioms come from?” [Fia12]. -

North South Rail Link Feasibility Reassessment Appendices
Photo Source: Katie Manning / Unsplash 164 North South Rail Link Feasibility Reassessment Final Report January 2019 | Preferred Alignment and Construction Technology 9. Appendices Appendices | January 2019 North South Rail Link Feasibility Reassessment Final Report 165 Photo Source: Michael Hicks / Flickr 166 North South Rail Link Feasibility Reassessment Final Report January 2019 | Appendices A. Citations 1 Eighth in the US in 2017, Inrix Global Conges- 8 MassDOT, The Offcial Website of The Mas- 16 Central Transportation Planning Staff, Boston tion Rankings, http://inrix.com/press-releases/ sachusetts Department of Transportation - Rail Region Metropolitan Planning Organization, los-angeles-tops-inrix-global-congestion- & Transit Division, http://www.massdot.state. Memorandum: MBTA Commuter Rail Passenger ranking/; 10th in the US in 2017, TomTom Traffc ma.us/Transit/ Count Results, Dec. 21, 2012. Index, https://www.tomtom.com/en_gb/traffcin- 9 MassDOT, Tracker 2017: MassDOT’s Annual 17 Boston Region Metropolitan Planning Organiza- dex/list?citySize=LARGE&continent=ALL&coun Performance Report, http://www.massdot.state. tion, Long-Range Transportation Plan – Needs try=ALL ma.us/Portals/0/docs/infoCenter/performance- Assessment, www.ctps.org/lrtp_needs 2 Ridership Trends presentation, MassDOT Offce management/Tracker2017.pdf 18 According to Reconnecting America, a national of Performance Management and Innovation, 10 MBTA, The New MBTA, http://old.mbta.com/ nonproft that integrates transportation and February 27, 2017, http://old.mbta.com/upload- about_the_mbta/history/?id=970 community development, “Transit-oriented edfles/About_the_T/Board_Meetings/M.%20 development… is a type of development that %20Ridership%20Trends%20Final%20022717. 11 https://www.mbtafocus40.com/ includes a mixture of housing, offce, retail and/ pdf or other amenities integrated into a walkable 12 MassDOT, MBTA State of the Service: Com- neighborhood and located within a half-mile of 3 Massachusetts Institute of Technology, Data muter Rail, https://d3044s2alrsxog.cloudfront. -

Annual Report 2006 Preface
Annual Report 2006 Preface This is the Rail Accident Investigation Branch’s (RAIB) annual report for the calendar year 006. Section 1 deals with the background to the RAIB and sets out its aims and statutory duties in relation to the types of accidents that it investigates. Section provides details of the RAIB operations during 006. Section 3 looks at the causes of accidents and the related recommendations arising from all investigations concluded in 006, from commencement of the RAIB on 17 October 005 to 31 December 006. Section 4 deals with other Branch activities. Further details on the reporting schedules and accident statistics can be found in annexes D and E. Annexes F and G include glossaries explaining: • abbreviations and acronyms that have been used within the report; and • technical terms, shown in italics when they appear in text. Rail Accident Investigation Branch RAIB Annual Report www.raib.gov.uk 006 RAIB Annual Report 2006 Contents Chief Inspector’s Foreword 4 1. Introduction to the Rail Accident Investigation Branch 6 . Operations 1 3. Analysis of causes and recommendations 14 4. Other Branch activities 16 Annex A List of investigations opened in 005 and completed in 006, and list of investigations opened and completed in 006 18 Annex B Summary of investigations opened in 006 but not completed by 31.1.006 19 Annex C Recommendation Progress Report 23 Annex C Appendix 1 – Statistics: Recommendations made in 006 and status 24 Annex C Appendix – Recommendations made in 006 to end implementer 25 Annex C Appendix 3 – Recommendation